如何利用“數形結合”解決問題

郭雙

“數缺形，少直觀;形缺數，難入微;數形結合百般好，隔離分家萬事休。”這是著名數學家華羅庚先生對數形結合思想的透徹的闡釋。

數學中，數和形是兩個最主要的研究對象，它們相互轉化、相互滲透。數形結合思想，就是在解決問題的過程中，注意把數和形結合起來考察，斟酌問題的具體情形，把圖形性質的問題轉化為數量關系的問題，利用數量關系突破圖形性質的問題;或者把數量關系的問題轉化為圖形性質的問題，利用圖形的性質解決數量關系的問題。利用數與形的相互轉化來解決數學問題，使復雜問題簡單化，抽象問題具體化，化難為易，獲得簡單易行的成功方案。

畫圖，是數學中常用的一種解題策略。小學生年齡小，抽象思維水平不高，而畫圖比較直觀。通過畫圖能夠把一些抽象的數學問題具體化，把一些復雜的問題簡單化，容易找到解決問題的關鍵。所以引導學生采用畫圖的策略，十分適合小學生的思維特點，也是我最常向學生推薦的一種解題策略。下面談談我在教學中采用“數形結合”思想教學的方法。

一、數形結合，激發學習興趣

畫圖能把抽象的東西形象化、生動化，學生更能積極主動接受知識，變“被動學”為“主動學”。

例如，我在教學人教版二年級上冊《有余數的除法》時，在講授“余數”這一知識點時學生很難理解，于是教師便給學生提供小棒，用8根、9根、10根、11根、12根小棒擺正方形，可以擺幾個正方形，還剩幾根？

通過拼擺正方形，學生很容易就得出結論：8根可拼成2個正方形;9根可拼成2個正方形，還剩1根;10根可拼成2個正方形，還剩2根;11根可拼成2個正方形，還剩3根;12根可拼成3個正方形;這里剩下的1根、2根、3根就是“余數”，表示剩余多出來的數。為什么12根小棒擺正方形沒有余數呢？通過圖形也能很容易得知，11根再添1根，那么余數3根與新添的1根剛好又可以擺成一個正方形，所以沒有余數。也可得出結論：余數比除數小。在這個直觀的操作過程中，學生輕易突破難點，也大大激發了學生學習數的興趣，把學生從“被動學”轉變成“主動學”。

二、數形結合，形成良好學習習慣

巴金先生說：“孩子成功教育從好習慣培養開始。”在數學解題的過程中要善于培養“畫圖”的好習慣。“畫圖”能為學生在解決問題中提供清晰的思路和步驟，形成良好的學習習慣。教師不僅要教會孩子怎樣畫圖，而且要讓孩子將“畫圖”形成一種解題習慣。

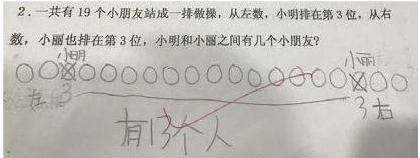
例如，我在教學人教版一年級上冊《11-20各數的認識之解決問題》中遇到這類例題：

首先，我會讓學生畫19個圓圈代表19個小朋友。然后，再找出左邊第三個標注“小明”，右邊第三個標注“小麗”。為了讓學生更清晰的知道小明和小麗不算在內，我讓學生把不算的人數打上“×”。最后，用橫線畫出小明和小麗之間的人數并數出來。

一年級的小朋友對文字的理解有些欠缺，抽象思維水平有限，但通過“畫圖”把文字意思表述出來就一目了然，學生也容易接受。從小埋下一顆善于畫圖解決問題的種子，形成一種良好的學習習慣，對于今后的學習有著莫大的幫助。

三、數形結合，激活學生思維

教育大師蘇霍姆林斯基說過“孩子的智慧在手指上”。 學生在解決數學問題的過程中利用畫圖這個中介輔助理解題目，其實他們在畫圖的過程中就是展示其數學思維過程，閃爍其數學思維火花的過程。學生能把一些看似剪不斷、理還亂的數學難題，“翻譯”成圖表的符號，化繁為簡，使問題變得井然有序。整個過程中，學生把文字轉成圖畫，把圖畫轉成思維，是一個從“外化”到“內化”的過程，是一個發展學生邏輯思維的過程。

記得在教學人教版四年級下冊《雞兔同籠》時，書本出示以下例題：

籠子里有若干只雞和兔，從上面數，有8個頭，從下面數，有26只腳。雞和兔各有幾只？

在數量比較少的情況下，我們可以通過列表格找出答案。但是還不能清晰掌握解題方法，為了讓學生更直觀、簡潔、深刻地理解題意，我采用了畫圖假設。

假設籠子里全部都是雞，那么就有8×2=16只腳，這樣就多出了26-16=10只腳。

一只兔比一只雞多2只腳，也就是10÷2=5只兔。所以籠子里有3只雞和5只兔。

在這個過程中，學生一看圖就可以理解多出來的10只腳是兔子的，一只兔子比雞多2只腳，所以兔子有5只，雞有3只。下次做到類似題目都能先假設全部是雞或者全部是兔的情況，進而進行計算。在教學過程中巧用“畫圖”，能將教學內容化繁為簡，培養學生的抽象思維能力，引導學生在真實鮮明的感性認識中，發展智力因素，可有效地培養他們的抽象思維能力。

四、數形結合，建立數學方法。

教學中利用數形結合，可以啟發學生思考，幫助學生不斷積累數學活動經驗，感受畫圖解題策略價值，提升數學思想方法，同時讓學生根據自己的體驗，逐步領悟，用自己的思維方式構建出數學思想方法的體系。

總之，運用數形結合的思想來解決數學問題，可以將很多抽象的東西趣味化，復雜的東西簡單化，空洞的東西生動化。教師要培養學生學會用數形結合思想來解決數學問題，引導學生在真實鮮明的感性認識中發展智力，體會“畫圖”在數學應用中的魅力。