變式訓練在高中數學解題教學中的應用

江蘇省南京市中華中學 曹曉琰

在傳統的高中數學解題教學過程中，教師為了在有限的課堂時間內讓學生掌握更多的數學解題知識，通常都是以概念作為出發點，運用這些概念來解決數學問題，但是教師卻忽略了這一階段的學生思維能力普遍不高的事實。所以，教師在進行數學解題教學時，不僅要重視數學基本知識的傳授，還要突出解題技巧，應該創新解題訓練的方法，通過變式訓練把理論與實踐相結合，提高學生的解題能力，達到“授人以漁”的目的。

一、變式訓練中變換條件或結論

通過對數學解題問題的分析，我們不難看出，不管多么復雜的數學問題，它們之間都存在著一定的共性，而且這些共性一般都體現在基礎知識的運用上，所以教師在指導學生數學解題時，一定要重視變式訓練，并通過變式訓練把這些基礎知識用活、用好、用通，讓學生在解決實際數學問題的過程中加深對這些基本知識的理解，做到“舉一反三”。

例如，在學習“函數的單調性”時，有這樣一道題：判斷函數y=x2+2，x ∈（0，+∞）的單調性。將該題的條件進行變換，則有以下兩種變式，變式一：判斷函數y=x2+2，x ∈（-∞，0）的單調性；變式二：判斷函數y=x2+2 的單調性。學生通過練習原題與變式一，基本能掌握函數的單調性，再進行變式二的練習時，學生就會發現該函數不是單調函數，若要判斷該函數的單調性，則要分段進行討論，讓學生對函數的定義加以重視，并能有效地培養創造性思維能力。

二、應用變式訓練時變換題設與問題

數學學科作為一門邏輯性非常強的學科，在進行數學解題過程中沒有捷徑可走，學生想要達到良好的學習效果，就必須把基礎知識進行大量的實際應用，從而加深對這些基礎知識的理解和掌握，這就需要通過變式訓練最大程度地把自己的“感性”認識變成“理性”認識，從而不斷完善自己的解題思路。

例如，已知集合P={x ∈N|1 ≤x ≤10}，集合Q={x ∈R|x2+x-6=0}，則P ∩Q 等于（ ）

A.{1，2，3} B.{2，3} C.{1，2} D.{2}

解：集合Q={x ∈R|x2+x-6=0}={-3，2}，所以答案為D。

變式：已知集合P={x ∈N|1 ≤x ≤10}，集合Q={x ∈R|x2-5x+6=0}，則Cp(P ∩Q)等于（ ）

A.{1，2，3} B.{2，3}

C.{1，2} D.{1，4，5，6，7，8，9，10}

解：集合Q={x ∈R|x2-5x+6=0}={3，2}，所以答案為D。

分析：上述變式是將問題改變，條件改變，是在理解基礎問題的前提下，對最后求解的結果改變，再求解P 的補集，多了一個步驟，需要學生在注意運用不等式的時候，理解集合的運用以及補集的運用和求解，屬于低等難度。

三、變式訓練中變換表達方式

高中數學教師在對學生進行解題教學時，可以通過變式訓練的方式對學生的解題能力進行訓練，教師可以對題目中的知識背景不作過多變動，而對表達方面的文字描述內容進行調整。下面將就這一方面的內容進行舉例說明。

例如，已知存在兩個點A（-5，0），B（3，0），如果存在一個移動的點M（x，y）與兩個定點形成的角為90 度，那么M 點的軌跡方程是什么？

變式一：經過A（-5，0）的動態直線與經過B（3，0）動態直線之間形成90 度的直角，那么垂足M 的軌跡是什么？

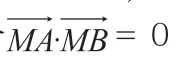
學生通過變式訓練就能夠發現，變式后和原題在本質上是相同的，僅僅在表達方面存在一定差異，學生只要將干擾因素排除，就會發現以AB 作直徑的圓即為M 點的運動軌跡，在兩種變式中，教師就可以引導學生使用不同的方法進行求解，從而讓學生更好地將理論知識用于實際，促進學生思維能力的提高。不難看出，變式訓練可以最大程度地發揮學生的潛力，使學生的解題能力得到進一步的提升。

總而言之，我們要提高學生的數學能力，不僅要掌握基礎知識，還應該在掌握基礎的概念、定理和公式等基礎知識之后，熟練應用變式教學，這樣才能在教學中對其靈活應用，促進學生解題水平的提高。