雙梁門式起重機靜動態特性分析

□彭 軍

一、引言

作為一種常見的起重運輸機械，門式起重機(以下簡稱門機)具有場地利用率高、作業范圍大、通用性強等優點，廣泛應用于鐵路及港口貨場等生產區域。門機工作時，主要承受由起重小車起吊貨物引起的垂向載荷，起升、運行及制動機構的啟停引發的沖擊載荷等，另外，由于貨物的擺動等原因，整機結構會承受來自各個方向的隨機振動，當外界振動載荷的頻率與結構的固有頻率接近時就會引發共振，造成結構更大的破壞。因此，在進行門機設計時非常有必要深入研究其靜動態特性。鄒湘等人[1]以某造船用門式起重機為研究對象，利用ANSYS Workbench對結構的剛度和模態進行了分析。劉磊[2]為了研究某單梁門式起重機的動態特性，利用有限元軟件對其開展了模態分析和瞬態動力學分析。馬世輝等人[3]則通過模態分析和諧響應分析來研究某桁架門式起重機的動態特性，獲取了結構的固有頻率、振型及易產生共振的頻率。文廣等人[4]和譚云波等人[5]均從靜動態特性分析的角度分別對桁架式門式起重機展開了研究，研究結果為門機結構的優化改進奠定了基礎。劉岳嵩等人[6]在研究某鋅合金門式起重機動態特性時發現，當起重小車位于主梁跨中和懸臂端時整機模態振型表現一致。韓偉等人[7]以某帶蒙皮的門機金屬結構為分析對象，利用ANSYS軟件對其模態特性和瞬態動力響應進行了分析，計算結果為起重機蒙皮的設計提供了理論依據。江愛華等人[8]從仿真和試驗的的角度對某門式起重機金屬結構的載荷響應進行了研究。本文以有限元軟件ANSYS作為計算工具，對某雙梁門式起重機金屬結構的靜、動態特性進行分析，獲取其靜強度、靜剛度、固有頻率及振型等指標參數，分析計算結果為接下來開展該門機金屬結構的優化設計奠定了理論基礎。

二、雙梁門式起重機金屬結構數值模型

該門機金屬結構如圖1所示。整機金屬結構均由Q235B材料制成，該材料的密度是7.85×10-6kg/mm3，材料的泊松比是0.3，材料的彈性模量是2.1×105MPa，材料的屈服強度是235MPa，按照起重機設計規范GB3811-2008[9]的相關規定，校核起重機金屬結構的強度時，應定義相應的安全系數，本文取1.34，通過計算得到該材料的許用應力為175MPa。

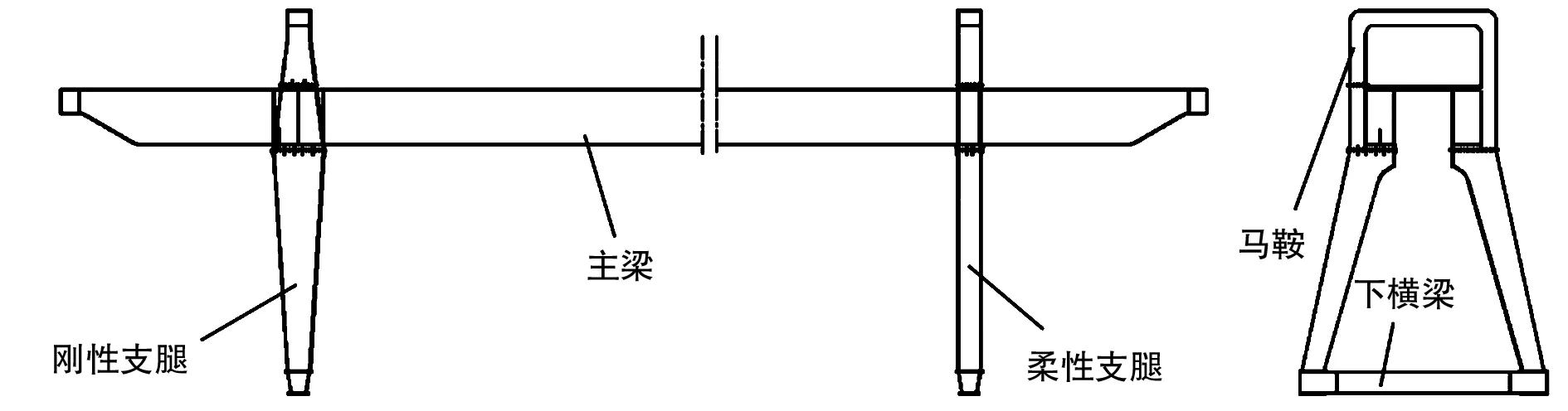
圖1 門機結構簡圖

分析時，建立該門機金屬結構的數值模型，選擇在有限元軟件ANSYS中實現。為了在保證計算精度的前提下盡量提高建模、分析計算的效率，按照結構有限元分析的建模原則忽略了起重機上的欄桿、電纜、軌道等附屬結構件。實體模型建立后，整機金屬結構使用shell181單元來模擬，網格劃分的方式則選用映射方式，網格劃分后，整機模型被離散為6,812個單元，節點的個數則為6,642。圖2給出了離散后的門機金屬結構數值模型。

圖2 門機金屬結構有限元模型

三、門式起重機金屬結構靜態特性計算結果

在建立該門機金屬結構數值模型基礎上，按照該門機金屬結構的實際工作條件定義其約束和載荷。考慮到大車運行軌道對起重機大車車輪的支撐作用，在該門機支腿與軌道接觸處，對整機金屬結構有限元模型施加相應的位移約束，具體的約束條件如下：在左端剛性支腿前部支承處，約束其沿小車軌道方向、豎直方向、大車軌道方向上的平動自由度，在左端剛性支腿后部支承處，約束其沿小車軌道方向、豎直方向上的平動自由度；在右端柔性支腿前部支承處，約束其沿大車軌道方向、豎直方向上的平動自由度，允許其沿小車軌道方向存在10mm的位移，在右端柔性支腿后部支承處，約束其沿豎直方向上的平動自由度，允許其沿小車軌道方向存在10mm的位移。主梁在工作時主要承受來自起重小車起吊貨物引起的垂向載荷，并且，起重小車會沿著主梁上方的軌道移動，為了全面分析該門機在工作載荷作用下的靜態特性，考慮起重小車分別位于主梁跨中、左右懸臂端等位置時的三種典型工況進行計算。該門機的額定起重量為20t，起重小車的質量為18.5t，計算時，考慮起重機的起升動載效應，將額定起重量和起重小車的重量相加并乘以起升動載系數后加載到主梁指定位置。通過計算得出該雙梁門式起重機金屬結構在指定工況下的等效應力及位移云圖(如圖3、圖4所示)。

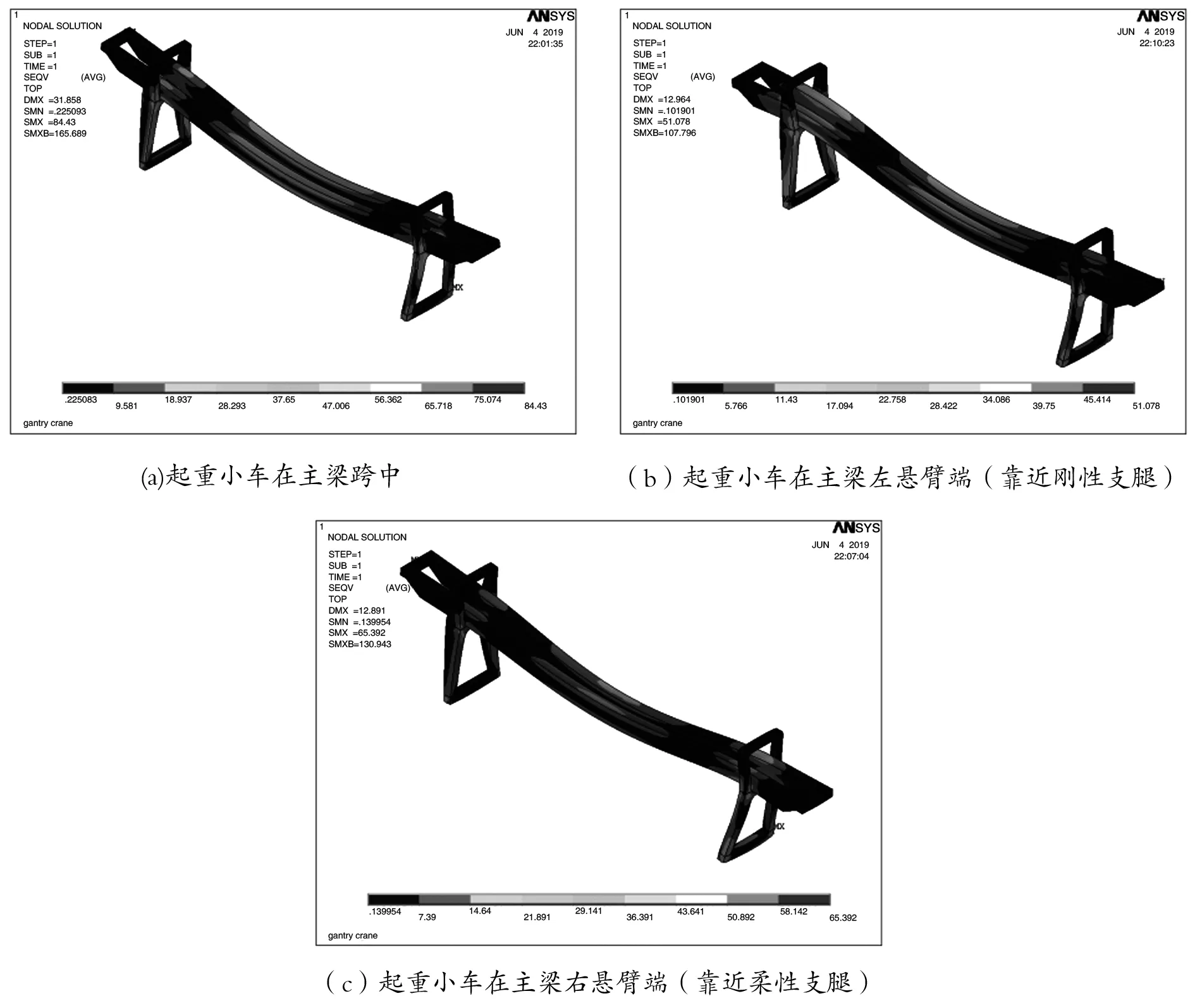
圖3 門機主梁工作應力云圖

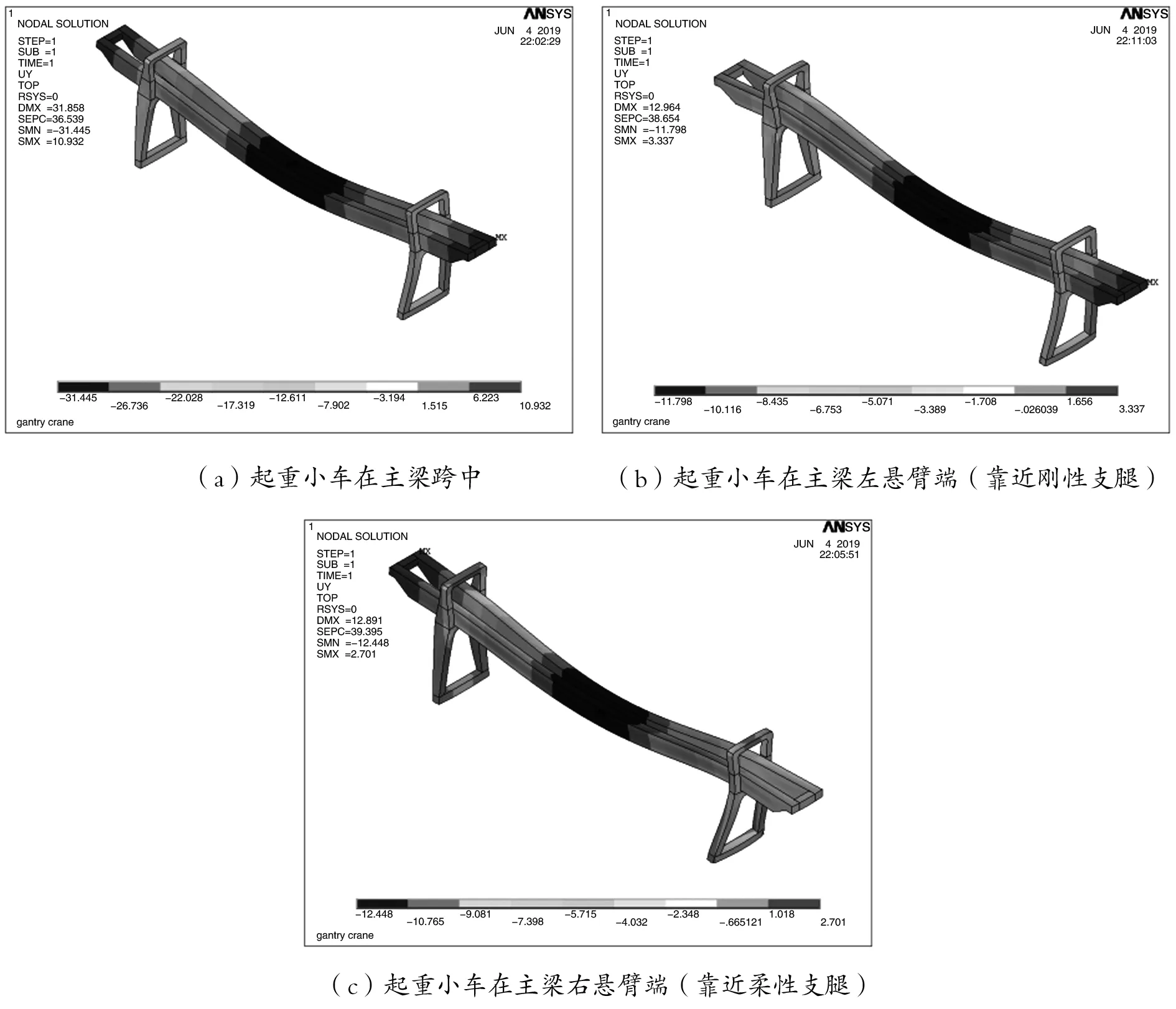
圖4 門機金屬結構豎直方向位移變形云圖

從圖3(a)可以看出，當起重小車位于主梁跨中時，最大應力發生在柔性支腿與下橫梁交接處，最大應力值約為84.43MPa，其值遠小于材料的許用應力值；從圖3(b)可以看出，當起重小車位于主梁左懸臂端時，結構最大工作應力發生在剛性支腿與下橫梁交接處，其值為51.078MPa，從圖3(c)可以看出，當起重小車位于主梁右懸臂端時，結構最大工作應力發生在柔性支腿與下橫梁交接處，其值為65.392MPa。

從圖4可以看出，在三種計算工況下，整機結構在豎直方向上的最大位移變形均發生在主梁跨中，其中，當起重小車位于主梁跨中時，其位移變形最大，變形值達到了31.445mm。

四、門式起重機金屬結構模態計算結果

模態分析和諧響應分析是基于有限元法的結構動力學分析中比較常見的類型，其中，對結構開展模態分析[10]主要是為了求解結構的振型和固有頻率等動態特性參數，對結構開展諧響應分析則是為了考察外界激勵載荷作用下結構的動態響應。

為了獲取該門機金屬結構的固有頻率和模態振型，利用蘭斯索斯法[11]，對該門機金屬結構進行模態分析。分析時需要定義模態提取及擴展階數，相對而言，結構動態特性對低階模態較為敏感，為了提高分析效率，本文只提取了該門機金屬結構的前6階模態。該雙梁門式起重機金屬結構的前6階固有頻率值如表1所示，圖5給出了該結構的前6階振型。

表1 門機金屬結構模態固有頻率 單位：Hz

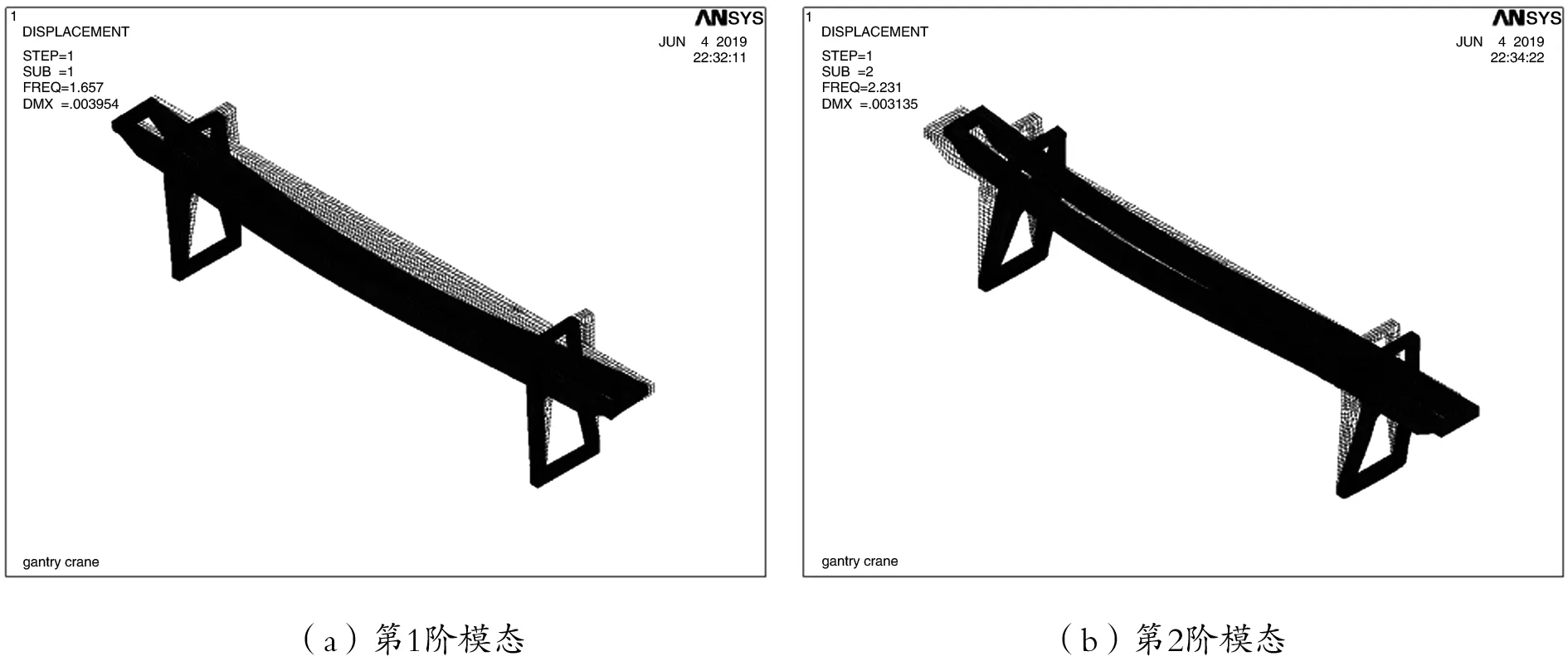
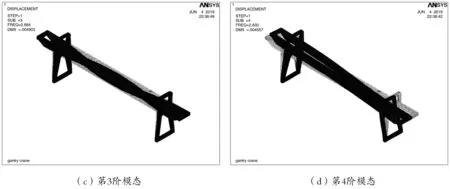
圖5 門機金屬結構模態振型圖

從圖5可以看出，該門機金屬結構的各階振型表現如下：第1、4、5階振型均為整機在前后方向(沿大車軌道)的擺動及主梁在水平面內的一階彎曲，第2階振型為整機在左右方向(沿小車軌道)的擺動及主梁的一階彎曲(在豎直平面內)，第3階振型為主梁的一階彎曲(在水平面內)，第6階振型為主梁在豎直面內的一階彎曲。

五、門式起重機金屬結構諧響應計算結果

為了考察外界激勵載荷作用下，該門機金屬結構的動態響應，找出結構動態特性更為敏感的模態，針對該門機金屬結構，開展了諧響應分析。分析時設置外界激勵頻率范圍，考慮到模態分析結果中提取的門機結構前六階固有頻率最大值為3.9252Hz，故將外界激勵載荷頻率變化范圍設置為0～4Hz，變化極差為0.1Hz，圖6給出了該雙梁門式起重機金屬結構主梁中部節點豎直方向的位移響應幅值—外界載荷激勵頻率曲線，從圖6可以看出，其位移響應幅值在激勵頻率為3.9Hz時達到最大，與上述整機金屬結構模態分析結果進行對比發現，該門機金屬結構的第6階模態固有頻率與激勵頻率3.9Hz接近，所以，可以認為該門機金屬結構的動態特性對第6階模態更為敏感，在對結構進行優化設計時應該重點分析該階模態的影響。

圖6 主梁中部節點位移響應幅值(豎直方向)

六、結語

本文利用有限元軟件ANSYS，對某雙梁門式起重機金屬結構的靜、動態特性進行了分析，計算了該門機金屬結構在工作載荷作用下的靜強度、靜剛度、模態固有頻率及振型等指標參數。通過分析得出如下結論。無論起重小車位于主梁跨中還是懸臂端，該門機金屬結構在工作載荷作用下承受的最大工作應力均沒有超過該材料的許用應力值，即，該雙梁門式起重機金屬結構的靜強度特性滿足設計要求。當起重小車位于主梁跨中時，主梁金屬結構產生的位移變形最大。該門機金屬結構在約束狀態下的前六階固有頻率分別為1.6567、2.2315、2.6844、2.8328、3.4355、3.9252Hz，其中，第1、4、5階振型均為整機金屬結構的擺動(沿大車軌道方向)及主梁的一階彎曲(在水平面內)，第2階振型則為整機的擺動(沿小車軌道)及主梁的一階彎曲(在豎直面內)，第3階振型為主梁的一階彎曲(在水平面內)，第6階振型為主梁的一階彎曲(在豎直面內)。該門機金屬結構的振動響應幅值曲線在外界激勵載荷頻率為3.9Hz時，達到了最大峰值，結構的第6階模態固有頻率與該激勵頻率最接近，該結構的動態特性階對第6階模態更為敏感。