基于EnKF和RSSI的井下人員跟蹤定位研究

郭落樂

(晉城煤業集團 寺河礦， 山西 晉城 048205)

煤礦井下作業遠離地面，生產系統及地質條件復雜，面臨著煤與瓦斯突出、礦井火災、透水、冒頂等突發事故的威脅，因此，為了保證工作人員的安全，建立一套可靠的井下人員精確定位系統具有重要的意義[1-3].可靠的人員定位對煤礦安全生產和災后救援工作都能起到積極作用。

當前，發展較為成熟的定位系統(GPS全球定位系統和蜂窩無線定位系統)由于井下巷道系統復雜對電磁波易造成干擾和衰落，增加了井下人員跟蹤的難度[4]，并不適用于井下人員定位。隨著無線傳感器網絡( Wire-less Sensor Network，WSN ) 高速發展并且日漸成熟，無線傳感器節點逐漸在井下環境設備及人員的定位與跟蹤中應用，而常用的定位算法主要是RSSI(接收信號強度)定位算法[5]. RSSI是基于測距的定位算法，其定位結果不具備連續性、遞推性和自適應性，無法實時跟蹤人員位置并且無法對人員的運動狀態進行良好的估計[6]. 井下人員或車輛的運動常為非線性的運動目標，非線性運動的性質增加了井下人員跟蹤定位的難度。卡爾曼濾波一般用于線性系統的預測矯正，但當人員做強非線性運動時，卡爾曼濾波的預測矯正性能將得不到發揮。1994年由Geir Evensen提出的集合卡爾曼濾波算法(EnKF)是引入集合預報思想的一種非線性濾波方法，它將集合預報思想和卡爾曼濾波算法結合起來，解決了非線性系統中使用卡爾曼濾波算法的近似問題，適合應用于非線性系統的預測矯正[7,8]. 集合卡爾曼濾波作為一個連續的數據同化(DA)的方法，采用合并模型預測和當前觀測值的方式產生一個潛在的系統狀態最優估計。由于EnKF具有高效性、可擴展性和易于并行計算的優點，在近幾十年內已被廣泛應用于地球科學和大氣污染以及其他動態狀態估計中[9-12]. 本文提出了將集合卡爾曼濾波與RSSI相結合用于井下人員跟蹤定位的方法，利用集合卡爾曼濾波減小噪聲對定位模型的影響，提高定位的精度。

1 定位方法

1.1 RSSI定位算法

依據RSSI值與距離的特定關系，建立簡化的井下人員定位的數學模型為[13]：

RSSI=—(10nlgd+S)

(1)

式中，n為路徑損耗系數；d為參考節點與定位節點間的距離；S為當參考節點與定位節點間距離d為1 m時所測得的RSSI值。

在測得參考節點與定位節點間相對精確的距離di后，使用空間距離后方交會法，可以確定定位節點一定在以參考節點為圓心，di為半徑的球面上，在得到井下人員即定位節點與3個參考節點之間的距離后，可以得到3個球面，那么3個球面相交的點就是定位節點。

計算得到參考點與定位節點之間的距離為dn，使用其對應的坐標值與距離值可以列出下列方程組：

(2)

在實際應用中可能會由于測量誤差的存在，導致方程組(2)的無解，運用全交點質心法作為定位算法，可以將方程組(2)轉換成方程組(3)：

(3)

式(3)可簡化為：

Kα=s

(4)

其中：

利用最小二乘法求解式(4)，即可得所求定位節點的定位坐標。

1.2 集合卡爾曼濾波模型

集合卡爾曼濾波的系統狀態和系統觀測可表示為：

x(tk)=M[x(tk-1)]+η

(5)

y(tk)=H[x(tk)]+ε

(6)

式中，x是動力系統的狀態向量，tk和tk-1表示時間步，M(x)是人員的運動模型,η是人員運動模型的誤差,y是系統的觀測向量,H(x)是觀測模型，ε是觀測誤差。

為了滿足人員運動狀態的非線性和隨機性，采用人員運動模型：

(7)

vt=vt-1+at-1t

(8)

at=ωt

(9)

其中，加速度at為隨機數，符合一定條件的隨機分布，這樣不僅實現了運動模型的強非線性，并且更加符合實際的井下人員運動情況；vt為t時刻的人員速度；st為t時刻的人員位置坐標。

觀測模型H(x)用于狀態向量的矩陣變換，即將狀態向量中的參數映射到觀測區域。在該實例中，狀態向量中僅有人員位置坐標一個參數，同時可觀測信息也同樣為人員位置坐標，因而H(x)可計算如下：

H(x)=x

(10)

集合卡爾曼濾波模型分為預測和更新兩個步驟，分別按下式計算：

(11)

(12)

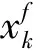
(13)

(14)

Ke=PeHT(HPeHT+Re)-1

(15)

式中，Re是觀測誤差協方差矩陣，即為觀測噪聲；Pe是狀態預測誤差協方差矩陣；N表示集合的數量大小，該實例中取為60. EnKF的誤差協方差矩陣通過有限個集合成員得出，用集合的思想解決了卡爾曼濾波算法在非線性運動目標跟蹤定位中估計和預測誤差協方差矩陣比較困難的問題。

2 定位仿真分析

為了驗證該人員定位方法的精確性和實用性，對一個線性運動狀態和兩個非線性運動狀態進行仿真分析。其中兩個非線性運動的定位目標中，一個定位目標做加速度a符合(-0.4～0.6)隨機分布的變加速運動，另一個定位目標的運動情況符合：勻速運動—加速運動—減速運動—勻速運動，由此，這兩個定位目標的運動狀態具有了強非線性的特點。為了模擬由于礦井復雜環境及人員運動所造成的電磁波干擾和衰落而導致的定位誤差，對線性運動定位目標添加了符合(0～5 m)隨機分布的噪聲,對非線性運動目標添加了符合(0～10 m)隨機分布的噪聲。3個定位目標的運動參數設置見表1.

表1 3個定位目標的運動參數設置表

由于在EnKF定位方法的實際操作中，定位目標的真實初始速度不可預測，因此集合卡爾曼濾波模型只能輸入一個先驗的初始速度，在先驗初始速度與真實初始速度之間的誤差將通過集合卡爾曼濾波算法利用觀測值來進行矯正。在該仿真分析中，設置集合卡爾曼濾波模型的集合數量[7]為60，先驗初始速度與真實初始速度的設置見圖1.

3個定位目標的定位及定位絕對誤差情況見圖2，3，4.

圖2表明當定位目標為線性運動狀態時，EnKF定位模型可以借助RSSI定位算法所得到的位置信息

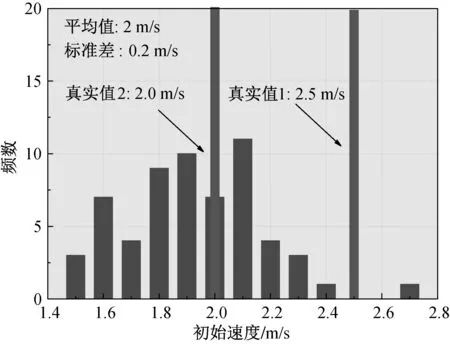
圖1 先驗初始速度設置圖

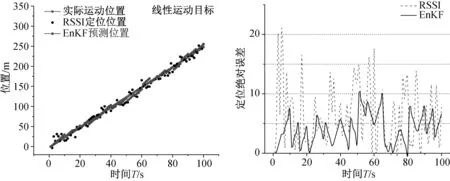
圖2 線性運動目標定位情況及誤差圖

作為觀測值，實現對運動目標的連續定位，并且定位精度也得到明顯提高。即使給定位目標添加了0～5 m隨機分布的噪聲，EnKF模型定位的絕對誤差絕對值在10 m之內的比例達到了99%，在5 m之內的比例為67%，而RSSI定位絕對誤差絕對值在10 m之內的比例只有79%，在5 m之內的比例為46%，與RSSI定位的結果相比較，EnKF模型定位的結果有更良好的參考價值。

從圖3和圖4中可以看出，EnKF定位模型對兩種非線性運動目標的定位效果，由于非線性運動目標定位添加了較大的噪聲，并且非線性運動加大了EnKF模型跟蹤定位的難度，因此其結果與線性目標定位相比有較大的定位誤差。但是由于EnKF定位方法結合了RSSI定位與運動模型，有效減輕了RSSI定位的隨機誤差，在兩種非線性運動目標定位中均取得了比RSSI定位更加精確的結果。其中，非線性運動目標1的EnKF定位絕對誤差絕對值小于10 m的比例為64%，小于15 m的比例為90%；非線性運動目

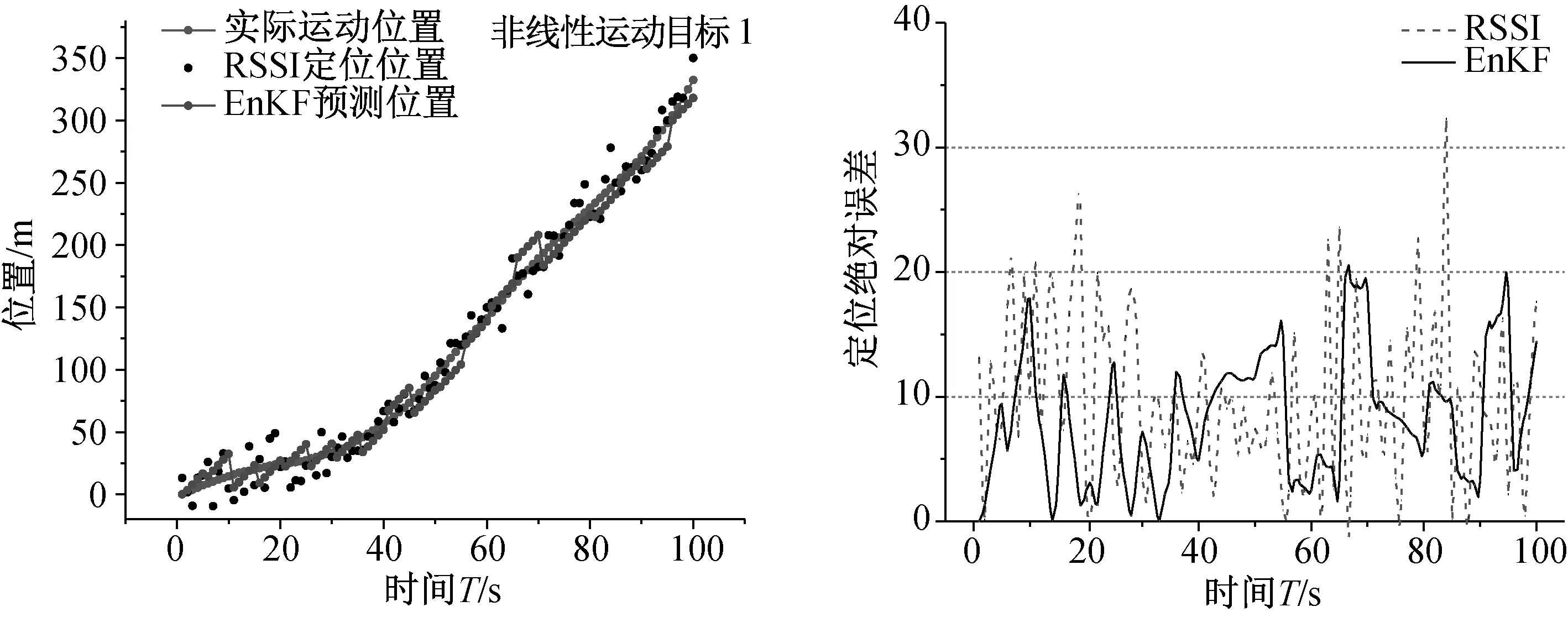
圖3 非線性運動目標1的定位情況及誤差圖

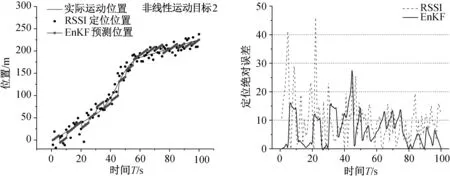
圖4 線性運動目標2的定位情況及誤差圖

標2的EnKF定位絕對誤差絕對值小于10 m的比例為70%，小于15 m的比例為96%. 而RSSI對兩個非線性運動目標的定位誤差絕對值小于10 m的比例分別為58%和54%，小于15 m的比例分別為77%和82%. 因此，EnKF定位模型在井下非線性運動目標定位中同樣可以取得比RSSI定位更加精確可靠的結果。

3 敏感性分析

在EnKF定位方法中，先驗的初始速度中有很大的不確定性，這很可能對定位的結果造成影響。因此，為了驗證該方法的實用性，在非線性運動目標2的定位仿真中對先驗的初始速度進行了敏感性分析。使用不同先驗初始速度的定位情況及誤差見圖5.

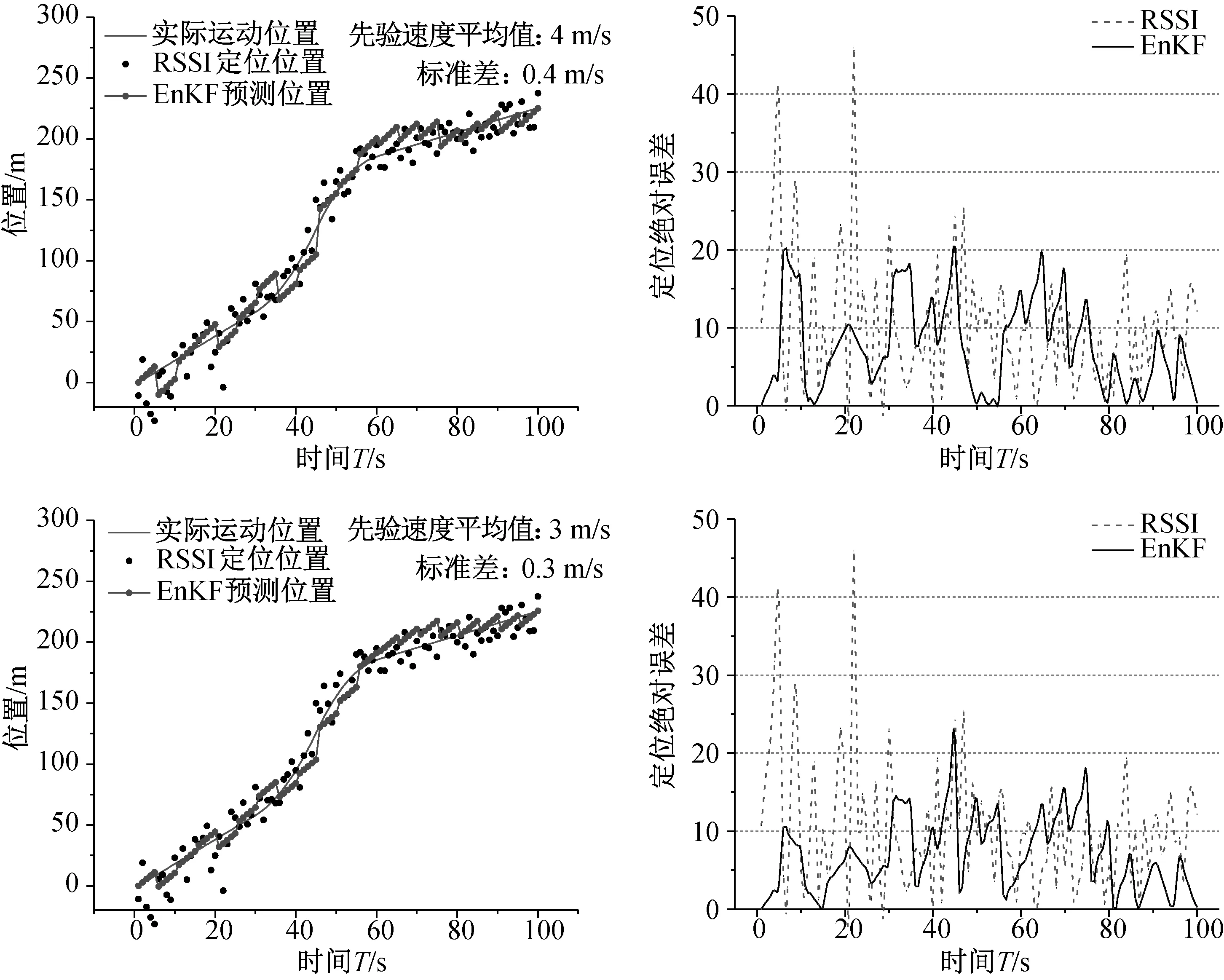
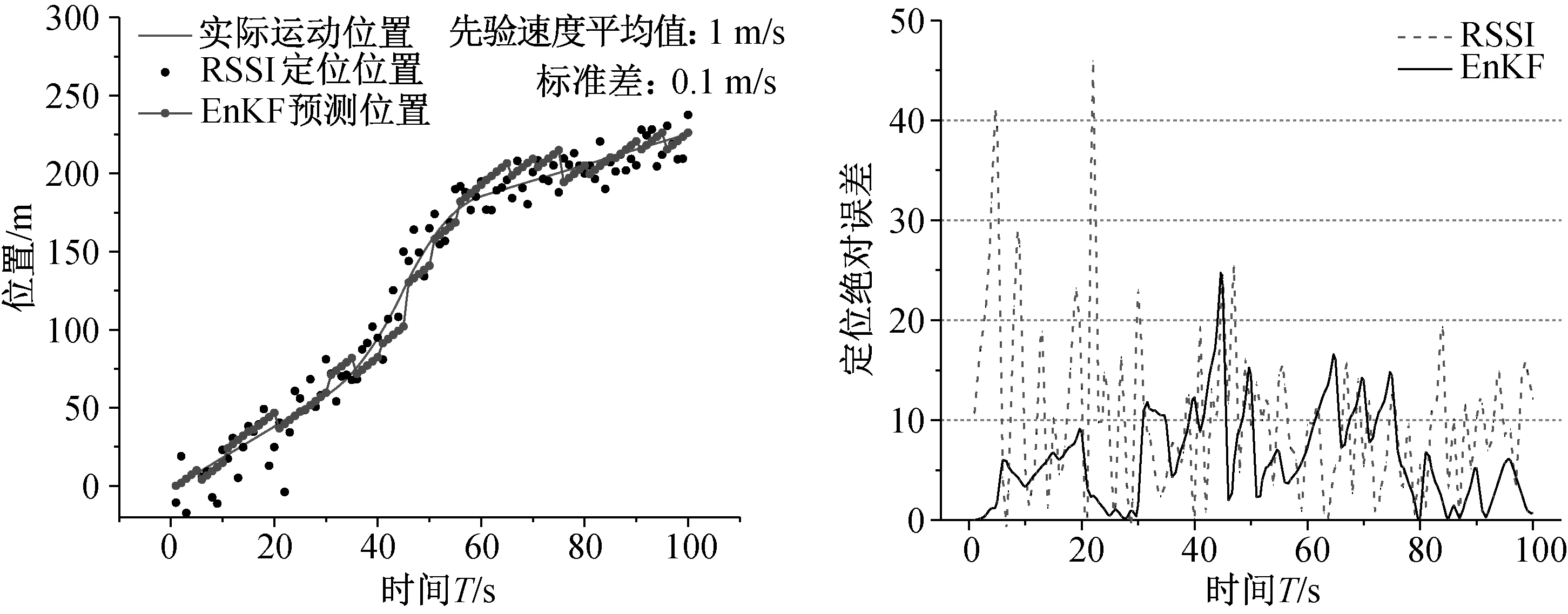
圖5 使用不同先驗初始速度的定位情況及誤差圖

從圖5中可以看出，當先驗初始速度取不同值時，EnKF方法定位的結果均比RSSI定位的結果有所提高。在非線性目標2的定位中，先驗初始速度的平均值分別為：4 m/s，3 m/s，2 m/s和1 m/s時，其定位絕對誤差絕對值小于10 m的比例分別為：66%、73%、70%和79%，小于15 m的比例分別為：85%、95%、96%和96%. 這說明即使先驗初始速度與真實初始速度之間的誤差大小不一，通過EnKF算法的預測矯正，在先驗初始速度中存在的誤差都會被有效抑制，達到精確性類似的跟蹤定位結果。因此，該EnKF跟蹤定位方法對先驗初始速度的敏感性較差，當先驗初始速度中含有較多的誤差時，依然可以得到較好的定位結果。所以，該方法在井下運動目標的跟蹤定位上具有很強的實用價值。

4 結 論

提出了集合卡爾曼濾波(EnKF)與無線信號接收強度(RSSI)定位算法相結合的井下人員跟蹤定位方法，該方法通過集合卡爾曼濾波算法減小多種噪聲對定位的影響，可得到連續的人員跟蹤定位結果。經過仿真實驗表明，該方法在線性與非線性運動目標的定位中性能均優于RSSI定位，即使跟蹤定位受到較大的誤差影響，依然可以取得良好的定位效果。通過先驗初始速度的敏感性分析得出，當先驗初始速度中含有較多的誤差時，該方法依然可以得到較好的定位效果，具有較強的實用性。