基于精英蜂群算法的配電網故障恢復方法

李倫 李棕讓 曹興華 楊鑫 崔璨 朱宗峰 陳雪峰 宮德鋒

摘要：? 為縮短故障停電時間，降低停電損失，尋找最佳供電恢復方案，本文建立了配電網故障恢復數學模型，并引入精英蜂群算法，構建精英蜂群策略，改進偵查蜂搜索機制，得到配電網故障恢復的整體流程。同時，以某地市供電公司實際配電網系統故障恢復供電案例為例，分別采用標準人工蜂群算法（artificial bee colony， ABC）和精英蜂群算法對目標函數進行運算，并比較兩種方法的可行性與優越性。研究結果表明，精英蜂群算法的收斂性能明顯好于標準的ABC算法，其對配電網故障后重構的優化結果更好，是一種非常有效且非常實用的配電網故障恢復方法。該研究為配電網故障恢復方法研究提供重要參考，對社會經濟的發展具有重要意義。

關鍵詞：? 配電網;故障恢復;精英蜂群;數學模型;案例分析;停電時間

中圖分類號： TM642+.2; TM711? 文獻標識碼： A

配電網是電力輸送的“最后十公里”，是國民經濟和社會發展的重要公共基礎設施，配電網的規模直接制約城市與農村的發展[1] 。近年來，配電網投資力度不斷加大，但由于歷史的原因，配電網尤其是中壓配電網發展仍然滯后，城市與農村、東部與中西部電網發展不平衡問題依然突出[2] ，供電可靠性與國際先進水平仍有較大差距，存在著整體發展滯后與地區發展不平衡（城農不平衡、東中西部不平衡）的問題[3] 。由于自身因素的影響，配電網出現接地、跳閘等故障的頻率較高，配電網故障直接導致電力用戶失去電力供應，造成經濟損失，影響供電公司品牌形象[4] 。為優化營商環境，保證用戶電力供應，提供優化電能，配電網故障恢復方法研究成為電力系統研究的熱點。馬天祥等人[5] 針對交直流混合配電網特殊的網架結構和電氣特性及交直流混合配電網故障恢復模型，研究了基于二進制粒子群算法的交直流混合配電網故障恢復方法，提出適用于交直流混合配電網故障恢復問的模型，模型應用適用較小，在傳統交流配電網中應用較少;陳瑋[6] 考慮主動配電網中風光機組出力不確定因素，將電動汽車作為應急調度資源，建立了一個形式為min-max-min的三層魯棒數學模型，但模型中對配電網故障后恢復涉及較少;宋毅[7] 依托一體化電網規劃設計平臺，研究基于智能軟開關的有源配電網供電恢復方法，在配電網發生故障并隔離后，智能軟開關可為失電區域提供有效的電壓支撐，該恢復方法結構較為復雜，推廣應用存在一定難度。基于此，本文在配電網故障恢復方法中引入精英蜂群算法，利用其尋優率、求解精度高、收斂速度快等優點，以降低停電網損為目標，建立基于配電網故障恢復方法，并以某地市實際配電網部分網絡結構為例，實際驗證該算法的可行性與準確性，能夠減少網損，對降低電力損失，為電力企業具有良好的經濟效益。

1 配電網故障恢復數學模型

配電網可看成是由許多分段開關、聯絡開關及架空線路、電纜線路和用戶組成，開關的閉合和斷開都會造成網絡拓撲結構的變化，配電網的重構通過調整開關狀態來達到改變配電網拓撲結構的目的[8] 。實際運行中的系統都反映不同的運行條件，因此配電網需要根據具體的運行條件進行重構。

配電網故障恢復是一個復雜的工程問題，歸根結底屬于求解最優化問題[9] 。在進行故障恢復時，首先采用等效負荷模型簡化網絡，即把該問題轉化為數學領域的問題。故障恢復由恢復目標和約束條件兩部分組成，實際情況下可以按照不同的恢復目的和側重點進行建模[10 11] 。配電網故障恢復模型為

minf S，X h S，X =0 g S，X ≤0 S∈T? （1）

式中，f（S，X）是所建立數學模型的目標函數，S是控制變量，X是狀態變量;h是等式約束條件;g是不等式約束條件;T是所求問題的可行解空間。

1.1 建立數學模型

對所要求的故障恢復目標，建立如下數學模型：

1） 要求恢復的負荷量最多，即失電負荷最小，其目標函數為

minLout =∑ n0 i=1 Pi-PS （2）

式中，n0為停電區節點總數;Pi為停電負荷節點i的負荷量;PS為恢復方案的最大恢復容量;Lout 為失電負荷量。

2） 要求網損最小，其目標函數為

minSloss =∑ n k=1 I2kRk （3）

式中，Ik為線路k上的電流;Rk為線路k的電阻;n為支路總數。

3） 要求開關操作總數最少，其目標函數為

minNum=∑ n i=1 |xi-x′ i|?（4）

式中，n為線路開關總數;xi為開關i故障前狀態;x′i為恢復后的開關狀態。

4） 以負荷均衡為目標，其目標函數為

minF=∑ n b=1 P2b+Q2b S2bmax? （5）

式中，n為網絡中閉合的支路總數;Pb，Qb，Sbmax 分別為支路b的有功功率、無功功率及允許的最大容量。

1.2 約束條件

在恢復過程中，配電網故障要時刻滿足如下約束條件：

1） 輻射狀運行的網絡約束為

gk∈Gk （6）

式中，gk為當前的網絡結構;Gk是所有允許的輻射狀網絡配置集合。

2） 線路容量約束為

Il≤Ipl ， l=1，…，Li （7）

式中，Il是經過設備的電流;Ipl 為允許流過的電流上限;Li是設備總數。

3） 節點電壓約束為

Uimin ≤Ui≤Uimax ， i=1，…，m （8）

式中，m為開關總數;Ui，Uimax ，Uimin 分別為開關i上的電壓、電壓最大值和最小值。

由以上分析可知，配電網故障恢復問題是一個包含約束條件的多目標非線性離散問題。本章采用改進蜂群算法的故障恢復模型，并可根據故障恢復目標的要求，建立目標函數。考慮網損和失電負荷，可建立目標函數為

minf=αLout +βSloss? （9）

式中，α和β分別為失電負荷量和網損權重;Lout 及Sloss 的求解見式（2）和式（3），該目標函數同樣需要滿足式（6）～式（8）所列的約束條件。

2 精英蜂群優化算法

蜂群算法的基本思想，首先將蜂群劃分為引領蜂、跟隨蜂和偵察蜂三種蜂種，然后隨機生成初始種群，算法會在適應度值較優的一半個體周圍進行搜索，采用一對一的競爭策略選擇較優個體，該過程為引領蜂的搜索過程;利用輪盤賭選擇法選取較優個體，并對其領域進行貪婪搜索，產生另一半個體，此過程稱為跟隨蜂的搜索過程[12 13] ;將引領峰和跟隨蜂產生的個體組成新的種群，為避免種群多樣性喪失，進行偵察蜂的類變異搜索，形成迭代群。與其他雜交優化算法相比，精英蜂群算法通過構建精英蜂群策略、改進偵察蜂搜索機制以及基于目標函數值選擇尋優等方式，實現了精英蜂群算法能夠加速算法收斂，同時不易陷入局部最優的效果[14] 。

2.1 精英蜂群策略的構建

采用按比例的適應度進行蜂群算法的選擇，體現了生物學中“適者生存、優勝劣汰”的進化過程。智能算法在搜索最優解的過程中容易陷入局部最優，適當變異這些適應度值差的個體，可能會使算法跳出局部最優，最終收斂到全局最優[15 16] 。因此，精英蜂群通過選取排名前ζ%的精英蜂群，利用精英蜂群的記憶信息庫，在蜂群位置發生變化時，一只精英蜂參與雇傭蜂和跟隨蜂的局部位置更新，指導雇傭蜂和跟隨蜂，此時精英蜂群受偵察蜂的全局引導，實現了優質食物源位置更新，達到了不易陷入局部最優的效果[17] 。新的雇傭蜂和跟隨蜂位置更新策略為

υi，j =χe，j +φi，j w（χk，j -xave，j ） （10）

其中

φi，j =rand（-1，1）;ω= ωmax - iter MCN ωmax -ωmin? ; χave，j = ∑ D j=1 χi /D

式中，χe，j 表示精英蜂群隨機一只精英蜂的第j維空間位置分量;ω表示精英蜂的權重系數;χave，j 表示蜜源第j維位置分量的平均之值;D表示空間維數。

2.2 改進偵查蜂搜索機制

傳統人工蟻群算法設置是當食物接近枯竭時，雇傭蜂會轉為偵查蜂來尋找新的食物源。將混沌序列算子和偵察蜂的歷史經驗值相結合來代替隨機分布解空間，完成防止陷入局部最優的尋食過程[18] 。由于混沌序列具有較好的隨機性和遍歷性，本文基于混沌序列，在偵查蜂全局搜索時，結合歷史搜索位置信息，對局部尋優進行指導，及時與跟隨蜂完成信息交換，放棄跟隨蜂尋覓到的枯竭食物源，開始新的蜜源搜索，重復以上過程，實現全局最優解。

1） 偵查蜂的初始分配方法。將各個解的可行域劃分為ms等份，并將ms只偵查蜂分配于ms個子空間。設偵查蜂的初始位置[19] 為

χi，j （t0）=lbj+i（ubj-lbj）/m （11）

式中，i為偵查蜂的序號，i=1，2…ms，j=1，2…D。

2） 偵查蜂的偵查策略。由于偵查蜂需要在一定區域內四處游走尋找食物，因此其具有較強的隨機性和遍歷性。此外，該過程會受到以前經驗位置的影響[20] ，因此本文算法引入混沌序列，體現偵查蜂的隨機性和遍歷性的特性。同時，由于該過程會受到歷史偵查信息的影響，借鑒于粒子群算法，本文設置一個混沌搜索項來體現偵查蜂的隨機性和大視域的遍歷性，再設置一個啟發項，來體現偵查蜂在尋找食物過程中所受到歷史經驗的影響。整個偵查蜂尋食過程為

xi，j （t+1）=xi，j （t）+r1（t+1） lbj+i （ubj-lbj） m + r2（t）（xg，j -xi，j （t））， i=1，2…，m， j=1，2…，D （12）

rk（t）=μ（rk（t-1）（1-rk（t-1）））， rk（t）∈（0，1）， k=1，2， rk（t0）=rand（0，1）， ms=γm （13）

式中，xi，j （t）為在解空間的當前位置;xi，j （t+1）為搜尋后的位置;rk（t）為兩個不同混沌序列;rk（t0）為混沌序列的初值。

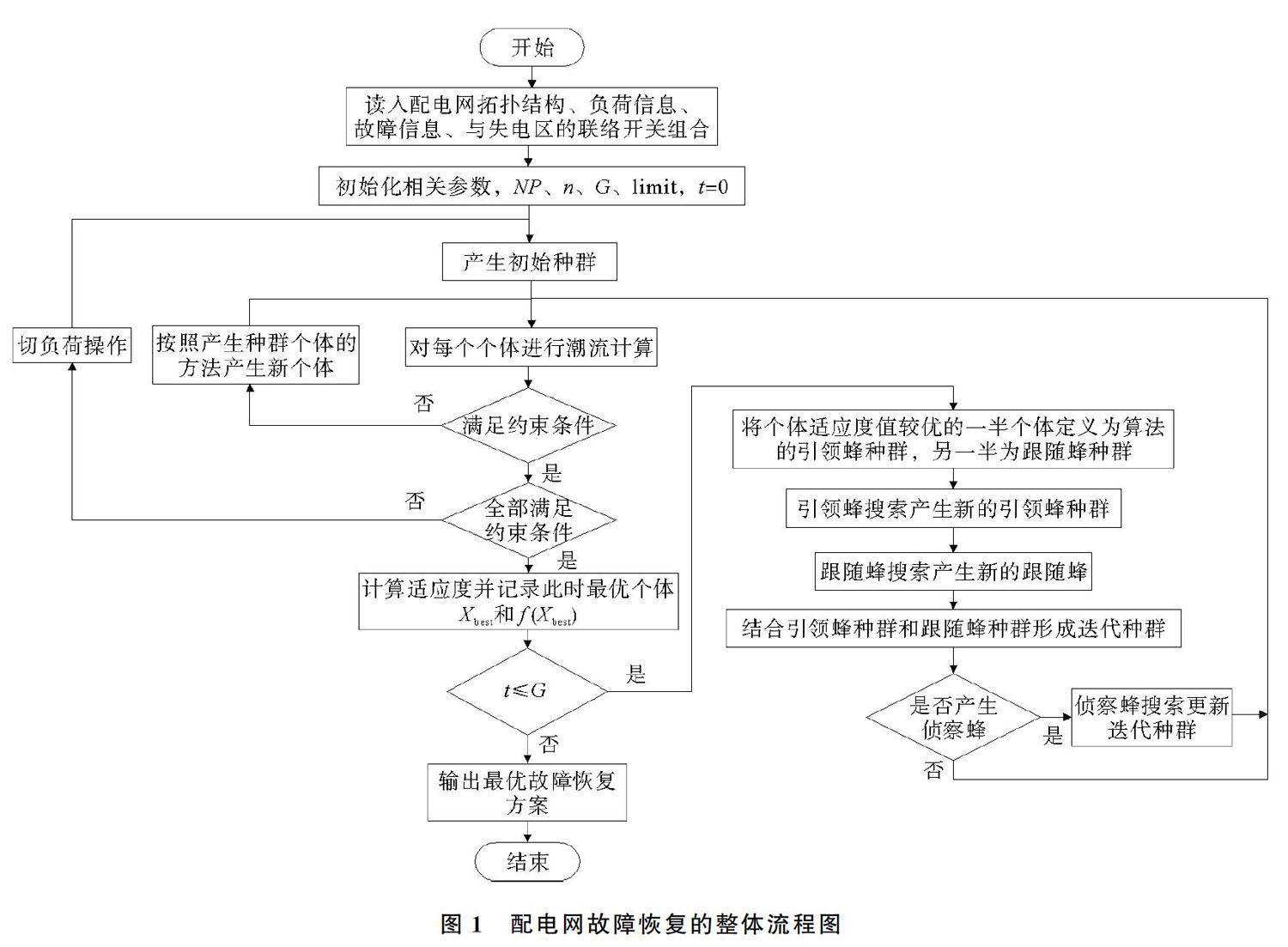
2.3 基于精英蜂群算法的配電網故障恢復整體流程

1） 根據配電網的拓撲結構來初始化參數，包括網絡拓撲信息、負荷信息、故障信息、與失電區相連的聯絡開關、種群規模NP、雇傭蜂數me，偵查蜂數ms，引領蜂數mo，個體維數n和最大進化代數G，進化代數初始值t=0。

2） 根據式（11），對me只雇傭蜂進行初始化設置，并實現偵查蜂的分配，產生初始個體，根據潮流計算結果，檢驗結果是否滿足約束條件，若滿足，則進行下一步驟;否則放棄該個體，重復步驟2），直到滿足種群規模NP，如果都不滿足，則需要從末端進行切負荷。

3） 根據潮流計算結果，計算種群中個體的適應度函數值，選擇其中的最優個體xtbest 和最優適應度值f（xtbest ） 。

4） 偵查蜂作大視域全局搜索，初始化混沌搜索項和啟發項，根據式（11），求解每只偵查蜂的解空間位置，并完成邊界檢查和轉換，求解ms只偵查蜂的適應度函數值。

5） 將適應度值較優的一半個體構成引領蜂種群，其余個體為跟隨蜂種群。

6） 將引領蜂種群中的個體按式（12）和式（13）搜索，產生新個體，計算其適應度值，擇優保留形成新的引領蜂種群。

7） 根據按適應度排序的蜜源，選擇計算與xi相關的概率Pi。

8） 跟隨蜂根據Pi，按式（12）和式（13）產生新解，形成跟隨蜂種群，并計算其目標函數值。

9） 判斷是否有連續nlimit 代沒有發生變化的解，若有，則變為偵察蜂，用下式形成新解來替換較差的解，即

V（j）=xti（j）+（-1+2rand）（xti（j）-xtr1 （j））

10） 通過潮流計算，確定并記錄本代種群最優個體和最優解。

11） 若滿足終止條件，輸出最優恢復方案，否則轉至步驟4）。

配電網故障恢復的整體流程圖如圖1所示。

3 配電網故障恢復案例分析

本文以某地市供電公司實際配電網系統為例，該配電網絡有46條支路，50個節點。其中，46條支路為不同型號的電纜接線，在區域內110 kV變電站中，有2臺正常運行的110 kV/10 kV配電變壓器，有2條110 kV進線，且與110 kV母線互為備用，2臺10 kV變壓器，出線通過聯絡開關B1連接。在網架結構內，共選取9個聯絡開關，標記為B1～B9。為計算方便，10 kV母線編號為3～50。同時，為了表示配電網中多電源的特點，將所選試點區域其他10 kV進線標記為10-1 ～10-9 。某地市供電公司實際配電網系統如圖2所示。

當10 kV電纜線路遇到外力損壞、絕緣受潮、化學腐蝕等情況時，絕緣將會降低，從而被擊穿，由此引發故障。例如，在所選配的電網區域內，母線3與14之間支路和母線43與45之間支路發生運行故障時，在遙控或人工切除該線路后，可以通過聯絡開關以及某些分段開關開合操作，調整配電網的運行方式，從而恢復非故障區域的供電。

由于該配電系統可以通過關閉聯絡開關，實現失電負荷為零和開關操作數少的目標，為了驗證算法的收斂效果，本文以網損最小為目標，對配電網進行恢復供電，即故障后重構。網損最小的收斂效果如圖3所示。利用式（3）所給出的目標函數，算法中種群規模為20，nlimit =D×ne×2，ne=NP/2為引領蜂個體數;溫度T=1000，降溫因子為η=0.95，終止溫度為10;最大迭代次數為60次。分別采用標準ABC和精英蜂群算法，對目標函數進行運算，并比較兩者的性能。由圖3可以看出，精英蜂群算法的收斂性能明顯優于標準ABC算法。

4 結束語

本文主要對基于蜂群算法的配電網故障恢復方法進行研究。針對網損最小，將改進后的蜂群算法與標準算法、遺傳算法和粒子群算法進行仿真性能對比，仿真結果表明，在配電網故障后重構應用中，精英蜂群算法具有優越的收斂性能，電網重構效果得以優化。該算法在實際應用中具有良好的可行性與準確性，能夠減少配電網故障后網損，節約電力資源，縮減電力成本，是一種非常有效并且非常實用的配電網故障恢復方法。該研究可為經濟社會的發展帶來巨大的經濟效益。

參考文獻：

[1] 張旭， 魏娟， 趙冬梅， 等. 電網故障診斷的研究歷程及展望[J]. 電網技術， 2013， 37（10）： 2745 2753.

[2] 肖隆恩， 李閆遠， 熊洋建， 等. 電網故障診斷的研究現狀與發展趨勢[J]. 通信電源技術， 2015（5）： 221 223， 226.

[3] 李春輝. 提高配網故障快速復電效率的思考與建議[J]. 科技與創新， 2014（18）： 23 24.

[4] 寇為剛， 李永祥， 孫艷軍. 電力系統故障診斷的研究現狀與展望綜述[J]. 自動化與儀器儀表， 2015（2）： 4 6， 9.

[5] 馬天祥， 王春英， 賈靜然， 等. 基于二進制粒子群算法的交直流混合配電網故障恢復方法[J]. 電力系統保護與控制， 2019， 47（9）： 112 119.

[6] 陳瑋. 模塊化多電平柔性直流輸電系統控制策略的研究[D]. 呼和浩特： 內蒙古工業大學， 2017.

[7] 宋毅， 薛振宇， 滕林， 等. 面向一體化配電網規劃設計平臺的數據集成技術研究及應用[J]. 電網技術， 2016， 40（7）： 2199 2205.

[8] 孫元博， 張承學， 胡志堅. 地區配電網重構與故障恢復問題[J]. 電網技術， 2014， 38（12）： 3366 3371.

[9] 洪小雨. 主動配電網故障恢復重構研究[D]. 北京： 北京交通大學， 2014.

[10] 許寅， 和敬涵， 王穎， 等. 韌性背景下的配網故障恢復研究綜述及展望[J]. 電工技術學報， 2019， 34（16）： 3416 3429.

[11] 馬瑞， 張海波， 王建雄， 等. 考慮負荷時變性的配電網故障搶修恢復策略[J]. 電力科學與技術學報， 2019， 34（2）： 20 27.

[12] 王林川， 李慶鑫， 劉新全， 等. 基于改進蟻群算法的配電網故障定位[J]. 電力系統保護與控制， 2008， 36（22）： 29 33， 53.

[13] 周坤. 改進的蟻群算法在城市配電網故障恢復中的應用研究[D]. 天津： 天津理工大學， 2015.

[14] 馬衛， 孫正興. 基于精英蜂群搜索策略的人工蜂群算法[J]. 計算機應用， 2014， 34（8）： 2299 2305.

[15] 李世光， 吳嬈， 高正中， 等. 基于改進人工蜂群算法的配電網故障恢復[J]. 中國科技論文， 2016， 11（11）： 1269 1274.

[16] 左思然， 王中宇， 范聞博， 等. 一種改進的人工蜂群配電網狀態估計方法[J]. 電測與儀表， 2018， 55（24）： 40 45.

[17] 高兆麗， 胥明凱， 丁素英， 等. 基于改進人工蜂群算法的配電網多點故障應急搶修優化調度[J]. 電力系統保護與控制， 2019， 47（13）： 107 114.

[18] ZHU Q B， YANG Z J， MA W. A quickly convergent continuousant colony optimization algorithm with scout ants[J]. Applied Mathematics and Computation， 2011， 218（5）： 1805 1819.

[19] Baraniuk R G. Compressive sensing [Lecture Notes][J]. IEEE Signal Processing Magazine， 2007， 24（4）： 118 121.

[20] Candes E J， Wakin M B， Wakin M B. An introduction to compressive sampling[J]. IEEE Signal Processing Magazine， 2008， 25（2）： 21 30.

Distribution Network Fault Recovery Method Based on Elite Bee Colony Algorithm

LI Lun， LI Zongrang， CAO Xinghua， YANG Xin， CUI Can， ZHU Zongfeng， CHEN Xuefeng， GONG Defeng

（Taian Electric Power Dispatching and Communication Centre， Taian 271000， China）

Abstract：? After the fault occurs in the distribution network， it is necessary to isolate the fault area， and restore the power supply to the non-fault area according to the current network structure and power flow distribution and satisfying the relevant constraints. In order to shorten the outage time and reduce the outage loss， and find the best power supply recovery scheme， this paper introduces elite bee colony algorithm and establishes the corresponding algorithm flow. The feasibility and superiority of this method are verified by comparing the actual distribution network fault recovery power supply cases of a city power supply company. The application effect of this method in practical application is counted and the economic benefits of this method are verified. It provides an important reference for the research of fault recovery methods of distribution network.

Key words： distribution network; fault recovery; elite bee colony