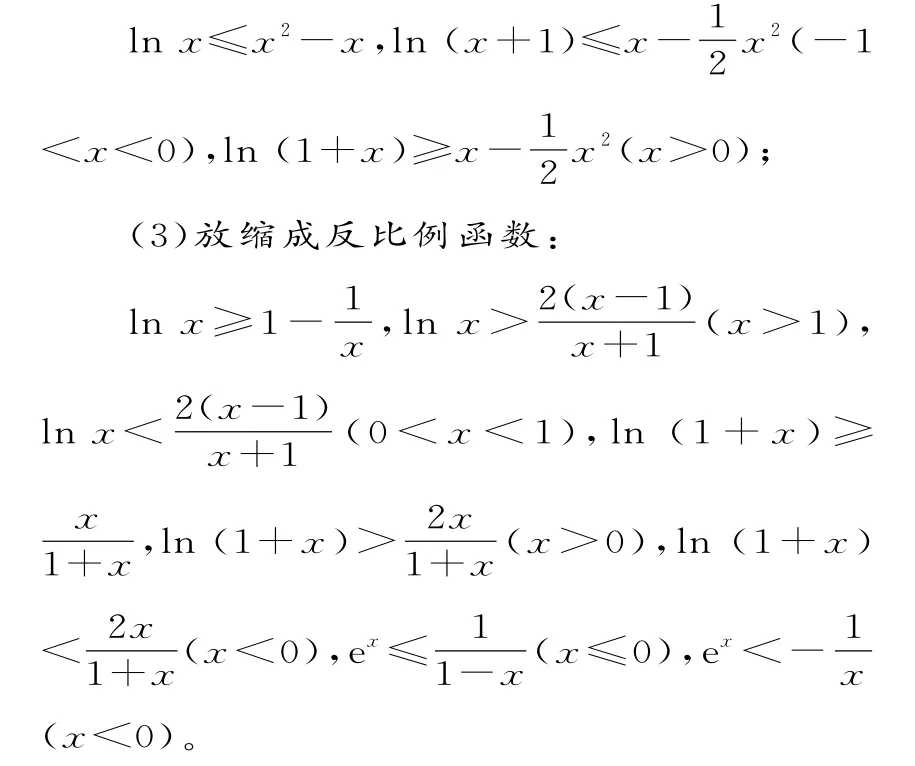求導后，該咋辦

■浙江省紹興市上虞區職教中心

縱觀近年來全國各地高考壓軸試題,導數解答題以對數函數、指數函數、反比例函數,以及一次函數、二次函數、高次函數中的兩個或三個為背景,組成一個具有鮮明特征的超越函數,研究該超越函數性質離不開其單調性,求導也自然成為同學們首要的操作步驟。實際上,我們遇到的函數比較復雜,同學們往往在求導后,不知所措? 下面介紹幾種通過求導來求解單調區間的方法,供同學們學習時參考。

一、分解因式

一般地,單調區間的求解過程：已知y=f(x),(1)分析y=f(x)的定義域;(2)求導數y'=f'(x);(3)解不等式f'(x)＞0,解集在對應區域內的部分為增區間;(4)解不等式f'(x)＜0,解集在對應區域內的部分為減區間。顯然,分解因式是求解代數不等式的有力武器。因此,對導函數分解因式是解這類題的首選。

例1(2019 年浙江省高考試題)已知實數a≠0,設函數x＞0,當時,求函數f(x)的單調區間。

分析：所給函數比較復雜,可先求出導函數,然后利用常規手段即分解因式解不等式f'(x)＞0或f'(x)＜0。

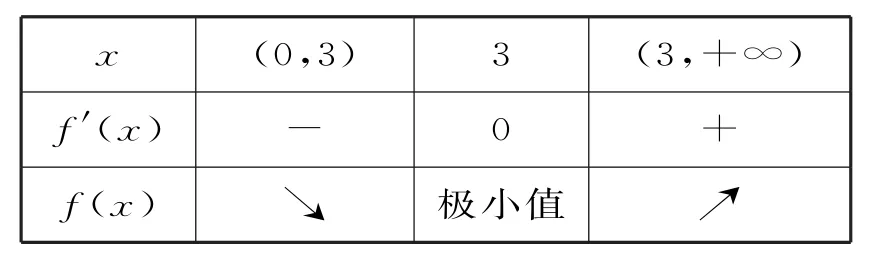
表1

所以,函數f(x)的單調遞減區間為(0,3),單調遞增區間為(3,+∞)。

點評：要順利求解復雜函數的單調區間,首先必須會準確求解函數的導數,其次要會熟練求解各類不等式：根式不等式、指數不等式、對數不等式。

二、分類討論

一般地,當導函數中含有參數時,可將問題轉化為求解含參不等式,需對參數進行分類討論。

例2(2019 年高考全國Ⅲ卷理數)已知函數f(x)=2x3-ax2+b。

(1)討論f(x)的單調性。

(2)是否存在a,b,使得f(x)在區間[0,1]的最小值為-1且最大值為1? 若存在,求出a,b的所有值;若不存在,說明理由。

分析：對函數f(x)=2x3-ax2+b求導,即得f'(x)=6x2-2ax=2x(3x-a),要確定f'(x)＞0,需對a分類討論。

解：(1)f'(x)=6x2-2ax=2x(3xa)。

令f'(x)=0,得x=0或

若a=0,f'(x)在(-∞,+∞)單調遞增。

(2)滿足題設條件的a,b存在。

(i)當a≤0時,由(1)知,f'(x)在[0,1]上單調遞增,所以f'(x)在區間[0,1]上的最小值為f(0)=b,最大值為f(1)=2-a+b。此時a,b滿足題設條件當且僅當b=-1,2-a+b=1,即a=0,b=-1。

(ii)當a≥3時,由(1)知,f'(x)在[0,1]上單調遞減,所以f'(x)在區間[0,1]上的最大值為f(0)=b,最小值為f(1)=2-a+b。此時a,b滿足題設條件當且僅當2-a+b=-1,b=1,即a=4,b=1。

(iii)當0＜a＜3 時,由(1)知,f'(x)在[0,1]上的最小值為,最大值為b或2-a+b。

綜上,當且僅當a=0,b=-1 或a=4,b=1時,f'(x)在[0,1]上的最小值為-1,最大值為1。

點評：分類討論是一種邏輯方法,是一種重要的數學思想,同時也是一種重要的解題策略,它體現了化整為零、積零為整的思想與歸類整理的方法。有關分類討論思想的數學問題具有明顯的邏輯性、綜合性、探索性,能訓練同學們思維的條理性和概括性。

三、零點法

當不等式f'(x)＞0為超越不等式時,可采用零點法即先觀察或求出導函數的零點,然后根據導函數的單調性寫出f'(x)＞0的解集即原函數的單調區間。

例3已知函數f(x)=ex-ln(x+m)。設x=0是f(x)的極值點,求m的值,并討論f(x)的單調性。

分析：根據x=0是f(x)的極值點確定m值,但發覺不等式f'(x)＞0 是超越不等式,即無法求解該不等式,需探究新的方法處理。

解：f'(x)=,由x=0是的極值點,得f'(0)=0,解得m=1。

于是f(x)=ex-ln(x+1),它的定義域為

點評：如果導函數存在零點,但令導函數為零后,出現超越方程,直接求解比較困難,此時可先用特殊值試探出方程的一個根,再通過研究其單調性說明其是唯一的。一般地,當導數式含有lnx時,可試根1,e或等,當導數式含有ex時,可試根1或0等。

四、二次求導

令導函數為零后,出現復雜超越方程,直接求解零點比較困難或能求出特殊零點但不清楚零點個數即確定不了導函數的單調性,可實施二次求導。

例4(2018 年高考全國Ⅲ卷理數改編)已知函數f(x)=(2+x+ax2)ln(1+x)-2x。若a=0,證明：當-1＜x＜0 時,f(x)＜0;當x＞0時,f(x)＞0。

分析：求導后,f'(x)=ln(1+x)-顯然f'(x)＞0為超越不等式,雖然可以觀察到函數f'(x)的零點,但函數f'(x)的單調性不確定,故需二次求導。

解：當a=0時,f(x)=(2+x)ln(1+x)-2x,f'(x)=ln(1+x)-

設函數g(x)=f'(x)=ln(1+x)-

當-1＜x＜0時,g'(x)＜0;

當x＞0時,g'(x)＞0。

故當x＞-1時,g(x)≥g(0)=0,從而f'(x)≥0,且僅當x=0時,f'(x)=0。所以f(x)在(-1,+∞)上單調遞增。

又f(0)=0,故當-1＜x＜0時,f(x)＜0;當x＞0時,f(x)＞0。

點評：當無法采用零點法時,可對導函數y=f'(x)再次求導,以期求出導數的零點及判斷單調性。此時,一定要清楚求導的目的,即利用導數的符號,判斷原函數的單調性。

五、設而不求

在解決解析幾何問題時,我們常常把題目中某些相關的點的坐標先設出來,但在解題中并不求出它的具體值,只把它作為解題過程中的“橋梁”,使問題快速獲解,這便是我們常說的“設而不求”的數學思想。在導函數中,我們如果能確定其零點存在,但又無法用顯性的代數式進行表達,即所謂的“隱零點”,則可采用形式上虛設,運算上代換的方法。

例5已知函數f(x)=x+xlnx。

(1)求函數f(x)的圖像在點(1,1)處的切線方程;

(2)若k∈Z,且k(x-1)＜f(x)對任意x＞1恒成立,求k的最大值。

分析：對于(1)直接按切線定義可得。對于(2),恒成立問題首先考慮分離參數,即則只需借助導數求出函數g(x)的最小值,但求導后發現,其導函數對應的方程為超越方程,無法求得極值點和單調區間,解題陷入困境。此時,若果斷設函數的極值點,則可“柳暗花明”,豁然開朗。

解：(1)因為f'(x)=lnx+2,所以f'(1)=2。

函數f(x)的圖像在點(1,1)處的切線方程y=2x-1。

(2)由(1)知,f(x)=x+xlnx,所以k(x-1)＜f(x)對任意x＞1恒成立,即k＜對任意x＞1恒成立。

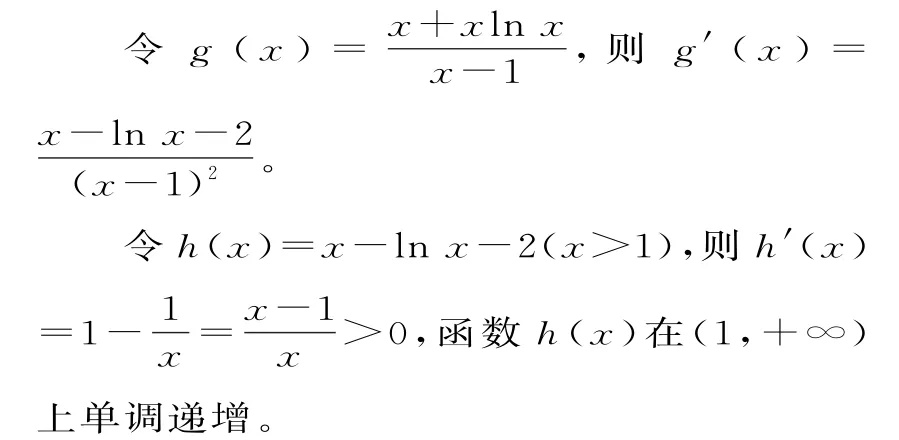
因為h(3)=1-ln 3＜0,h(4)=2-2ln 2＞0,所以方程h(x)=0 在(1,+∞)上存在唯一實根x0,且滿足x0∈(3,4)。

當1＜x＜x0時,h(x)＜0,即g'(x)＜0;當x＞x0時,h(x)＞0,即g'(x)＞0。所以函數在(1,x0)上單調遞減,在(x0,+∞)上單調遞增。

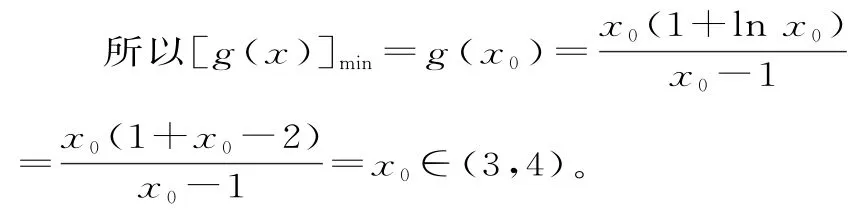
因此,k＜[g(x)]min=x0∈(3,4),整數k的最大值是3。

點評：當導函數存在零點,但零點式子非常煩瑣或無法求解時,可考慮虛設零點x0,再對f'(x0)=0 進行合理的變形與代換,將超越式化為普通式,從而達到化簡f(x0)的目的。

六、不等式放縮

眾所周知,如果能順利求解不等式f'(x)＞0(＜0),那么導函數的問題都可迎刃而解。因此,將復雜的超越不等式放縮為普通的代數不等式的方法應運而生。

例6設函數f(x)=ex-1-x-ax2。

(1)若a=0,求f(x)的單調區間;

(2)當x≥0時,f(x)≥0,求a的取值范圍。

分析：對于(1)直接求導可順利解得。對于(2),根據ex≥x+1 可得不等式f'(x)≥x-2ax=(1-2a)x,從而可知1-2a≥0,即時,f'(x)≥0,判斷出函數f(x)的單調性,得到答案。

解：(1)a=0 時,f(x)=ex-1-x,f'(x)=ex-1。當x∈(-∞,0)時,f'(x)＜0;當x∈(0,+∞)時,f'(x)＞0。故f(x)在(-∞,0)上單調遞減,f(x)在(0,+∞)單調遞增。

(2)f'(x)=ex-1-2ax,由(1)可知ex≥1+x當且僅當x=0時等號成立。

故f'(x)=ex-1-2ax≥x-2ax=(1-2a)x,從而當1-2a≥0,即時,f'(x)≥0(x≥0)。而f(0)=0,于是當x≥0時,f(x)≥0。由ex＞1+x(x≠0)可得e-x＞1-x(x≠0),從而當1-2a＜0,即時,f'(x)=ex-1-2ax＜ex-1+2a(e-x-1)=e-x(ex-1)(ex-2a)。

故當x∈(0,ln 2a)時,f'(x)＜0。而f(0)=0,于是當x∈(0,ln 2a)時,f(x)＜0。

綜上可得a的取值范圍為

點評：由于放縮過程并非等價變換,因此要注意放縮求解的格式。常用的放縮公式有：(1)放縮成一次函數：

lnx≤x-1,lnx＜x,ln (1+x)≤x,ex≥x+1,ex＞x,ex≥ex;

(2)放縮成二次函數：