楔形物垂向撞擊船體板的簡化解析法研究

張 敏， 劉敬喜， 趙 耀， 黃詩雯

(1. 武漢輕工大學 機械工程學院，武漢 430048； 2. 華中科技大學 船舶與海洋工程學院，武漢 430074； 3. 船舶與海洋水動力湖北省重點實驗室，武漢 430074； 4. 漢陽專用汽車研究所，武漢 430056)

船體外板和甲板受外物如跌落物、海底礁石、浮冰或其它船只的撞擊作用下，會發生大變形甚至破裂。受損船板會影響船體的整體強度，嚴重的會導致船體進水、燃油泄漏甚至人員傷亡。研究船體結構受外物撞擊的研究方法主要有：模型試驗法、數值仿真法和理論分析方法[1]。相對其它兩種方法，理論分析方法計算效率更高，因而在船舶耐撞性設計初期更實用。在理論分析模型中，通常將撞擊物簡化為球形體或楔形體，用來推導結構的抵抗變形能力[2]。

近年來，人們對船體板受外物撞擊的研究主要集中在球形物的撞擊上，并且研究出了一系列的解析解[3-7]。這些解的共性是考慮板在球頭作用下的膜拉伸作用，將板的變形作用當成軸對稱問題來求解。然而，矩形板受楔形頭作用下的變形模式與球頭作用下的不同。楔形體與外板接觸作用的部分只有頂端，因此可以看成矩形板受線載荷或矩形面載荷的作用。相關學者也做了一些研究，Cho等[8]提出了一套解析解，將板受撞頭壓載下所形成的塑性鉸劃分為不同的區域，考慮不同區域的膜拉伸作用和塑性鉸的彎曲作用，得到有限變形下的能量吸收值。孫斌等[9]基于楔形船艏撞擊整體船體舷側的場景，考慮外板變形區域的膜拉伸作用和變形區域周圍塑性鉸的彎曲作用，得到了傾斜楔形船艏撞擊船體板的抵抗力計算公式。船體加筋板在抵抗碰撞中，板是主要的吸能構件，準確預報板受撞擊下的變形抗力是十分必要的。然而，目前研究楔形體垂向撞擊光板的抵抗力計算公式比較少。

此外，船舶碰撞屬于低速碰撞問題，在結構短時間內的變形中，應變率會對材料起到強化作用，從而提高結構的抗力[10-11]。相對于低速碰撞，準靜態作用下的結構變形特征與低速碰撞下的類似[12]。而且在低速碰撞中，隨著撞擊體與被撞體質量比值的增大，準靜態作用下與低速沖擊下的響應會逐漸接近[13]。船舶碰撞中，撞擊體的質量一般比較大，被撞物為強構件約束下的板，其質量相對較小，因而在船舶碰撞中，準靜態分析下的結果與低速碰撞下的結果比較接近，且準靜態分析方法(試驗、數值仿真或解析法)相對來說會更方便。

因此，本文提出了一套船體板受楔形物體準靜態垂向作用下的簡化解析方法，得到了簡潔的抵抗力-撞深計算公式。通過模型試驗驗證了該解析解的準確性。本文提出的船體板遭受楔形物撞擊下的抵抗力的解析方法對船體外板的耐撞性設計及評估有一定的指導作用。

1 理論分析

圖1(a)是尺寸為2a0×2b0(a0和b0分別為矩形板的半長與半寬)的矩形板受尺寸為2a×2b(a和b分別為矩形撞頭的半長與半寬)的矩形面載荷作用下的變形模式，若b=0，即可認為是矩形板受線載荷作用。考慮矩形板板變形在Oxy直角坐標系下的對稱性，僅考慮第一象限的載荷響應。假設在撞擊過程中，外板中與撞頭接觸的部分是固定不變的。因此，第一象限的板由撞頭與矩形板的斜連接線劃分為兩部分，即：區域一和區域二。分別推導這兩部分的抵抗力，疊加即可得到矩形板受面載荷壓載下的整體抵抗力。

將變形區域一置于柱坐標系下計算。如圖1(b)所示，區域一上的每一點均可在以O1為原點，ρ，θ，w為坐標軸的柱坐標系中表示。

圖1 矩形板變形模式Fig.1 Deformation mode of the rectangular plate

考慮任意轉角θ下的線O1O3，線O1O3上任意一點的撓度可用線性表達式w(ρ)來表示

w=c1ρ+c2,ρmin≤ρ≤ρmax

(1)

式中：c1和c2為待確定常數；ρmin和ρmax可以表示為

ρmin=m/cosθ,ρmax=(b0-b+m)/cosθ

(2)

式中：m為點O1和點O2之間的間距，根據幾何關系，m可以求得

(3)

此外，θ的最大值α可以表示為

(4)

wmax是變形曲線上的最大值，因此，式(1)中常數c1和c2可以由如下邊界條件確定。

ρ=ρmin,w=wmax
ρ=ρmax,w=0

(5)

將式(2)、式(3)和式(5)代入式(1)，得到板的變形表達式

(6)

考慮板在壓載過程中的膜拉伸作用，拉伸應變ερ可以表示為

(7)

式中：u為板變形過程中的面內位移，板在側向受垂向壓載發生面外大變形時，一般可將其忽略。因此，拉伸應變的第一項為0。

結合式(6)，可以得到板的拉伸應變

(8)

在變形區域上積分求平均值，并結合式(2)～式(4)，得到區域一板在任意撓度下的平均應變值

(9)

求應變的一階導數，得到平均應變的應變率為

(10)

(11)

式中：σ0為板材的流動應力，可以通過板的屈服強度σy和抗拉強度σu的平均值求得；t為板厚；A1為區域一的初始面積。

根據上限定理，外力功的功率與結構應變能率相等

(12)

式中：P1為板區域一所貢獻的垂向抗力。

結合式(2)～式(4)和式(10)～式(12)，得到外力P1

(13)

區域一板所吸收的能量E1可以通過對撞深求積分得到

(14)

考慮材料的真實應力應變關系σeq(εeq)，可以得到更加準確的解析解，將等效應力σeq替代式(13)和式(14)中的流動應力σ0，可以得到

(15)

(16)

此外，板區域二變形所對應的抗力的求解過程與區域一相同。因此可以求得所對應的抗力P2，所吸收的能量E2和該區域的平均應變ερ2avg。其表達式為

(17)

(18)

(19)

矩形板整體的變形抗力P和變形吸能E可以通過疊加各區域的抗力得到。其表達式為

P=4(P1+P2)

(20)

E=4(E1+E2)

(21)

2 試驗驗證

為了證明所提解析解的準確性，開展了矩形板受楔形頭的準靜態壓載試驗，試驗工裝如圖2所示。光板試件由上下夾具夾緊并由兩排高強螺栓固定，光板變形區域的尺寸為400 mm×600 mm，試驗中同步采集板的變形抗力及撞頭行進的位移，采集頻率為100 Hz。其中，力傳感器最大量程為20 t，精度為0.1%；位移傳感器最大量程為750 mm，分辨率為0.05 mm。基于兩種形狀的撞頭開展了4組試驗，試驗工況如表1所示，400 mm×600 mm矩形板分別受尖頭(頂端長160 mm)和平頭(頂面尺寸160 mm×80 mm)側向壓載。另外，試驗完成后用相機記錄了兩組試件(試件S1_1和試件S1_2)的三維變形形式。

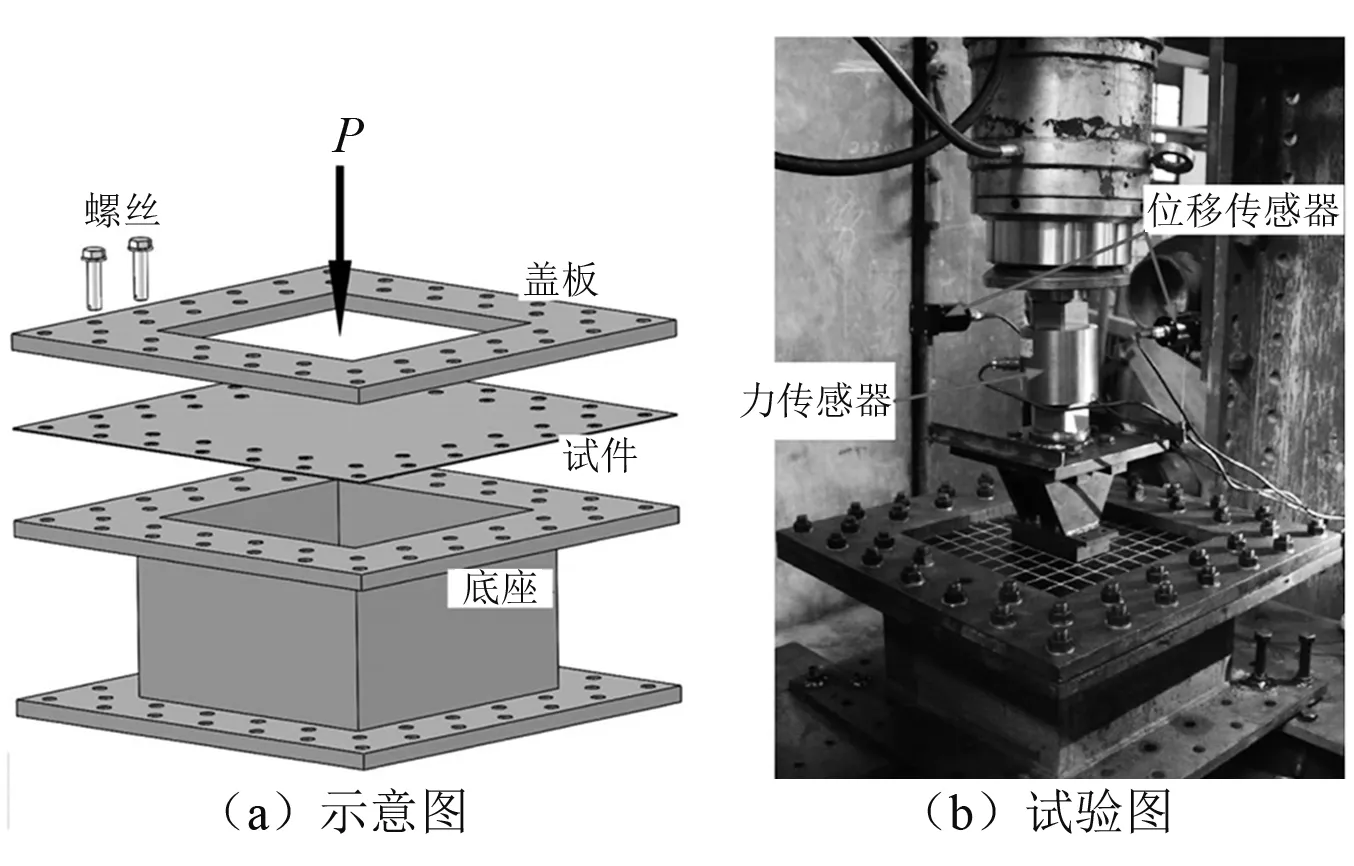
圖2 準靜態壓載試驗工裝Fig.2 Experimental set-up for quasi-static indentation test

表1 試驗工況

試驗中所用板材為1.455 mm厚的冷板，通過拉伸試驗得到了板的材料曲線，其工程應力-應變曲線如圖3所示，得到的材料參數匯總在表2中。此外，板材的真實應力應變可由如下關系式得到

σt=σe(εe+1)

(22)

εt=ln(εe+1)

(23)

式中：σe和εe分別為材料的工程應力和工程應變；σt和εt分別為材料的真實應力和真實應變。

然后將板屈服后、材頸縮前計算得到的真實應力應變值用函數關系式表達，以用于解析解表達式中。圖3中也給出了材料的真實應力-應變關系，其關系用Voce公式[14]表達為

σeq=σy+R0·εeq+R∞(1-e-nεeq)

(24)

Voce公式中的材料參數R0，R∞，和n可通過曲線擬合得到，其值分別為：383.6 MPa, 95.89 MPa和22.08 MPa。

圖3 試驗板材材料曲線Fig.3 Material relations of the plate

表2 材料參數

3 結果對比

一般來說，在碰撞力的解析預報中，等效應力解考慮了結構在變形過程中應力隨變形量的變化，因此，預報結果會比用流動應力計算的剛塑性解更準確。然而，由于在板材出廠時會直接給出材料的屈服強度σy和抗拉強度σu，可直接求得流動應力σ0，因此，剛塑性解在實際工程應用中會更方便。故本章將等效應力解和剛塑性解與試驗值對比，檢驗解析解的準確性。

解析解與試驗結果對比如圖4所示。四種工況下的等效應力解均與試驗結果吻合較好，而在矩形板受尖頭作用的工況中，剛塑性解比試驗結果大。圖5為試件在尖頭和平頭作用下的最終變形圖，從圖5可知，尖頭作用下的矩形板側向變形所形成的輪廓(即圖中的側視圖)曲率變化比平頭作用下的要大，尤其是撞頭附近的變形梯度更大，說明矩形板受尖頭作用下的局部變形較大，這是導致實驗測得的抵抗力比剛塑性解要小的原因。

圖4 抵抗力-撞深曲線比較Fig.4 Comparison of resistance-penetration curves

圖5 試件三維變形圖Fig.5 Three-dimensional deformation of the specimens

比較矩形板受尖頭和平頭作用下的載荷響應曲線，尖頭作用下的載荷曲線初始階段上升較后期要緩慢。這個過程中，板材主要發生局部變形；隨后，載荷曲線上升較迅速，說明試件在發生整體變形，同時試件發生整體變形所對應的載荷曲線與剛塑性解曲線幾乎平行，這和解析解推導中假設矩形板只發生整體變形是一致的。而板在平頭的作用下，沒有發生載荷曲線在初始階段上升緩慢的現象，因此其局部變形很小。因此，剛塑性解能很好地預報矩形板受平頭壓載時的抗力。

4 結 論

本文提出了船體板受楔形物垂向撞擊下發生大的塑性變形的抵抗力解析計算方法。通過與試驗結果對比，得到了以下結論：

(1) 相對于平頭作用下的矩形板，尖頭作用下的矩形板在初始階段會發生局部變形，產生較小的抗力。

(2) 解析法中，等效應力解可以比較好地預報板整個變形過程的抗力，包括局部變形和整體變形。而剛塑性解只能預報板整體變形的抗力。

(3) 本文提出的簡化解析解公式簡便，有較高的計算精度，適用于船體板受楔形物撞擊下的耐撞性計算，對船體結構的耐撞性設計有較好的指導意義。