一種快速收斂的流水線型ADC數字校正方法

宮月紅，卞良浩，張少君，王明雨

（山東交通學院船舶與輪機工程學院，威海264209）

1 引 言

在現代通信系統中，模數轉換器（ADC）做為數字部分與模擬部分的接口，占有舉足輕重的地位。隨著數字信號處理技術的發展，對模數轉換器速度和分辨率的要求越來越高。在幾種常用結構的模數轉換器中，流水線型ADC 以其中高速度與中高分辨率而得到廣大用戶的青睞。隨著性能的提高，流水線型ADC 面臨的主要問題是越來越高的功耗[1-2]。為了降低流水線型ADC 的功耗，提高線性度，研究者們提出了一系列的設計方法。在文獻[3]中，采用開環放大器作為第一級級間余量放大器，而對于開環放大器引入的非線性誤差，采用基于統計規律的數字校正技術來校正。基于統計的數字校正技術存在的問題是算法收斂過程依賴統計規律，收斂時間過長。與基于統計規律的數字校正技術對應的是確定性的校正技術，這類校正技術算法收斂不依賴統計規律，收斂速度快。在文獻[4-5]中，設計了專門的參考ADC 法來加速收斂，但是參考ADC 需要增加額外的模擬電路硬件開銷，這在數字電路比例日益增大的細線工藝下是不經濟的。在文獻[6-7]中，采用加入測試信號的方法加速收斂，但是選擇的傳輸函數與實際放大器傳輸函數相差較多，校正精度有待提高。

基于上述背景，在此設計一款12 位、40MHz 的流水線型ADC。為了降低系統功耗，采用開環放大器作為第一級級間余量放大器。為了校正級間余量放大器引入的非線性誤差，提出一種確定性的數字校正方法。在這種校正方法中，通過加入測試信號的方式建立后級ADC 傳輸函數模型，通過傳輸函數模型來估計理想的輸入碼值，對非線性誤差進行校正。選用更接近于實際情況的三次多項式模型做為級間放大器傳輸函數模型，從而提高校正精度。系統工作流程分為測試模式和正常轉換模式。系統在測試模式下輸入測試信號，建立傳輸函數模型；在正常轉換模式下，采用建立的傳輸函數模型來估計理想輸入信號碼值，實現校正。通過測試信號的加入，可以使系統快速收斂。

2 MDAC 誤差模型

傳統的流水線型ADC 由采樣保持電路、子ADC、MDAC、時鐘對齊電路等組成。圖1 以單端工作模式為例給出了其中1.5 位MDAC 的示意圖。

圖1 MDAC 工作原理示意圖

圖1(a)中的級間余量放大器采用開環放大器；圖1(b)采用電荷轉移式的閉環放大器結構；圖1(c)采用電容翻轉式的閉環放大器結構。圖中，Φ1 和Φ2 為一對兩相不交疊時鐘，用以控制開關1 和開關2；Vin為輸入信號，VDASC為本級子ADC 輸出碼值對應的輸入電壓值；Cin、Cf和Cp分別為采樣電容、保持電容、寄生電容。在圖1(a)中，當開關1 關閉時，Cin被充電。當開關2 閉合時，Cin上的電荷發生移動，放大器輸入端的電壓得到確定，由開環放大器放大，增益由開環增益決定。在圖1(b)中，當開關1 關閉時，Cin被充電。當開關2 閉合時，一部分Cin上的電荷轉移到Cf上，確定放大器輸入端的電壓并放大，增益由Cin與Cf的比值決定。在圖1(c)中，當開關1 關閉時，Cin和Cf同時充電。當開關2 閉合時，一部分Cin上的電荷轉移到Cf上，實現放大，增益由Cin與Cf的比值決定。

由上述分析可見，采用開環放大器作為級間余量放大器，級間增益取決于開環放大器增益，所以，放大器的傳輸函數即為開環放大器的傳輸函數。開環放大器的傳輸函數可以表示為如下多項式形式：

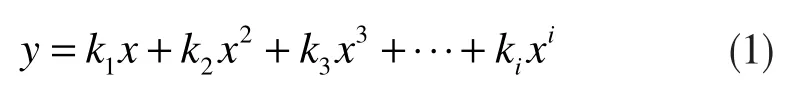
由參考文獻[8]可知，通過電路設計技巧，可以控制式(1)中三階以上的誤差小于某個數量級，相對于ADC 的精度可以忽略的程度。而式(1)中的偶次項可以通過差分結構消除，所以式(1)可以簡化為如下形式：

3 校正結構

3.1 函數模型創建

在流水線型ADC 中，子級誤差對系統的影響從第一級到最后一級逐級減小，所以第一級誤差對整體的影響是最大的。在此，為了驗證算法，簡化電路，僅對第一級級間余量放大器誤差進行校正。圖2 給出了校正系統的結構框圖。

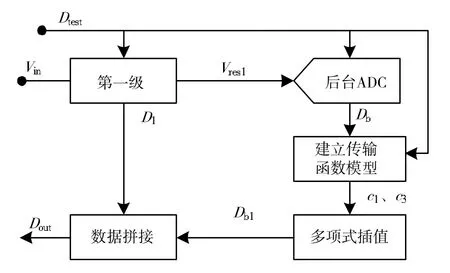
圖2 校正系統結構框圖

該系統由第一級3.5 位子ADC 和后臺ADC 兩部分構成，第一級級間余量放大器采用開環結構。對于開環放大器引入的非線性誤差，采用后臺校正方式校正。校正過程中，將除第一級以外的其他子級看為一個整體，對應的輸出碼值稱為后臺碼值。

為了對第一級級間余量放大器誤差進行校正，需要建立放大器傳輸函數模型，并應用該模型校正放大器的非線性誤差。系統工作分為測試模式和正常轉換模式兩個階段，分別由兩組時鐘控制。在測試模式下，系統輸入測試信號，用于建立放大器傳輸函數模型；在正常轉換模式下，通過建立的傳輸函數模型來估計理想的輸入碼值，最后的輸出通過將估計所得的理想碼值與第一級輸出碼值拼接得到。

可將開環放大器傳輸函數模型構建為三次多項式的形式，如下式：

此處，有一點不同的是，式(1)中放大器的輸出y為輸入x 的函數。在此，因為需要通過輸出碼值估計輸入值，為了簡化運算，將輸入x 表示為輸出y 的函數。

3.2 算法工作原理

系統工作分為測試模式和正常轉換模式兩個階段，傳輸函數模型建立過程在測試模式下完成。為了求解式(3)中三次多項式中的參數c1和c3，需要由測試信號提供三組已知點信息。當測試信號進入系統后，系統校正機制開始工作。多項式中參數通過矩陣運算求得。假設測試信號提供的三組已知點信息分別為(x0，y0)、(x1，y1)、(x2，y2)，將這三組數據分別代入式(3)，可得到如下方程組：

式(4)也可以表示為如下矩陣形式：

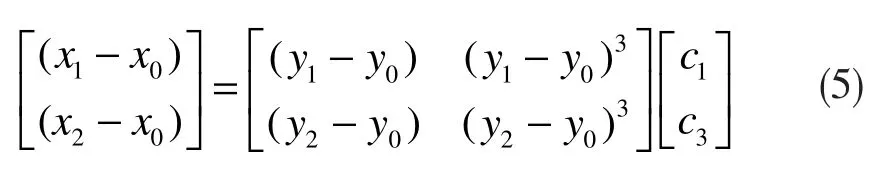
為了求得c1和c3的數值，需要通過矩陣運算對方程組進行求解，矩陣運算過程如下式：

通過式(6)中的矩陣運算，可以求得傳輸函數中一階和三階參數值，從而建立傳輸函數方程。在正常轉換模式下，應用建立的傳輸函數方程，就可以通過多項式插值，由后臺碼值估計理想的輸入碼值，實現校正。

3.3 算法收斂與硬件開銷

以上提出的校正方法屬于確定性的校正算法，傳輸函數建立是在測試信號的輔助之下完成的，所以該算法收斂不依賴統計規律，收斂速度快。在測試模式下，系統輸入測試信號，建立傳輸函數模型；在正常轉換模式下，應用傳輸函數模型進行多項式插值來估計理想輸入碼值實現校正。其中傳輸函數模型建立、多項式插值等大部分流程都通過數字電路完成，而數字電路的速度遠遠高于模擬部分電路，所以校正過程能夠在一個時鐘周期之內完成。

校正過程中的硬件開銷集中發生在建立傳輸函數模型時的矩陣運算以及估計理想輸入碼值時的多項式插值等步驟中。

4 仿真結果

為了對數字校正方法進行校正，設計一款12位、40MHz 的流水線型ADC。在Cadence 仿真環境下， 采用Spectra 數模混合仿真工具對校正系統進行仿真。采用0.18μm CMOS 工藝，電源電壓為3.3V。圖3 給出了系統動態仿真結果。選取輸入信號的頻率在奈奎斯特頻率附近，信號頻率為19MHz。由圖可見，校正前系統SFDR 為60.4dB，計算得出對應的SNDR 為49.8dB；校正后SFDR 為86.7dB，計算得出對應的SNDR 為72.8dB。可見，經過校正，系統的線性度得到明顯提高。

圖3 校正前后動態特性仿真結果

仿真的數字校正部分通過Verilog 語言描述，在Cadence 仿真環境下進行邏輯綜合、估計功耗，得到系統校正過程中數字部分的硬件開銷、功耗及收斂時間信息，詳細結果如下：

硬件開銷：約為8400 個邏輯門；

功耗：約為22mW；

收斂時間：約為4096 次采樣時間。

5 結 束 語

細線工藝下，晶體管本證增益與電源電壓的降低，使得高性能放大器的設計越來越困難，采用數字提高技術來增強數模混合電路系統的性能已成為一種流行的設計趨勢。為了降低流水線型ADC 系統功耗，采用開環放大器作為流水線型ADC 級間余量放大器，為了校正開環放大器引入的非線性誤差，采用一種確定性的數字校正技術進行校正。為了建立傳輸函數模型，在測試周期，在輸入端輸入測試信號，通過矩陣運算計算傳輸函數參數，從而對非線性誤差進行校正。仿真結果表明，該校正算法能有效地提高系統的線性度。測試信號的使用有效縮短了算法收斂時間，提高了校正精度。