基于Lanchester方程的反艦作戰效能評估方法

李海濤

(中國人民解放軍91404部隊43分隊， 秦皇島 066000)

0 引言

各國軍方對裝備作戰效能評估方法和理論研究工作高度重視,積極探索創新,裝備作戰效能評估被廣泛應用于新裝備的研制開發、新戰術戰法的評估和裝備模擬訓練等領域,有效地促進武器裝備的更新換代，推動了軍事理論創新與發展，提升了部隊戰斗力[1]。

美軍早在上個世紀60年代就開始研究武器裝備系統的作戰效能評估問題，評估的理論和方法日趨成熟，建立了較為完備的裝備作戰效能評估體系，在武器裝備、作戰研究和部隊訓練等領域被廣泛應用，取得了良好的軍事經濟效益[2]。美軍在裝備作戰效能評估方面取得的成功經驗為個國軍事人員所重視，其關于作戰效能評估的理論與方法也為各國開展相關領域的研究提供了借鑒[3]。

1 反艦作戰效能評估方法分析

現在反艦作戰主要武器是反艦戰術導彈，因此主要評估反艦導彈的作戰效能。在反艦導彈武器系統效能評估中，無論是導彈武器系統的引導過程，還是水面艦艇反艦作戰的對抗過程，均屬于隨機過程[4]。一般討論的隨機模型是根據反艦導彈武器系統具有的包含大量隨機因素的規律，以概率論為基本數學工具，結合隨機過程理論、模糊數學理論、人工智能理論、灰色系統理論和人工神經網絡理論建立的，其結果通常也是在概率意義下表示出來的[5]。到目前為止，對武器系統作戰效能進行評估的隨機方法通常可分為統計試驗法和解析法兩大類[6]。

統計試驗法具有通用性強、沒有原理誤差、以及精度結果可以預測和控制等優點。但是為統計出可信的計算結果它需要樣本量較大，且獲取這些樣本的試驗過程耗時較長。這樣，在導彈武器系統這種對實時性、快速性要求較高的環境中，使用難度比較大[7]。

比較傳統的解析法如英國人F.W.Lanchester建立的描述作戰動態過程的Lanchester微分方程[8]。在該方程的基礎上，W.PHannah和J.Tavantzis等人先后引入了作戰過程的隨機因素，建立了多種形式的隨機類型Lanchester方程。另外，排隊論，或稱隨機服務系統理論也是解析分析導彈武器系統效能進行評估的較為有效的工具。下面，重點討論集中對導彈武器系統效能進行評估的較為成熟的解析法，即隨機類型的Lanchester方程分析法、協方差分析描述函數技術和統計線性化伴隨法[9]。

英國人F.W. Lanchester首先建立了描述作戰動態過程的微分方程，并且該理論不斷完善。利用該理論建立反艦導彈-艦艇防控火力對抗的確定型Lanchester模型，并以此到處隨機類型的Lanchester方程[10]。

2 確定型Lanchester方程評估方法

在反艦導彈與水面艦艇反導火力系統的攻擊與防御抗擊的隨機過程中，艦艇受損情況與單位面積上的艦載反導火力單元數量和攻擊的導彈數量相關[11]，因此推導水面艦艇反艦作戰的損耗方程時可做以下假設：

(1) 水面艦艇受損情況可近似符合Lanchester第二線性定律；

(2) 反艦導彈以Poisson分布隨機地到達水面艦艇后，只攻擊艦艇主體區域，艦載反導火力單元未受到毀傷；

(3) 水面艦艇艦載反導火控雷達對導彈的發現時間及火力單元單次設計時間均服從負指數分布，設分布參數為ξ，防控火力單元兩次發射間隔時間期望為τ。

取b(t)為來襲的反艦導彈數量；r(t)為艦載反導火力單元數。則可得到艦載反導火力系統在τ時間內未發現任何來襲目標的概率為式(1)。

P0(τ)=e-ξτ

(1)

則在τ時間內b(t)個目標至少被發現一個的概率為式(2)。

P1(τ)=1-e-ξτb(t)

(2)

發現并擊毀一枚導彈的概率為式(3)。

P=Pk·P1(τ)=Pk[1-e-ξτb(t)]

(3)

式中，Pk為反導火力系統 的單發殺傷概率。

τ時間內r(t)個反導火力單元殺傷來襲導彈的期望值為式(4)

E(b)=r(t)Pk[1-e-ξτb(t)]

(4)

反艦導彈是以參數為λ的Poisson分布隨機來襲，假設t時刻導彈能夠突防的概率為Pt，λpt則為導彈到達水面艦艇反導火力單元防御區域時的飛行速度，來襲導彈在反導火力單元防御區域數量變化可做如下推導，如式(5)[12]。

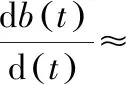
(5)

取AR為水面艦艇反導火力單元防御區域的總面積，rv為單個反導火力單元防御區域的半徑，rk為單枚反艦導彈的有效毀傷區域的半徑。水面艦艇若有r(t)個反導火力單元，一枚反艦導彈對該系統火力單元的殺傷概率為式(6)。

(6)

反艦導彈到達率為λ，則反導火力系統在b(t)枚導彈攻擊下的損耗率為式(7)。

(7)

式(1)和式(2)即為水面艦艇反艦作戰時攻防對抗系統的確定型Lanchester方程。

3 隨機型Lanchester方程評估方法

在反艦作戰過程中，設B(t)為t時刻反艦導彈數量的隨機函數，設R(t)為t時刻水面艦艇火力單元數的隨機函數，可得出反艦作戰時攻防概率分布函數為式(8)[13-17]。

pb,r(t)=p[B(t)=b,R(t)=r]

(8)

對反艦作戰過程進行分析得出，t+Δt時刻pb,r(t)動態方程為下述各獨立事件的概率之和：

(1)t時刻處于狀態(b+1,r)，在Δt時間內有一枚導彈被攔截或飛離火力殺傷區，該事件的概率為式(9)。

pb+1,r(t)=[Pk·ξ·r·(b+1)+λ·pt]Δt

(9)

(2)t時刻處于狀態(b+1,r)，在Δt時間內有一枚導彈飛入火力殺傷區，該事件的概率為式(10)。

pb+1,r(t)=λΔt

(10)

(3)t時刻處于狀態(b,r+1)，在Δt時間內有一個火力單元被擊毀，該事件的概率為式(11)

(11)

(4)t時刻處于狀態(b,r)，在Δt時間內沒有導彈火力單元的數量變化，該事件的概率為式(12)

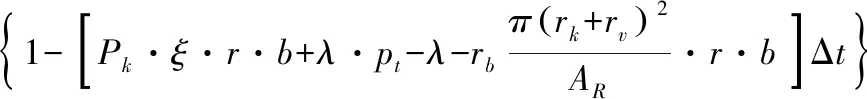
(12)

上述4式相加求導即可得到狀態概率的動態方程，即基于Lanchester隨機類型方程的反艦作戰攻防對抗評估方程。針對該方程求解可得到任意時刻t對抗雙方評估要素的概率pb,r(t)，對各要素進一步分析可得到任意時刻t水面艦艇反艦作戰效能。下式即為在t時刻導彈能夠突破防御火力系統的概率為式(13)[18]。

(13)

4 反艦作戰效能評估方法

根據隨機型Lanchester方程評估方法，可以推導出反艦導彈突防時作戰效能評估方法，即反艦作戰效能評估方法。推導步驟如下：

(1) 假設第一枚反艦導彈進入水面艦艇的反導火力范圍是為作戰起始時間，則反艦作戰攻防對抗的初始狀態則為：b(0)=1，r(0)=n；其中n為水面艦艇火力單元個數；隨機型Lanchester方程初始值則為式(14)[19]。

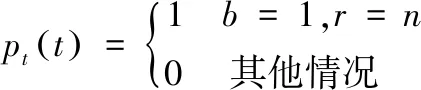
(14)

(2) 依據突防導彈數量及水面艦艇的反導火力單元數量排列組合，利用隨機型Lanchester方程可得出不同導彈和反導火力單元數量情況下的反艦作戰突防概率[20]。

(3) 根據隨機型Lanchester方程可推導出突防概率分布函數pb,r(t)；對該函數求解可得出任意時刻t水面艦艇的反艦作戰效能[21]。

5 總結

海戰場是未來戰爭的主戰場，水面艦艇是海軍部隊遂行海上作戰任務的重要作戰單元[22]。實踐表明，做好反艦作戰效能評估的研究，不僅可以減少作戰訓練經費、調高效率，而且對于加強海軍裝備建設、提高海軍部隊戰斗力具有極為重要的意義[23]。