基于優化免疫算法冷鏈物流配送路徑研究

施文嘉, 邵竑湄, 唐迪, 胡書紅

(國網浙江省電力有限公司 電力科學研究院, 杭州 310000)

0 引言

國內外許多研究學者就冷鏈物流配送路徑的優化進行了廣泛關注[1-4]，其中的要點與難點就在于車輛路徑的合理選擇問題。很多研究學者提出通過算法來解決這一問題，其中精確算法無法解決大規模車輛配送路徑的選擇處理問題，只善于求解小規模車輛問題[5]；后來提出的啟發式算法[6]很好的解決了這一難題，但是又出現了收斂速度慢，易早熟等問題；為克服這一缺陷，通過對算法進行改進提出了遺傳學算法，但是遺傳學算法在解決車輛配送路徑優化問題上存在效率低下的情況[7]。基于以上考慮，本文提出了基于優化免疫算法來解決冷鏈物流配送路徑優化問題。該算法使用廣泛，操作便捷，實用性強，結合城市路網，構建冷鏈物流配送總成本最小數學模型，同時，對冷鏈物流配送路徑優化問題進行建模研究。

1 冷鏈物流配送路徑模型

生鮮產品在物流配送過程中，80%的損耗都是發生在運輸配送環節。從節約成本的角度出發，優化配送路徑是降低冷鏈物流成本的突破口。在配送過程中一是有車輛油耗，二是有區別普通常溫配送的能源消耗。另外一方面，時間是影響貨物新鮮程度的最關鍵指標，相比于普通常溫配送，冷鏈物流由于產品本身具有的易腐性特點使得對冷鏈物流配送中的時間窗要求更為嚴格，這樣也就造成了產生懲罰成本的幾率大大增加。

1.1 問題描述

冷鏈物流配送路徑優化問題可以描述為：

1) 配送中心以及客戶的地理位置已知，配送中心有多輛車，且每輛車都配有冷凍、冷藏設備。

2) 從配送中心出發，用m輛車向n個客戶進行貨物配送，客戶到配送中心的距離為d0j(j=1,2,…,n),客戶之間的距離為dij(i,j=1,2,…,n)。每輛車的額定載荷是已知的，為wi(i=1,2,…,m)，客戶對貨物的需求量是確定的，為ci(i=1,2,…,n)，并且ci≤wi。

3) 根據客戶的要求以及時間安排合理安排車輛進行貨物配送，使配送總成本最小。

1.2 模型假設以及約束條件

在對實際問題進行解決的過程中，有一些條件無法同時滿足，為簡化問題的處理描述，需要在進行數學模型構建前進行一些條件假設與約束。

模型假設：

1) 配送中心只有一個；

2) 一個配送中心可以同時為多個客戶提供服務，且貨物能夠滿足所有客戶的需求，同時配送中心的運輸能力足以調配；

3) 車輛的自重不應超過其額定載荷；

4) 車輛的最大行駛距離是確定的;

5) 在運輸過程中車內溫度保持不變，同時車輛在行駛過程中及打開車門時的貨損系數固定。

分配方案必須符合以下基本約束條件：

1) 在每個分配路徑上，所有客戶的總需求不超過分配車輛的額定負載；

2) 配送路徑的長度不超過分配車輛的最大行駛里程；

3) 每個客戶的貨物由一輛配送車進行配送服務;

4) 對每個客戶的配送時間都必須在約定的時間窗內。

1.3 數學模型

冷鏈物流配送總成本包括固定成本、運輸成本、運輸過程中的貨損成本、開車門的貨損成本、冷鏈配送懲罰成本以及制冷成本。

為了構建數學模型，假設zp是由第p輛車服務的客戶數；使用集合Sp來表示第p輛車的路線，其中元素spi表示客戶i在第p輛車配送路線中的順序，sp0=0作為配送中心。

1) 包括折舊費，人工費等配送車輛的固定成本為式(1)。

C1=mf

(1)

其中，f是指每輛車的固定成本。

2) 與車輛的行駛的總路程成正比的運輸成本為式(2)—式(8)。

(2)

約束條件：

(3)

0≤zp≤np=1,2,…,m

(4)

(5)

Sp={spi|spi∈{1,2,…,n}i=1,2,…,zp}

(6)

Sp1∩Sp2=? ?p1≠p2

(7)

其中，

(8)

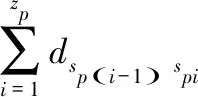
3) 即使運輸過程中保持低溫環境，依舊會造成生鮮產品一定的變質損耗。運輸過程中的貨損成本為式(9)。

(9)

其中，a為運輸過程中的貨損系數，g為貨物的價格，vip為0,1 變量，若第p輛車為i客戶提高服務，則vip=1，否則vip=0。

4) 打開車輛車門時，車內冷空氣會和外界熱空氣進行交換對流，造成車內溫度升高，造成生鮮損耗。開車門的貨損成本為式(10)。

(10)

其中，b為打開車門的貨損系數，Ri為每個客戶的貨物需求量。

5) 冷鏈配送懲罰成本

客戶對時間有一個要求的到達時間窗[mi,ni]，還有一個可接受的時間窗[Mi,Ni]，[mi,ni]?[Mi,Ni]；當到達客戶i的時間ti早于Mi，則需等待到Mi才能完成配送，這期間產生的貨損該系數仍然為a；當到達客戶i的時間ti在Mi與ni之間，則不需要懲罰。當到達客戶i的時間ti在ni與Ni之間，則需付出一定的懲罰成本，懲罰系數為β。當到達客戶i的時間ti晚于Ni，則提供服務不成功，懲罰成本為該客戶需求貨物的總價格。冷鏈配送懲罰成本的表達式為式(11)。

(11)

6) 制冷成本為式(12)。

(12)

其中，pf為制冷劑單價，F為制冷劑消耗量，tsp(i-1)spi為第p輛車從客戶(i-1) 到客戶i所用的時間。

綜上，冷鏈物流配送總成本最小數學模型表示如式(13)。

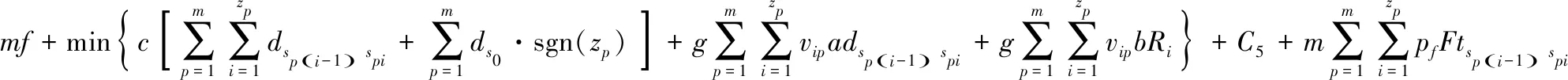
(13)

2 免疫算法模型理論

2.1 免疫算法原理

免疫算法是模擬生物免疫系統抗原抗體而生成的一種新型智能計算方法。免疫系統由抗原識別系統、記憶系統、抗體的加速和控制機制等組成，通過細胞分裂產生大量的抗體來抵抗各種抗原。免疫系統有很強的學習能力、識別能力及記憶能力，能夠辨別外界的有害信息，保證系統的安全穩定性。并且免疫系統具有保持群體多樣性的特點，因此免疫優化算法能夠有效克服在尋求最優解的過程中出現的“早熟”問題[8]，從而獲得全局最優解。

免疫算法流程圖如圖1所示。

實現步驟如下所示：

1) 分析問題。本文的研究目的是合理地確定配送車輛與客戶之間的關系，在滿足客戶需求、車輛載荷、時間窗等的約束條件下，求出最低總成本。

2) 抗原識別。本文將采用抗體與抗原之間的親和力大小來進行識別。

3) 產生初始抗體群。以隨機產生的抗體及記憶庫存儲的抗體作為初始抗體群。

4) 抗體評價。本文將對每個抗體進行評價。

5) 形成父代種群。按照個體期望繁殖概率進行排序，排名靠前的N個個體將被選作父代種群，并選取其中的m個放入記憶庫。

6) 判斷結束與否。滿足條件結束，否則進行下一步。

7) 新種群的產生。新種群由兩部分構成，父代選擇、交叉、變異等操作形成一部分，再從記憶庫中取出來形成另一部分。

8) 新一代種群形成之后進行循環操作。

2.2 優化算法操作流程

在免疫算法對配送總成本最低的求解過程中，以目標函數和約束條件為抗原，以其濃度為抗體。在免疫過程中，一些抗體作為記憶細胞被保留下來，當同源抗原再次攻擊時，記憶細胞會迅速爆炸產生大量抗體，產生更快的響應。同時，免疫系統具有自我調節功能，能維持抗體的多樣性和免疫系統的平衡[9]。

算法操作流程如下：

1) 抗原輸入和抗體編碼。

輸入抗原：目標函數和約束條件。

為方便研究，減少無效解的產生，采用自然整數進行編碼，形成抗體序列碼。對n個客戶進行編號，則路線可形成長度為n的抗體。如n=6,則抗體為(2，4，6，5，3，1)，此抗體序列碼即表示，從配送中心0出發，依次配送客戶2→4→6→5→3→1后，返回配送中心0，形成一條配送路徑。

2) 初始抗體群的產生

首次選擇時，抗體隨機選擇。之后，部分初始抗體通過免疫系統的記憶功能從記憶庫中獲得，其余部分再由系統隨機生成[10]。由于記憶庫中的抗體具有較高的適應度和較好的物種分布，因此可以提高收斂速度。

3) 親和度的計算

抗體與抗原間的親和度表示抗體對抗原的識別程度，當抗體遇到抗原時，它們越親和，那就越接近最優解。本文的親和力函數表示為式(14)。

(8)

其中Yi為冷鏈物流配送路徑優化的目標函數。

這樣就將最小值問題轉化為目標函數的最大值問題。

抗體與抗體間的親和度代表抗體之間的相似程度，抗體間的親和度表示為式(15)。

(15)

其中si,s表示兩個抗體間相同的位數，L表示抗體的長度。L的長度由配送的客戶的數量決定，如兩個抗體分別為(1，6，5，3，2，4)和(4，7，6，5，8，9)，兩個抗體有3個相同位數，則親和度為0.5。

4) 抗體濃度的計算

抗體濃度代表相似抗體在整個種群中所占的比例。當抗原或者新抗體攻擊免疫系統時，免疫系統將產生激烈反應，產生大量抗體。隨著抗體的增加，其親和力就會上升。達到一定程度時，其濃度就會降低[11]。即在優化過程中，會導致優化停滯，并收斂過早。

抗體濃度表示為式(16)。

(10)

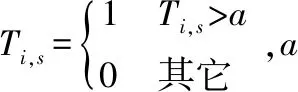
5) 期望繁殖概率：促進和抑制抗體產生

期望繁殖概率由抗體與抗原之間的親和度及抗體濃度來表示，期望繁殖概率Pi表示為式(7)。

(17)

從上式可以看出個體適應度與期望繁殖概率成正比，個體濃度與期望繁殖概率成反比。這樣就既可以鼓勵高適應度的個體的產生，又可以抑制高濃度個體的產生，從而保證個體的多樣性。

6) 交叉變異操作

群體更新的方法與遺傳算法基本相同。本文采用輪盤賭選擇機制進行選擇操作，個體期望繁殖概率即個體被選擇概率。采用多點交叉的方式進行交叉操作，從交叉操作中產生的抗體群中隨機選擇變異位進行變異操作產生新的個體[12-13]。

3 算例分析

3.1 問題描述

本文以武漢某生鮮配送公司為例，對冷鏈物流配送路徑進行研究。該公司共有3輛車，對9個市內生鮮批發市場進行生鮮配送供應。每輛車額定載量均為w=4t,各參數數值如表1所示。配送中心與各批發市場之間、各批發市場之間的距離(km)及各批發市場貨物需求量(t)如表2所示，0代表配送中心，市場時間窗如表3所示。

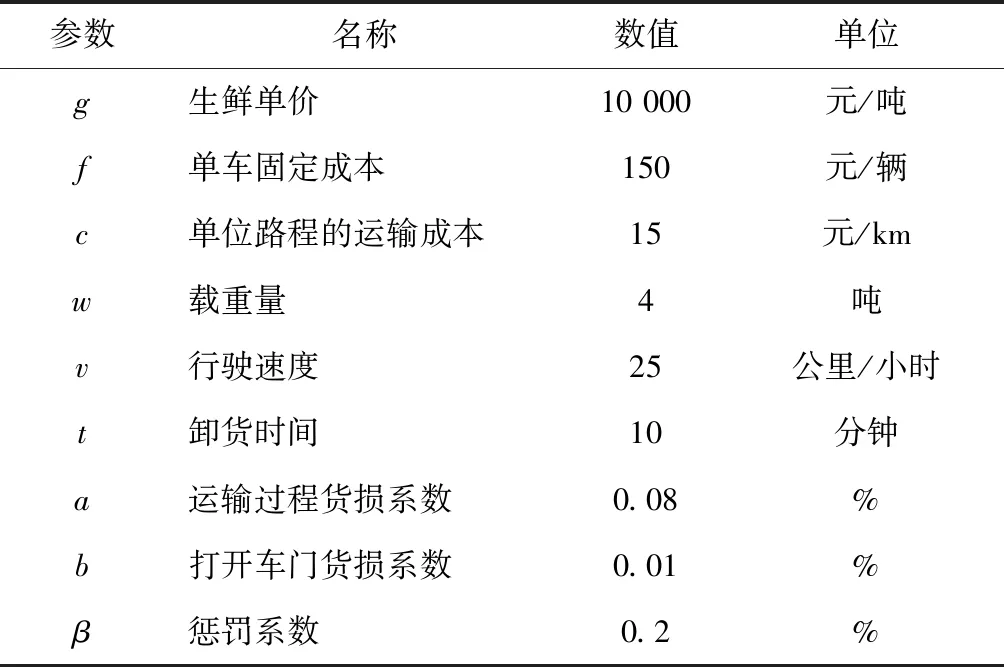
表1 各參數數值

3.2 優化免疫算法求解冷鏈物流最短配送路徑

通過理論分析及數學建模，基于免疫優化算法求解冷鏈物流配送路徑最優問題，可以通過編程實現，并通過對結果的分析，驗證了算法的有效性。

初始代生成是隨機的，給定群N=40，最大進化代數G=200 ，碼長L=27 ，交叉概率Pc=0.7，突變概率Pm=0.1。根據時間窗要求，預先設定客戶9為第一條線路的第一個客戶。通過編程，輸入約束條件，隨機求解6次，結果，如表4所示。

從計算結果可以看出，計算到61代時，首次搜到最優解，配送最低成本為2015.58元,且適應度最高。配送路徑各個車次都按照相應時間窗要求，將貨物送到，懲罰成本為0。當前每輛車都達到85%以上的滿載，但每輛車服務的客戶較少，同時生鮮配送公司離各批發市場較遠，這樣就造成了在這段路程上成本的浪費。另外一方面，每個批發商之間的距離是比較近的，從批發商到批發商之間耗費時間是比較少的，我們可以通過合理安排時間窗，把運輸車改為額定載量為5.5 t和6 t的貨車，這樣兩輛車就能完成所有貨物的配送，可以有效降低成本，減少資源浪費。

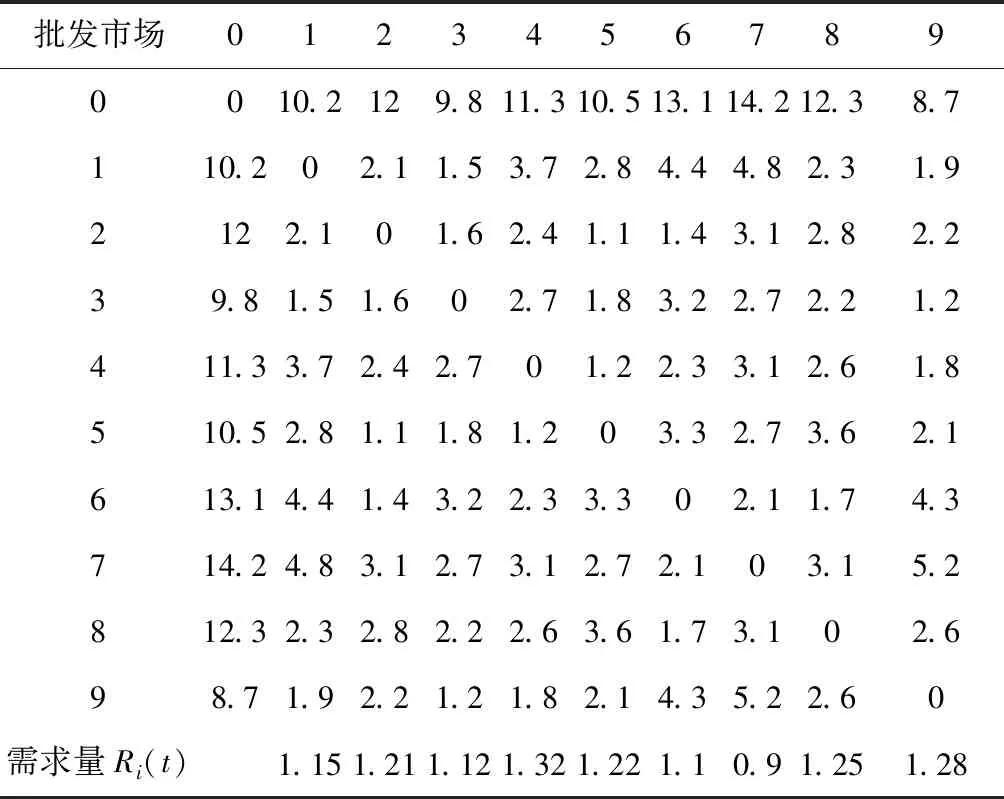
表2 配送中心與各批發市場之間、各批發市場之間的 距離及各批發市場貨物需求量

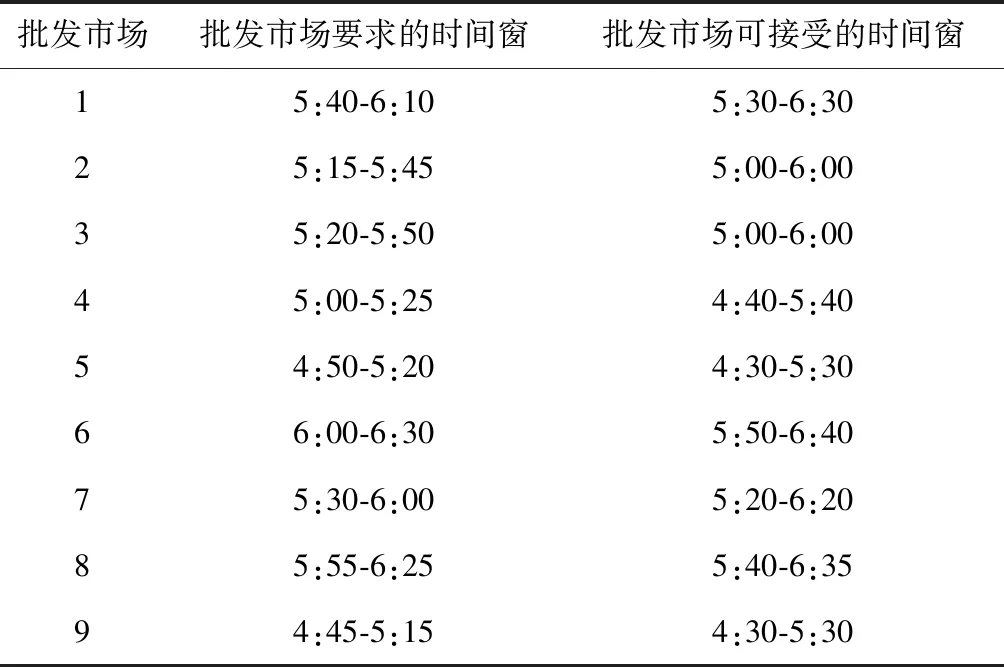
表3 各批發市場時間窗

表4 冷鏈物流配送路徑優化問題的免疫優化算法求解結果

為:0→9→3→1→0; 0→5→2→6→0; 0→4→7→8→0;如表5所示。

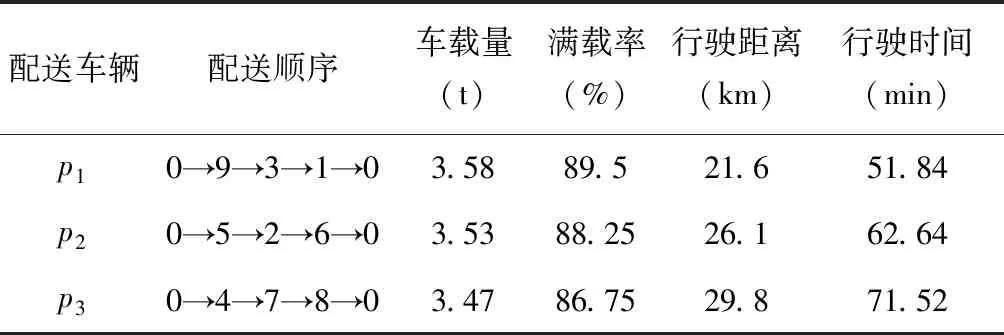
表5 配載情況表

由此可得，免疫優化算法可以方便有效地求得冷鏈物流配送路徑的最優解，為實際應用進行指導。

4 總結

本文研究了冷鏈物流配送路徑優化問題。基于免疫優化算法，通過數學模型的建立，加入時間窗及車輛載荷等約束條件，快速求得最優配送路徑。通過對實列的分析，可證明免疫優化算法對冷鏈物流配送路徑問題求解是合理有效的，免疫優化算法具有更高的收斂速度，沒有半早熟收斂，并且它可以在短時間內搜索最佳路徑。通過抑制高濃度的抗體并添加新的高適應度個體，免疫優化算法可以維持抗體的多樣性。同時，免疫優化算法通過選擇交叉和變異操作來保持良好的本地搜索能力，是一種有效的路徑優化方法。最后在具體實例中提出了更為合理的路徑安排方法，使得在配送過程中可以最大程度地節約成本，提升配送效率，保證生鮮產品的質量。