王亞林， 楊擁軍， 任 臣

(中國電子科技集團公司第十三研究所，河北 石家莊 050051)

0 引 言

微機電系統(micro-electro-mechanical system,MEMS)陀螺儀是一種基于哥氏力效應的角速度傳感器，具有低功耗、小體積、低成本、易集成等優點，廣泛應用于航空航天，汽車電子，機器人等領域[1,2]。傳統的MEMS陀螺儀測控系統主要由模擬電路構成[3]，由于模擬器件環境適應性、噪聲性能較差，使得陀螺儀精度難以進一步提升。相比模擬測控電路，數字閉環測控系統具有集成度高、可靠性好、不易受環境溫度影響、可實現各種復雜算法等優點，已成為MEMS領域的研究熱點[4]。數字閉環測控系統包括驅動環路和檢測環路，兩環路中都需要解調相關信號以獲取信號的幅值和相位信息，得到關鍵控制信號以便完成進一步控制和信號輸出[5]。因此，解調算法的優劣直接影響陀螺的性能。

本文提出了一種同步積分解調算法，相比傳統乘法解調[6]，該解調方式抗噪聲能力強，響應較快，硬件資源使用少。基于同步積分解調，設計了鎖相環+自動增益控制(phase-locked loop+automatic gain control,PLL+AGC)雙閉環驅動系統，實現了陀螺驅動模態諧振。

1 MEMS陀螺工作原理及測控系統設計

1.1 陀螺工作原理

MEMS陀螺原理圖如圖1所示。

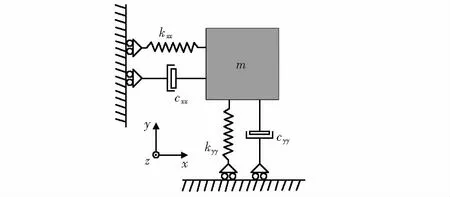
圖1 MEMS陀螺原理

MEMS陀螺具有驅動和檢測兩個模態，兩種模態均可看作二階質量—彈簧—阻尼系統[7]，其動力學方程為

(1)

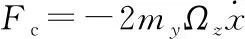
(2)

陀螺工作時，保證驅動模態處于諧振狀態，即ωd=ω，驅動、檢測位移分別為

(3)

(4)

1.2 陀螺測控系統

本文檢測模態采用開環方式。陀螺整體測控系統如圖2所示。系統為一個數/模混合電路，模擬部分主要有電容電壓(C/V)轉換電路、放大電路、模/數轉換器(ADC)等，數字部分主要有PI控制、(AGC)等。采用AGC+PLL方案，陀螺在驅動方向處于諧振狀態。角速度引起檢測位移y導致梳齒電容變化，信號經過C/V，放大電路，解調輸出角速度信號。

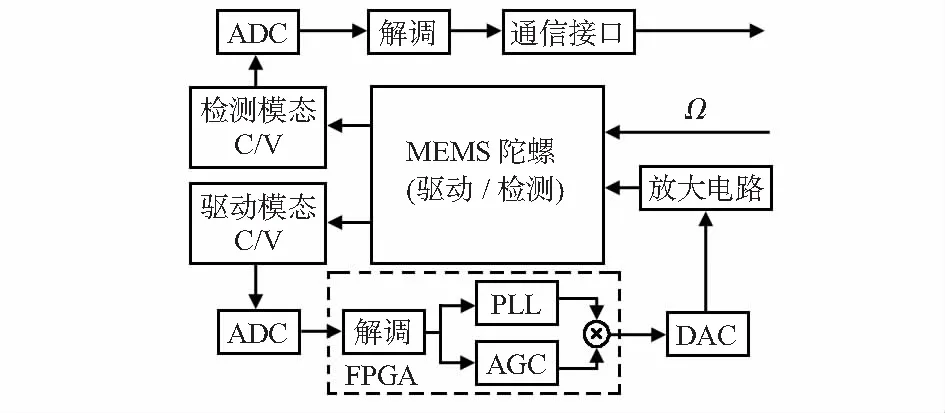
圖2 MEMS陀螺測控系統圖

2 同步積分解調算法設計

由1.2陀螺測控系統系統原理可知，幅度和相位信息作為環路中的重要控制信號對系統功能實現至關重要，陀螺的驅動環路、檢測環路都需要解調環路中的信號從而得到對應信號的幅度和相位信息。MEMS陀螺信號傳統的解調方式是乘法解調，該解調算法抗噪性能較差，且解調信號伴隨二倍頻成分，其引入的低通濾波器導致系統相位延時。本文設計了一種新的解調算法即同步積分解調，實現陀螺驅動模態、檢測模態的信號解調。

2.1 同步積分解調原理

同步積分器電路原理圖如圖3所示[8]。

圖3 同步積分器電路

同步開關控制電阻R與C1、C2連接(開關高電平時R與C1連接，低電平時R與C2連接)，設C1=C2，輸入信號為

Vi(t)=A1sin((ωc+Δω)t+φ)

(5)

式中ωc為同步開關信號頻率，Δω為輸入信號與同步信號的頻差

(6)

θ=arctg(2R1C1Δω)

(7)

(8)

為了較容易地獲得輸入信號的幅值和相位，只需要對當前通道1的同步積分電路添加另一路與之正交的通道2。通道2的輸出電壓可以表示為

(9)

因此，輸入信號的幅值和相位表達式可以最終表示為

(10)

同步積分解調的實際結構如圖4。

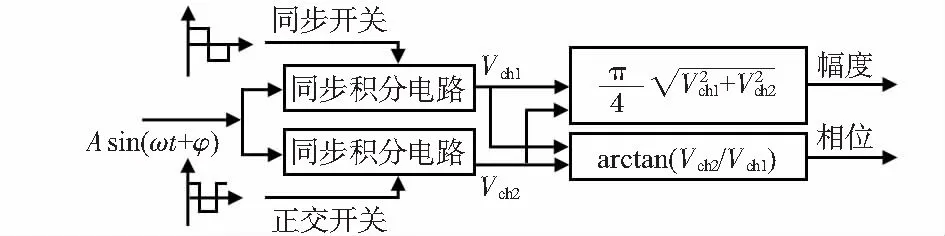
圖4 同步積分解調結構

2.2 同步積分解調仿真

2.1中的分析基于一階同步積分器，事實上同步積分器可以級聯成多階，多階同步積分器具有更好的噪聲抑制能力。本文采用三階同步積分器。其傳遞函數為

(11)

解調帶寬為Bw=0.194 28/(2RC)，本文設計帶寬為100 Hz。R=8 kΩ，C=15 nF。

分別設計了同步積分解調和傳統的乘法解調并在相同的條件下仿真。乘法解調結構如圖5所示[9]。

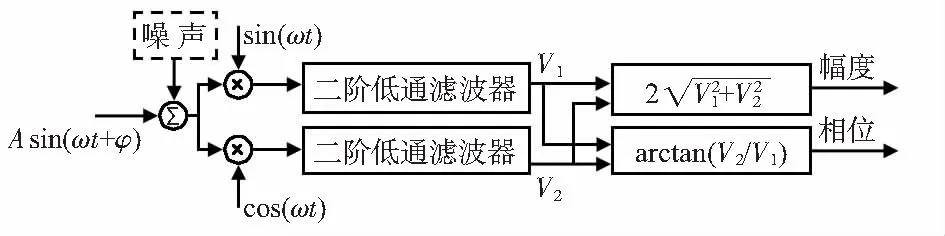
圖5 乘法解調原理

輸入信號為幅度1 V，頻率4 096 Hz，初始相位30°的正弦波信號，經過同步積分解調和乘法解調輸出信號的幅值如圖6所示。圖6表明，同步積分解調啟動時間為8.4 ms，乘法解調啟動時間為13.8 ms。

圖6 解調輸出

在以上正弦信號中疊加一個均值0 V，標準差0.05 V的高斯白噪聲，對兩種解調得到的信號進行頻譜分析，得到頻譜如圖7所示。結果表明同步積分解調的信號幅值只有直流成分，而乘法解調存在明顯的二倍頻成分(如圖虛線部分)，這對解調速度和精度有一定影響。兩種解調算法的抗噪聲能力分別為-190，-140 dB。同步積分解調具有更好的抗噪聲性能。

圖7 信號+噪聲解調輸出頻譜

3 閉環驅動系統設計

諧振式陀螺要實現角速度的精確測量，應保證陀螺質量塊驅動幅值和頻率的穩定性[10]。因此驅動模態采用閉環方式，本文設計了雙閉環控制網絡實現MEMS陀螺驅動振幅和頻率的穩定控制。其中自動增益控制(AGC)閉環實現MEMS陀螺恒幅振動，數字鎖相環(PLL)實現驅動頻率及相位跟蹤與控制。

3.1 自動增益控制[11]

陀螺驅動閉環AGC原理如圖8所示。

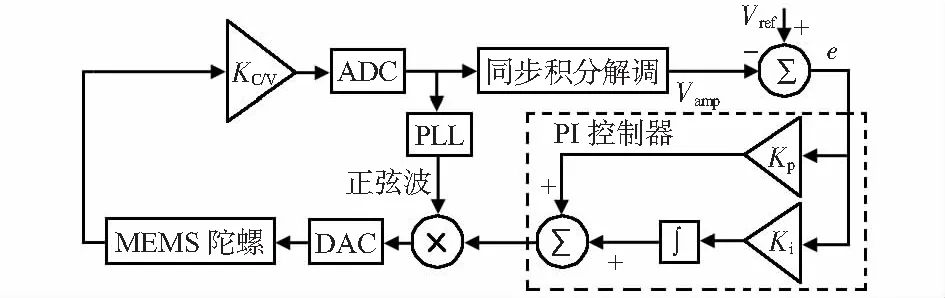
圖8 AGC系統結構

經典PI控制器，其傳遞函數為

(12)

當陀螺振動引起的電壓變化幅值大于參考值Vref時，殘差信號變成負值，PI控制器輸出減小即驅動信號減小，陀螺振動角度位移減小;反之陀螺振動位移增加。通過AGC控制最終陀螺的振動位移將穩定在參考值Vref附近。

3.2 鎖相控制

PLL是一個相位誤差閉環控制網絡，在MEMS陀螺驅動閉環控制系統中，鎖相環控制陀螺驅動信號與驅動檢測信號保持90°相位差，保證陀螺始終工作在諧振狀態。PLL閉環控制如圖9所示。

其中數字振蕩器NCO根據輸入信號產生兩路頻率可調、幅度穩定、相位正交的數字正弦信號。NCO傳統的實現方法主要有查表法、多項式展開法、近似法等，但這些方法在速度、精度、資源方面難以兼顧。采用CORDIC算法，無需使用乘法器，利用簡單的移位和相加運算，即可產生高精度的正余弦波形，尤其適合于FPGA的實現[12]。本文研究采用16級流水線結構的CORDIC算法實現數控振蕩器。該數控振蕩器的原理如圖10所示[13]。

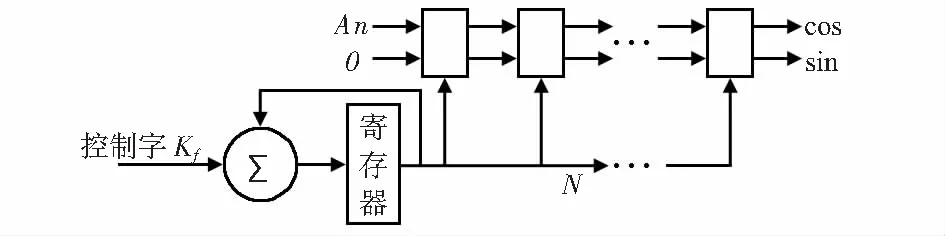
圖10 NCO結構

時鐘信號控制相位寄存器每次以累加，然后以其對應的角度值作為輸入進行N次迭代運算。每一級迭代運算中加入寄存器，就得到并行流水線結構的CORDIC算法。CORDIC算法的迭代次數決定了相位精度，精度表示為θ=arctan(2-N)180/π。

輸出信號的分辨率取決于相位累加器的位寬B，分辨率可表示為f=fs/2B。其中，B為相位累加器的位寬，fs為系統時鐘頻率。設輸入頻率控制字的字長為m，DCO的中心頻率為，則該DCO輸出頻率范圍為[fmin,fmax]fmin=f0+2m·fs/2B,fmax=f0-2m·fs/2B。該振蕩器幅度量化誤差為ΔV=2-(n-1)=2-15=3.052×10-5V。頻率量化誤差為Δf=fs/2B=100×106/232=0.023 Hz。在SIMULINK中建立完整的驅動閉環系統，仿真結果如圖11所示。結果表明同步積

分解調可以用于MEMS陀螺中，陀螺起振時間為0.12 s，驅動位移為4.738×10-6m。

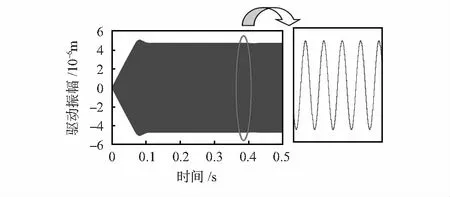
圖11 驅動閉環仿真結果

4 結 論

本文設計了一種新的解調算法即同步積分解調，通過仿真該算法比傳統乘法解調具有更好的噪聲性能、更快的啟動時間，基于該解調算法設計了MEMS陀螺雙閉環驅動系統，采用AGC和PLL技術保證陀螺恒幅恒頻振動。仿真結果表明陀螺成功起振。