基于模糊隨機PWM技術的永磁直線電機性能分析*

汪旭東, 史凱寧, 許孝卓, 孫偉翔

(河南理工大學 電氣工程與自動化學院,河南 焦作 454000)

0 引 言

變頻變速永磁直線電機(permanent magnet linear motor,PMLSM)因其高效率和出色的速度調節被廣泛應用于工業生產和生活中[1,2],然而變頻器電源在開關頻率整數倍附近會產生較大高次諧波,這些諧波會造成電磁激振力頻率與電機的一些模態固有頻率產生共振,使電機產生振動噪聲[3～6]。因此,降低變頻器輸出電壓頻譜中的高次諧波可以增加電機的穩定運行性。

目前,隨機脈寬調制(pulse width modulation,PWM)技術[7]是較常用的開關頻率切換方法,它將一定概率分布的隨機信號添加到開關信號上,使得最初集中在開關頻率上的幅值分布在整個頻域范圍內,從而有效抑制開關電源驅動電路中存在的傳導電磁干擾(electromagnetic interference,EMI)。文獻[8]中的隨機載波頻率方法是通過隨機改變切換周期的長度來改變切換頻率,這使一定頻率范圍內的輸出頻譜分布更加均勻。但是當在一個或多個周期中改變切換周期時,采樣周期和切換周期需要同時動作,則采樣周期也必須以相同的方式改變,這在實際中難以實現。文獻[9]采用固定載波頻率,將開關頻率保持在恒定值,并在每個開關間隔中隨機改變脈沖位置,使得切換位置始終在間隔內,操作更加簡便。

本文提出了一種新的開關模式,即模糊隨機脈沖位置調制(FRPPM),在自適應模糊控制器下,通過在恒定開關頻率下隨機改變脈沖位置使電壓頻譜中產生均勻的諧波分布。在MATLAB / SIMULINK軟件中搭建永磁直線電機控制模型,仿真結果表明FRPPM方法使輸出電壓的頻譜分布更加均勻,降低了開關頻率附近的高次諧波,同時也改善了氣隙磁場的諧波,有效地抑制了EMI問題。

1 變頻器供電下永磁直線電機氣隙磁場分析

永磁直線電機氣隙磁密的表達式為

b(x,t)=f(x,t)λ(x,t)

(1)

式中f(x,t)為氣隙磁動勢,λ(x,t)為氣隙比磁導。

在正弦電源供電時,PMLM的氣隙磁動勢可分為基波磁動勢、繞組諧波磁動勢和永磁體等效磁動勢,即

f(x,t)=fm0(x,t)+∑fmν(x,t)+∑fμ(x,t)

(2)

比較永磁直線電機的變頻驅動與正弦電源,繞組諧波磁動勢將分為由基波電流作用下的諧波磁動勢和δ次變頻器供電電流產生的諧波磁動勢[10]。其中后者可能導致永磁直線電機產生振動和噪聲。PMLSM的4種磁動勢[11]表示為：

PMLSM的基波磁動勢

(3)

永磁體等效磁動勢

(4)

繞組ν次諧波磁動勢

(5)

δ次變頻器供電電流產生的諧波磁動勢

(6)

定子開槽氣隙比磁導

(7)

式中τ為極距,τs為齒距,ω0=2πf0,f0為電源基波頻率,λ0為不變部分,λn為諧波相對磁導函數的周期分量將式(2)～式(6)代入式(1)中,可得永磁直線電機氣隙磁場表達式為

(8)

2 FRPPM方法

2.1 模糊控制器的設計

2.1.1 輸入量的選擇

由于傳統比例—積分(proportional-integral,PI)控制器無法對突然變化的誤差信號e作出反應,只能確定誤差信號的瞬時值,因此采用對誤差信號求導并引出分支ec的方法,并以差量e和差量變化ec作為模糊控制器的參數信號,通過對輸入量進行模糊化、構建隸屬度及模糊規則、論域整定等步驟設置合適的模糊控制器參數,并以K′p,K′i為模糊控制量的輸出,作為整定參數傳遞給PI控制器調節參數以進行選擇合適的Kp,Ki參數。其中,模糊邏輯控制結構如圖1。

圖1 模糊規則控制結構

2.1.2 模糊語言與隸屬度函數的設計

輸入量的模糊化是用模糊語言代替自然語言[12],采用模糊控制技術將具有突變性的誤差信號進行模糊化,并通過采用人腦的邏輯推理能力進行參數的確定。設定模糊規則的子集為{NB,NM,NS,Z,PS,PM,PB},且e,ec和K′p,K′i的具有相同的模糊子集,這些輸入輸出變量分別對應的模糊名稱為負大(NB),負中(NM),負小(NS),零(Z),正小(PS),正中(PM),正大(PB)。其中模糊推理采用Mamdani方法[13]。

2.1.3 模糊規則的建立

依據經驗和仿真實驗得到K′p,K′i的模糊規則如表1。

表1 模糊控制規則表

PI參數主要包含兩個變量的整定,針對模糊控制規則參數選定原則如下:1)變量e較大,不考慮ec,取較大的Kp和較小Ki,以加快系統響應；2)變量e適中,取較小的Kp和Ki,以在響應速度一定的情況下,使系統超調較小；3)變量e較小或為零,取較大的Kp和Ki,以防止系統振蕩。

2.2 隨機脈沖位置方法

傳統隨機脈沖位置調制方法是使用兩個頻率相同,具有整數倍關系的波,通過正負調制和改變斜率來實現隨機脈沖位置的改變。其中,這兩個相同頻率的波的斜率也相等,脈沖位于切換間隔的中心。當斜率的大小改變,合成載波波形的周期保持不變時,脈沖的位置則會在切換間隔中發生移動,脈沖位置變化如圖2(a)所示。當斜率以隨機方式改變時,脈沖位置會在切換間隔里面發生隨機變化,且不發生越界現象。在該方法中,當斜率趨于無窮大時(即為垂直線),就可以得出脈沖位于切換間隔的開始或結束位置,如圖2(b)所示。

圖2 不同頻率下的脈沖位置及切換間隔內最大脈沖位移

當斜率以隨機方式改變時,為計算波形的上升斜率和下降斜率,此時采用線性同余方法進行生成隨機數[14,15]。

線性同余法遞推公式為

xi+1=mod(axi+c,m),Ri+1=xi+1/m

(9)

式中i=0,1,2,3…；x0為隨機數的起始值；mod為取余運算符；a為乘數；c為變量；m為模量。當a和m的值選取合適時,可將每個xi縮放到單位間隔(0,1)中。

對于波形上升頻率和下降頻率的時間為

Tu=Rn×T,Td=(1-Rn)×T

(10)

式中Rn為隨機數,Tu為上升斜率時間,Td為下降斜率時間,T為載波轉換時間。

如圖3(a)所示,為不同隨機數值的載波波形和PWM脈沖。其中脈沖寬度在切換間隔沒有改變,通過改變隨機數來改變其位置。

表2為隨機序列在兩個載波頻率之間以及正、負載波模式間進行選擇,并通過兩個隨機位:A和B,以顯示如何通過不同的A和B值選擇開關頻率和正負模式(A用于正模式和負模式的選擇,B用于選擇載波頻率)。

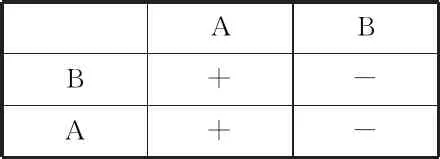
表2 載波頻率和正負調制的選擇

圖3(b)為所提出的隨機切換技術的最終波形。將這些波形與模糊規則制定的矢量控制波形進行比較,以產生PWM逆變器的控制脈沖。

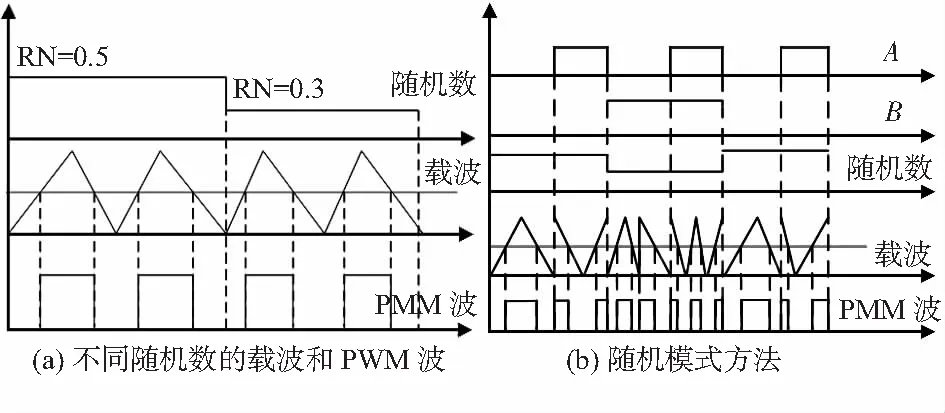
圖3 不同隨機數的載波和PWM波與隨機切換最終模型

3 仿真研究

本文利用MATLAB/SIMULINK 和Magnet搭建矢量控制電路的聯合仿真模型,如圖4所示。

圖4 基于模糊控制的感應電機原理圖算法

分別對隨機PWM 調制方式和FRPPM方式進行仿真分析。其中,逆變器相關參數為：U=545 V,L=350 μH,R=10 Ω,開關頻率f=10 kHz,系統的仿真時間設為0.5 s。電機模型采用16極15槽的雙邊永磁直線電機,其運行頻率f=23 Hz,動子運行速度v=1.035 m/s,極距τ=22.5 mm。仿真結果如圖5所示,其中,圖5(a)和圖5(b)分別為兩種不同控制模式下逆變器供電電壓的頻譜；圖5(c)和圖5(d)分別為不同控制模式下電機氣隙磁場波形。

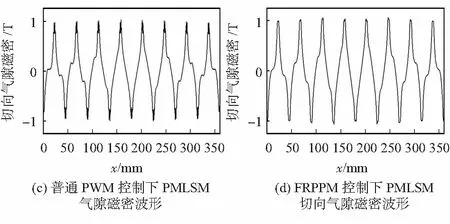
圖5 仿真結果

根據仿真結果顯示,采用傳統隨機PWM控制下的電壓存在高次諧波,峰值最大為15 V,且電機橫向切向氣隙磁密的峰值也存在諧波；而利用RFPPM方法,電壓諧波成分明顯減小,電壓幅值得到降低,峰值最大值為2 V,比隨機 PWM減小了86 %,電機中的橫向切向氣隙磁密諧波也相應減少。通過仿真結果對比分析可以看出,采用RFPPM方法可以有效削弱電壓頻譜的集中高次諧波簇,使得在較寬的頻帶范圍內輸出電壓諧波成分分布更加均勻,也降低了永磁直線電機氣隙磁場的諧波。

4 結 論

本文在隨機PWM基礎上提出了一種新的FRPPM方法,與隨機PWM控制策略分別在MATLAB/SIMULINK搭建永磁直線電機矢量控制電路,仿真結果對比表明采用FRPPM方法可以明顯降低開關頻率附近的集中高次諧波簇,使電壓頻譜在較寬的頻率范圍內分布的更加均勻,同時在不增加濾波設備的情況下,能夠有效的改善電機氣隙磁場波形,結果驗證了所提方法的有效性及可行性,為進一步對直線電機控制的實際應用奠定了理論基礎。