基于SAW微力傳感器的GRNN擬合研究*

季雪咪, 李媛媛, 李濟同

(上海工程技術大學 電子電氣工程學院,上海 201620)

0 引 言

聲表面波(surface acoustic wave,SAW)技術在聲學領域、電學領域和半導體學領域發展迅速[1],所制傳感器能夠敏感多種物理量[2],且憑借微型化、可集成度高、無源無線等優勢被廣泛應用[3],如SAW微力傳感器。然而在測量過程中,傳感器受外界環境中溫度、濕度、空氣等流體影響,易產生測量誤差使輸出數據點是離散的,難以直觀體現傳感器特性。以實測的離散數據點為依據預測數據值,將離散數據擬合為連續曲線[4],為后續分析傳感器線性度、穩定性和準確度打下基礎。因此,提高傳感器輸出特性曲線精確度一直是研究人員所關注的問題。

擬合傳感器輸入—輸出特性曲線的方法通常有分段線性化法[5]、最小二乘法[6]和反向傳播(back propagation,BP)神經網絡[7]等。然而,分段線性化法需要分段,計算過程隨著分段段數的增加而越復雜,且精確度不高;最小二乘法無法全局搜索,易求得局部最優解,且會出現病態矩陣方程失去有效性[8];BP神經網絡模型構建繁瑣,在學習過程中收斂速度慢,訓練過程中又會陷入誤差性能函數局部最小情況[9]。

針對上述傳統方法的不足,本文結合SAW微力傳感器,根據廣義回歸神經網絡(general regression neural networks,GRNN)和最小二乘法基本理論,借助 MATLAB R2016b編程環境,分別對測得的數據進行曲線擬合,并分析比對擬合結果。

1 SAW微力傳感器

1.1 SAW微力傳感器原理

本文選取SAW微壓力傳感器為延遲線型結構,如圖1所示。該傳感器兩端固定,壓電基片上的兩側分別沉積輸入和輸出叉指換能器,外界壓力施加于基片中間。基片材料具有非線性彈性行為,當外界壓力F施加在壓電基片上時,材料的彈性常數、密度等會因壓力大小的不同而發生變化,導致SAW傳播速度隨之改變。與此同時,基片中間受力導致SAW傳感器的結構尺寸發生改變,引起SAW波長的變化。波速和波長變化導致諧振頻率的變化,通過頻率與壓力間關系獲取傳感器特性[10]。

圖1 延遲線型原理

1.2 SAW微力傳感器選取

壓電基片材料通常使用石英、鈮酸鋰、鉭酸鋰、氧化鋅等。理想情況下要求壓電材料具備高機電耦合系數、低溫度系數、高壓電系數等[11]。綜合對比可得鈮酸鋰的壓電性能優于其他材料,因此,本文采取由鈮酸鋰制成的SAW微力傳感器,長度L1=21 mm,寬度L2=5 mm,厚度H=1 mm,如圖2所示。

圖2 SAW微力傳感器

1.3 數據采集

本文選取E5061A型網絡分析儀對鈮酸鋰所制SAW微力傳感器進行輸出頻率測量。將傳感器兩端引腳固定于測量銅座,銅座的兩個端口通過傳輸線與網絡分析儀連接。0～20 g的砝碼表示外界微力,采用細線一端纏繞在傳感器基片中間,另一端懸掛砝碼,從而達到施加微力的效果。以0 g為起點,逐克遞增至20 g,每增加1 g記錄一次頻率數據,傳感器數據采集如圖3所示。

圖3 數據采集

在測量過程中,由于頻率波動較大,需要穩定一段時間后讀取數據,每克微壓下記錄10次頻率數據,求得平均后選取20組數據,在后期數據處理時可獲得對傳感器輸出特性更加精準的分析。SAW微力傳感器輸入壓力和輸出頻率數據見表1。

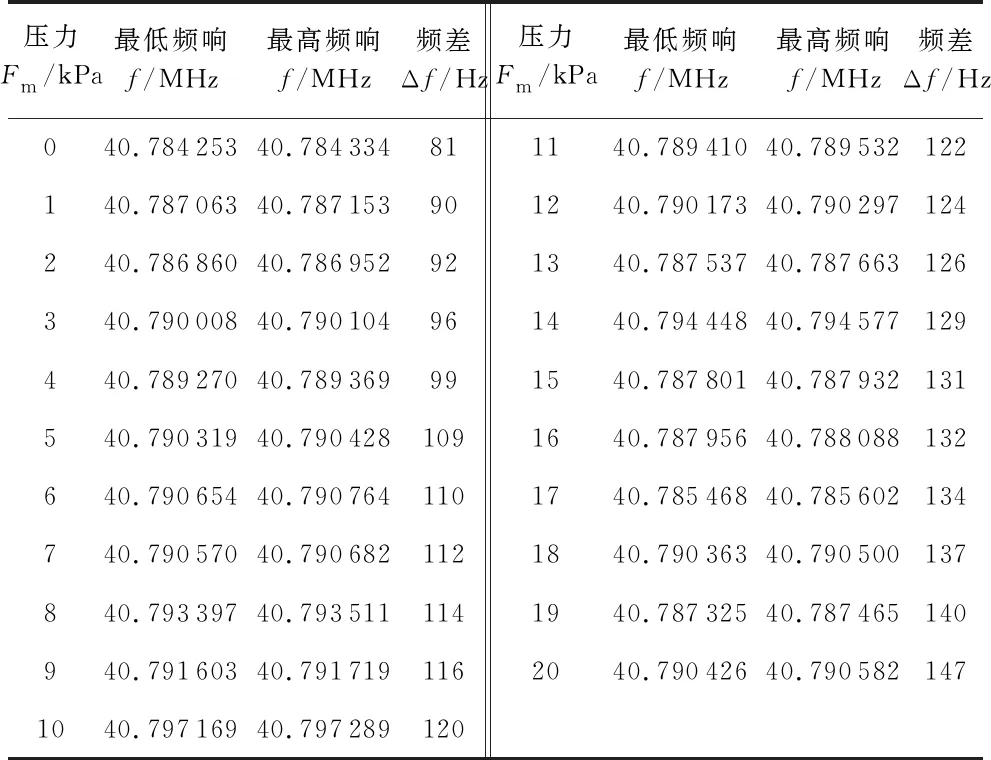
表1 壓力與頻率數據表

2 GRNN曲線擬合

2.1 GRNN基本理論

GRNN與徑向基神經網絡相似,是以概率密度函數為基礎的核回歸方法,具有模型結構簡單、人為調整參數少、收斂速度快等優勢[13]。

GRNN主要目的是計算能夠輸出最大概率值的y。假設自變量x和因變量y,兩者的聯合概率密度函數用f(x,y)表示,則y的預測輸出[14]為

(1)

已知訓練樣本數據集為{xi,yi}ni=1,應用Parzen-Rosenblatt非參數估計,密度函數f(x,y)按式(2)估算獲得

(2)

式中n為訓練樣本容量,p為自變量x的維數,s為擴展系數,亦稱為光滑因子。將式(2)代式(1)可得

(3)

2.2 GRNN仿真建立

GRNN神經網絡的模型構建不復雜,需要人為調節參數少,其中包括閾值b

(4)

式中 參數s(即為擴展系數)為徑向基神經網絡的分布密度,從式(2)、式(3)中可以發現,當擴展系數非常大時,對實測擬合的曲線越光滑,但伴隨的誤差也非常大;當擴展系數非常小時,擬合曲線越逼近于實測數據,擬合精度更高,但易出現過擬合現象[15]。因此,擴展系數對GRNN的擬合精度和曲線光滑程度有著重要的影響。通過反復驗證,擴展系數選取1.0。

SAW微力傳感器包含2個變量,分別是最高頻率與最低頻率間差值Δf和所受微壓力Fm。在MATLAB R2016b環境下編程,使用(f,F)表示頻率和壓力的函數關系。newgrnn函數是設計GRNN神經網絡的核心函數

net=newgrnn(f,F,s)

在廣義回歸神經網絡算法下的頻率與壓力曲線擬合效果圖如圖4所示。

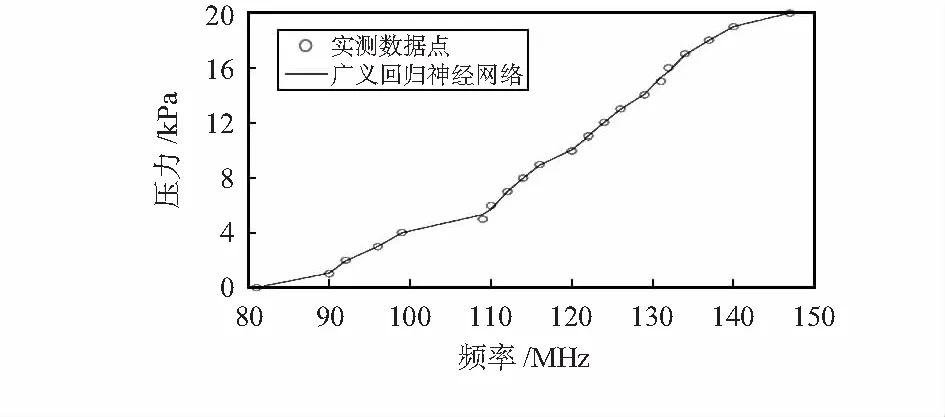
圖4 GRNN擬合效果

3 最小二乘法曲線擬合

3.1 最小二乘法基本理論

最小二乘法是一種搜索優化方法,主要目的是將擬合數據與實際測量數據間誤差平方和達到最小[16]。假設給定樣本數據為{(xi,yi),i=1,2,…,m},且需擬合的曲線函數為f(x,α),其中，α=(a0,a1,…,an)表示權系數。令

(5)

欲使誤差平方和達到最小,對其求偏導并等于0,則

j=0,1,…,n

(6)

化解可得

(7)

α=(a0,a1,…,an)所求就是擬合曲線函數的解,此時殘差平方和最小,擬合效果最佳。

3.2 最小二乘法仿真建立

給定SAW微力傳感器輸入壓力,測得輸出頻率數據,則分別設為Fi和fi,i=1,2,…,n,令n=6,擬合函數為

(8)

在MATLAB R2016b環境下編程,調用Ployfit函數。

p=ployfit(f,F,6)

編程獲得在最小二乘法算法下的頻率與壓力曲線擬合效果圖如圖5所示。

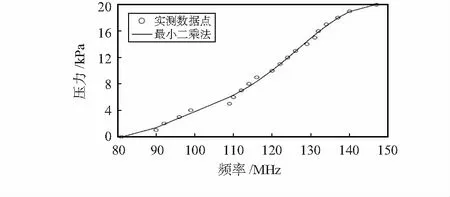
圖5 最小二乘法擬合效果

4 GRNN和最小二乘法擬合對比

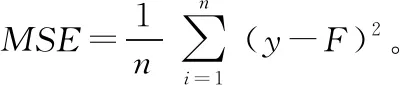
表2 三種誤差統計表

由表2可以看出,GRNN的三項誤差值都小于最小二乘法,最大絕對誤差為-0.335 5,而最小二乘法最大絕對誤差高達0.646 8。GRNN最大相對誤差不超過-0.067 1,在相對應的數據點處,最小二乘法相對誤差為-0.201 9。同時,GRNN的均方誤差為0.017 8,最小二乘法為0.118 5,GRNN的均方誤差小于最小二乘法,達1個數量級。為更直觀地顯示GRNN和最小二乘法的精度高低,采用折線圖描述絕對誤差和相對誤差數據,并放入同一張圖進行對比,如圖6所示。

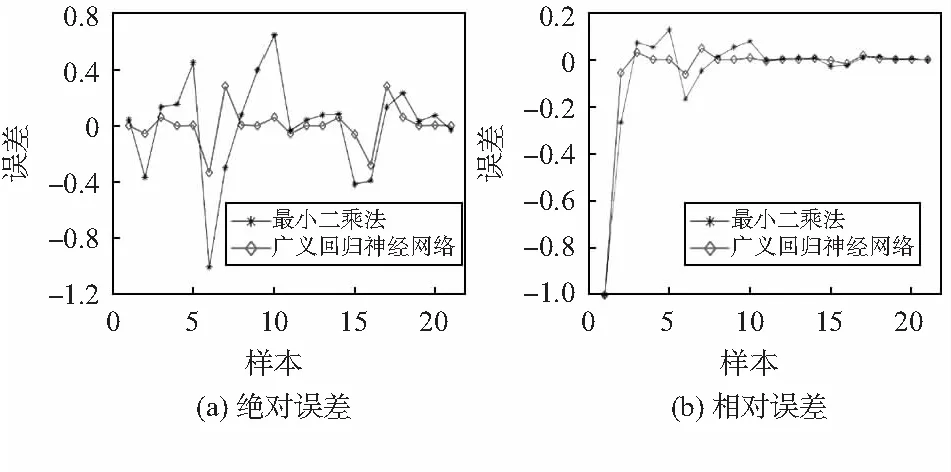
圖6 兩種算法的絕對誤差和相對誤差

由絕對誤差對比圖可以看出,GRNN在-0.3～0.3范圍內波動,波動幅度較大的僅有4個數據點,其余數據點均逼近零。然而最小二乘法誤差曲線上下波動范圍大,最大高達-0.368 0。一般認為相對誤差小于等于5 %滿足精度要求,由相對誤差對比圖可以看出,GRNN相對誤差在5 %范圍內浮動,最小二乘法波動大,達10 %以上。由此可見,采用GRNN對器件承載的外界微力進行預測和擬合,曲線的整體誤差和精確度準確度,均優于最小二乘法。

5 結 論

本文以SAW微力傳感器為基礎對比分析GRNN和最小二乘法的曲線擬合效果。仿真結果表明：GRNN和最小二乘法都能夠在實測數據相同的情況下實現曲線擬合,而GRNN的相對誤差和絕對誤差明顯小于最小二乘法,均方誤差更是少1個數量級,擬合精度更高。其次,GRNN對于一些不穩定數據,擬合效果更佳,且模型構建簡單,需自行調整參數少。由此可見,利用GRNN提高SAW微力傳感器輸入壓力與輸出頻率擬合曲線精度的方式有效且可靠。