行星齒輪箱齒輪磨損故障診斷
李海平,趙建民,張 鑫,倪祥龍
(1.軍事科學院 系統工程研究院,北京 100141;2.陸軍工程大學 裝備指揮與管理系,石家莊 050003;3.中國洛陽電子裝備試驗中心,洛陽 471003)
行星齒輪箱與定軸齒輪箱相比,前者可以在相對狹小的空間內提供更大的傳動比因而被廣泛應用于如風機、直升機、起重機等大型復雜機械設備之中。然而,長時間低速重載的工作條件以及其結構上的特殊性也使相應的故障診斷工作具有自身的特點和難點[1-2]。
傳統的行星齒輪箱故障診斷方法從動力學建模的角度分析其正常運轉及各部件故障發生機理,然后分析各種故障對應的頻譜總結出規律來進行故障診斷[3-7]。這種故障診斷方法對專業性要求比較高,需要對行星齒輪箱的結構特點和故障對應的頻譜規律有比較透徹的理解。近年來研究比較多的是一些智能的故障診斷方法,通常包括信號采集、信號處理、特征提取和智能分類等。Paul等[8]介紹了基于振動的直升機傳動機構故障診斷有關研究綜述,包括常用的特征參數和故障診斷技術等。Liu等[9]提出一種核聚類分析方法來實現特征選擇和不同嚴重程度的行星齒輪箱齒輪磨損故障診斷。Feng等[10]利用集合經驗模態分解和能量分離方法實現風機行星齒輪箱的故障診斷。這些智能故障診斷方法通常需要進行信號處理和特征提取,需要一定的專業基礎,同時有些方法計算過程很復雜,不易于應用。
深度學習因可以直接將采集到的原始振動信號輸入到模型之中,而不需要進行特征提取和選擇這類要求具備專業知識的信號處理過程而被廣泛應用。深度置信網絡(Deep Belief Networks,DBN)作為第一個提出的深度學習訓練算法,不管在應用還是算法的改進都有廣泛的研究,是目前研究和應用都比較廣泛的深度學習結構[11]。He等[12]提出一種基于DBN的齒輪傳動系統故障診斷方法,取得了很高的故障診斷準確率。然而,在應用DBN時,原則上訓練集和測試集的每個樣本要包含設備運轉至少一個周期的數據,即確保每個樣本能包含足夠反映設備狀態信息的數據。在采集設備振動信號的過程中,如果采樣頻率比較低則可能導致一個周期數據不足以反映設備狀態,所以采樣頻率通常很高,這就導致每個樣本的數據點數比較大。而DBN要求的訓練樣本量又很大,訓練樣本多、輸入數據維度大,造成DBN的訓練時間非常長。因此,將DBN應用到機械系統故障診斷領域需要解決的首要難點問題就是在保證診斷準確率的前提下減少訓練時間。
減少智能診斷模型訓練時間最常用也是最有效的方法就是數據降維,將原本維度很高的樣本降至比較低的維度來減少計算量從而縮短訓練時間,特征提取可以算是數據降維的典型代表。主成分分析(Principal Component Analysis,PCA)方法由于易實現且概念簡單等優點被廣泛應用于數據降維。為了提高診斷精度,在應用PCA時通常要分析多個傳感器采集到的信號。如果只是簡單疊加多路信號的PCA分析結果直接作為診斷模型的輸入,就沒有考慮各路信號之間的聯系,也會影響診斷精度。歐氏距離技術(Euclidean Distance Technique,EDT)是使用較為廣泛的表示二者之間距離關系的算法,其同樣具有理論知識簡單且計算速度快的優點。
因此,本文利用PCA方法實現數據降維,然后采用EDT計算結果表示多個傳感器信號的PCA結果之間的關系,將兩種結果作為樣本輸入到DBN模型中得到診斷結果。該方法理論簡單易懂,算法易于實現,計算結果準確,而且大大減少了計算時間。
1 基于DBN的傳統方法分析
本節對基于DBN的傳統故障診斷方法進行研究,主要分析基于原始數據、FFT和特征參數三種情況下的DBN診斷性能。在分析過程中借助行星齒輪箱齒面磨損預置故障實驗數據來進行。
1.1 行星齒輪箱齒面磨損預置故障實驗
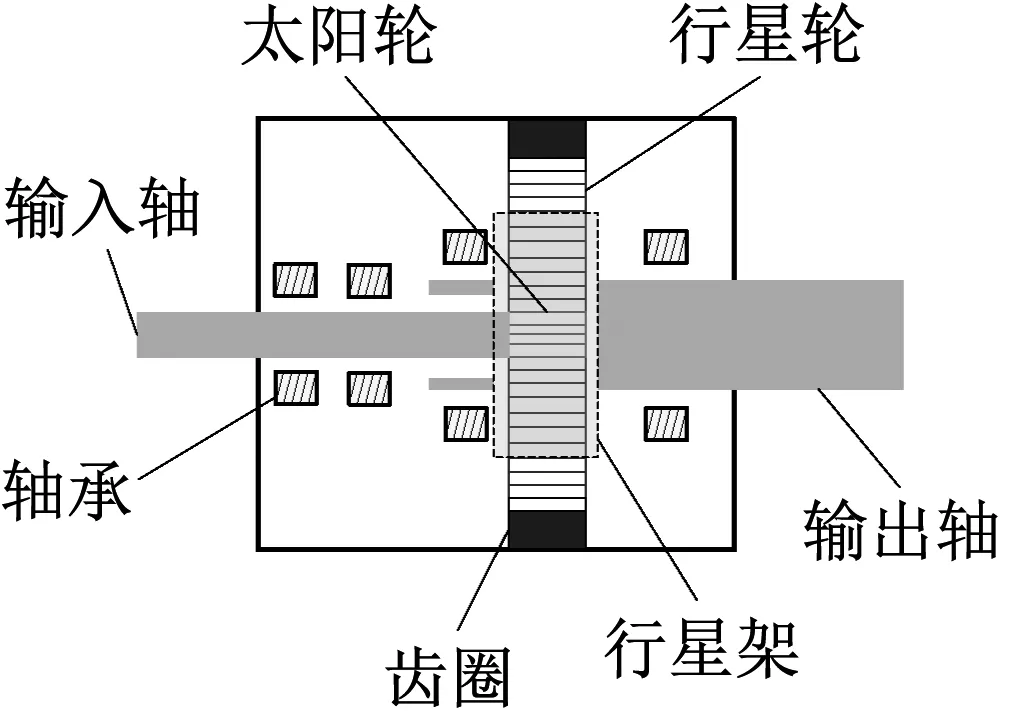
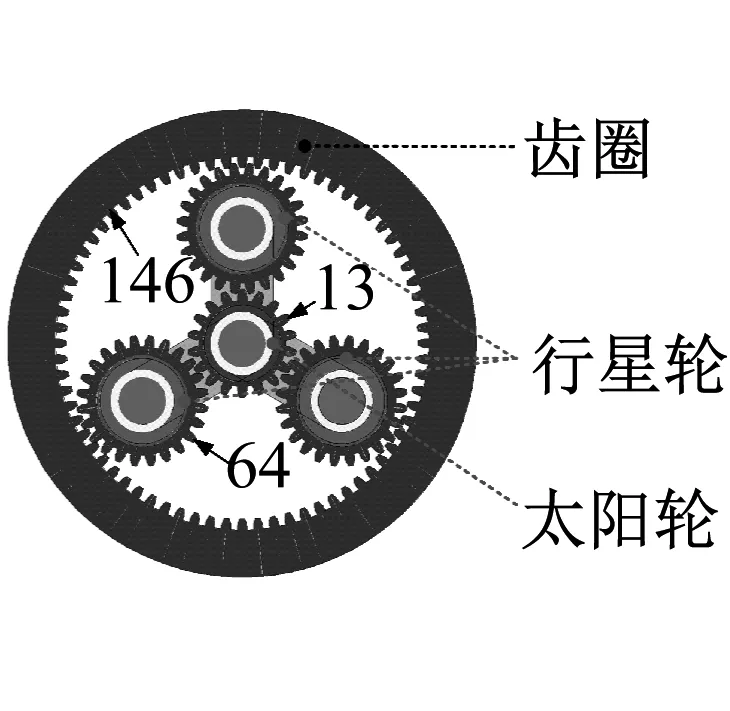
實驗系統如圖1所示,由實驗用行星齒輪箱、三相異步電磁調速電機、風冷磁粉制動器、轉速轉矩傳感器以及組成。該齒輪箱為單級行星齒輪箱,由1個太陽輪(齒數為13)、3個行星輪(齒數為64)和1個齒圈構成(齒數為146),傳動比為12.5,其內部結構如圖2所示。

圖1 行星齒輪箱實驗臺
(a)
(b)
實驗共預置了太陽輪、齒圈和行星輪單個輪齒齒面磨損三種局部故障,故障程度統一設置為輪齒長度的1/2和寬度的1/2,如圖3所示。分別對正常狀態和三種故障狀態開展了實驗,采樣頻率和采樣時間分別為20 kHz和12 s,轉速設置為400、800和1 200 r/min-1,每種轉速負載設置為0、0.4、0.8和1.2 Nm,每種工況采集33個樣本。關于該實驗的更多具體信息可以參考文獻[2],此處不再贅述。
1.2 基于原始數據-DBN的診斷方法
基于原始數據的DBN診斷方法是對采集到的振動信號進行歸一化后直接輸入到DBN模型之中進行分類診斷。下面對采集到的數據進行分析:
為了與作者之前的研究成果對比,本文同樣選擇轉速為1 200 r/min、負載為1.2 Nm工況下的太陽輪故障、行星輪故障、齒圈故障和正常狀態四種狀態信號進行分析。該數據分為四種狀態,每種狀態有33個樣本,每個樣本有4列振動信號,每列信號有12×20 000=240 000個數據點。為了提高計算速度并保證診斷精度,選擇包含每個齒輪一個運轉周期的采樣點數(2 000個)作為一個訓練樣本或測試樣本,則每種狀態有3 960個樣本。采用K倍交叉驗證方法(即將所有樣本分成K份,K-1份用于訓練,1份用于測試),取K=10,則訓練樣本數為14 256個,測試樣本數為1 584個。將數據歸一化后輸入到DBN模型之中。

(a) 太陽輪

(b) 行星輪

(c) 齒圈
研究發現,對DBN分類能力影響較大的參數有三個:隱藏層數(l)、隱藏層單元數(u)和批尺寸(batchsize)(b)。對于隱藏層數,本文主要研究RBM數量為2、3、4、5這四種情況,再增加層數會導致計算量太大,意義不大。對于隱藏層單元數和批尺寸的取值目前尚未見到有明確的結論,本文經過探尋作如下設定:
(1) 隱藏層單元數
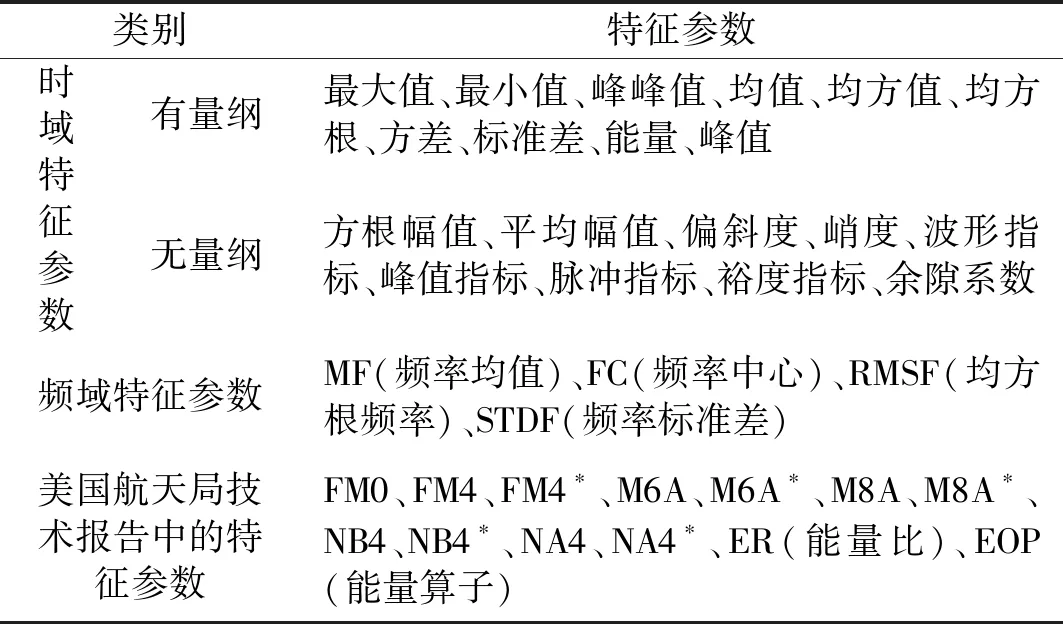
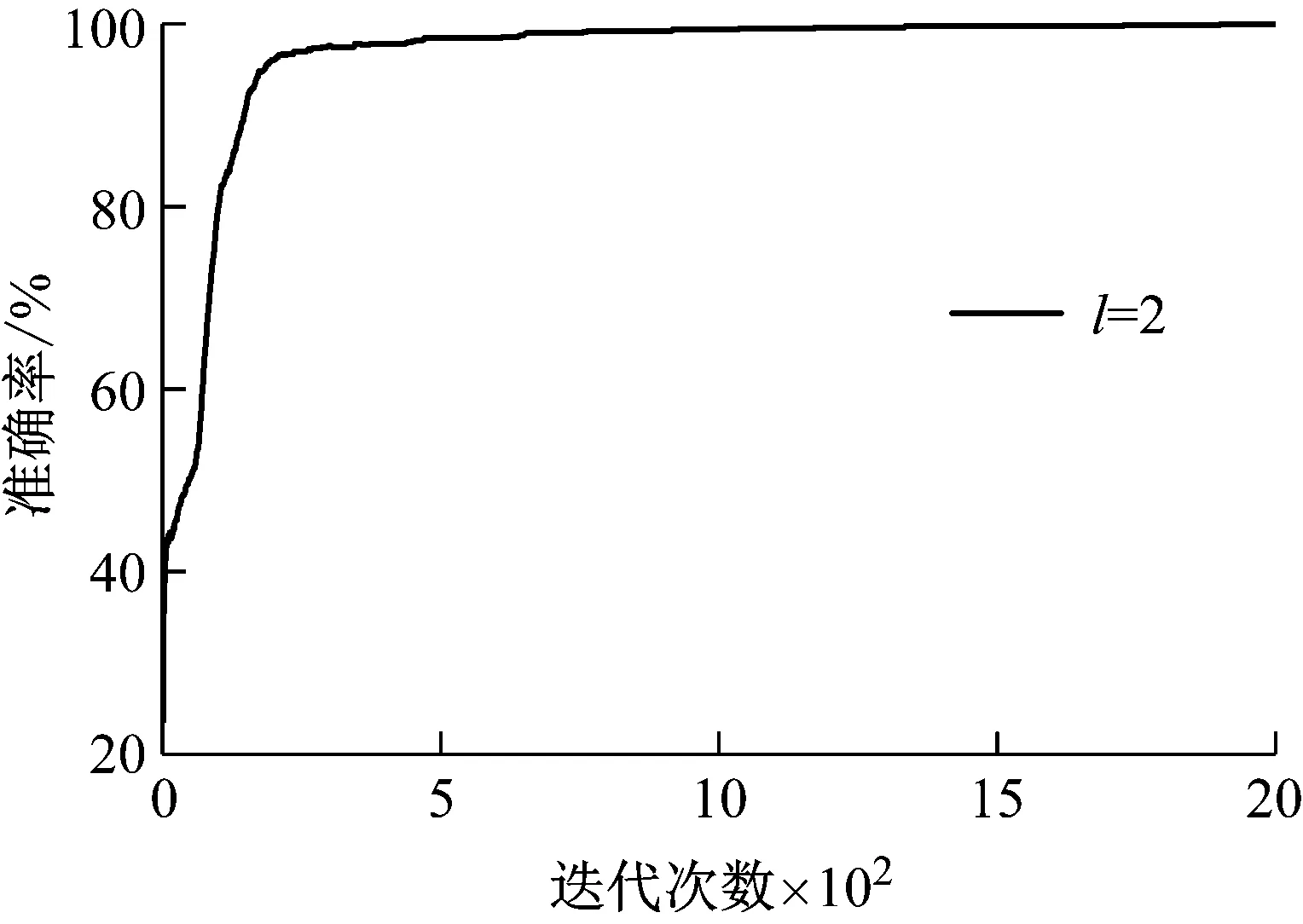
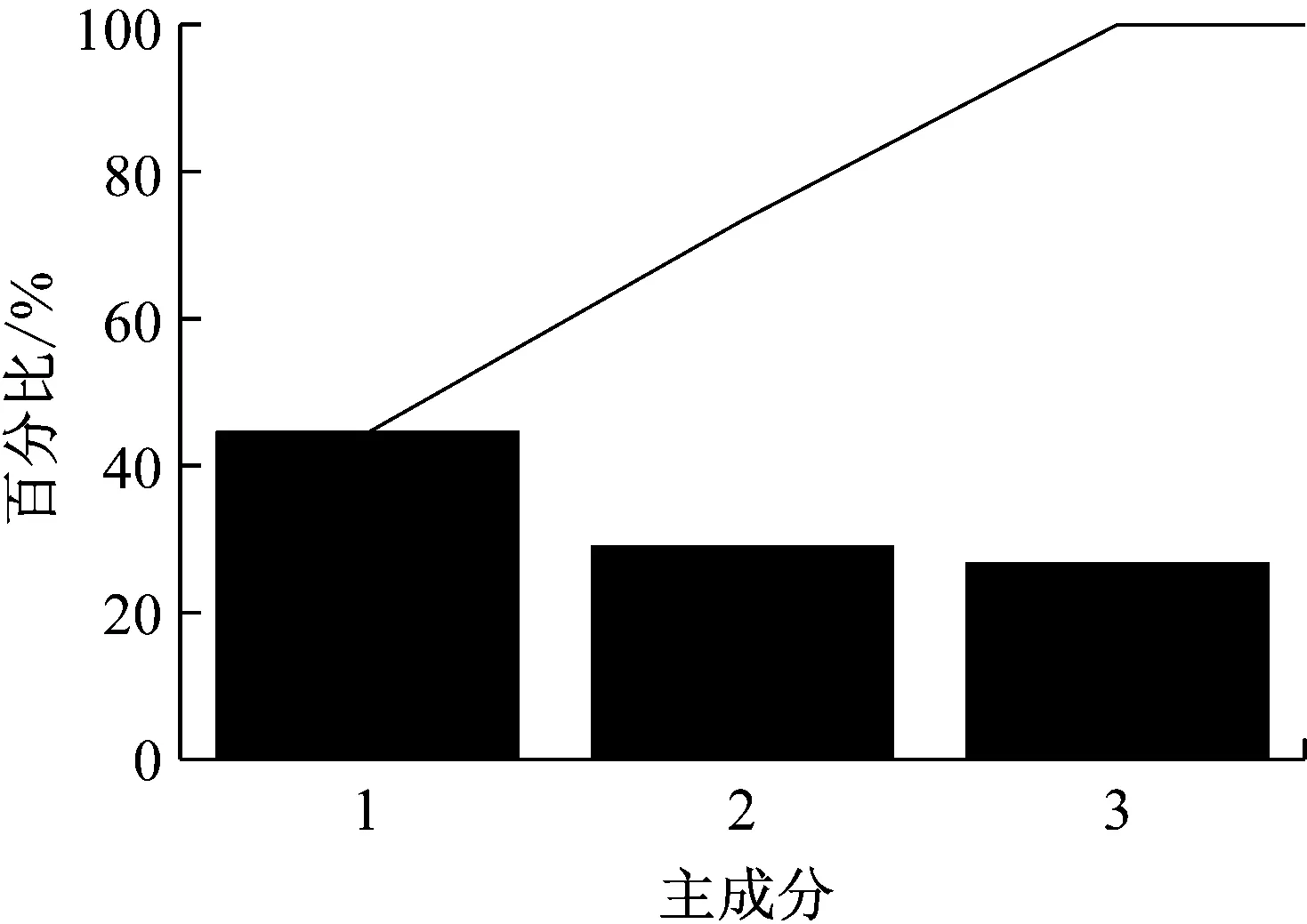
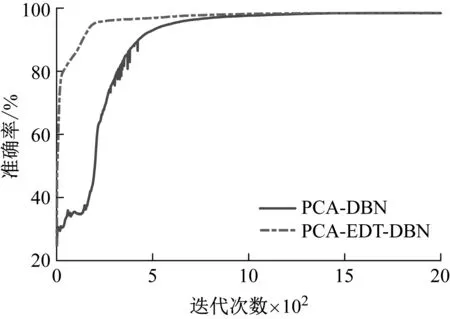
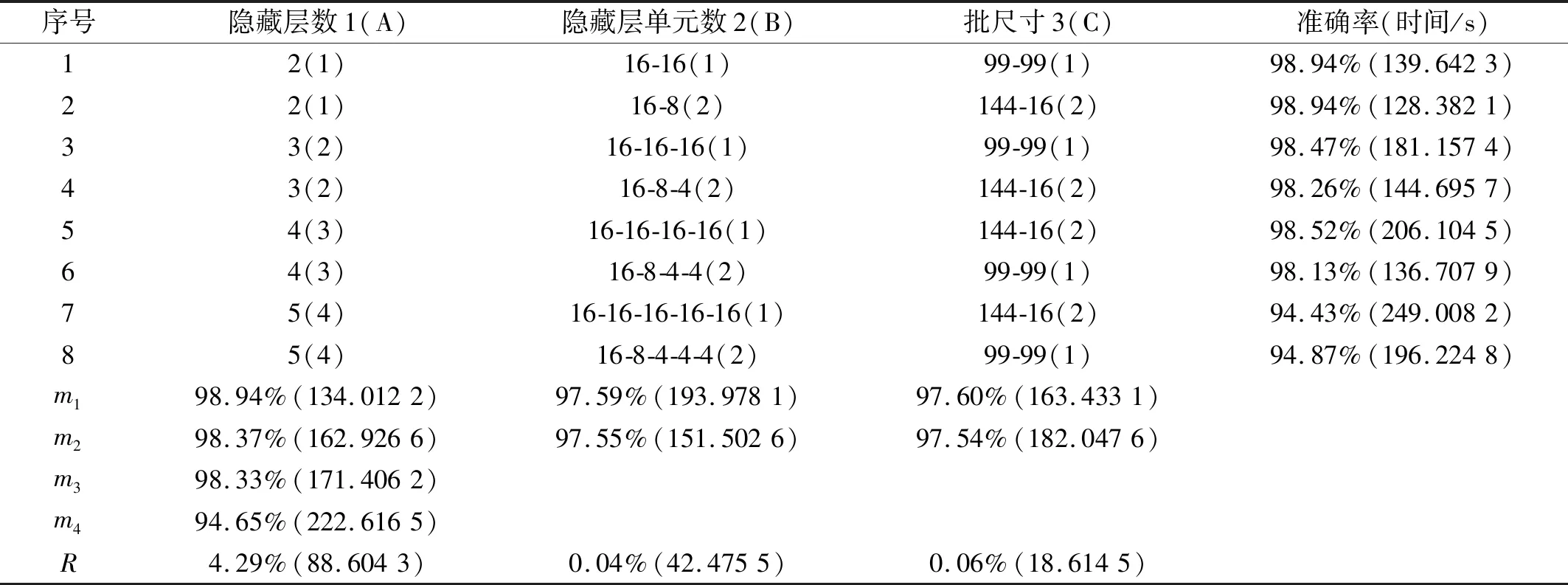
設樣本輸入數據維度為D,即輸入層單元數為D,若2N-1 例如,DBN的輸入數據維度為784,29=512<784≤210=1 024,所以N=10。則5RBM(l=5)隱藏層單元數為u1=512,u2=512,512,512,512和u1=512,u2=256,u3=128,u4=64,u5=32。 (2) 批尺寸(batchsize) 批尺寸與訓練樣本數和測試樣本數有關,本文設定為:如果訓練樣本數和測試樣本數為S1和S2,則將批尺寸定為b1=100,b2=100和b1=S1/100,b2=S2/100,樣本數若不是100的倍數則取接近值。 對于本文的數據應用,此處采用兩種計算組合來舉例說明,一是隱藏層數l=2、隱藏層節點數u1=1 024,u2=512和批尺寸b1=99,b2=99,二是隱藏層數l=3、隱藏層節點數u1=1 024,u2=512,u3=256和批尺寸b1=99,b2=99。RBM的參數設置為:將可視層與隱藏層偏置以及學習率初始值均設為0.1,初始動量設為0.5,迭代5次后,動量變為0.9。為了消除算法隨機性,每次實驗都重復10次,取10次結果的平均值。結果如圖4所示。 圖4 原始數據-DBN診斷結果 從圖中結果可以看出,對于行星齒輪箱齒面磨損故障而言,利用原始振動數據進行診斷的準確率只有25%左右。此外,由于輸入數據維度太大導致模型訓練時間特別長,兩個模型的平均訓練及測試時間分別為1.315 6×104s和1.399 3×104s。 由于每種故障都有其獨特的特征頻率,所以利用FFT將信號從時域轉換至頻域可以更好地反應各故障的自身特征,利于故障診斷。基于FFT的DBN診斷方法是在上節數據基礎上,將數據從時域轉換至頻域,從而使輸入數據維度從2 000降至1 000。在計算過程中,除各隱藏層單元數都對應降低一半之外,其余參數設置不變,對上述數據分析結果如圖5所示。從圖中結果可以看出,相對于原始時域信號作為輸入的情況,經過FFT變換至頻域信號作為輸入時診斷準確率明顯提高,迅速收斂且結果穩定,說明頻域信號代表的故障特征信息更準確、更適用于該模型。此外,訓練時間也大幅減少,基本在10 min左右,可以說效果很好,接下來的研究主要看是否可以進一步縮短計算時間。 圖5 FFT-DBN診斷結果 特征參數指表征物質或現象特性的參數信息,對傳統的智能故障診斷方法十分重要,特征參數提取和選擇的好壞關系著診斷準確率的高低。本文利用振動信號特征參數作為DBN輸入對上述數據進行診斷,提取了36個參數,見表1[13-14]。 表1 特征參數 模型參數設置以隱藏層數l=2為例,隱藏層節點數u1=32,u2=16,其它設置與前文相同,結果如圖6所示。從圖中結果可以看出,基于特征參數的DBN故障診斷方法準確率很高,約為98%,在迭代500次之后基本達到穩定。此外,模型訓練時間也大幅減少,基本在75 s左右。但是該方法前期的特征提取工作需要一定的專業性,需要花費一定的時間和人力。 圖6 特征參數-DBN診斷結果 綜上三種傳統的DBN故障診斷方法結果可以看出,采用原始數據直接作為模型輸入時,結果準確率低,訓練時間長;采用FFT變換后的信號作為模型輸入時,準確率提高了很多,訓練時間也相應減少,但仍然可以進一步降低;采用特征參數作為模型輸入時,準確率很高,訓練時間也很短,但是對專業性有一定要求。 針對上節基于DBN的傳統故障診斷方法存在診斷準確率低、訓練時間長和專業性要求高等問題,本節對本文提出的基于PCA-EDT-DBN的故障診斷方法進行研究。首先給出方法流程,然后利用與之前同樣的數據進行分析來驗證方法的有效性。 由于PCA和EDT都是比較成熟的技術,篇幅有限,本文不再對其理論進行贅述,可參考文獻[15-16]。 本文提出的基于PCA-EDT-DBN的行星齒輪箱故障診斷方法流程如圖7所示,具體步驟如下: (1) 設備運轉振動數據采集;在此步驟中需要設置多個傳感器同時采集信號以提高診斷精度,設采集到的數據樣本為xn×m,其中m為傳感器個數,n為每個傳感器采集到的數據點數。 (2) PCA數據降維;運用PCA方法分別對各個傳感器數據進行分析,根據需求取前p個主成分(通常占總成分的95%),得到PCA結果矩陣ym×p。 圖7 基于PCA-EDT-DBN的故障診斷方法流程 Fig.7 The flowchart of the fault diagnosis method based on PCA-EDT-DBN (3) 一維向量生成;一維向量由兩部分組成:第一部分是計算ym×p每兩列之間的歐氏距離,得到距離矩陣Dp×p,將矩陣中各向量自身與自身距離結果(0)去掉后按序展開得到一維向量d1×p(p-1);第二部分是將矩陣ym×p按列的順序展開成一維向量z1×mp;將兩部分組合得到最終的一維向量f1×(mp+p(p-1))=[z1×mp,d1×p(p-1)]。 (4) DBN診斷結果輸出;利用訓練數據訓練DBN,然后利用測試數據測試DBN效果給出診斷結果。在此步驟過程中,本文提出基于正交試驗設計的DBN參數優化方法來對DBN參數進行優化,結果更加理想。 數據構成及訓練樣本數和測試樣本數與3上節相同,接下來用PCA方法處理每個樣本,通過分析可知,4列信號中每列的前三個主成分即可達到占所有成分的95%以上,如圖8所示。所以取p=3,即PCA結果矩陣大小為y4×3,展開成一維向量大小為z1×12。然后計算y4×3各列之間的歐式距離得到一個3×3矩陣,去掉矩陣中各向量自身與自身距離結果(0)展開成一維向量結果為d1×6。最后將z1×12和d1×6兩部分組合得到最終的一維向量f1×18,即將樣本維度由原本2 000維降至18維。 圖8 主成分選取結果 處理好數據之后輸入到DBN模型之中,首先設置模型參數。參照1.2節參數設定,選擇隱藏層數l=3、隱藏層節點數u1=16,u2=16,u3=16和批尺寸b1=99,b2=99進行舉例分析,其它各參數設置與前文相同。同時,為了證明EDT的有效性,對沒有EDT過程的結果進行分析,即PCA-DBN方法,一維向量只為z1×12。此時的DBN參數設置為隱藏層數l=3、隱藏層節點數u1=8,u2=8,u3=8和批尺寸b1=99,b2=99,其它不變,得到結果如9所示。 在迭代2 000次之后兩種計算結果都趨于穩定,此時PCA-EDT-DBN和PCA-DBN的診斷準確率分別為98.47%和98.42%,每次計算所用平均時間分別為181.157 4 s和173.861 8 s。雖然最后的準確率相差不大,但是由圖中結果可知,PCA-EDT-DBN方法更穩定,在迭代次數或時間有限的情況下(如1 000次)效果更好。 圖9 PCA-EDT-DBN和PCA-DBN診斷結果 Fig.9 The diagnosis results of PCA-EDT-DBN and PCA-DBN 此外,本文提出利用基于正交試驗設計的DBN參數優化方法來優化DBN參數。依據1.2節設定,此處PCA-EDT-DBN方法的正交試驗因子與水平為: A:隱藏層數(l):l1=2,l2=3,l3=4,l4=5; B:隱藏層單元數(u):u1=16,u2=16,…和u1=16,u2=8,u3=4,…; C:批尺寸(b):b1=99,b2=99和b1=144,b2=16。 因此,本文定義的正交試驗設計屬于混合水平,所用正交表為L8(4124)。 表2是得到的結果,從表中結果可以看出,1、2號試驗準確率最高為98.94%,但是2號試驗計算時間要少很多,所以2號試驗(A1B2C2)比較理想。 表2 PCA-EDT-DBN正交試驗結果與分析 在得到試驗結果之后并不能依據當前最好結果確認第幾號試驗就是最優方案,因為從正交表中試驗得到的最好水平組合,在全部試驗中不一定是最優方案,可能通過分析得到的結果會找到更好的水平搭配。通常利用各因子在每一水平下結果的平均值m值和極差R來做進一步分析 mqi=∑y(Mi(qi))/qi (1) 式中:qi代表因子的水平數,i=1,2,…,r;y(Mi(qi))代表Mi因子第qi個水平所對應的結果。 極差(R)可以為各因子對最后結果的影響程度排序。一個因子的極差是該因子各水平下結果均值的最大值與最小值之差,用如下公式來計算: R=max{m1,…,mqi}-min{m1,…,mqi} (2) 進一步由m值分析之后可得,A1B2C1(隱藏層數l1=2,隱藏層單元數u1=16,u2=8,批尺寸b1=99,b2=99)組合可能準確率高且時間更短,進行試驗得到結果為98.85%(115.104 8 s),綜合考慮可能此組合更優。此外,對比R值可以發現,3個因子中A因子對準確率的影響最大,B和C因子對準確率影響不大,但是對計算時間影響很大,隱藏層單元數和批尺寸都呈現出總和越小計算時間越短的趨勢。 在作者之前的研究成果中提出了基于EMD-EDT的特征提取及故障診斷方法,該方法對轉速為1 200 r/min、負載為1.2 Nm工況下的太陽輪故障、行星輪故障、齒圈故障和正常狀態四種狀態信號故障診斷準確率為94.17%,可以說準確率也很高。但是該方法的應用涉及到很多具有專業性的信號處理技術,如TSA技術、特征提取及選擇技術等,而且EMD計算時間很長。與之相比,本文提出的基于PCA-EDT-DBN的故障診斷方法的故障診斷準確率更高、計算時間更短,而且更加智能化,即使不具備相關領域知識也可以使用,是一種無監督的故障診斷方法。 此外,為證明DBN的有效性,利用與上述數據同樣的訓練樣本訓練BP神經網絡然后用對應的測試樣本測試診斷準確率,其中BP神經網絡參數設置為:利用newff函數來創建BP神經網絡,以訓練數據來設定輸入特征的范圍,設定轉移函數為“tansig”,在輸出層選擇線性函數“purelin”,訓練函數選擇“trainlm”,迭代次數設置為1 000,展示訓練次數為10,誤差允許值為1.0×10-10,學習率設置為0.01。訓練時間用時113.024 1 s,準確率為為96.28%。雖然訓練時間比本文提出的PCA-EDT-DBN故障診斷方法稍快,但是準確率低了兩個百分點,還是可以證明DBN更有效。 本文針對基于傳統DBN故障診斷方法在行星齒輪箱故障診斷應用上結果準確率低、波動性大、耗時耗力的問題,提出了基于PCA-EDT-DBN的行星齒輪箱故障診斷方法。分析了基于原始信號、FFT和特征參數的DBN故障診斷方法的性能,給出了基于PCA-EDT-DBN的故障診斷方法的方法框架。利用行星齒輪箱齒面磨損預置故障實驗數據驗證了本文提出方法綜合性能要比傳統的DBN故障診斷方法效果好,即該方法診斷準確率高、性能穩定、訓練時間短、專業性要求低。此外,與BP神經網絡對比證明了DBN方法的有效性。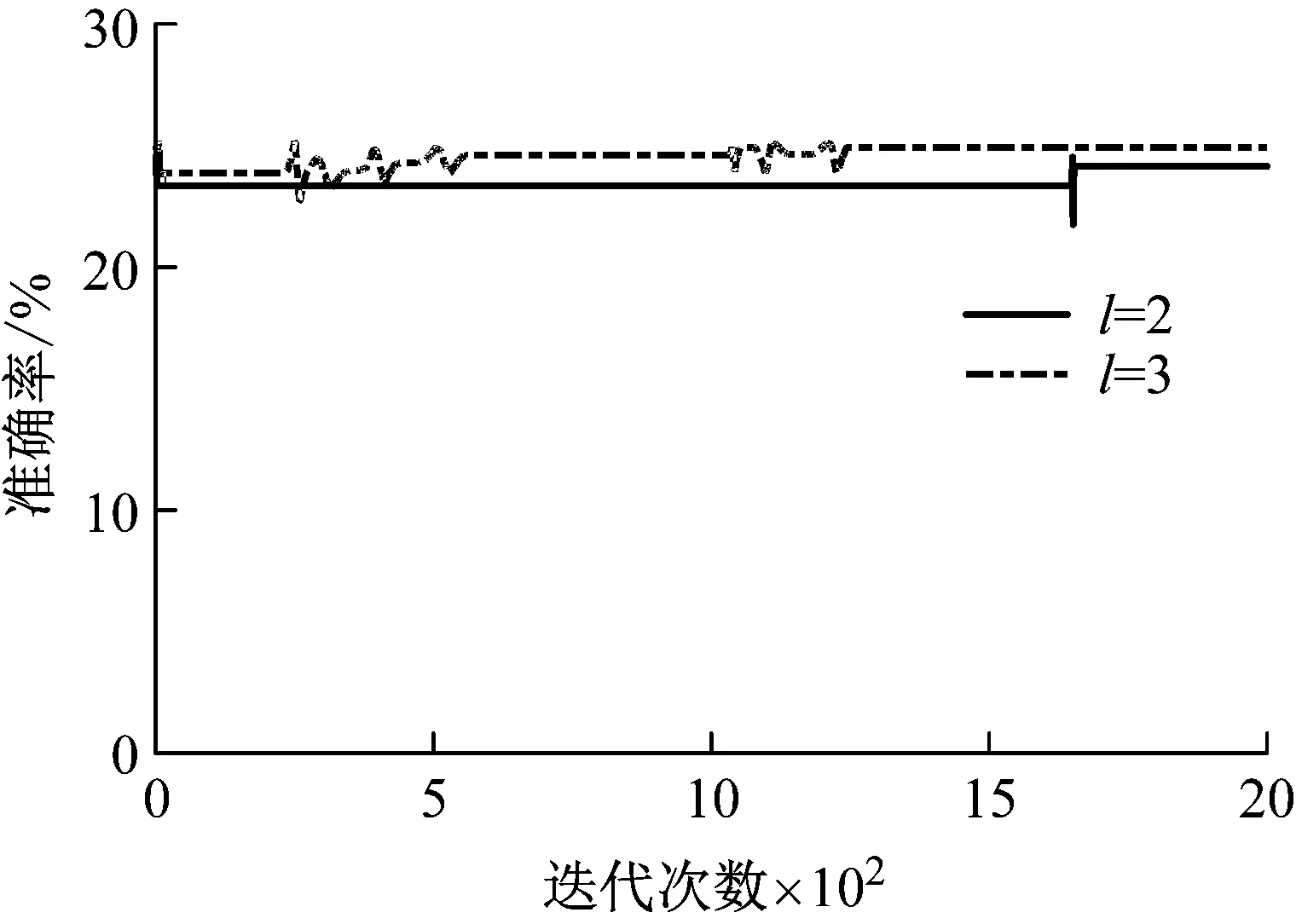
1.3 基于FFT-DBN的診斷方法
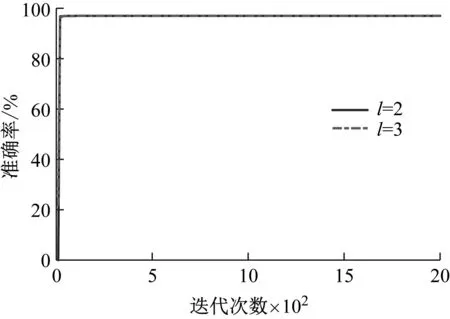
1.4 基于特征參數-DBN的診斷方法
2 基于PCA-EDT-DBN的診斷方法
2.1 方法流程

2.2 行星齒輪箱故障診斷
3 結 論

