“失之交臂”的成功
——幾道錯例剖析

龔發云

(甘肅省積石山縣積石中學 731700)

一、忽視等價性變形致錯舉例

②×2-①,6≤m≤15,③

在本題正解中能把f(1)和f(2)的范圍整體代入，避免了不等式轉化中的不等價性，從而保證了解題的正確性.

二、忽視隱含條件致錯舉例

例2(1)設m、n方程x2-2kx+k+6=0的兩個實根，則(m-1)2+(n-1)2的最小值是( ).

思路分析本例只有一個答案正確，設了3個陷阱，很容易被錯誤答案所迷惑.若利用一元二次方程根與系數的關系，易得：m+n=2k,mn=k+6,

∴(m-1)2+(n-1)2=m2-2m+1+n2-2n+1

原方程有兩個實根m、n，

∴Δ=4k2-4(k+6)≥0k≤-2或k≥3.

當k≥3時，(m-1)2+(n-1)2的最小值是8；

當k≤-2時，(m-1)2+(n-1)2的最小值是18. 顯然只有B正確.

錯誤分析上述解法忽視了m的取值范圍，所以導致了解法上的錯誤.

一般的隱含條件有：任何實數的偶次方非負，故x2≥0；三角函數中-1≤sinx≤1；指數函數ax>0;對數函數y=logax中(a>0且a≠1，且x>0)及圓錐曲線的有界性，三角形內角之和等于π等等，這些知識必須了然于胸,才會在解題中做到準確無誤，游刃有余.

三、忽視基本不等式中等號成立的條件致錯舉例

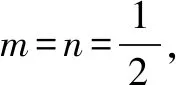
四、不注重細節致錯舉例

例4 已知數列{an}的前n項和Sn=2n+1，求an.

錯誤解法an=Sn-Sn-1=(2n+1)-(2n-1+1)=2n-2n-1=2n-1.

五、以偏概全致錯舉例

以偏概全是指思考不全面，以片面的情況，看待整體情況，而導致了解答不完整，是思維缺乏嚴謹準確性的具體表現.例如：

例5 設等比數列{an}的全n項和為Sn.若S3+S6=2S9，求數列的公比q.

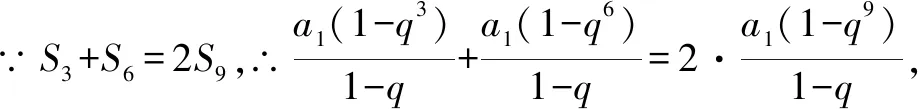
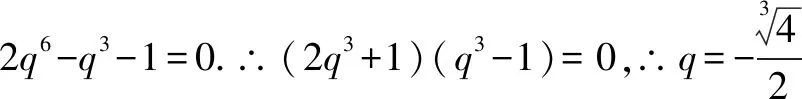
在等比數列中，a1≠0是顯然的，但公比q完全可能為1，因此，在解題時應先討論公比q=1的情況，再在q≠1的情況下，對式子進行整理變形.

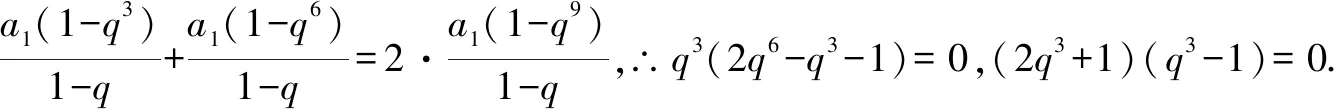
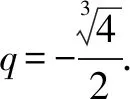
總之，要想在考試中不失分或少失分，就要針對以上情形加強平時訓練，循序漸進，有的放矢，才會有備無患，才會在做題和考試中得心應手，滿有把握.