高速飛行器瞬態熱分析及修正方法探討

呂建偉，劉 欣，蔡巧言

（中國運載火箭技術研究院，北京，100076）

0 引 言

21 世紀以來，隨著航天領域的快速發展，高速飛行器技術越來越受到世界各國關注[1]。

高速飛行器往往具有外部氣動熱環境復雜、艙內冷結構壁溫較高、外部有防熱結構散熱途徑有限、艙內設備布局緊湊且熱耗集中、以及艙內設備一體化設計導致集成度高、熱慣性小等特點，從而導致其瞬態傳熱特性十分突出[2]。為了滿足工程上對提高熱分析結果精度的迫切需求，必須開展高速飛行器瞬態熱分析及修正方法研究，解決瞬態計算影響下的熱分析結果偏差問題，從而完善熱控關鍵技術體系。

國內外學者對航天器穩態熱分析模型修正方法進行了詳盡的研究[3～6]，基本思路是首先建立試驗狀態下的熱數學模型，然后在熱平衡試驗過程中，模擬修正與熱試驗并行進行。但是從相關的國內外研究綜述來看[7]，目前的瞬態熱分析以及修正主要集中在理論方法研究。而在工程應用中，若針對整個飛行器模型修正，則需開展相關大型試驗進行驗證，因此，難以滿足工程研制過程中的進度、經費預算等實際要求。

鑒于基于隨機近似方法的模型修正方法，已被證明是目前航天器熱分析模型修正的最佳途徑[8]。因此，本文結合高速飛行器熱控系統研制過程的實際，提出首先開展敏感度分析辨識出關鍵設備及熱分析參數，然后針對該設備開展局部的單機熱試驗，修正重要的關鍵熱分析參數，從而實現不斷逼近真實結果，該方法既提高了熱分析的效率，又符合工程實際。

1 高速飛行器瞬態熱分析及修正流程

熱分析模型修正問題是已知問題結果，反向求解問題中輸入參數的過程。

作為熱分析計算時重要的輸入參數，在實際情況下，高速飛行器內、外熱源復雜且均隨時間變化，見圖1。瞬態模型的熱分析溫度中的溫升、溫降速率與熱容有較大關系，瞬態修正時要加入對熱容的修正。

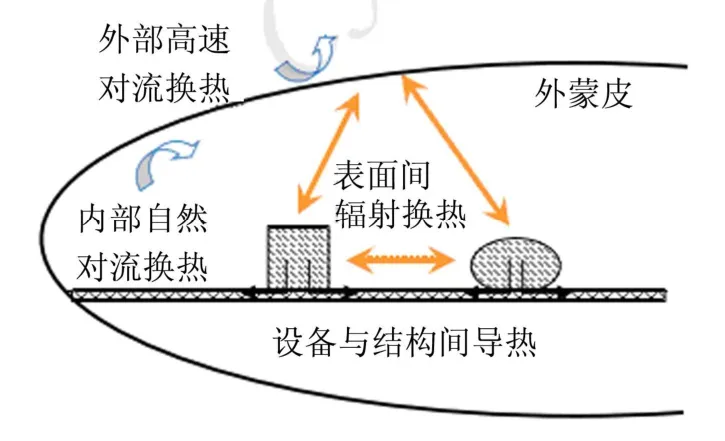
圖1 高速飛行器內外熱傳輸示意 Fig.1 Heat Transfer Inside and Outside Hypersonic Vehicle

鑒于在實際工程項目的方案論證階段，如果開展整器的熱試驗進行修正，時間和經費的消耗相對較大，因此首先必須借鑒類似的飛行器建模熱分析方法，開展關鍵影響因素的分析；然后通過設計、實施單機熱試驗，修正重要的關鍵單機及整器關鍵熱參數；最后，將修正的參數帶入整器，從而提高整器的熱分析模型修正的精度。具體的熱分析工作流程如圖2 所示。

在熱分析流程中，高速飛行器熱分析的輸入條件包括：飛行器的任務和特點，飛行器發射前環境溫度，飛行器的工作模式，飛行器結構外形及總體布局，飛行器內部儀器設備的各種安裝方式，熱物性參數及功耗，飛行器的各種材料及表面涂層特性等方面。

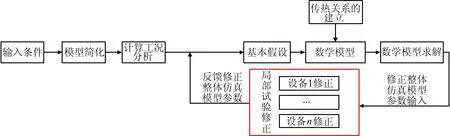
圖2 熱分析流程 Fig.2 Thermal Analysis Process

考慮高超聲速飛行器在大氣層內飛行，需要綜合考慮艙內輻射、傳導、對流等因素的影響。通常，熱網絡模型可以簡單的描述為[9]

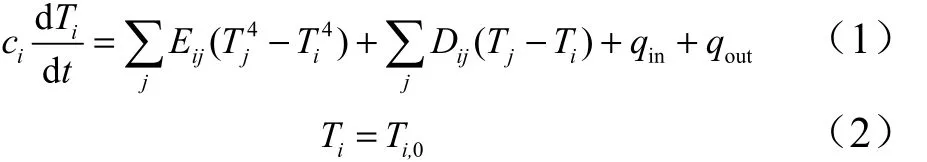
式中Ti，Tj分別為節點i 和節點j 的溫度；t 為時間；ci為節點i 的熱容；Eij為熱輻射的網絡系數；Dij為熱傳導網絡系數；qin為內熱源；qout為外熱源。

2 高速飛行器熱分析案例

在某飛行器熱分析過程中，為確保熱分析結果有效、可靠，同時，縮短研制周期并降低成本，采用局部試驗修正+整體仿真的熱分析方案。

2.1 修正設備及參數的選取

修正設備及參數的選取：指對整器熱分析而言，選取對熱分析結果影響較大的“敏感”設備；指對待修正設備而言，選取對熱分析結果影響較大的“敏感”參數。

本文修正設備的選取主要考慮：a）首次在整器應用的新研設備；b）在整器中超溫風險較大的設備。

在具體修正過程中設定兩個前提：a）所修正的參數不考慮產品受使用壽命影響的變化；b）所修正的參數不考慮產品受使用環境（如大氣壓變化等）影響產生的變化。其次，針對設備的待修正熱參數按照敏感度大小選取。

這里用統計學中的相關系數定義誤差敏感度，評價輸入傳熱參數對輸出溫度誤差的影響。具體定義如式（3）所示，其物理意義是當自變量從小到大順序變化時，對因變量相對順序的變化進行統計。

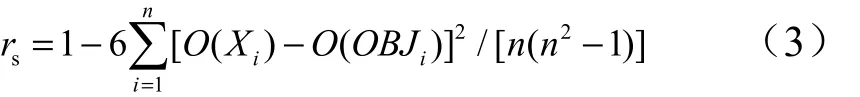
式中rs為斯皮爾曼等級相關系數；n 為抽樣次數；O(Xi)為對n 次抽樣參數值進行升序排列時，第i 次抽樣的誤差值排列序號；O(OBJi)為對n 次抽樣溫度進行升序排列時，對應第i 次抽樣得到的計算溫度誤差排列序號。以敏感度取值0.15 為劃分邊界，大于此值，傳熱參數與計算溫度誤差相關強；反之，相關較弱。

根據上述原則，以采編、慣性測量組合、發射機、中心程序器、舵機控制器、主發伺服控制器等為待修正的單機，修正的參數包括：安裝接觸熱阻、紅外發射率以及熱容參數。其中，慣性測量組合、舵機控制器是超溫風險較大設備，進行多參數修正。其它設備根據敏感性選擇修正參數，如圖3 所示，縱軸為設備待修正熱參數敏感度，橫軸為待修正設備及參數。

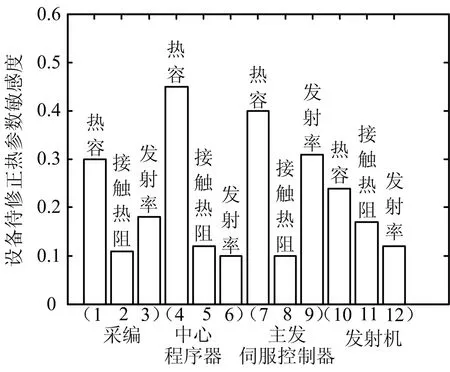
圖3 設備的敏感度分析 Fig.3 Device Sensitivity Analysis

2.2 修正參數分布

根據工程經驗修正選取參數的取值范圍和理論值以及分布情況如表1 所示。仿真計算所用的參數均按表中的理論值給定，參數取值范圍根據實際經驗在理論值附近取一個合理誤差。根據文獻[10]可知，安裝接觸熱阻、紅外發射率以及熱容等參數均服從均勻分布。

各設備修正參數的選取及分布如表1 所示。表1中理論值是指通常情況下航天器熱分析計算時所取的計算經驗參數值；真實值是本文為了衡量修正結果進行人為設計的一組值，因為實際情況下，真實值無法獲得，只能得知其在某一區間內，而在工程實際應用中，可以采用單機試驗值進行代替。有部分參數在理論值附近，但有若干參數值與理論值誤差較大，旨在評價該修正方法的有效性。

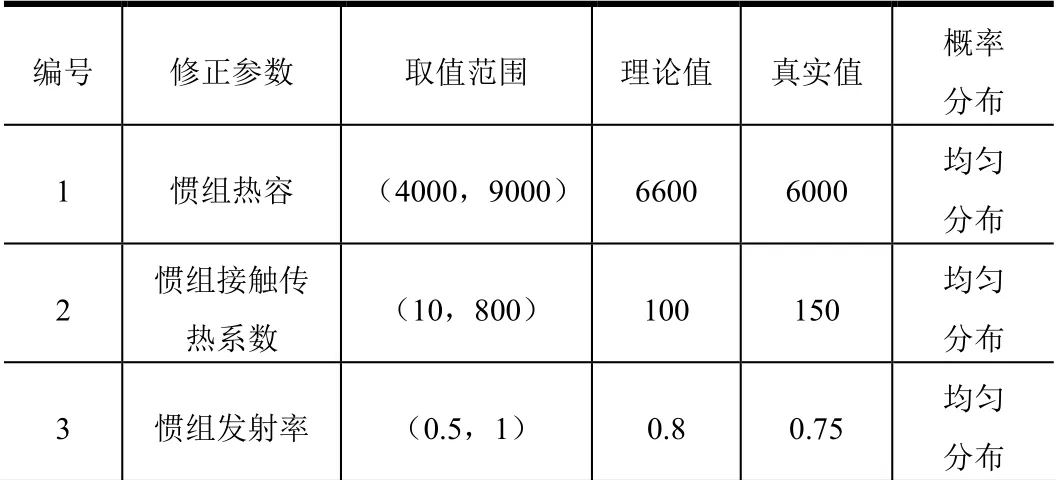
表1 設備修正參數選取及分布 Tab.l Equipment Correction Parameters Selection and Distribution

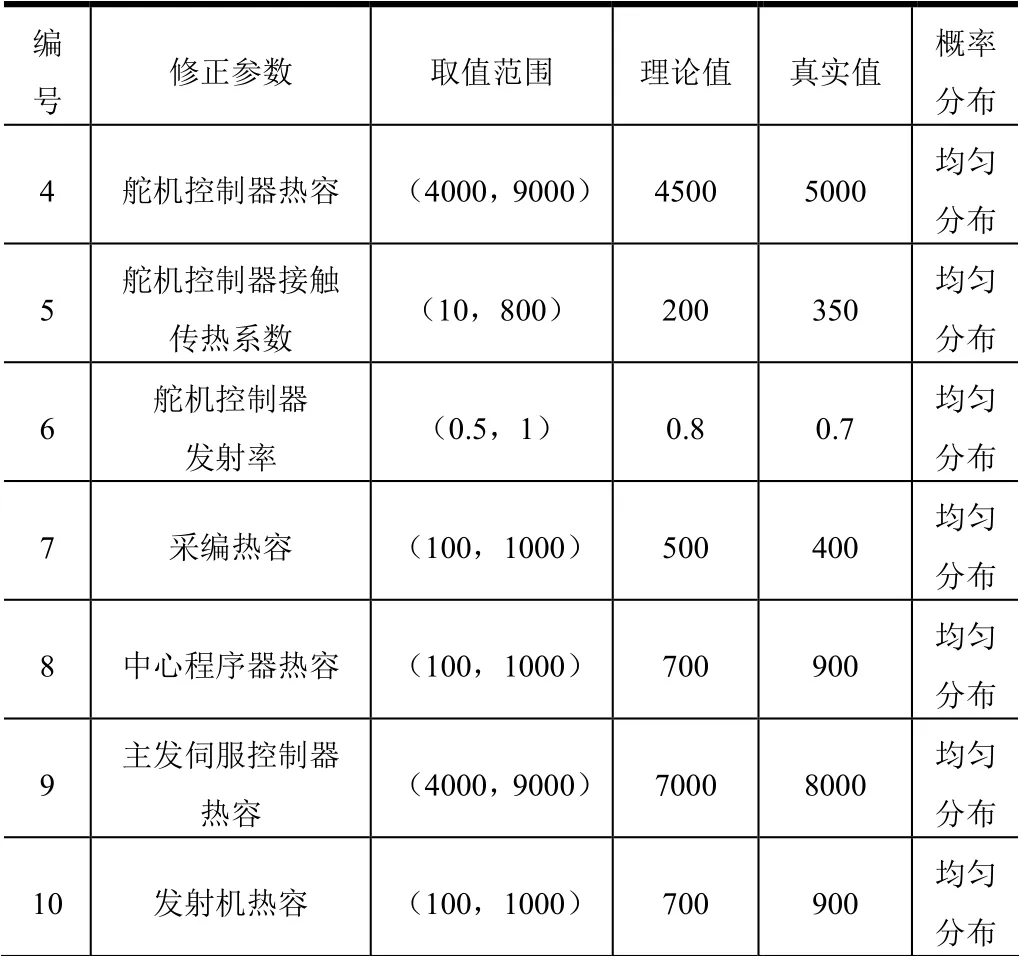
續表1

2.3 抽樣積累及概率

確定修正參數及其分布后需要對其在對應的區間內抽樣，抽樣方法選取拉丁超立方抽樣，抽樣次數為100 次，待修正參數的抽樣區間頻數統計和區間累計概率如圖4 所示。

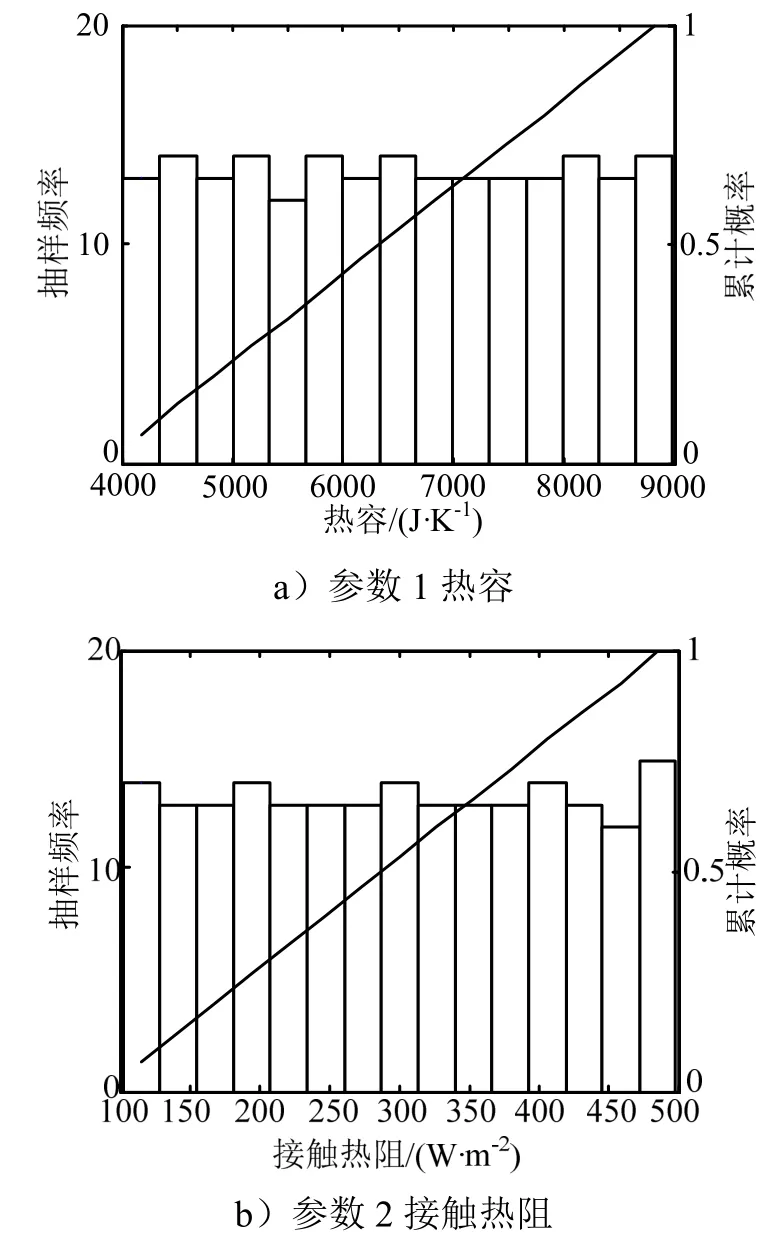
圖4 參數取值范圍 Fig.4 Parameter Range

由圖4 可知，不同的抽樣區間下抽樣頻率相當，均在14 次左右，而且累計概率接近于1，說明參數抽樣分布符合均勻分布概率模型，并且抽樣次數充足。圖4 中的累計概率說明抽樣參數服從均勻分布，與實際情況相符。

2.4 目標函數

目標函數是仿真計算溫度與試驗溫度誤差最小的一種表示，衡量了抽樣參數計算溫度與試驗溫度的“接近程度”。

在該熱分析模型中，計算公式基于均方根誤差公式，目標函數表達式為

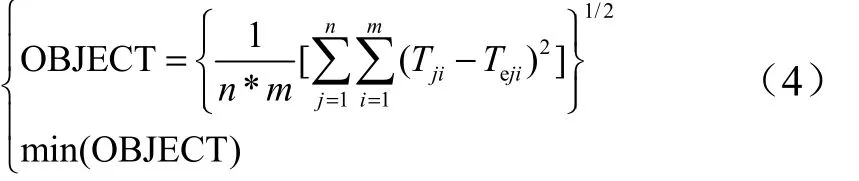
式中 j 為部件數目；i 表示離散時間點數目；Tji為第j個部件第i 個離散點的計算溫度；Teji為第j 個部件第i個離散點的試驗溫度。

為了衡量修正結果，此處試驗是指虛擬試驗，即以真實值作為輸入進行仿真計算的試驗。在工程應用中，采用單機試驗值進行代替，具體熱試驗方法如圖5 所示。

安裝板以及外殼的邊界條件可結合試驗實際情況、按照飛行器任務某個階段的設備艙瞬態溫度條件進行給定。待修正設備的幾何尺寸按照設備的真實參數給出。

圖5 設備熱試驗示意 Fig.5 Device Thermal Test Schematic

由仿真結果可知，修正模型后與試驗結果吻合較好，溫升曲線基本一致，結束時刻各設備試驗數據與仿真結果對比參見表2 所示。

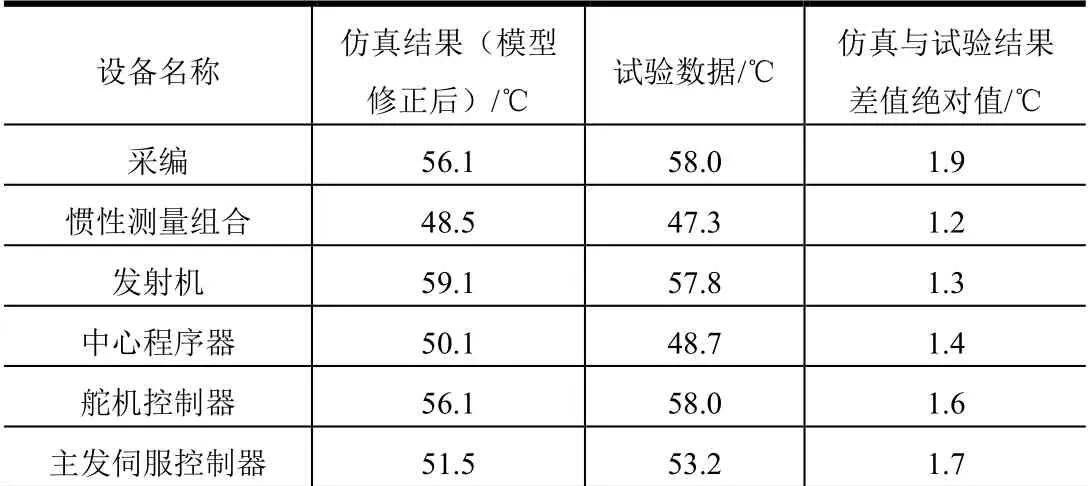
表2 仿真結果與試驗結果對比 Tab.2 Comparison of Simulation Results and Test Results

圖6 為以設備慣組為例的仿真溫度與試驗狀態下數據對比。由圖6 可見，修正后設備的溫度誤差均在2 ℃以內。

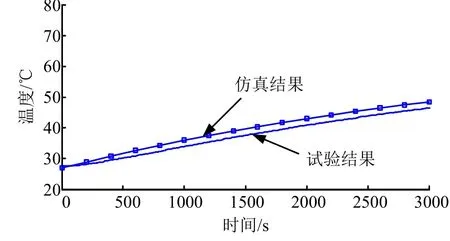
圖6 設備（以慣組為例）仿真與試驗數據對比 Fig.6 Comparison of Simulation Results and Test Results (Inertial Integrated Navigation System as an Example)

2.5 整體飛行器的修正

針對較大敏感度設備及其熱參數進行單獨修正是整體修正方法的第1 步，下面根據前面設備的修正，進行飛行器的整體修正。

按照飛行器發射場初始溫度20 ℃，飛行前準備 6 h，飛行時間1300 s，飛行后設備艙溫度邊界按熱防護層內冷結構表面溫度考慮。將6 臺設備的修正后參數帶入到飛行器整器熱分析模型中進行計算。為了驗證整體修正方法的誤差，將設備的真實值進行仿真，進行結果對比。表3 為修正前后溫度與虛擬試驗平均誤差。圖7 為修正后艙內設備溫度云圖。

表3 修正前后溫度與虛擬試驗平均誤差 Tab.3 Erro Comparion between Temperature and Virtual Test Data before and after Correction

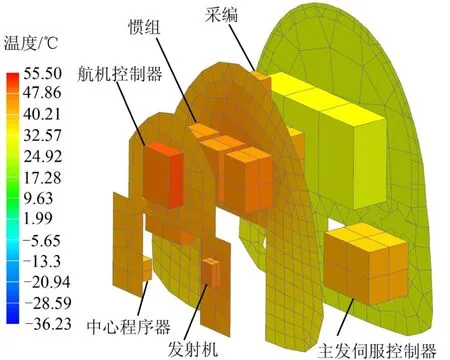
圖7 修正后艙內設備溫度云圖 Fig.7 Temperature Distribution of Revised Results

整體修正后，輸出溫度的誤差情況有了顯著的下降，雖然比設備單獨修正時的誤差略大，但是仍可以控制在3 ℃以內，可以滿足研制要求。

3 結 論

通過本文研究，可以得到以下結論:

a）本文提出的瞬態熱分析模型修正方法，從流程上可降低試驗修正參數的難度，節約了計算和試驗的工作量，為相關工程應用中的熱分析工作提供參考。

b）經對比分析，局部試驗修正后參數，仿真結果誤差最大不到2 ℃，代入后整器熱分析模型中，仿真結果的最大誤差可控制在3 ℃以內，滿足工程應用的要求。