考慮鋼梁應變強化的鋼?混組合梁抗彎承載力計算

李立峰，王孝亮，馮威，石雄偉

考慮鋼梁應變強化的鋼?混組合梁抗彎承載力計算

李立峰1, 2，王孝亮1，馮威3，石雄偉3

(1. 湖南大學 土木工程學院，湖南 長沙 410082；2. 風工程與橋梁工程湖南省重點實驗室，湖南 長沙 410082；3. 西安公路研究院，陜西 西安 710065)

采用連續(xù)強度法，考慮鋼梁應變強化作用，并基于平截面假定，對完全剪力連接的鋼-混簡支組合梁進行彈塑性分析，提出相應的抗彎承載力計算方法和公式；通過3片鋼-混簡支組合梁抗彎全過程加載試驗，掌握其彎曲破壞模式和破壞特征，同時獲得變形和應變等關鍵試驗結果；采用ABAQUS有限元軟件建立試驗梁非線性分析模型，并結合本文及其他文獻的試驗結果，對本文計算公式的精度和適用性進行驗證，理論結果與有限元分析結果、試驗結果吻合良好。研究結果表明：與規(guī)范結果相比，考慮鋼梁應變強化效應對鋼-混組合梁抗彎承載力提升7%左右，規(guī)范公式偏于保守；本文計算公式可以很好地預測完全剪力連接鋼-混簡支組合梁的抗彎承載力，可以在實際工程中應用。

鋼-混組合梁；鋼梁應變強化；抗彎承載力；模型試驗；有限元模型

鋼?混組合梁具有自重輕、力學性能好、可裝配化施工以及經(jīng)濟性高等優(yōu)點，近年來廣泛應用于橋梁、建筑等工程領域，其相關基本理論也得到深入的研究。抗彎承載力一直是鋼?混組合結構領域研究的重點，各國學者通過大量模型試驗和仿真分析，對其影響因素進行了全面分析，并相應提出了較多不同的抗彎承載力計算方法。聶建國等[1]通過理論分析建立了考慮滑移效應的組合梁抗彎承載力計算公式；Uy[2]分析總結了組合梁分別在剪力、軸力和扭矩耦合作用下的抗彎承載力計算公式；Yakel等[3]提出了相較于AASHTO規(guī)范準確性高、計算量小的簡支組合梁抗彎承載力預測方程；Gupta等[4]提出了考慮混凝土壓潰影響的密實截面簡支組合梁極限抗彎強度折減系數(shù)。劉玉擎等[5?7]國內學者也對此相關內容做了一定研究。以上研究盡管較為全面，但均忽略了鋼梁應變強化效應的影響，使得組合梁的實際抗彎承載力被低估。因此，為了合理考慮鋼梁應變強化的作用，一些國外學者在純鋼梁領域對此展開了深入的研究。Kemp等[8]根據(jù)試驗結果提出了考慮應變強化的鋼梁抗彎承載力設計公式；Manevich[9]分析了受壓鋼筋和鋼板的線形、非線性應變強化對鋼梁極限荷載的影響；Gardner等[10?11]采用連續(xù)強度法推導了考慮有、無屈服臺階鋼梁應變強化效應的抗彎承載力計算公式。相對于純鋼結構領域，關于鋼?混組合梁鋼梁應變強化的研究內容較少且尚不全面。其中， Chung等[12]采用數(shù)值模型研究了鋼梁應變強化效應對簡支鋼?混組合梁結構受力行為的作用，但未給出相應的理論計算模式；Vasdravellis等[13]率先將連續(xù)強度法應用到鋼?混組合結構領域來考慮鋼梁應變強化作用，提出了相應的抗彎承載力計算方法，而未考慮截面中性軸分布于鋼梁上翼緣和腹板內的情形，且分析基于鋼梁全截面屈服的假定，忽略了極限狀態(tài)下實際截面中性軸附近存在彈性區(qū)域的影響。因此為了綜合考慮鋼梁應變強化程度和彈塑性應力特征，本文采用連續(xù)強度法，結合彈塑性分析方法，計入鋼梁應變的強化作用，確定合理的計算模式，推導鋼?混組合梁抗彎承載力計算公式；并通過開展抗彎性能試驗，分析結構受力性能和破壞模式，匯總本文及其他文獻試驗結果對本文公式進行驗證。

1 組合梁極限抗彎承載力計算

抗彎承載力計算的關鍵是在于確定合理的截面應力分布和中性軸位置。而現(xiàn)行設計規(guī)范的鋼梁本構關系為理想彈塑性模型，未考慮鋼梁應變強化的作用；其采用的塑性分析方法忽略了極限狀態(tài)截面彈性應力分布的存在。因此，為了較為準確地反映結構的實際受力狀態(tài)，本文基于連續(xù)強度法擬建立組合梁破壞模式與截面曲率的關系，并在合理選用鋼梁材料模型的基礎上，確定考慮鋼梁應變強化程度的截面彈塑性應力分布特征，進而去獲得組合梁抗彎承載力結果。

1.1 連續(xù)強度法

Gardner[14]于2008年首先提出了一種基于構件變形能力csm/y(csm為極限荷載作用下截面外纖維極限應變，y為屈服應變)進行設計的連續(xù)強度法，最先主要用于發(fā)生屈曲破壞的純鋼梁結構，通過建立截面長細比與非彈性局部屈曲變形能力之間的連續(xù)關系確定csm，并采用彈塑性的材料強化模型，確定其進入應變強化階段的程度，從而合理考慮了金屬材料應變強化的影響。而推廣至正彎矩作用的密實截面組合梁，其csm可直接通過彎曲破壞時的極限應變確定，因而相對鋼梁得到了一定的簡化。

1.2 基本假定

本文分析模型基于以下假定：

1) 鋼?混組合梁為完全剪力連接，界面間無黏結滑移，沿梁高應變分布符合平截面假定；

2) 鋼梁本構關系采用雙線性隨動強化材料模型(圖1)，其中sh=/100(和sh分別為鋼梁彈性階段和強化階段的彈模)，混凝土翼緣板達到受壓極限狀態(tài)時截面應力呈矩形分布，應力為0.85cd(cd為混凝土軸心抗壓強度)；

3) 鋼梁下翼緣處應變已進入強化階段；

4) 忽略混凝土受拉強度的影響；

5) 忽略混凝土板內橫向和縱向鋼筋的作用。

圖1 鋼梁雙線性隨動強化材料模型

1.3 分析流程

基于上述基本假定，首先假定組合梁破壞模式由混凝土控制，并確定極限狀態(tài)下截面曲率，在初設截面中性軸位置的基礎上，進一步得到截面應變和應力分布，分別計算截面各關鍵受力區(qū)域的內力大小，由力平衡方程確定中性軸位置，并對初設內容(包括中性軸位置和破壞模式)進行驗證或調整，最終得到考慮鋼梁應變強化的抗彎承載力，具體分析流程如圖2所示。

1.4 截面幾何參數(shù)和力學參數(shù)

圖3~5給出了組合梁截面的幾何參數(shù)和應變應力分布的力學參數(shù)，其中eff和c分別為混凝土翼緣有效寬度和厚度；a為鋼梁的高度；f1和f1分別為鋼梁上翼緣的寬度和厚度；f2和f2分別為鋼梁下翼緣的寬度和厚度；w和w分別為鋼梁腹板的高度和厚度。此外，y為鋼梁屈服應力；ft和fb為極限狀態(tài)鋼梁上、下翼緣中心處應變；wt和wb為極限狀態(tài)鋼梁腹板頂、底部應變；s為截面中性軸距混凝土頂板的距離；y為鋼梁腹板剛出現(xiàn)屈服時距腹板頂部的彈性高度。

圖2 抗彎承載力分析流程圖

圖3 組合梁中性軸在混凝板內截面應變和應力分布

圖4 組合梁中性軸在鋼梁上翼緣內截面應變和應力分布

圖5 組合梁中性軸在鋼梁腹板截面應力應變分布

1.5 破壞模式與曲率確定

純彎狀態(tài)下，完全剪力連接鋼?混組合梁的破壞形態(tài)為典型的彎曲破壞模式，分為混凝土板壓潰、或者鋼梁下翼緣受拉破壞2種。基于平截面假定，分別以c和a為混凝土和鋼梁外纖維極限應變對應的截面曲率，s,c和s,a分別對應組合梁由混凝土和鋼梁控制破壞時截面中性軸距混凝土頂板的距離。混凝土極限壓應變按我國《混凝土結構設計規(guī)范》(GB 50010—2010)[15]規(guī)定取cu=0.003 3；考慮鋼材延展性要求，根據(jù)歐洲規(guī)范Ⅲ《EN 1993?1 ?1》[16]規(guī)定鋼材極限拉應變u=15y。

為了確定組合梁的破壞模式，可先假定組合梁為混凝土壓潰破壞，在平截面假定基礎上，將分析獲得的鋼梁底緣最大拉應變a,max與鋼梁達到延展性極限時的應變au相比較即可。若a,max≤au，則組合梁破壞模式由混凝土控制；若a,max>au，則破壞模式由鋼梁控制。

1.6 截面彈塑性分析及公式推導

彈塑性分析是一種計算截面抗彎承載力相對有效、準確和方便的方法，本文采用此方法分別針對截面中性軸在混凝土板、鋼梁上翼緣和腹板內3種情形展開公式推導。

1.6.1 截面中性軸在混凝土板內

由截面應變分布可獲得截面各關鍵位置處應變，如式(5)~(8)所示。

1)混凝土翼緣板處內力c和相對于中性軸的彎矩c如式(9)~(10)所示。

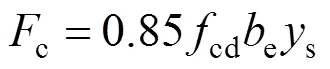
2) 鋼梁上翼緣處內力ft和相對于中性軸的彎矩ft如式(11)~(13)所示。

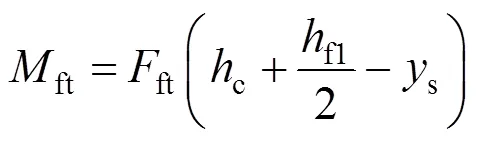
3) 鋼梁腹板處內力w和相對于中性軸的彎矩w如式(19)~(20)和式(23)~(24)所示。

其中：w可分解為圖3(b)中4個部分，其各自分力為w1~w4，如式(15)~(18)所示。

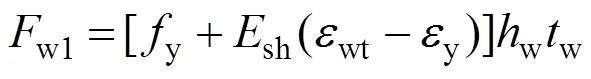
4) 鋼梁下翼緣處內力fb和相對于中性軸的彎矩fb如式(25)~(26)所示。

1.6.2 截面中性軸在鋼梁上翼緣內

截面中性軸在鋼梁上翼緣內時，由于上翼緣厚度較小，中性軸與上翼緣的頂?shù)装寰嚯x較短，因此，可以假定鋼梁上翼緣應力處于彈性階段。

由截面應變分布可獲得截面各關鍵位置處應變，鋼梁頂板上、下邊緣應變ft1和ft2見式(27)~ (28)，而wt，wb和fb仍可由式(6)~(8)確定。

1) 混凝土翼緣板處內力c和相對于中性軸的彎矩c如式(29)~(30)所示。

2) 鋼梁上翼緣處內力ft和相對于中性軸的彎矩ft如式(31)~(32)所示。

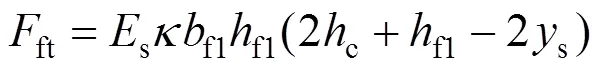
3) 鋼梁腹板處內力w和相對于中性軸的彎矩w與圖3(b)計算模式一致，可由式(14)~(20)確定。

4) 鋼梁下翼緣處內力fb和相對于中性軸的彎矩fb與圖3(a)計算模式一致，可由式(25)~(26) 確定。

1.6.3 截面中性軸在鋼梁腹板

由截面應變分布可獲得截面各關鍵位置處應變，ft和wt見式(33)~(34)，而wb和fb仍可由式(7)~(8)確定。

1) 混凝土翼緣板處內力c和相對于中性軸的彎矩c與圖4中一致，由式(29)~(30)確定。

2) 鋼梁上翼緣處內力ft和相對于中性軸的彎矩ft可仍由式(11)~(13)確定。

3) 鋼梁腹板處內力w和相對于中性軸的彎矩w如式(40)~(41)、式(44)~(45)所示。

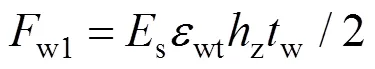
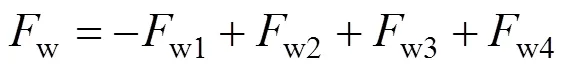
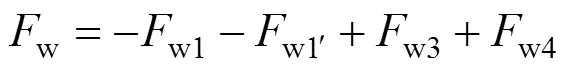
4) 鋼梁下翼緣處內力fb和相對于中性軸的彎矩fb可仍由式(25)~(26)確定。

1.7 極限抗彎承載力

組合梁極限狀態(tài)下截面中性軸位置s可根據(jù)截面內力平衡方程確定，其中式(34)可獲得中性軸在混凝土板和鋼梁上翼緣內情形下的中性軸位置，式(35)可獲得中性軸在鋼梁腹板內情形下的中性軸位置。

在確定中性軸位置后，考慮鋼梁應變強化的組合梁極限抗彎承載力csm可由式(48)確定。

2 模型試驗

為驗證本文公式的正確性，設計3根完全剪力連接鋼?混簡支組合梁的抗彎性能試驗，在確定鋼?混組合梁受力性能和破壞形態(tài)的基礎上，分析鋼梁應變強化效應對極限抗彎承載力的影響。

2.1 試件制作

試驗梁B1~B3跨徑分別為2.5，3.0和4.0 m，截面尺寸均一致，翼緣板寬、厚分別為700 mm和70 mm，鋼梁高為268 mm，截面及鋼筋布置如圖6所示。栓釘橫向雙排間距為60 mm，直徑為13 mm，采用ML-15AL型號鋼材。混凝土板內配置上下兩排鋼筋，鋼筋規(guī)格為HRB400，直徑均為8 mm，縱向間距為130 mm。

單位：mm

2.2 材料參數(shù)

混凝土板采用C50配合比澆筑，鋼梁選取Q345qd鋼材，獲得相關材料參數(shù)如表1所示。

表1 本文試驗梁材料參數(shù)

2.3 加載及測試方案

試驗梁B1~B3均采用1 500 kN液壓千斤頂通過分配梁進行兩點彎曲加載，其純彎段均1.0 m。本試驗針對跨中位移、縱向應變、裂縫分布、試驗荷載等關鍵內容進行測試和記錄，試驗梁加載立面圖及測點布置如圖7所示。

圖7 試驗梁加載立面圖及測點布置

2.4 試驗結果

2.4.1 破壞現(xiàn)象和荷載-位移曲線

3片試驗梁的彎曲破壞現(xiàn)象和受力特征基本一致。在初期荷載作用下，跨中位移增加緩慢，結構剛度處于彈性階段。荷載增加至0.4~0.5u(u為試驗梁極限荷載)時，跨中混凝土板底緣出現(xiàn)第一條裂縫，跨中鋼梁底板屈服。直至荷載達到0.85u左右后，裂縫數(shù)量大幅增加，混凝土板受壓區(qū)高度逐步減小，結構剛度隨荷載增加顯著降低。最終在極限荷載作用下，試驗梁由于混凝土跨中處出現(xiàn)局部壓潰而破壞。試驗梁破壞現(xiàn)象見圖9。

圖8 試驗圖片

圖9 試驗梁典型彎曲破壞現(xiàn)象

從圖10中荷載?跨中位移曲線可知，隨著試驗梁高跨比的增加，結構的剛度和極限荷載隨之增大，但跨中截面的極限抗彎承載力基本一致。

圖10 荷載-跨中位移曲線

圖11 跨中截面混凝土頂板荷載-應變曲線

2.4.2 荷載-應變曲線

圖11~12分別給出了試驗梁跨中處混凝土頂板和鋼梁底板荷載?應變曲線。結果顯示，3片梁的混凝土頂板壓應變均達到了0.003 3，滿足混凝土被壓潰的條件；鋼梁底板拉應變在達到0.5u后，基本已進入強化階段，而在極限狀態(tài)時試驗梁的鋼梁底板平均應變達到了14 000 με，小于鋼材延展性極限應變15y=28 030 με。根據(jù)1.5節(jié)判定規(guī)則，可知本文試驗梁破壞模式均為混凝土壓潰破壞。

圖12 跨中截面鋼梁下翼緣荷載-應變曲線

3 仿真分析

3.1 模擬方式

本文采用ABAQUS軟件建立各試驗梁的非線性有限元模型。其中，混凝土翼緣板、加載和支承處鋼墊板采用實體單元C3D8R模擬，鋼梁和加勁肋均采用C3D8I單元模擬，翼緣板內鋼筋采用桁架單元T3D2模擬；栓釘連接件選用了非線性彈簧單元模擬，并賦予其非線性荷載?滑移關系。鋼筋嵌入混凝土板中，加勁肋、墊板與鋼梁均綁定連接，鋼混界面間接觸的作用通過硬接觸和設置罰函數(shù)來模擬。混凝土單軸受壓、受拉本構關系曲線采用規(guī)范[15]規(guī)定的理論公式，鋼材本構如圖1所示。

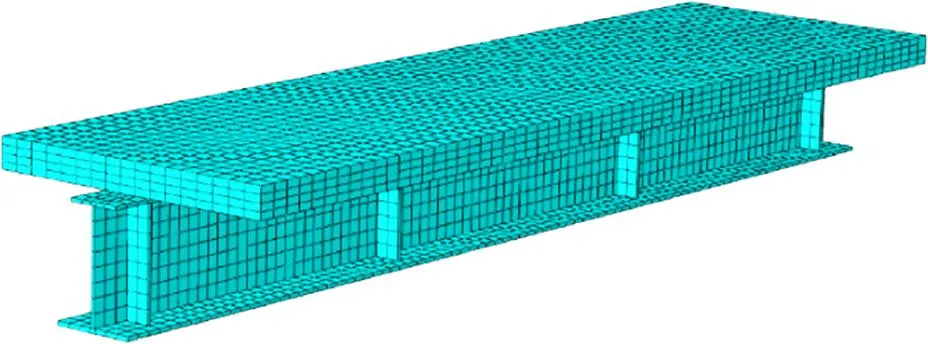
圖13 有限元模型網(wǎng)格圖

3.2 結果對比

圖14為3根梁有限元計算結果與試驗結果的荷載?位移曲線對比。

圖14 有限元和試驗荷載-位移曲線對比

可以看出，有限元模型的荷載?位移曲線與試驗的結果在起始剛度、極限強度和總體走勢上具有較高的吻合度，其中試驗梁B1~B3的有限元計算的極限荷載與試驗結果比值的均值和標準差分別為0.975和0.01，其誤差較小。說明本文建立的非線性有限元模型能有效地模擬組合梁考慮鋼梁應變強化的彎曲受力全過程。

4 公式驗證與適應性用性討論

為了驗證本文抗彎承載力計算公式的精度和適用性，對本文和文獻[17]共12根密實截面完全剪力連接試驗梁，分別采用本文公式和歐州規(guī)范Ⅳ[18]計算相應的抗彎承載力結果csm和code，并與試驗結果test進行對比，如表2所示。

其中，本文試驗梁采用規(guī)范和本文方法的計算值與試驗值的比值分別為0.893和0.963；文獻[17]進行了9根組合梁的抗彎試驗，采用規(guī)范和本文方法的計算值與試驗值的比值分別為0.926和0.983。

可以看到鋼梁應變強化效應可以顯著提升組合梁抗彎承載力達7%左右，規(guī)范計算結果相對實測值低估了7%~10%，而本文方法對純彎狀態(tài)組合梁抗彎承載力的計算結果與試驗結果整體吻合良好，具有較高的準確性。

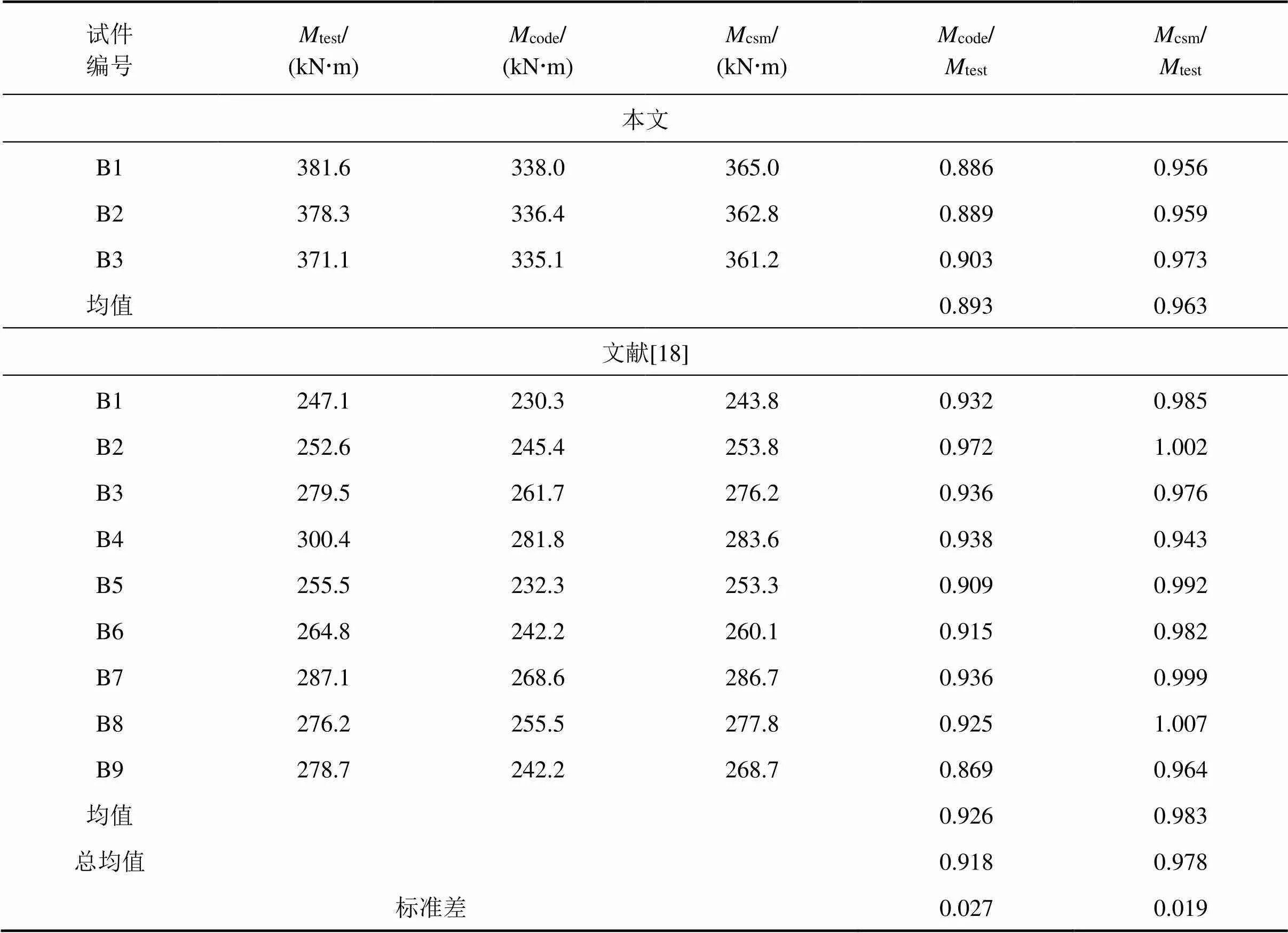
表2 本文計算公式與規(guī)范、試驗結果對比

5 結論

1) 鋼混組合梁抗彎承載力采用現(xiàn)行規(guī)范設計雖然簡化了計算，但由于忽略了鋼梁應變強化效應，使得計算結果較為保守，相對實測值低估了7%~10%。

2) 本文公式物理概念明確，可以較為真實地確定極限狀態(tài)截面彈塑性應力分布和應變強化效應的特點，預測完全剪力連接組合梁的極限抗彎承載力具有較高精度，對實際工程設計提供了一定的參考價值。

[1] 聶建國, 沈聚敏. 滑移效應對鋼?混凝土組合梁彎曲強度的影響及其計算[J]. 土木工程學報, 1997(1): 31?36. NIE Jianguo, SHEN Jumin. Effect of slip effect on bending strength of steel-concrete composite beams and its calculation[J]. Journal of Civil Engineering, 1997(1): 31?36.

[2] Uy B. Applications, Behaviour and design of composite steel-concrete structures[J]. Advances in Structural Engineering, 2012, 15(9): 1559–1571.

[3] Yakel A, Azizinamini A. Improved moment strength prediction of composite steel plate girders in positive bending[J]. Journal of Bridge Engineering, 2005, 10(1): 28?38.

[4] Gupta V K, Okui Y, Inaba N, et al. Effect of concrete crushing on flexural strength of steel-concrete composite girders[J]. Structural Engineering/Earthquake Engineering, 2007, 24(2): 73s?83s.

[5] YANG Fei, LIU Yuqing, Xin Haohui. Positive bending capacity prediction of composite girders based on elastoplastic cross-sectional analysis[J]. Engineering Structures, 2018(167): 327?339.

[6] SU Qingtian, ZENG Minggen, DAI Changyuan, et al. Bending capacity of orthotropic composite bridge deck with T-shaped steel ribs[C]// IABSE Symposium Report International Association for Bridge and Structural Engineering, 2016, 106(13): 70?76.

[7] 王春生, 朱經(jīng)緯, 翟曉亮, 等. 雙管翼緣鋼-混凝土新型組合梁抗彎性能試驗[J]. 中國公路學報, 2017, 30(3): 147?158. WANG Chunsheng, ZHU Jingwei, ZHAI Xiaoliang, et al. Flexural behavior experiment of steel and concrete composite girder with double tubular flange[J]. Chinese Journal of Highway and Transport, 2017, 30(3): 147?158.

[8] Kemp A R, Byfield A R, Nethercot D A. Effect of strain hardening on flexural properties of steel beams[J]. The Structural Engineer, 2002, 80(8): 188?197.

[9] Manevich A I. Effect of strain hardening on the buckling of structural members and design codes recommendations [J]. Thin-Walled Structures, 2007, 45(10): 810?815.

[10] Gardner L, Wang F, Liew A. Influence of strain hardening on the behavior and design of steel structures[J]. International Journal of Structural Stability & Dynamics, 2011, 11(5): 21.

[11] YUN X, Gardner L, Boissonnade N. The continuous strength method for the design of hot-rolled steel cross-sections[J]. Engineering Structures, 2018(157): 179?191.

[12] Chung K, Chan C. A numerical investigation into the effect of strain hardening on the structural behaviour of simply supported composite beams[C]// Pacific Structural Steel Conference, Beijing, 2010.

[13] Vasdravellis G, Kucukler M, Macorini L. Deformation-based design of composite beams[J]. Composite Construction in Steel and Concrete VII, 2016(131): 1?14.

[14] Gardner L. The continous strength method[J]. Proceedings of the ICE-Structures and Buildings, 2008, 161(3): 127?33.

[15] GB 50010—2010, 混凝土結構設計規(guī)范[S]. GB 50010—2010, Specification for design of concrete structures[S].

[16] Eurocode 3: Design of Steel Structures-Part 1.1: General rules and rules for buildings[S].

[17] 聶建國, 唐亮. 密實截面組合梁的豎向抗剪強度Ⅰ:受正彎矩作用的組合梁[J]. 土木工程學報, 2008, 41(3): 7?14. NIE Jianguo, TANG Liang. Vertical shear strength of compacted composite beams Ⅰ: Composite beams subjected to positive bending moment[J]. Journal of Civil Engineering, 2008, 41(3): 7?14.

[18] EN 1994-2. Eurocode 4: Design of composite steel and concrete structures-Part Ⅱ: General rules and rules for bridges[S].

Calculation of flexural capacity of steel-concrete composite beams considering strain strengthening of steel beams

LI Lifeng1, 2, WANG Xiaoliang1, FENG Wei3, SHI Xiongwei3

(1. College of Civil Engineering, Hunan University, Changsha 410092, China;2. Key Laboratory for Wind and Bridge Engineering of Hunan Province, Changsha 410082, China; 3. Xi’an Highway Institute of the Shaanxi Province, Xi’an 710065, China)

In this paper, the continuous strength method was adopted to consider the strain strengthening effect of steel beam, and based on the assumption of plane section, the elastic-plastic analysis of steel-concrete simply supported composite beam with full shear connection was carried out, and the corresponding calculation method and formula of flexural capacity were put forward. The bending failure mode and failure characteristics of three pieces of steel-concrete composite test beams have been mastered and the key test results such as deformation and strain have been obtained at the same time. The nonlinear analysis model of the test beam was established by using the ABAQUS finite element software. The accuracy and applicability of the formula in this paper were verified by combining the experimental results of this paper and other literatures, and the results of theory calculation were in good agreement with the results of the finite element analysis and experiment. The results show that Compared with the results of the code, considering the strain strengthening effect of steel beam, the flexural capacity of steel-concrete composite beam is increased by about 7%, and the criterion formula is conservative. The formula proposed in this paper can well predict the flexural capacity of steel-concrete simply supported composite beams with full shear connections, and can be applied in practical engineering.

steel-concrete composite beam; strain strengthening of steel beam; flexural capacity; model test; finie element model

U448.216

A

1672 ? 7029(2019)11? 2822 ? 10

10.19713/j.cnki.43?1423/u.2019.11.023

2019?01?31

國家自然科學基金資助項目(51978257)；陜西省交通廳科研課題資助項目(17-19K)；云南省交通廳科研課題資助項目(2017-104)

李立峰(1971?)，男，湖南沅江人，教授，博士，從事橋梁抗震、超高性能混凝土應用、鋼橋與鋼混組合橋基本理論等研究；E?mail：lilifeng@hnu.edu.cn

(編輯 蔣學東)