隧道應力擾動區及其影響因素分析

何洵，李鈾

隧道應力擾動區及其影響因素分析

何洵，李鈾

(中南大學 土木工程學院，湖南 長沙 410075)

一般認為擾動區范圍為隧道截面最大直線尺寸的3~5倍。在彈性狀態下進行分析，利用已有的未考慮自重的圓形隧道解析解確定圓形隧道擾動區影響因素及擾動區范圍，并總結出圓形隧道擾動區半徑與隧道半徑和泊松比之間的多項式關系。采用ANSYS分析考慮自重的圓形、直墻半圓拱和矩形3種截面隧道開挖后圍巖應力場和擾動區范圍。應用彈塑性折線理論將彈性狀態所得的成果推廣至彈塑性狀態。研究結果表明：圓形、矩形、直墻半圓拱3種截面形式的最大擾動區范圍均超出了隧道截面最大直線尺寸的5倍，即一般情況下大于現時認為的3~5倍；從減小擾動區范圍的角度出發，相同高度與跨度的3種隧道截面，圓形截面最優，直墻半圓拱截面次之，矩形截面最差。研究成果可為隧道支護設計以及數值模型計算域的選取提供參考。

圓形隧道；圍巖；應力擾動區；數值模擬；彈塑性分析

地下洞室開挖將引起應力重分布，開挖后巷道周圍應力發生顯著變化，而遠場應力基本保持不變。通常認為開挖前后應力變化小于5%的區域沒有受到開挖影響，并稱這一區域的巖體為原巖；而變化大于5%的區域是開挖影響區，并稱為擾動 區[1]。目前，擾動區范圍一般認為是“井巷或采場最大直線尺寸的3~5倍”，對隧道而言，就是隧道橫截面最大直線尺寸(后面簡稱為隧道最大直線尺寸)的3~5倍。擾動區范圍直接影響隧道穩定性分析和支護設計，眾多學者在這方面進行了研究。周輝等[2]研究了深井巷道圍巖擾動應力場與開挖擾動區之間的關系。并且利用 FLAC3D進行數值模擬分析，得到了水平應力、垂直應力、最大主應力、最小主應力的變化規律與相互之間的聯系，分析了深井巷道掘進過程中圍巖擾動應力場的演化特征。趙維生[3]等對垂直交岔點圍巖穩定性以及開挖擾動后圍巖主應力展開研究，結果表明擾動后主應力主要受到原巖應力的影響，而基本不受交岔點與地應力空間位置和巷道開挖順序的影響。唐禮忠等[4]針對冬瓜山銅礦深部出礦巷道其復雜的賦存條件和“高應力+動力擾動”的應力環境，利用ABAQUS得到動力擾動后圍巖應力場及塑性區，并且提出了多種工況下的支護優化方案。劉新穎等[5]對高滲透壓下圍巖穩定性進行分析，得到了圍巖開挖后應力場以及位移場分布特征和開挖卸載對滲流場的影響。董春亮等[6]研究了深部圓形巷道開挖卸荷的圍巖力學特征及破壞機理。得到開挖卸荷下的圍巖應力場特征為為最小主應力卸荷、最大主應力集中，而主應力差的瞬間增大，從而使得圍巖裂隙擴展，形成連續分布的破壞區。傳統塑性力學在圍巖應力與變形的求解過程中，將引入Mohr-Coulomb或Hoek- Brown等屈服準則[7?11]。然而，屈服準則的選用不同，得到的應力場結果也將出現差異，這種不確定性將導致圍巖應力場與實際情況不相符[12?14]。彈塑性折線理論可以避開屈服準則的影響，確定兩類邊界條件下彈塑性問題的準確應力場，取得了如下重大成果：當邊界條件全為應力邊界條件，或有位移邊界條件但在塑性區邊界上僅有零位移邊界條件(對應力邊界條件沒限制)時，塑性力學問題的應力場表達式完全等同于把所討論問題當成彈性問題求解所獲得的應力場表達式[15?17]，這為隧道開挖進入彈塑性狀態后圍巖的擾動分析奠定了理論基礎。李鈾等[14]應用彈塑性折線理論所得應力場新成果對圓形巷道的擾動區和圍巖的臨界破壞深度進行了研究，分析表明擾動區半徑與外載的大小與作用形式、泊松比和埋深有關，有時會遠遠超出隧道最大直線尺寸的3~5倍。本文首先將以彈性力學為基礎，先利用已有的未考慮自重影響的圓形隧道解析解進一步分析擾動區范圍，確定擾動區影響因素，并采用ANSYS得到考慮自重的開挖擾動后圍巖應力場，通過分析得到擾動區大小。然后應用彈塑性折線理論將彈性狀態所得的成果推廣至彈塑性狀態，研究成果將為隧道開挖數值模擬以及支護設計提供依據。

2 彈性狀態圓形隧道擾動區及影響因素分析

如圖1圓形隧道受力模型所示，以隧道中心為原點建立坐標系，水平方向為軸(極坐標系下與極軸重合)，鉛垂方向為軸，隧道軸向為軸，其中為擾動區半徑與軸的夾角(順時針為正，下文簡稱為夾角)，為圓形隧道半徑。

圖1 圓形隧道的受力模型

假設地層各向同性且均質，彈性力學已經求得半空間體在自重應力下的應力場[18]，即隧道開挖之前的原巖應力場：

式中：，，分別為地層深度、容重與泊松比。

設隧道開挖的深度為，隧道半徑為，此時隧道處于平面應變狀態，受力模型如圖1所示。由式(1)的解答，可將和近似表示為：

由擾動區定義易知，擾動區范圍實質上是應力變化大于5%的區域，因此通過轉換使得開挖前后應力處于相同坐標系下，再來研究擾動區范圍更為方便。因此先將文獻[18]所得圖1模型極坐標系下的解答，轉換成平面直角坐標系下的解答：

式中：為水平應力；為鉛垂應力；為剪應力。

現研究水平應力與鉛錘應力來確定擾動區半徑，根據定義擾動區半徑為

式中：表示擾動后圍巖應力；表示原巖應力。

因此對式(3)有：

式中：r為水平應力擾動區半徑；r為鉛垂應力擾動區半徑；為r，r與軸之間的夾角。

由式(4)~(6)可得到r和r與泊松比、夾角及隧道半徑之間的關系，示于圖2，圖2中=2 m。

圖2 r~θ曲線(a=2 m)

由圖2可得擾動區的如下特點：

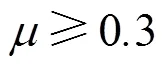
0°方向水平應力：

90°方向水平應力：

90°方向鉛垂應力：

式(7)~(9)中泊松比為0.1~0.4。式(7)~(9)即可確定擾動區半徑的最大值。

上述分析表明，圓形隧道擾動區范圍可能超出“井巷或采場最大直線尺寸的3~5倍”這個范圍。因此在確定擾動區范圍以及數值模型的計算域時應根據具體情況(泊松比、隧道半徑、夾角)而定，不然將對圍巖應力場和隧道的支護設計產生影響。

2 考慮自重的圓形隧道數值結果及分析

自重對圍巖的變形與應力分布有重要影響，上面分析未涉及自重的影響，下面進一步研究自重對圓形隧道擾動區的影響。因考慮自重時，難以獲得解析解，下面利用ANSYS數值方法進行研究，計算參數如表1所示。

假設地層是均質且各向同性，開挖擾動后，圍巖處于彈性狀態。建立彈性狀態數值模型如圖4所示，為盡可能減小尺寸效應，取較大的數值模型尺寸，為長×寬=120 m×120 m，以圓形隧道圓心為原點建立坐標系，軸即水平軸，軸為鉛垂軸，隧道軸線方向為軸。隧道模型上邊界采用應力邊界，施加均布荷載=(?60)，為隧道圓心埋深。模型左右邊界限制水平位移，下邊界限制豎向位移，有限元網格見圖4。

表1 數值模型計算參數

圖4 圓形隧道有限元網格

2.1 有無自重情況下應力場對比分析

圖5給出了0°和90°方向最大與最小主應力的分布情況，作為對比，圖中也給出了不考慮自重時的計算結果，結果表明：不考慮自重將導致所得主應力數值偏小，這樣，應用摩爾?庫倫準則來判斷圍巖的臨界破壞區域時，計算結果較不安全，將直接影響到支護設計結果。

2.2 考慮自重情況下擾動區半徑分析

考慮自重時擾動區半徑如圖6所示，從圖6 可知：

1) 相對來說，隧道開挖對的影響較小，由確定的擾動區范圍均處于隧道最大直線尺寸的5倍以內。

2) 鉛垂應力、軸向應力、水平應力共同確定的最大擾動區半徑與由主應力確定的最大擾動區半徑均在0°與90°方向上，最大擾動區半徑為12.5 m，為隧道最大直線尺寸的6.25倍。當泊松比為0.25時，本文第2節中采用式(7)~(9)得到擾動區半徑最大值為隧道半徑的6.29倍，兩者結果相近，這表明單純確定擾動區范圍時，第2節中為簡化分析過程，采用水平應力與鉛垂應力來確定擾動區范圍的可行性。

圖5 數值計算域內自重對主應力的影響

3) 在?90°，?45°，0°， 45°，90°方向上，確定的擾動區范圍均超過隧道最大直線尺寸的5倍，其它各個方向上為隧道最大直線尺寸的3~5倍以內。

4) 在?90°，?75°，75°，90°方向上，確定的擾動區范圍較大，其中90°方向上擾動范圍最大，其擾動區半徑為12.5 m，為隧道最大直線尺寸的6.25倍；75°方向上擾動區半徑為10.88 m，為隧道最大直線尺寸的5.44倍。其他方向上擾動區范圍大致為隧道最大直線尺寸的5倍以內。

5) 如圖6(b)所示，應該注意的是，在0°和90°方向上，第2主應力擾動區半徑均為12.5 m，為隧道最大直線尺寸的6.25倍。這也表明，隧道開挖對第2主應力的影響也是不容忽視的。

通過上面的分析并與不考慮自重的情況對比，可以看出不考慮自重與考慮自重情況對擾動區范圍影響不大。

圖6 擾動區半徑(a=2 m)

2.3 泊松比、洞徑與隧道埋深變化對擾動區范圍的影響

2.3.1 泊松比變化對擾動區范圍的影響

仍采用圖4所示受力模型，研究=0.2，=0.25，=0.3時，擾動區范圍的變化，計算結果如圖7所示。

1) 如圖6(a)所示，泊松比變化對σ確定的擾動區范圍影響較大。①當=0.2，擾動區半徑的最大值在0°方向，擾動區半徑為16.75 m，為隧道最大直線尺寸的8.38倍。在?75°，?30°，30°和75°方向上，擾動區半徑為隧道最大直線尺寸的4~5倍。在其它方向上，擾動區范圍均超過隧道最大直線尺寸的5倍。②當=0.3，在?90°和90°方向上，擾動區范圍分別為11.25 m和11.5 m，分別為隧道最大直線尺寸的5.63倍和5.75倍。在其他方向上，擾動區范圍均在隧道最大直線尺寸的5倍以內。

2) 如圖6(b)和圖6(c)所示，隨著泊松比的變化，和確定的擾動區半徑變化并不明顯。①確定的擾動區半徑的最大值在?90°與90°方向上，大致為隧道最大直線尺寸的6.1倍②確定的擾動區半徑均在隧道最大直線尺寸的5倍以內。

3) 由式(7)，式(8)和式(9)可得，當泊松比為0.2，0.25和0.3時，圖1模型利用彈性力學解析解確定的擾動區范圍的最大值分別為隧道最大直線尺寸的8.29，6.28和6.06倍；本節基于圖4數值模型所得到的最大擾動區范圍分別為隧道最大直線尺寸的8.38，6.25和6.1倍。不同的處理方式，結果基本吻合，這表明了式(7)，式(8)和式(9)在確定擾動區范圍上的簡潔性與適用性。

因為最大擾動區半徑在0°或90°方向上，因此為了簡化分析過程，可以由0°和90°方向上的水平應力與鉛垂應力來確定擾動區范圍。

圖7 泊松比變化對擾動區范圍的影響

2.3.2 洞徑變化對擾動區范圍的影響

取隧道半徑為1，1.5和2 m進行計算，計算模型同圖4，計算參數同表1，結果如表2所示。

表2示出了隨著隧道半徑的增大，最大擾動區半徑線性增大，數值解與解析解求得的最大擾動半徑相近，且在泊松比確定的情況下，最大擾動區半徑與隧道半徑的比值是常數，這與第2節中式(7)，式(8)和式(9)所得成果是相同的。因此本節中基于隧道半徑為2 m所得到的擾動區結果同樣適用于其他洞徑情況。

表2 最大擾動區半徑與隧道半徑關系

2.3.3 隧道埋深變化對最大主應力及擾動區范圍的影響

取分別為300，500和900 m 3種情況進行計算，計算參數同表1，洞壁上最大主應力隨夾角的變化如圖8所示，可知：洞壁處最大主應力在0°方向上有最大值，隨著隧道埋深增加，最大主應力不斷增大。下面給出0°方向上洞壁處最大主應力隨隧道埋深變化，如圖9所示。

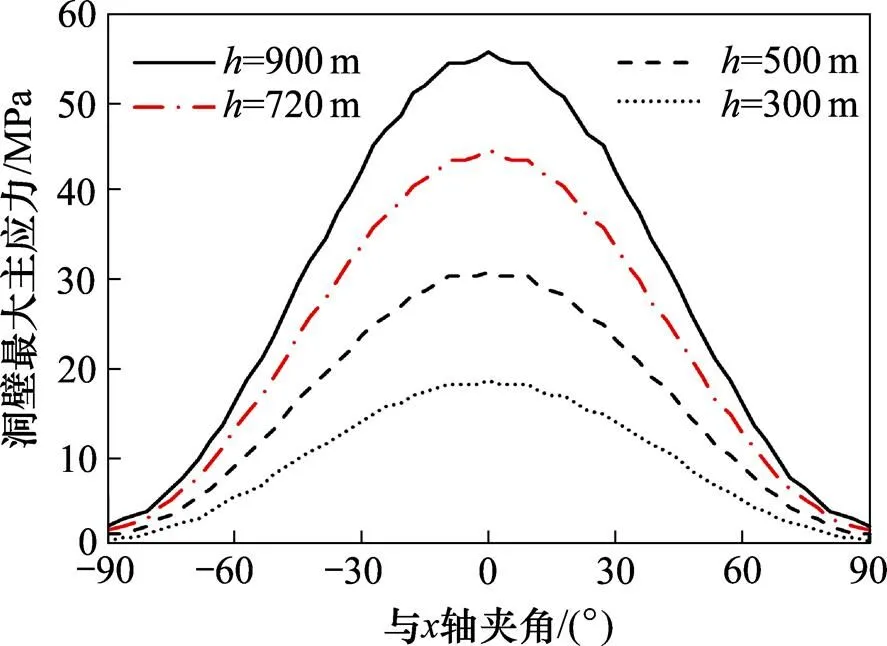
圖8 洞壁最大主應力與夾角關系(μ=0.25)

圖9 0°方向洞壁最大主應力隨隧道埋深變化規律

結果表明，隨著隧道埋深的增加，最大主應力線性增加。盡管隧道周圍應力的大小上出現變化，但是其他隧道埋深情況下應力分布規律與隧道埋深為720 m相似。經分析，前文基于隧道埋深為720 m得到的擾動區范圍研究成果同樣適用其他隧道埋深情況。

3 其他截面形式圍巖擾動區分析

其他截面形式的隧道開挖，因難以獲得圍巖應力場解析解，下面以隧道中心為坐標原點建立ANSYS數值模型，分析矩形與直墻半圓拱截面形式圍巖擾動區大小，它們有相同的高度與跨度，隧道尺寸如圖(10)所示，地層參數同表1，數值計算模型邊界尺寸及邊界條件同第3節。

如圖10模型，得到隧道洞壁?90°~90°方向上最大主應力與最小主應力，結果如圖11所示。

圖10 矩形與直墻半圓拱截面

圖11 2種截面形式主應力對比

對于圖10的2種截面而言，最大主應力與最小主應力峰值?45°方向附近，這與底板與側墻相交處應力集中有關。直墻半圓拱形式的最大拉應力出現在底板中部，矩形截面形式最大拉應力值在底板與頂板中部，由于巖石抗拉強度較差，當隧道埋深較深時，底板與頂板中部巖石將以拉伸破壞的形式出現。

研究矩形與直墻半圓拱2種截面形式最大擾動區范圍，研究方法同第3節，結果如圖12所示。

對于圖10模型而言，2種截面形式擾動區半徑在?90°和90°方向上有峰值。其中，矩形截面形式最大擾動區半徑在90°方向上有最大值，最大擾動區半徑為15.38 m，為隧道最大直線尺寸的5.78倍；直墻半圓拱截面形式，在?90°方向上擾動區半徑有最大值，擾動區半徑為14.63 m，為隧道最大直線尺寸的6.27倍，最大擾動區半徑均超過隧道最大直線尺寸的5倍。

圖12 3種截面形式擾動區半徑

由圖12可知，相同高度與跨度情況下，矩形截面的最大擾動區半徑最大，圓形截面的最大擾動區半徑最小。因此從減小擾動區的范圍角度講，采用圓形截面要比直墻半圓拱與矩形截面更好。

4 彈塑性狀態圍巖擾動區分析

當隧道開挖進入深部時或地應力較大時，隧道圍巖的應力場將進入彈塑性狀態，若圍巖彈塑性應力場的確定出現較大誤差，由此得到的擾動區范圍就會出現較大偏差。傳統彈塑性理論采用了尚在研究的不準確的屈服準則或加載準則，這就會導致彈塑性應力場的不準確。彈塑性折線理論可以避開屈服準則或加載準則的影響，因此可以得到隧道圍巖開挖擾動后彈塑性狀態圍巖準確應力場。

假設圍巖處于小變形狀態，圖1與圖4受力模型的邊界條件將滿足彈塑性折線理論的重要成果的2類邊界條件[15?16]，此時，彈塑性力學問題的應力場表達式完全等同于把所討論問題當成彈性問題求解所獲得的應力場表達式。所以，即使圍巖進入塑性狀態，上文中的應力場解答也是準確的。因此上文中彈性狀態圍巖擾動分析所得到的成果將同樣適用于彈塑性狀態圍巖擾動分析。

5 結論

1) 隧道擾動區的影響因素有隧道截面與尺寸、泊松比等。

2) 總結出了圓形隧道0°與90°方向上水平應力與鉛垂應力擾動區半徑與泊松比、隧道半徑的多項式關系。

3) 圓形、直墻半圓拱、矩形3種截面形式的最大擾動區范圍均超出了隧道截面最大直線尺寸的5倍，即一般情況下大于現時認為的3~5倍。因此數值計算模型的尺寸應根據擾動區的大小適當擴大。

4) 從減小擾動區范圍的角度出發，相同高度與跨度的圓形、直墻半圓拱、矩形3種隧道截面對比，圓形截面最優，直墻半圓拱截面次之，矩形截面 最差。

[1] 高磊. 礦山巖體力學[M]. 北京: 冶金工業出版社, 1979: 83?84. GAO Lei. Mine rock mechanics[M]. Beijing: Metallurgy Industry Press, 1979: 83?84.

[2] 周輝, 渠成堃, 王竹春, 等. 深井巷道掘進圍巖演化特征模擬與擾動應力場分析[J]. 巖石力學與工程學報, 2017, 3(8): 1821?1831. ZHOU Hui, QU Chengkun, WANG Zhuchun, et al. Simulating the variation of surrounding rock and analyzing the disturbed stress field during excavation of deep mine roadway[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(8): 1821?1831.

[3] 趙維生, 韓立軍, 張益東. 垂直交岔點擾動主應力變化規律及圍巖穩定性研究[J]. 采礦與安全工程學報, 2015, 32(1): 90?98. ZHAO Weisheng, HAN Lijun, ZHANG Yidong. Variation of disturbance principal stress and stability of surrounding rock at vertical intersection[J]. Journal of Mining and Safety Engineering, 2015, 32(1): 90?98.

[4] 唐禮忠, 陳源, 鄧麗凡, 等. 擾動下含接觸帶巷道圍巖力學響應及控制研究[J]. 鐵道科學與工程學報, 2016, 13(2): 309?315. TANG Lizhong, CHEN Yuan, DENG Lifan, et al. The mechanical response features and control of surrounding rock with contact zone under dynamic disturbance[J]. Journal of Railway Science and Engineering, 2016, 13 (2): 309?315.

[5] 劉新穎, 曹平, 劉濤影, 等. 不襯砌水工隧洞圍巖穩定性數值模擬分析[J]. 鐵道科學與工程學報, 2012, 9(3): 45?50. LIU Xinying, CAO Ping, LIU Taoying, et al. Numerical simulation analysis of surrounding rock stability of unlined high pressure hydraulic tunnels[J]. Journal of Railway Science and Engineering, 2012, 9(3): 45?50.

[6] 董春亮, 趙光明, 李英明, 等. 深部圓形巷道開挖卸荷的圍巖力學特征及破壞機理[J]. 采礦與安全工程學報, 2017, 34(3): 511?518. DONG Chunliang, ZHAO Guangming, LI Yingming, et al. Mechanical characteristics and failure mechanism of surrounding rock of deep circular roadway excavation unloading[J]. Journal of Mining and Safety Engineering, 2017, 34(3): 511?518.

[7] LONG L, KANG H, MO R. Three-dimensional plastic stress analysis of subsea tunnels: Nonlinear vs. linear-a comparison[J]. Ksce Journal of Civil Engineering, 2017, 21(1): 178?183.

[8] Zareifard M R, Fahimifar A. Effect of seepage forces on circular openings excavated in Hoek–Brown rock mass based on a generalised effective stress principle[J]. European Journal of Environmental and Civil Engineering, 2014, 18(5): 584?600.

[9] Sharan S K. Exact and approximate solutions for displacements around circular openings in elastic-brittle- plastic Hoek-Brown rock[J]. International Journal of Rock Mechanics & Mining Sciences, 2005, 42(4): 542?549.

[10] Russo Bello F, Murphy S K. Long walling at great depth in a geologically disturbed environment. The way forward[J]. The Journal of South African Institute of Mining and Metallurgy, 2000, 100(2): 91?100.

[11] Sharan S K. Analytical solutions for stresses and displacements around a circular opening in a generalized Hoek-Brown rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45(1): 78?85.

[12] 李鈾, 彭意. 論圓形斷面井巷圍巖彈塑性應力莫爾?庫倫準則解答[J]. 土工基礎, 2006, 20(2): 71?72. LI You, PENG Yi. Discussion on elastic-plastic stress solution of circular section surrounding rock based on Mohr-Coulomb criterion[J]. Soil Engineering and Foundation, 2006, 20(2): 71?72.

[13] 李鈾, 袁亮, 劉冠學, 等. 深部開采圓形巷道圍巖破損區與支護壓力的確定[J]. 巖土力學, 2014, 35(1): 226?231. LI You, YUAN Liang, LIU Guanxue, et al. Determination of failure zone and support pressure of circular roadway under deep mining[J]. Rock and Soil Mechanics, 2014, 35(1): 226?231.

[14] 李鈾, 袁亮, 劉冠學, 等. 圓形巷道圍巖擾動區及其臨界破壞深度的確定[J]. 采礦與安全工程學報, 2016, 33(5): 795?799. LI You, YUAN Liang, LIU Guanxue, et al. Determination of disturbed region and critical failure depth of surrounding rock in circular roadway.[J]. Journal of Mining & Safety Engineering, 2016, 33(5): 795?799.

[15] 李鈾. 塑性力學問題的一種求解新方法及應用[D]. 武漢: 中國科學院武漢巖土力學研究所, 2002. LI You. A new method of plasticity theory and Its application[D]. Wuhan: Wuhan Institute of Geotechnical Mechanics, Chinese Academy of Sciences, 2002.

[16] 李鈾. 塑性力學引論[M]. 2版. 北京: 科學出版社, 2018. LI You. Introduction to plastic mechanics[M]. 2nd ed. Beijing: Science Press, 2018.

[17] LI Y. New research on the stress field of elastic–plastic small deformation problems[J]. Journal of Materials Processing Tech, 2003, 138(1): 508?512.

[18] 徐芝綸. 彈性力學(上冊)[M]. 北京: 人民教育出版社, 1979: 267?269.XU Zhilun. Elastic mechanics (Volume 1)[M]. Beijing: People’s Education Press, 1979: 267?269.

Analysis of stress disturbed zone of tunnel and its influence factors

HE Xun, LI You

(School of Civil Engineering, Central South University, Changsha 410075, China)

The range of the disturbed zone is generally considered to be 3 to 5 times the maximum linear dimension of the tunnel cross section. The existing circular tunnel analytical solution without considering its own weight was used to determine the influence factors of the circular tunnel disturbed zone and the range of the disturbed zone within the elastic state. The polynomial relationship between the radius of the circular tunnel and disturbed zone and the tunnel radius to Poisson’s ratio was obtained. ANSYS was used to analyze the stress field and disturbed zone of the tunnel’s surrounding rocks with circular, straight wall semi-circular arch and rectangular excavation respectively. With applying the new stress field solution from the broken line theory of Elastoplastic mechanics, the results of elastic state analysis were extended to elastic-plastic state. The main results are listed as follows: The maximum disturbed zone of the three different sections (circular, rectangular and straight wall semi-circular arches) all exceeds the maximum linear dimension of the tunnel section by 5 times, which is generally greater than the current 3 to 5 times. Under the same condition of height and span, the circular cross section tunnel was found to be the best to reduce the range of the disturbed zone, followed by straight wall semi-circular arch section tunnel and rectangular section tunnel. In addition, this study provides reference for tunnel support design and the selection of numerical model calculation domain.

circular tunnel; surrounding rocks; stress disturbed zone; numerical simulation; elastoplastic analysis

U453.2

A

1672 ? 7029(2019)11? 2782 ? 09

10.19713/j.cnki.43?1423/u.2019.11.018

2019?02?26

國家自然科學基金資助項目(51874351)；湖南省科技計劃資助項目(2014SK3226)

李鈾(1961?)，男，湖南臨湘人，教授，博士，從事巖石力學與工程、彈塑性力學方面的研究；E?mail：yli@csu.edu.cn

(編輯 蔣學東)