基于點線一致的既有鐵路線路縱斷面自動重構方法
李偉,周雨,王杰,梁家軒,彭先寶,蒲浩
基于點線一致的既有鐵路線路縱斷面自動重構方法
李偉1, 2,周雨1, 2,王杰3,梁家軒1, 2,彭先寶4,蒲浩1, 2
(1. 中南大學 土木工程學院,湖南 長沙 410075;2. 高速鐵路建造技術國家工程實驗室,湖南 長沙 410075;3. 軌道交通工程信息化國家重點實驗室(中鐵一院),陜西 西安 710043;4. 中鐵第四勘察設計院集團有限公司,湖北 武漢 430063)
既有鐵路經過長期運營,縱斷面線形不可避免偏離原設計線位,必須定期重構出調整量最小且滿足約束的線位,以保證列車安全運行。縱斷面線形由一系列直線和豎曲線線元順次光滑連接而成,重構關鍵在于準確識別每個測點歸屬的線元,并顧及約束進行擬合。本文提出測點歸屬應與重構線元完全相符的“點線一致”思想,據此構建縱斷面自動重構方法。根據二階差商初步完成測點歸屬識別,分別擬合對應線元,根據線元范圍反向調整測點歸屬,迭代上述過程直至點線一致,并在迭代中處理各類約束。基于該方法研發的軟件已在兩千多公里既有線縱斷面重構中應用,實例表明該方法可準確識別測點歸屬,自動生成滿足約束、抬落道量顯著優于既有方法的重構線形。
既有鐵路;線路縱斷面;點線一致;自動重構

既有鐵路在長期的運營中,由于輪軌相互作用、基礎變形等因素導致縱斷面線形不同程度地偏離原設計線位。為保障運營安全,必須定期對既有線的軌面標高進行測量,并重構出平順的縱斷面線形,否則軌道變形累積,沖擊作用惡性循環,危及行車安全,甚至引發脫軌[1]。為減少對運營的干擾,既有線縱斷面重構并非簡單地將變形后的縱斷面軌面調整到原設計線位,而是對既有的軌面測量點進行擬合,得到一條抬落道量最小,且滿足多種約束的縱斷面重構線形。縱斷面線形由一系列直線和豎曲線線元順次光滑連接而成。由于直線、豎曲線的回歸方程不同,因此需識別出各測點歸屬的線元,然后顧及各類約束分別擬合對應線元。國內外學者針對線路縱斷面重構已開展大量研究,總體來說,歷經3個階段: 1)人工識別:以測點里程為橫坐標,曲率、切線角、正矢等為縱坐標,生成各類線形特征圖,從圖中人工識別各測點歸屬的線元,再進行線元擬合。該類方法十分耗時,依賴設計人員的經驗,識別準確度不高,重構出的線路抬落道量偏大。2)迭代識別:為克服人工識別的不足,孟凡超等[2?3]提出測點歸屬識別的迭代方法。該方法以人工識別分段結果為初值,以線元分界點位置穩定為收斂條件,構造迭代過程[4]。該類方法提升了測點歸屬識別的準確度,重構線形的抬落道量優于人工識別。但此類方法仍然需要人工參與,無法自動重構,未考慮容許抬落道量等約束。3)整體優化:近年來大量學者將縱斷面重構視為最優化問題,以變坡點位置及豎曲線半徑為自變量,抬落道量平方和為目標函數,建立優化模型,采用遺傳算法[5]、廣義簡約梯度技術(GRG)等,借助數學軟件[6]求解。此類方法進一步提升縱斷面線形重構效果,但仍需借助前兩類方法產生初值。若初值不準確,如變坡點個數識別錯誤,將難以產生優化的重構結果。而且此類方法同樣缺少對線形約束的有效處理。除了縱斷面重構,國內外學者對平面重構也開展了大量研究,先后提出方向加速法[7]、啟發式算法[8]、振蕩迭代[9]等一系列方法。但相比平面,縱斷面直線線元間的轉角較小,豎曲線半徑較大、約束不同,平面線形重構方法并不完全適用于縱斷面[10]。綜上,國內外學者針對既有線的平縱面線形重構都開展了大量卓有成效的研究,但既有的平面重構方法難以適用于縱斷面線形[11?12]。既有縱斷面重構方法具有以下不足之處:1)測點歸屬識別精度尚待提升; 2)需人工輔助,非自動重構;3)對縱斷面線形的約束處理不足。針對上述問題,本文提出基于點線一致的縱斷面重構算法。該方法可以實現縱斷面的全線自動精準重構,并處理縱斷面重構中的各類約束。
1 “點線一致”縱斷面線形重構思想
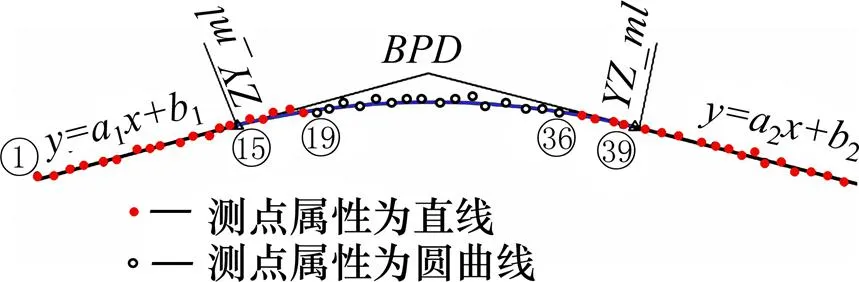
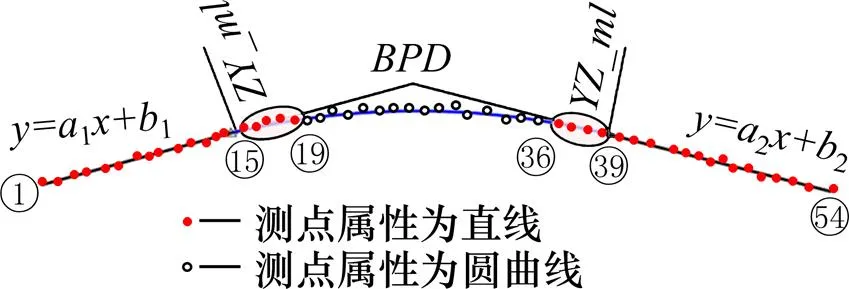
線路縱斷面中直線和豎曲線線元并非獨立存在,必須滿足相鄰線元首尾相接且相切的光順性條件。如果依據識別的測點歸屬,單獨擬合各直線和豎曲線線元,生成的縱斷面線形無法滿足光順性條件(如圖1)。而在考慮光順性條件后,則可能出現識別的測點歸屬與最終擬合出的線元范圍不一致(如圖2),此時的線元擬合并非最優。既有的重構方法中往往將測點識別與線元擬合作為兩個獨立過程,忽略光順連接問題。

圖1 直曲連接處不平順
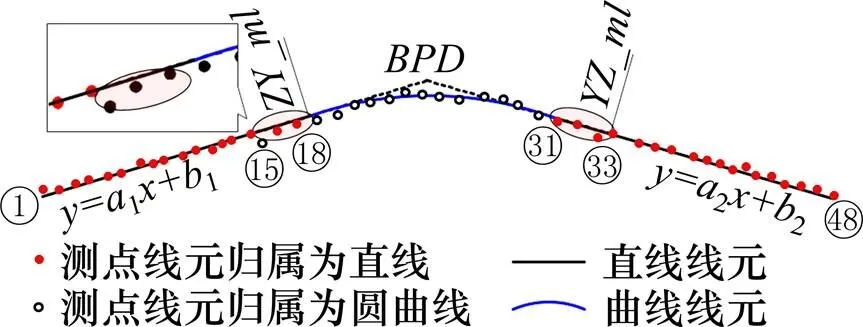
圖2 測點線元歸屬不一致
對此,本文提出縱斷面線形重構中的“點線一致”思想:對于每一組歸屬于直線或豎曲線的測點群,考慮光順性進行擬合后,形成的線元剛好完全包含對應點群,此時稱為“點線一致”。如果所有測點與線元均達到點線一致,則所有線元為最優擬合,測點到重構后線形調整量最小。本文不再將測點識別與線元擬合作為2個獨立過程,而是基于“點線一致”思想,提出一種測點歸屬識別與線元擬合交錯執行的循環迭代方法,其基本流程如下:
1) 基于二階差商進行測點歸屬的初步識別;
2) 依據各測點歸屬,并顧及各類約束條件,分別擬合出直線、豎曲線線元;
3)檢測擬合后的線元范圍與測點歸屬是否達到點線一致;
4)若實現點線一致,終止迭代,得到縱斷面重構線形;否則依據線元范圍反向調整各測點歸屬,轉第2步,繼續迭代上述過程直到點線一致。
2 基于二階差商的測點歸屬初步識別
既有鐵路縱斷面線形中,直線坡段與豎曲線坡段的坡度變化率有顯著區別。采用既有軌面各測點的里程X和高程Y數據計算坡度變化率,可初步判斷測點屬性。坡度變化率為高程關于里程的二階導數。但=()為離散函數,不可導,故采用二階差商[13]計算二階導數近似值:
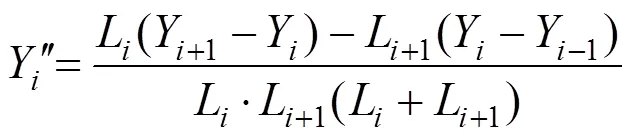
其中:
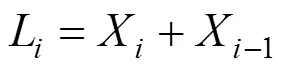


圖3 既有線縱斷面測點二階差商
3 線元擬合
3.1 基于穩健最小二乘直線坡段擬合
3.1.1 穩健最小二乘擬合直線線元
測點初步分段后,首先將線元歸屬為直線的測點,以抬落道量平方和最小為目標,根據最小二乘原理進行直線擬合。但高程數據的粗差或異常值對擬合坡度值影響較大,解算時,應對粗差或異常值予以剔除[14],以獲取穩健的直線參數最佳估值。具體解算步驟如下:
設直線坡段對應測點個數為,軌面測點數據為(x,y),直線坡段方程,坡段抬落道量平方和為:
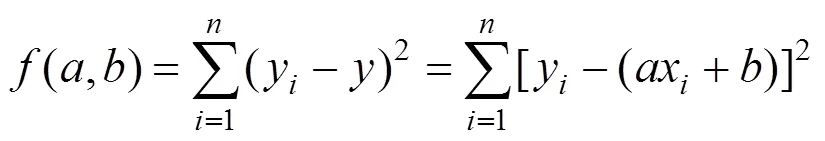
1)()分別對,求一階偏導為0時,可解得抬落道量平方和最小時初始值0,0:

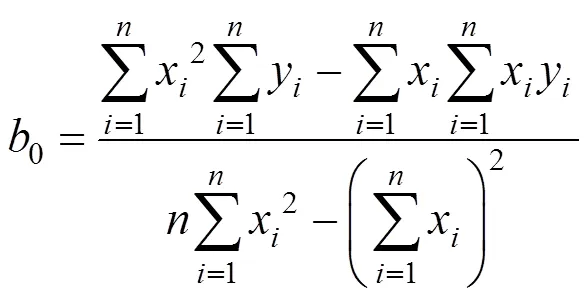
2)根據初始值0,0,計算每個測點至擬合直線的距離:

3)計算測點至直線的距離d的標準差:
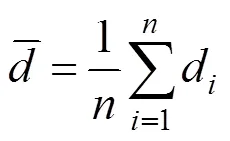
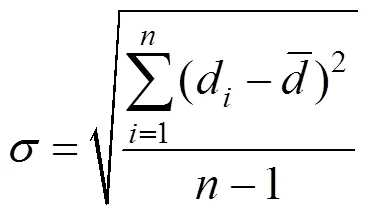
4)遍歷測點,根據3原則,若d≤3,將測點保留,否則為異常點,須剔除;
5)余下測點重新進行最小二乘擬合,重復步驟1~4,直至所有測點均滿足d≤3為止;
6)利用余下測點進行穩健最小二乘擬合,獲取,最可靠值;
3.1.2 坡段求交
相鄰2直線坡段方程聯立求解變坡點坐標(X,Y):

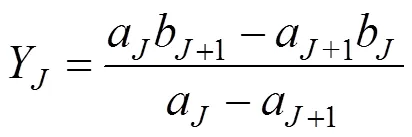
當出現下列情況時,須將相鄰坡段合并,再次擬合求交:


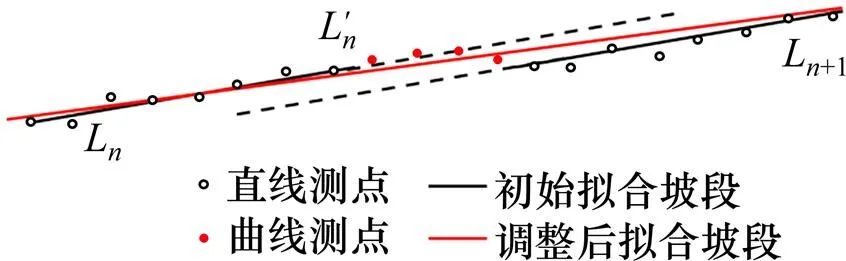
圖4 相鄰擬合坡段平行

圖5 變坡點未在豎曲線測點范圍內
3.1.3 約束處理
縱斷面直線坡段重構還存在最大坡度、容許抬落道量、最小坡長等約束。各類約束處理方法如下:
1) 最大坡度
直線坡段的方程為,其中即為坡度,需小于最大容許上行坡度imax,大于最大容許下行坡度?imax即
?imax≤≤imax(11)
2)最小坡長
①坡長接近且小于最小坡長min的坡段,向坡長較大的相鄰坡段方向微調,如圖6;
②坡長小于最小坡長min的坡段,與坡長較小的相鄰坡段合并,如圖7。

圖6 變坡點微調示意圖
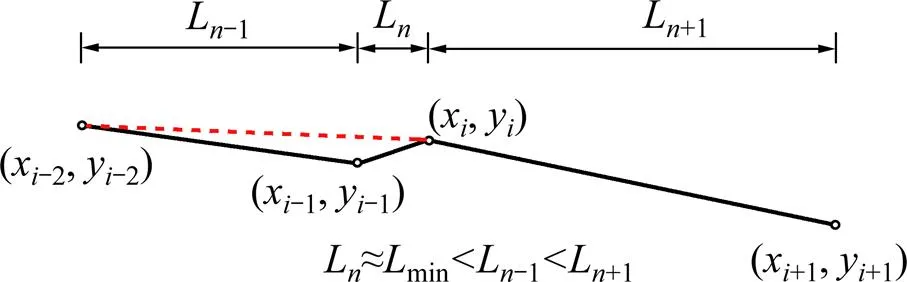
圖7 相鄰坡段合并示意圖
3) 容許抬落道量
重構線路時,鐵路縱斷面存在一系列必須滿足的抬落道要求,包括:
①橋梁段:不允許落道,以避免降低墩臺頂面高,導致施工困難。抬道量控制在10~15cm范圍,以避免道砟加厚對橋梁應力及穩定性的不利影響:
0.0≤ax+b?y≤0.15 (12)
②隧道段:一般采用落道以避免列車侵 限[15],落道量應控制在0.4m以內,以保護隧道邊墻基礎[15]:
?0.4≤ax+b?y≤0.0 (13)
③有支擋構造物路基段:避免因路基加寬時,填土坡腳蓋過擋土墻或護坡。根據該條件反算出最大容許抬道量Tmax,則有:
ax+b?y≤Tmax(14)
④施工方法受限路段:對于不能采用抬降路基面的施工方式進行軌道調整的路段,其抬道量應小于100cm,落道量需滿足最小道床厚度的要求。根據實測道床厚,可反算出容許落道量Lmax,則有:
?Lmax≤ax+b?y≤1.0 (15)
⑤運營條件約束:為減輕對運營干擾,盡量避免挖切路基或道床來降低軌面高程,因此,既有軌道盡量不進行落道。
綜上,各測點須滿足橋梁、隧道等特殊路段及施工方法、運營條件等多方面對抬落道量的約束,保證抬落道量在容許最大落道量?max和容許最大抬道量max之間:
?max≤ax+b?y≤max(16)
聯立式(3),(11)和(16),可得出顧及最大坡度、特殊路段控制抬落道量等約束的直線坡段擬合 模型:

這是線性約束下的二元二次最優化問題,可以采用增廣拉格朗日法或者序列二次規劃法 求解[16]。
為提高計算效率,在實際使用過程中,可先按無約束的最小二乘擬合直線坡段。如果生成的直線滿足所有約束則可直接使用,否則求解約束最優化問題。
3.2 豎曲線擬合
豎曲線部分須實現抬落道量平方和最小,同時須滿足與相鄰兩直線線元相切的光順性條件以及容許抬落道量、豎曲線與緩和曲線(道岔)不重疊等約束。
3.2.1 目標函數
假設豎曲線坡段測點(x,y);豎曲線半徑為;前后兩坡段轉角為;目標函數為豎曲線范圍的測點抬落道量平方和,可表示為:
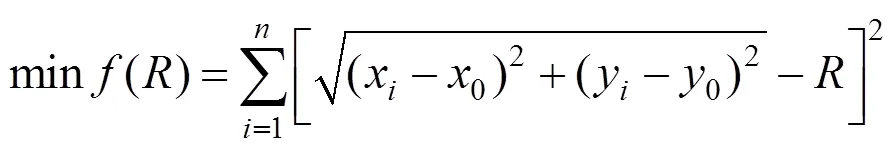
3.2.2 約束條件
1) 光順性約束
在縱斷面變坡點處,為保證行車的安全平順,豎曲線應該與相鄰直線坡段相切,如圖8 所示。
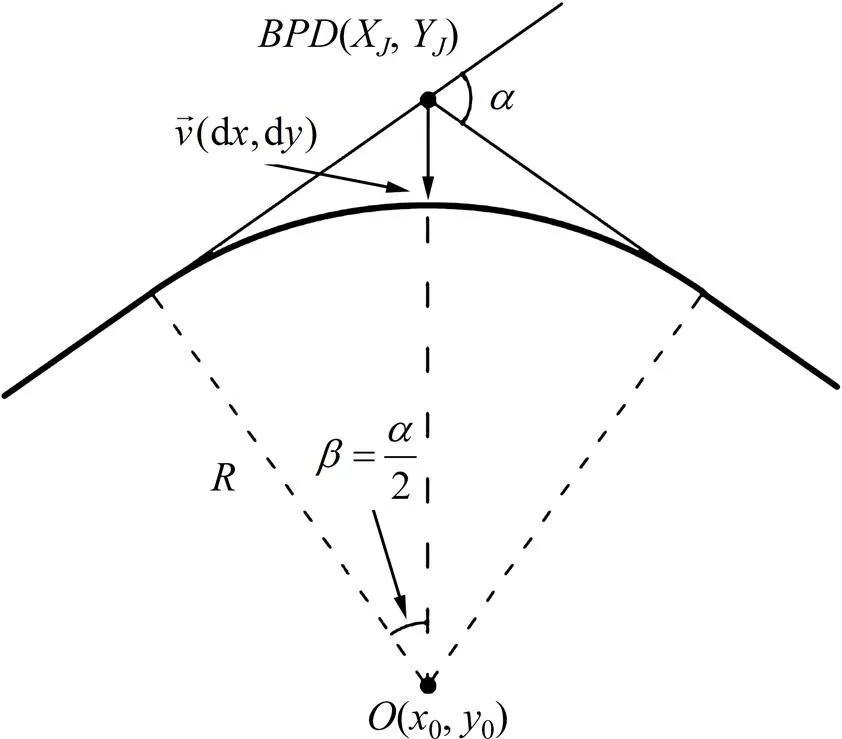
圖8 豎曲線與相鄰直線線元光順連接
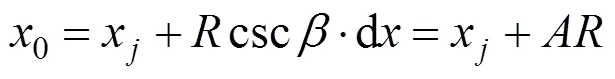
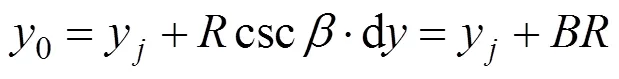
目標函數可表示為:
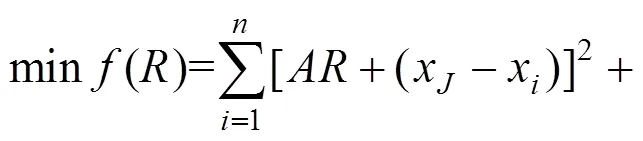
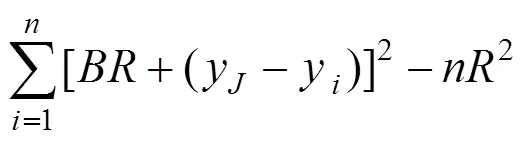
豎曲線段抬落道量平方和是關于的二次函數,當目標函數最小時,′()0,求出半徑:
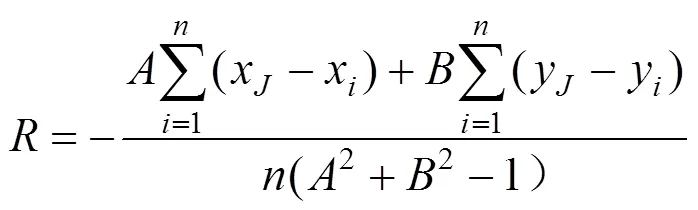
2)抬落道約束
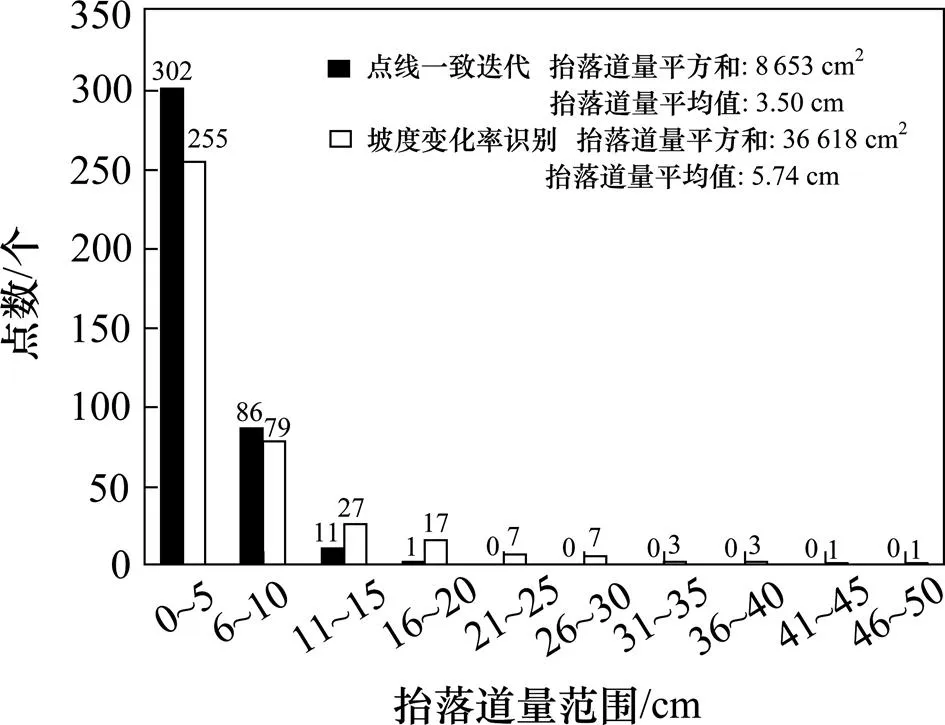
與直線坡段一樣,豎曲線段的抬落道量也應滿足橋梁、隧道、支擋構造物路基、施工方法及運營條件的限制,須在最大落道量?max和最大抬道量max范圍之間:?max 否則,線形須要微調至滿足抬落道約束,具體方法如下: 設豎曲線圓心坐標為(0,0),滿足抬落道量平方和最小的豎曲線初始方程為: 變坡點為J(XJ,YJ),容許抬落道量為?max,相鄰坡段坡度差為α,作?PFO為直角三角形(如 圖9)。 令a=FP=x?0,b=FJ=Y?y0;滿足以下幾何關系: 即: 滿足關系式: 求解得: 其中: 抬道時maxmax,落道時maxmax。滿足容許抬落道約束的取值范圍為: (max)<<(max) 若初始擬合豎曲線抬落道超限,為滿足擬合目標最小及容許抬落道約束,抬道時,調整取值為(max),落道時,將調整取值為(max)。 3)平縱組合約束 縱坡豎曲線部分應避免與平面緩和曲線或道岔重疊。初步確定后,計算豎曲線坡段范圍(,)。若豎曲線與平面緩和曲線、道岔區重疊,須進行以下調整: ①逐步縮小,減小豎曲線范圍,避免 重疊; ②若取規范半徑最小值min時仍重疊,調整變坡點位置,將變坡點向重疊區域減少的方向移動,直至重疊消失; ③若變坡點移動至坡長小于規范min時仍重疊,則刪除該變坡點,重新擬合求交。 為實現線形精準識別重構,完成上述測點歸屬初步識別和線元擬合步驟后,須檢測各線元范圍與識別的測點歸屬是否保持一致。如不一致,則通過交錯迭代執行測點歸屬調整與線元擬合過程,最終達到點線一致。具體算法步驟如下: 步驟1:測點屬性判斷后,對直線測點進行穩健最小二乘直線擬合,并進行坡段求交,得到坡度及變坡點(X,Y); 步驟2:對豎曲線測點進行擬合,求出豎曲線半徑; 步驟3:根據直線方程及豎曲線半徑,求解特征點里程,如直圓點圓直點,如圖10所示; 步驟4:分別遍歷介于直線、豎曲線坡段范圍內所有測點屬性,如有點線屬性不一致,則調整測點屬性,如圖11所示; 步驟5:根據調整后的測點屬性,重新進行直線、豎曲線坡段擬合,如圖12所示; 步驟6:重復步驟1~5,直至點線一致,得到最優縱斷面線形,如圖13所示。 圖10 坡段擬合求交,計算特征點里程 圖11 調整測點歸屬 圖12 迭代擬合坡段,計算特征點里程 圖13 實現擬合結果的點線一致 基于點線一致的迭代重構思想,筆者編制了既有鐵路縱斷面識別重構計算程序,通過“石門?長沙”、“宜昌東?小溪塔”等大量既有線重構算例,驗證該方法較傳統的坡度變化率識別等方法,在減小抬落道量平方和方面,有顯著提升。 選取石門?長沙線K108+850~K128+850段為例,線路長20km,包含400個既有軌面測點,重構后變坡點共23個。傳統坡度識別重構縱斷面線形抬落道量平方和為36618 cm2,點線一致迭代重構的縱斷面線形抬落道量距離平方和為8653 cm2。 將點線一致迭代重構與傳統坡度變化率識別進行比較,點線一致迭代法重構線形的抬落道量在0~10cm范圍內分布更為集中,分布范圍對比如圖14所示。 圖14 抬落道量結果范圍對比 重構完成后,依次對各坡段進行約束檢測,重構線形滿足縱斷面各種約束,檢測結果如表1所示。 表1 重構線路約束檢查 1)提出了點線一致思想,基于該思想構建的鐵路線路縱斷面重構算法相比于既有方法,可顯著減少測點到重構線路的調整量。 2)針對現有方法考慮縱斷面線形約束較少的問題,處理了最小坡長、容許坡度、豎曲線與緩和曲線(道岔)不重疊、施工方法、運營條件及特殊路段(橋梁、隧道、有支擋構造物路基段)對抬落道量的約束,可直接生成滿足各類約束的縱斷面 線形。 3) 本方法自動化程度高,輸入既有線縱斷面測點里程和高程的原始數據后,可自動輸出滿足各類約束的縱斷面優化線形。 [1] 陳峰. 提速線路精密測量、重構與優化整正研究[D].長沙: 中南大學, 2013. CHEN Feng. Research on precision measurement, reconstruction and optimal adjustment of raising speed railway[D]. Changsha: Central South University,2013. [2] 孟凡超, 劉成龍. 鐵路既有線縱斷面線形分段的優化算法[J]. 鐵道建筑, 2014(6): 146?149. MENG Fanchao, LIU Chenglong. The optimization algorithm for linear segmentation of vertical curve type in existing railway[J]. Railway Construction, 2014(6): 146? 149. [3] 郭良浩, 劉成龍, 宋韜, 等. 鐵路既有線平面和豎面線形精確分段方法研究[J]. 鐵道工程學報, 2014(7): 48? 52. GUO Lianghao, LIU Chenglong, SONG Tao, et al. Research on the new method for accurate linear segmentation of plane and vertical curve type in existing railway[J]. Journal of Railway Engineering Society, 2014(7): 48?52. [4] 陳海軍. 既有線有砟軌道優化線形算法研究及其軟件研制[D]. 成都: 西南交通大學, 2013. CHEN Haijun. Study of algorithm on optimization design of existing railway ballast track and software development[D]. Chengdu: Southwest Jiaotong University, 2013. [5] 孫曉麗. 基于遺傳算法的既有線平面及縱斷面整正優化設計[D]. 長沙: 中南大學, 2010. SUN Xiaoli. Optimization design of plane and vertical section of existing railway based on genetic algorithm [D]. Changsha: Central South University, 2010. [6] Easa S M , Kikuchi S. Generalized method for estimating best-fit vertical alignments for profile data[J]. World Academy of Science, Engineering and Technology, 2009, 33: 693?701. [7] 李偉, 蒲浩, 彭先寶. 基于方向加速法的鐵路既有線平面重構優化算法[J]. 鐵道科學與工程學報, 2009, 6(3): 47?51. LI Wei, PU Hao, PENG Xianbao. Existing railway plane line reconstruction algorithm based on direction acceleration method[J]. Journal of Railway Science and Engineering, 2009, 6(3): 47?51. [8] Camacho-Torregrosa F J. Use of heading direction for recreating the horizontal alignment of an existing road[J]. Computer-Aided Civil and Infrastructure Engineering, 2015, 30(4): 282. [9] LI Wei, PU Hao. A method for automatically recreating the horizontal alignment geometry of existing railways[J]. Computer-aided Civil & Infrastructure Engineering, 2019, 34(1): 71–94. [10] Santiago Higuera de Frutos, María Castro. A method to identify and classify the vertical alignment of existing roads[J]. Computer-aided Civil & Infrastructure Engineering, 2017, 32(11): 952–963. [11] LI Wei, PU Hao, Paul Schonfeld, et al. Methodology for optimizing constrained 3-dimensional railway alignments in mountainous terrain[J].Transportation Research Part C, 2016(68): 549–565. [12] LI Wei, PU Hao, Paul Schonfeld, et al. Mountain railway alignment optimization with bidirectional distance transform and genetic algorithm[J]. Computer-Aided Civil and Infrastructure Engineering, 2017, 32(8) 691? 709. [13] 鐘晶. 既有線改建CAD系統縱斷面開發與研究[J]. 鐵道勘察, 2007(6): 67?70. ZHONG Jing. Development and research on profile of CAD system transformation of existing lines[J]. Railway Investigation and Surveying, 2007(6): 67?70. [14] 官云蘭, 周世健, 張立亭, 等. 穩健整最小二乘直線擬合[J]. 工程勘察, 2012, 40(2): 60?62. GUAN Yunlan, ZHOU Shijian, ZHANG Liting, et al. A robust method for fitting a line to point clouds based on TLS[J]. Geotechnical Investigation&Surveying, 2012, 40(2): 60?62. [15] 易思蓉. 鐵路選線設計[M]. 湖北: 武漢大學出版社, 2014. YI SiRong. Principles of railway location and design[M]. Hubei: Wuhan University Press, 2014. [16] Nocedal J, Wright S J. Numerical optimization[M]. 2nd ed. Springer, 2006. Automatic recreating vertical alignment of existing railway based on points-alignment consistency LI Wei1, 2, ZHOU Yu1, 2, WANG Jie3, LIANG Jiaxuan1, 2, PENG Xianbao1, 2, PU Hao1, 2 (1. School of Civil Engineering, Central South University, Changsha 410075, China;2. National Engineering Laboratory for High Speed Railway Construction, Changsha 410075, China; 3. State key Laboratory of Rail Transit Engineering Information (CFSDI), Xi’an 710043, China;4. China Railway Siyuan Survey & Design Group Co, Ltd, Wuhan 430063, China) After a long period of operation, the vertical alignment of an existing railway inevitably deviates from the originally designed centerline. It is important for calibrating track to ensure safety and comfort. The vertical alignment consists of tangents and curves, which are connected smoothly. The key of recreation is identifying the attribution of each measured point and fitting the geometric elements considering constraints. Based on points-alignment consistency that the attributions of measured points to geometric elements should be consistent with the ranges of recreated geometric elements, a method was proposed to recreate vertical alignment automatically. After the initial identification of the points attribution using second divided difference, the corresponding geometric elements were fitted. Then the attribution of points was adjusted according to the range of geometric elements. These above processes were iterated until the points and geometric elements were consistent, meanwhile, various constraints were considered. A software system developed based on this method has been applied in the recreation of more than 2 000 km of existing railways. Applications demonstrate that this method can identify all geometric elements automatically and generate a recreated alignment while satisfying all the applicable constraints. existing railway; vertical alignment; points-alignment consistency; automatic recreating U212.34 A 1672 ? 7029(2019)11? 2684 ? 08 10.19713/j.cnki.43?1423/u.2019.11.006 2019?02?21 國家自然科學基金資助項目(51608543,51778640);湖南省自然科學基金資助項目(2017JJ3382) 蒲浩(1973?),男,四川南充人,教授,博士,從事鐵路線站數字化設計理論與方法研究;E?mail:haopu@csu.edu.cn (編輯 涂鵬)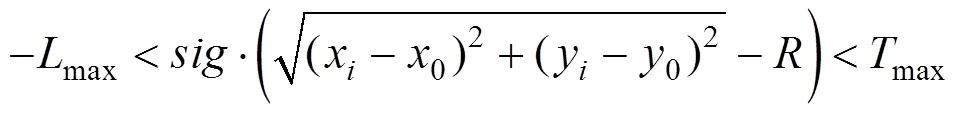

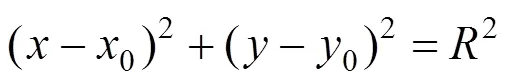


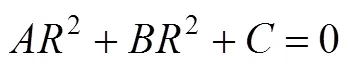

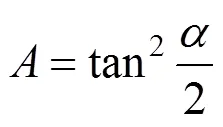
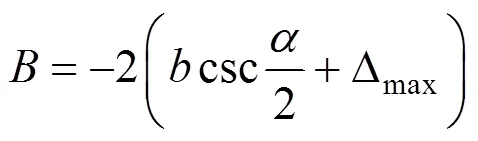

4 基于點線一致的震蕩迭代算法


5 算例分析

6 結論

