線性規劃在水資源優化配置中的應用

曹亞群

(安徽水利水電職業技術學院，安徽 合肥 231603)

隨著社會的不斷發展,水資源出現了短缺,供需矛盾日漸突出,這些問題嚴重制約著社會經濟的可持續發展,為了充分利用有限的水資源,讓水資源最大限度地發揮社會、經濟和環境效益,合理的優化配置水資源、提高水資源利用率是非常必要的。

1 水資源優化配置的原則[1]

所謂水資源優化配置是指在某個地區改善用水量和用水結構,對有限的水資源進行科學合理的分配和利用,其優化配置應遵循的原則如下:

(1)公平性原則。不同區域及社會各階層之間進行水資源的合理分配。不同區域之間需做到協調發展,同一個區域內資源利用效益在社會不同階層中公平分配。

(2)有效性原則。應以水資源的利用效益作為核算經濟成本的重要指標,以生態環境的保護效益作為整個社會健康持續發展的重要指標。為了使水資源能充分被利用,應在水資源優化配置中樹立環境目標、經濟目標及社會發展目標,做到真正實際意義上的有效性。

(3)優先性原則。在各種用水中,優先分配的是生活用水,然后是生態環境用水,最后是生產用水。在保障人民生活、保護好生態環境的前提下加快經濟發展。對于持續干旱時期,應該優先保障人民日常生活用水,同時考慮重點行業用水,然后是保障工業用水,最后是確保農業灌溉用水,在利用水資源時,應首先使用地表水,其次才是地下水。

(4)可持續性原則。它要求當代和后代、近期和遠期在水資源的利用上有一個公平、協調發展,而非掠奪性的開采或破壞,也就是當代人利用水資源,不應該剝奪下一代人享有利用水資源的權利。

2 水資源優化配置屬性[2]

水資源優化配置具有多水源、多要素、多用戶及多目標的屬性,同時具有一定的層次性與關聯性,如圖1所示。統籌考慮不同屬性的重要程度,是水資源優化配置的前提。

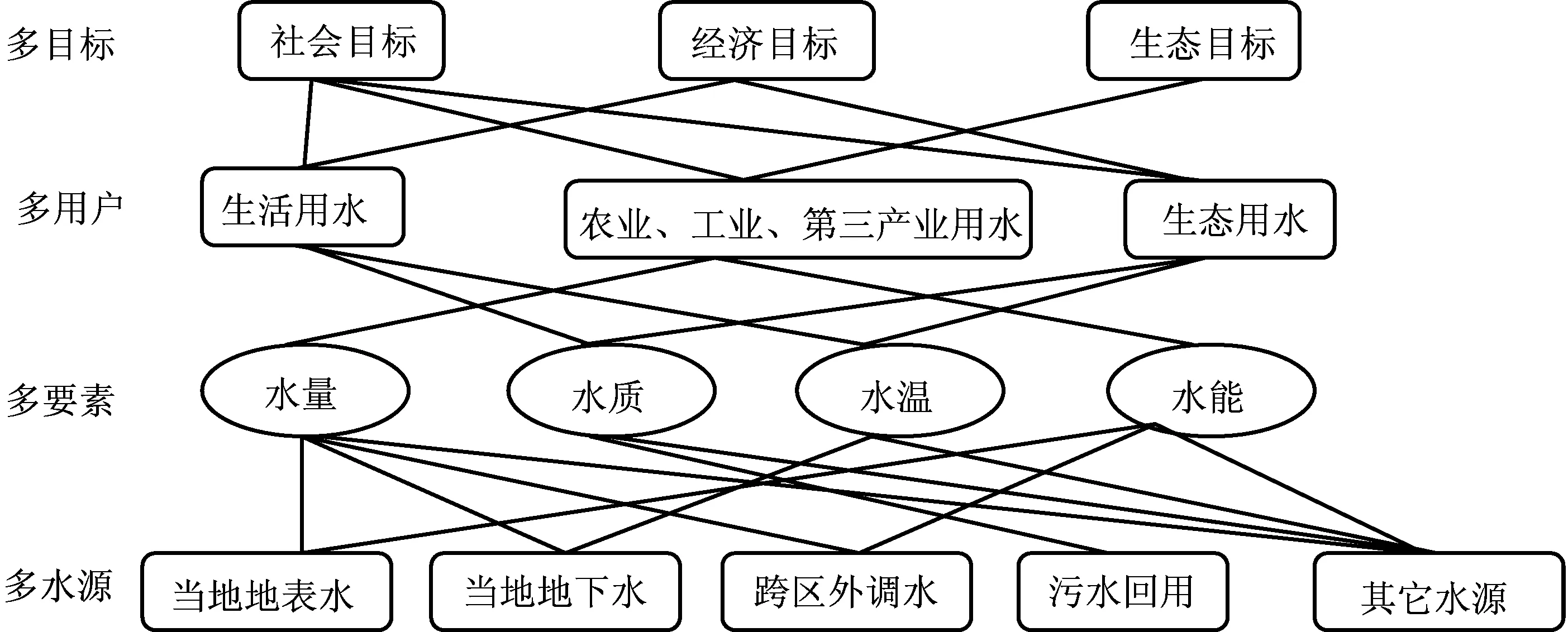
圖1 水資源優化配置屬性關系

3 線性規劃的模型

3.1 線性規劃的一般形式

所謂線性規劃,是指在一些約束條件下,求解某個具體目標最優(最小或最大)值的數學方法。其一般形式表示為[3]:

max(或min)Z=c1x1+c2x2+…+cnxn

s.t.{a11x1+a12x2+…a1nxn≤(=≥)b1

a21x1+a22x2+…a2nxn≤(=≥)b2

…,

an1x1+an2x2+…annxn≤(=≥)bn

x1,x2,…,xn≥0

3.2 線性規劃的標準形式

鑒于在內容及形式上目標函數及約束條件的不同,線性規劃問題有多種不同的表達式。因此,為了方便研究,制定了統一的算法,把線性規劃的一般形式化成標準形式[4]:

max(或min)Z=c1x1+c2x2+…+cnxn

s.t.{a11x1+a12x2+…a1nxn=b1

a21x1+a22x2+…a2nxn=b2

…,

an1x1+an2x2+…annxn=bn

x1,x2,…,xn≥0;b1,b2,…bn≥0

把一般形化為標準形的過程,可以簡而言之為“三化”:即目標最值化、約束等式化和變量非負化。

4 應用線性規劃模型優化配置水資源[5]

某供水公司給生活、農業以及工業供水,年供水最大量6500×104m3,有關信息如表1所列。供水成本和水價不同導致獲得利潤也不同,在滿足不同部門供水需求的前提下,為了獲得最大供水利潤,需要制定最佳配水方案。

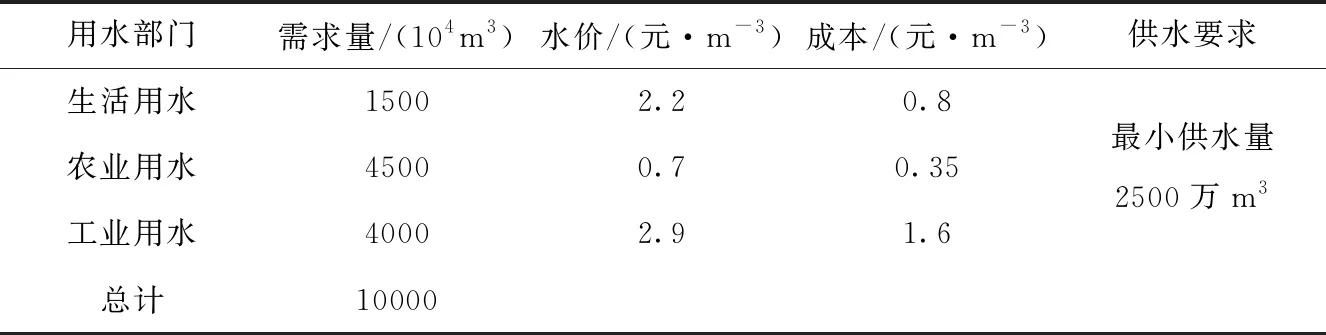
表1 供水信息

該供水公司向生活、農業、工業用水的供水量分別是X1×104m3、X2×104m3、X3×104m3目標函數為: MaxZ=(2.2-0.8)X1+(0.7-0.35)X2+(2.9-1.6)X3

約束條件是:{X1+X2+X3≤6500

0≤X1≤1500

2500≤X2≤4500

0≤X3≤4000

該模型可采用單純形法來求解,得X1=1000×104m3,,X2=3000×104m3,X3=2500×104m3,供水最大利潤為5700萬元。也可以利用LIND0軟件求解。

5 結束語

水資源優化配置目的是合理開發、高效利用水資源,促進經濟、環境的可持續發展。目前水資源嚴重缺乏,我們必須重視水資源優化配置的研究,處理好社會、資源、經濟及生態環境的關系,保證其可持續性發展。本文介紹了線性規劃在水資源優化配置具體實例中的應用,明確目標函數及約束條件,然后用線性規劃的求解方法求得最優解,在滿足各方供水要求的同時,獲得最大供水利潤。事實上,在具體的生產實際中,目標函數和約束條件通常不是線性函數,這時還要用到非線性規劃法、多目標規劃法、動態規劃法等,以達到更高要求的水資源的優化配置。