創新提問方式 提升問答效果

李健

課堂教學離不開提問，筆者在教學中創新了以下幾種提問方法。

情境提問助理解。對于一些似是而非的問題，教師借助情境提問，可直觀地幫助學生理解知識。

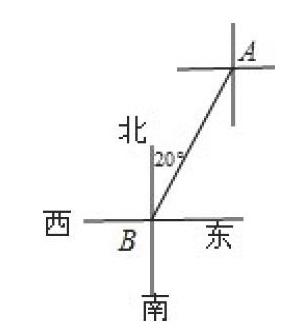
筆者在教學《方向的相對性》時，為了鞏固所學，信手拈來一題：“若A在B的北偏東20°的方向，那么B在A的???? 偏???? 的方向上？”一名成績很好的學生脫口而出：“南偏西20°。”其他學生紛紛附和。筆者又問：為什么不是北偏東或西偏北20°呢？學生說不出原因。于是筆者請5名學生走上講臺模擬出東、西、南、北、B五個方向，讓一名學生扮作A，站在與B同學北偏東20°的位置上，再讓這名學生根據自己所處的位置重新設置東、西、南、北方向，這名學生立即得出結論：根據方位角的意義畫出A點與B點的位置，然后根據圖像描述，可見B在A的南偏西20°方向上（如下圖所示）。

轉化提問尋捷徑。當教師發現學生的思考是膚淺、片面時，就要轉化提問方式引導學生就原來的問題進行深入而周密的思考。

比如，筆者教學《找一個數的因數》時，出示了這樣一道變式練習題：“18的因數有多少個？”問題一提出，學生面面相覷，束手無策。于是筆者將題目進行了轉化：“這道題表面上是要我們求因數的個數，如果我們知道了18的因數是哪些，這個題目不就很容易嗎？”一名學生應聲而答：“根據因數的概念，我們可以從小到大排列——1、2、3、6、9、18，共6個因數。”筆者追問：“有沒有更快的尋找方法？”學生通過討論發現，這道題可以用“一對一”的方式尋找，找出一個，對應的另一個也就找到了，找到了1，就可以確定對應的18，依次類推，有1，18;2，9;3，6共6個因數。

繁題簡問迎刃解。無可否認，現在的很多題目是繁難的，小學生受認知所限，很難正確回答。因此，教師要善于將繁難問題簡易化。

筆者在教學《植樹問題》時，以三月植樹節為素材創設情境：“在全長100米的小路一邊植樹，每隔5米栽一棵（兩端都要栽）。一共需要多少棵樹苗？”問題一提出，大部分學生脫口而出“20棵”。于是，筆者轉變策略，把問題簡化為“如果同學們在全長10米的小路一邊植樹，每隔5米栽一棵（兩端都要栽）。一共需要多少棵樹苗”。學生很快在練習紙上畫了出來，并回答“3棵”。筆者再問“100米的小路需要多少棵樹苗”，大多數學生都能答出“21棵”。并且能說明原因：“第一個5米兩頭都栽樹，而下一個5米開始只栽1棵樹，所以是20加1。”這樣的引導就使繁難的問題變得容易了，復雜的問題變得簡單起來了。

適時反問促思考。對于一些雖簡實難的問題，教師不能簡單地認可或否定，應該用反問語強化學生的認知，從而加深學生的理解和思考。

在教學《三角形的分類》時，筆者設計了一個小游戲：“從一個信封里露出一個直角的三角形，它是一個什么三角形？如果露出的是鈍角呢？如果是銳角呢？”一連三問，學生對答如流：“露出直角就是直角三角形;露出鈍角就是鈍角三角形;露出銳角就是銳角三角形。” “是嗎？真的嗎？真是這樣嗎？”學生聽了筆者的反問，開始沉思。筆者便讓學生模擬、討論。最后，學生一致認為：露出直角、鈍角的三角形一定是直角三角形或鈍角三角形，可銳角三角形就比較特殊了，它必須要三個角全是銳角才行。反問往往能使學生的心理為之一震，更能促使他們深入思考，反思所答。

（作者單位：棗陽市吳店鎮中心小學）

責任編輯? 吳鋒