彈性環式擠壓油膜阻尼器流固耦合計算

江志敏，高雄兵，張 鵬

（中國航發四川燃氣渦輪研究院，成都610500）

0 引言

現代航空發動機除了追求高性能和高推重比外，還要求發動機有更輕的質量和更緊湊的結構布局，這些特點會使發動機在工作轉速范圍內存在臨界轉速。所以高性能和高可靠性的燃氣渦輪發動機的研制要求轉子系統具有優良的阻尼減振器，以減小轉子系統接近臨界轉速和通過臨界轉速時的振動。這是整機動力學設計的關鍵技術之一。

近年來，國內許多學者對彈性環式擠壓油膜阻尼器（ERSFD）做了一些探索性研究。周明等[1-3]對ERSFD的減振機理進行了初步探索，建立了油膜壓力控制方程，分析了油膜力特性；周松江、趙行明等[4]對彈性環擠壓油膜系統進行了試驗研究；洪杰等[5]以燃氣渦輪發動機用ERSFD為對象，基于有限元擠壓油膜理論對ERSFD的彈性環支承剛度、油膜壓力場分布和油膜阻尼等特性進行了研究；曹磊等[6-7]推導了ERSFD的雷諾方程，通過對ERSFD數學物理模型的求解，研究了ERSFD油膜力特性。這些研究都是基于流體力學或試驗的方法對ERSFD特性進行研究。

本文引入流固耦合的計算方法，考慮彈性環變形和滑油流場的相互作用，建立3維有限元流體和結構模型來耦合求解ERSFD滑油的流動情況，獲得油膜壓力分布特性以及彈性環在復合載荷作用下的計算結果，為了解ERSFD的減振機理以及進行結構設計提供1種新的設計思路。

1 流固耦合ERSFD模型

1.1 ERSFD結構

彈性環式擠壓油膜阻尼器在傳統擠壓油膜阻尼器的基礎上增加了具有定心彈性支承作用的彈性環，彈性環內、外凸臺分別與軸承外環和限幅器接觸面配合，把整個油腔沿徑向分隔成內、外2層油腔，彈性環凸臺又分別把每層油腔沿周向分隔成多個小油腔，油腔之間通過彈性環上的阻尼孔相連通[8-15]，具體結構如圖1所示。本文以某ERSFD算例對流固耦合特性進行計算分析。

圖1 ERSFD結構

1.2 ERSFD流固耦合模型

ERSFD的流固耦合模型關系如圖2所示。從圖中可見，彈性環在油腔里被滑油包圍，其表面均是流固耦合界面。在流固耦合模型中，雖然滑油被彈性環分割成若干小油腔，但是由于阻尼孔和凸臺上間隙的存在，使得流體模型為1個聯通的流域。

圖2 ERSFD耦合關系

處理流固耦合模型時，對結構和流體分開建立模型，二者相互獨立且允許一定的公差存在，通過流固耦合界面相互聯系，并傳遞作用力。在處理模型時，一些細節的處理決定了計算邊界條件是否成立。其一，結構建模及邊界處理。在ERSFD的流固耦合計算模型中，需考慮彈性環與內軸徑、限幅外環之間的裝配關系，并且定義接觸，給定1個合適的接觸容差范圍，模擬彈性環受到不平衡力擠壓作用時與內、外剛性結構的真實接觸關系。文中彈性環內、外實際裝配間隙均設置為0.06 mm。其二，流體模型與流固耦合邊界處理。彈性環與內軸徑、限幅外環之間的所有空隙均為ERSFD中流體的部分，包括凸臺上方的0.06 mm裝配間隙。在建立流固耦合邊界時，需要在所有流體和結構產生交互的界面上建立流固耦合方程。所以，在ERSFD實際工作過程中，流體的流動通道不止阻尼孔，還包括凸臺上方的裝配間隙，在不平衡力作用下，結構之間的接觸導致流體的流動變得復雜。ERSFD的流體和結構有限元模型分別如圖3、4所示。

圖3 流體部分有限元模型

圖4 結構部分有限元模型

1.3 流固耦合計算條件

假設激勵為內軸頸隨時間逐步增大到最大偏心距后做穩態公轉運動。計算流體和結構模型中的時間積分必須是相容的，計算均收斂于同一時間載荷步，內軸頸偏心距隨時刻的初始輸入激勵如圖5所示。內軸頸公轉2圈，轉速為10000 r/min，第1圈其偏心距幅值由0逐步增大到最大值。

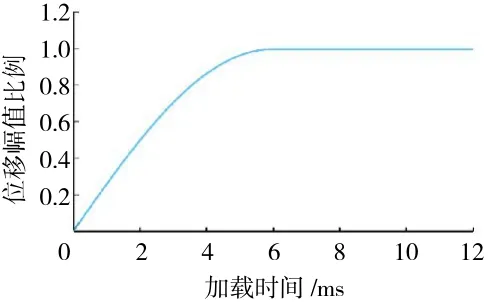
圖5 ERSFD響應計算輸入激勵

2 流固耦合特性計算結果

2.1 彈性環計算結果

通過流固耦合方法計算得到在內軸頸公轉及滑油壓力共同作用下彈性環的變形結果及振動應力的分布情況。

在傳統彈性環強度計算中，無法考慮到ERSFD中流場壓力的作用，只能得到彈性環受內軸承偏心載荷下的靜強度計算結果。在ERSFD實際工作過程中，油膜壓力會導致剛性較弱的彈性環發生變形。如算例中，不平衡力作用于正上方位置時，彈性環的變形結果對比如圖6、7所示。從圖中可見，考慮流體壓力作用后彈性環的變形要比單一機械載荷作用復雜很多，其變形量也要比單一機械載荷作用時的大。由彈性環的變形結果對比可知，在受到機械擠壓力作用的位置，采用流固耦合方法和傳統固體力學方法計算得到的變形分布及變形量值基本相當。采用流固耦合方法計算考慮了油膜對彈性元件的作用，圖中在油膜壓力較大的位置，彈性環受到擠壓而變形。

圖6 流固耦合計算得到的彈性環變形

圖7 機械載荷作用下的彈性環變形

彈性環受到相同強迫位移作用下的等效應力如圖8、9所示。從圖中可見，流固耦合計算得到的等效應力大于僅考慮機械載荷得到的計算結果，且能考慮到流體對阻尼孔的沖壓作用，其最大等效應力的位置出現在阻尼孔附近。通過流固耦合分析，ERSFD中彈性環的高周疲勞源很可能出現在阻尼孔周邊。

圖8 流固耦合計算彈性環等效應力分布

圖9 僅受機械載荷彈性環等效應力分布

為了更好的理解彈性環的變形及應力分布特征，對ERSFD的流體部分的壓力特性及流動特性進行分析。

2.2 壓力分布

通過流固耦合計算得到了內軸頸以穩定的偏心率運動到相位差為90°的4個位置時油膜壓力的分布。4個位置與進油口的位置關系如圖10所示；假設轉子的振動幅值達到0.5偏心率時，軸頸分別擠壓與進油口位置成90°、180°、270°、360°時油膜沿圓周的分布如圖 11 所示。

圖10 讀取油膜壓力位置關系

在ERSFD內軸頸偏心力作用下，油腔內的滑油被擠壓后，滑油通過阻尼孔和間隙向壓力更小的油腔流動。由于彈性環本身剛度較弱，在內軸頸偏心擠壓作用下也會變形，由此可知ERSFD的滑油流場受到內軸頸偏心擠壓及彈性環變形的共同影響。

圖11 軸頸擠壓與進油口成不同角度時油膜壓力沿圓周分布

通過流固耦合方法計算得到油膜壓力的特點如下：

（1）油膜壓力分布總趨勢與SFD的相似，但呈階梯式分布；

（2）相鄰油腔之間的壓力梯度差主要來自于阻尼孔處的節流作用；

（3）由于進油壓力的設置，軸頸運動在不同偏心角時，油膜壓力分布特點各不相同；

（4）單個油腔內由于周向黏性阻尼作用也會產生一定的壓力梯度。

2.3 滑油速度計算結果

通過流固耦合計算得到ERSFD中滑油的速度矢量分布如圖12所示；油膜阻尼孔截面局部的流體矢量如圖13所示；ERSFD軸向剖面內、外油腔壓力分布及壓力差如圖14所示，滑油流動情況如圖15所示。

從圖12中可見，ERSFD油膜阻尼的滑油流動速度較大的部位有2處：凸臺與限幅外環、內軸頸之間間隙處的周向流動和阻尼孔處的徑向流動。

圖12 ERSFD阻尼孔截面滑油速度矢量

圖13 ERSFD6點鐘位置流體矢量

圖14 ERSFD軸向截面滑油壓力分布

圖15 滑油流動

通過對ERSFD速度矢量以及阻尼孔處滑油流動特點的分析可知ERSFD阻尼孔在減振中的作用：內軸頸公轉壓迫滑油，滑油進入阻尼孔和凸臺間隙后，由于慣性流束將繼續收縮直至縮頸的最小截面流速增大，然后又逐漸擴大，直至碰撞到限幅外環或內軸頸的表面。在縮頸附近的流束與阻尼孔壁之間以及滑油流出阻尼孔后的拐角與流束之間都有1個充滿小漩渦的低壓區。漩渦靠主流束帶動著旋轉，主流束把能量傳遞給漩渦，漩渦又把得到的能量耗散在旋轉運動中，變成熱而散逸，形成明顯的節流損失，把振動能量轉化為熱能。

3 結論

（1）在不平衡力及油膜壓力的共同作用下，ERSFD中彈性環的變形變得復雜，其變形量大于僅受到不平衡力作用下的變形量；

（2）ERSFD中彈性環上的應力集中位置除了凸臺倒圓處外，還有阻尼孔的孔周，對于彈性環高周疲勞設計時還需要對阻尼孔截面開展評估分析；

（3）ERSFD油膜壓力沿圓周分布呈階梯型變化，總趨勢宏觀上與SFD分布都呈類似正、余弦趨勢分布，但是減振機理已發生改變；

（4）ERSFD的阻尼主要由彈性環阻尼孔和凸臺間隙處滑油的高速流動形成的節流損失產生。