信道狀態信息指紋定位算法性能評價方法研究

蔣天潤，尹 露，鄧中亮，王子陽

(北京郵電大學電子工程學院，北京 100876)

0 引言

室外條件下，用戶使用的定位設備主要基于全球定位系統(Global Positioning System，GPS)。由于室內的接收機受到建筑物的遮擋，使得接收到的衛星定位信號衰減很快，甚至完全無法接收到信號。隨著移動設備和無線傳感器的大量部署，關于室內有源主動定位的研究取得了長足發展，但它在室內定位時需要人攜帶有關的傳感器設備，使得有源定位的廣泛應用受到較大阻礙。

隨著移動互聯網技術的迅速發展，人們對于獲得高精度位置信息的需求愈加強烈，未來室內定位將成為一項生活所必須的基本服務需求。目前，室內定位技術種類繁多，主要有基于射頻識別(Radio Frequency Identification，RFID)、超聲波、紅外線和WiFi等的室內定位技術[1]。RFID定位需要提前布置硬件設備，實現大范圍推廣的成本很高[2]。紅外定位技術的精度會受到室內燈光、熱源的影響，另外室內的各種障礙物也會遮擋紅外線，導致紅外線不能傳輸很遠的距離，以及定位誤差增大[3]。由于超聲波在空氣中傳播時衰減速度很快，距離稍遠超聲波定位技術的定位誤差就會迅速增大。無線局域網已在人口密集區域廣泛普及，各處的室內都大量部署了無線上網設備，基于WiFi的室內定位技術具有定位耗時短、覆蓋面積大、成本低等優點，因此該技術成為了室內定位研究領域的熱點方向。

目前基于WiFi的室內定位研究主要基于接收信號強度指示(Received Signal Strength Indicator，RSSI)。RSSI描述了接收信號功率的大小，由于目前多數終端設備都支持獲得RSSI信息，故目前的無線通信技術都使用RSSI作為評價信道質量的標準，從而改進通信系統。基于WiFi的RSSI指紋定位法將處理后的RSSI作為每個位置的指紋特征，從而開展基于位置指紋庫的指紋定位。RSSI是多條路徑信號的簡單疊加[4]，因此RSSI并不能充分描述子信道受環境的干擾程度。此外，盡管單個信道的信號波動較小，但多條信道中信號疊加的RSSI波動范圍甚至達到了5dB[5]。單一使用RSSI作為信號特征進行指紋定位不能滿足高精度、高穩定性的室內定位需求。

相較于RSSI，信道狀態信息(Channel State Information，CSI)能夠更好地描述多徑信道，區分來自多個信道的多徑信號，在靜態環境下具有較好的穩定性。CSI的一個數據分組中同時包含著多個子載波的幅頻響應和相頻響應。在室內定位中以子信道的多維矩陣對單一的RSSI進行擴展來構建格點特征，由此可以獲得更高的定位精度。近年來，Inter和Atheros網卡供應商對其部分網卡固件程序進行了處理，并有相關組織開源了對應的軟件開發包，使得可以對Linux系統以及Windows系統下的網卡開源驅動程序進行修改，利用調試模式來獲取某些無線網卡的CSI數據。使用大量部署的基于802.11n標準的WiFi路由設備可以獲得CSI[6]。基于CSI的指紋定位需要的額外硬件設備較少，實現成本低，具有廣泛的應用前景。

1 CSI與指紋定位算法

1.1 信道狀態信息

目前，使用裝配Intel 5300網絡適配器的普通WiFi設備能夠獲得一個采樣個數為30的CSI信息，利用兼容IEEE802.11.n的無線網卡從接收的數據包中提取一組CSI，每組CSI代表一個正交頻分復用子載波的幅度與相位,如式(1)所示

(1)

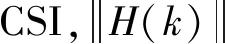
1.2 指紋定位法

指紋定位法主要包括2個階段。離線訓練階段即數據采集和處理過程，該過程主要工作是采集格點信息，將該信息處理后構建為格點特征，常用的格點特征包括相位和幅度等；實現格點位置與格點特征的映射；建立無線地圖和指紋定位數據庫。

在在線定位階段，實時采集待定位點的格點特征，輸入至定位服務器，服務器將定位端實時上報的數據與離線階段建立的位置指紋庫的數據進行匹配，計算出實時數據最佳匹配的參考點。在線階段的主要思路是依賴一定的準則選擇與實時數據最為接近的參考點。

1.3 研究現狀

文獻[7]表明WiFi的CSI具有更高的時間穩定性，并具有從多徑效應中獲益的能力，因此適用于準確的存在檢測和定位。文獻[8]表明由于室內環境的復雜性對多徑信號傳播的影響，難以建立精確的信號傳播模型，因此基于CSI的指紋定位法優于基于傳統傳播模型的室內定位方法。文獻[9]基于CSI的子信道頻率的不同，用合并且求均值后的5個子載波的CSI代替原來的30個子載波的CSI，并對多根天線的CSI求平均值處理，提出了一種基于后驗概率的指紋定位算法。Qian K.等[10]利用CSI導出運動誘發的多普勒頻移，并提取出該頻移用于確定運動方向。

2 采集CSI信息與制作指紋庫

在北京郵電大學的新科研樓內選擇一間10m×10m的實驗室，室內放置有大量物品以及人員走動。根據地磚將室內劃分成1m×1m的方格，在每個參考點測量CSI數據，每個格點的CSI數據存儲在若干個數據包中，如圖1所示。

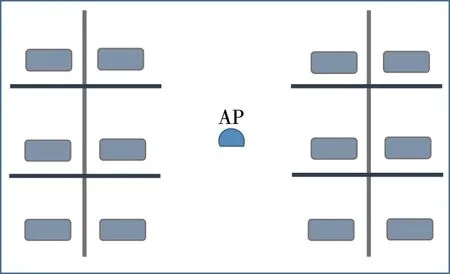
圖1 數據采集環境示意圖Fig.1 Data collection environment

經過上述操作獲得的原始CSI數據含有高頻噪聲，需要對原始CSI數據進行低通濾波處理。使用h表示該巴特沃斯濾波器的傳遞函數。單個數據包中的CSI數據為H(1*30)，濾波后的矩陣記為H′(1*30)

H′=h*H

(2)

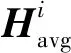
(3)

3 算法關鍵參數的測試與分析

3.1 測試KNN與wKNN算法

K最近鄰(K-Nearest Neighbor，KNN)算法，K表示距離自己最近的k個數據樣本[11]。KNN算法使用的相似度量是曼哈頓距離或歐式距離，該算法所選擇的鄰居都是已經正確分類的對象。該算法在定類決策上只依據最鄰近的一個或者幾個樣本的類別來決定待分樣本所屬的類別。

在實際的生產實踐中，KNN算法的缺陷是找到的近鄰并不是實際意義上的近鄰。特征向量之間一般有較大可能性是相關的，最近距離的求解過程中沒有考慮特征之間的關系，故距離的計算不夠準確，從而影響了定位的準確度。為了解決以上問題，使用加權K最近鄰(weighted K-Nearest Neighbor，wKNN)算法[12]。

將每一鄰居樣本的坐標與對應權重相乘，結果相加[13]，求出總和后，將結果除以全部權重之和。估計坐標的計算方法如式(4)所示

(4)

式中，Di表示鄰居樣本的坐標，wi表示近鄰樣本的權重，f(x)是預測的坐標結果。

wi=1/(distance+const)

(5)

式中，權重wi是距離數值加上一個常數的倒數。

在圖2和圖3中，藍色虛線代表了測試所走過的真實路徑，*號代表在藍色真實路徑上均勻取點所對應的定位結果。在K=5，離線指紋庫容量為100，在線數據集容量為35時，KNN定位誤差是2.732m，wKNN定位誤差是2.651m。

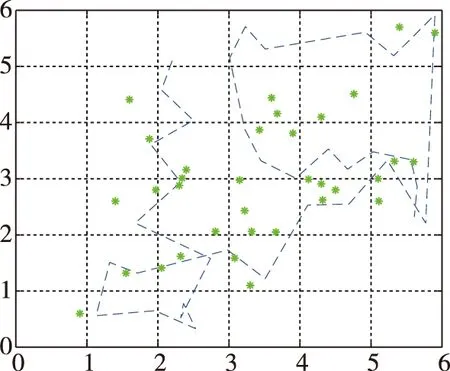
圖2 KNN定位結果圖Fig.2 The locating result of KNN algorithm

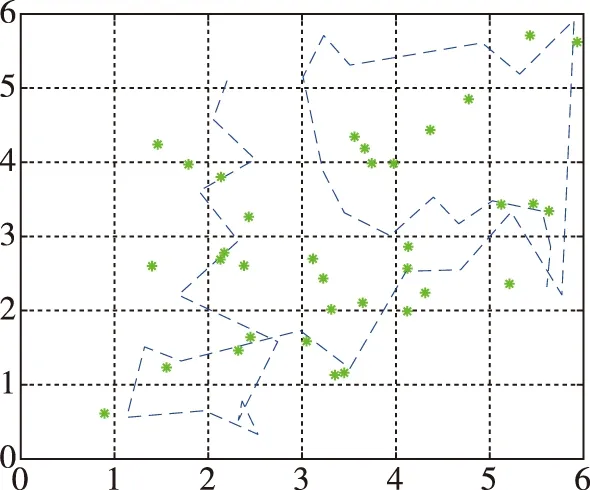
圖3 wKNN定位結果圖Fig.3 The locating result of wKNN algorithm

在離線數據集容量為100,在線數據集容量為35時，改變K值，觀察其對定位誤差的影響。

從圖4可以看出，兩種算法的定位誤差隨K的變化曲線有一定的相似性。在K<9時，兩種算法的定位誤差隨K的增大而減小；在K>9后，兩種算法的定位誤差隨K的增大反而逐漸增大，但此時的最大定位誤差仍小于K<9時的最大定位誤差。

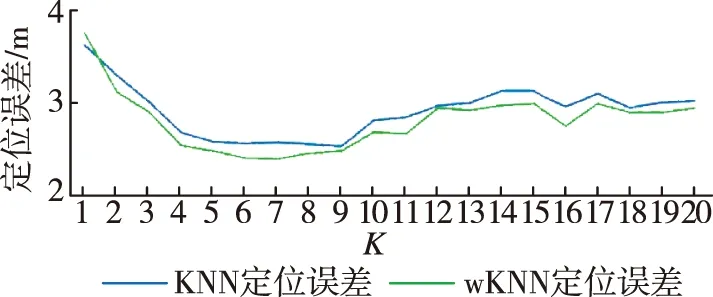
圖4 兩種算法定位誤差隨K值變化圖Fig.4 The tendency chart of positioning error with K

OFDM系統中的每個子信道是相互獨立的[14]，在CSI中，理論上每個子信道的幅度也是相互獨立的，即在本次測試中理論上各特征向量之間是不相關的。因此，使用wKNN算法對定位精度的改善有限，這也解釋了以上兩種算法的定位誤差隨K的變化趨勢較為相似的原因。

較小的K值會導致鄰居不夠，定位精度受此影響[15]，因此K<9時定位誤差隨K的變化趨勢如上所示；但是過大的K值會導致不屬于同一類的點也被分入鄰居內，使得定位誤差增大，這是K>9后定位誤差隨K增大而增大的原因。

4 三種算法穩定性測試與分析

4.1 算法評價指標與樣本集擴充方法

通常評價一種定位算法性能的依據是該算法的定位精度，但該評價依據并沒有考慮到在線測量數據增加時，該種算法的穩定性問題。因此本文提出了一種評價KNN、wKNN和隨機森林算法優劣的依據：三種算法定位時間的穩定性和定位精度的穩定性。

某種算法的運行時間在一定程度上反映了該算法的計算量和資源占用的多少，由于算法的運行時間具有一定的時變性和不穩定性，選取運行時間的標準差占平均運行時間的百分比作為評價標準。定位精度的穩定性可以直接使用在線樣本容量為100～20000時定位精度的平均值與標準差進行評價。

如果將10m×10m的辦公區域劃分為0.5m×0.5m的方格，則指紋庫中最多只有400個點的指紋信息。0.5m的方格長度相較于超過2m的定位誤差很小，可以認為在該10m×10m的區域中，至多只存在400個定位結果，那么，在線數據集所有可能點的坐標都在這400個點中產生。因此，樣本容量的擴充方法如圖5所示，將新的在線樣本集逐個編號，每次從以上的原始樣本集中隨機取樣，重復400次，將400個取樣結果全部用來擴充原始樣本集，將擴充的結果作為新樣本集，直至樣本容量符合實驗要求。

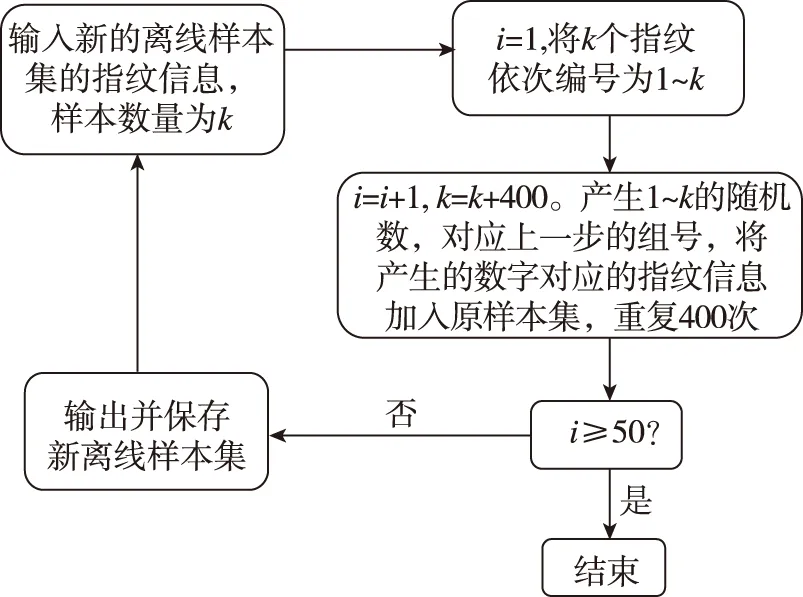
圖5 樣本集擴充方法Fig.5 Sample capacity expansion method

4.2 穩定性測試與分析

測試軟件均使用Pycharm。在線數據集的樣本數量為100～20000。KNN與wKNN算法中K=6，隨機森林算法中決策樹數量為110，max_features=0.45，max_depth=15。

從圖6和表1中可以看出，根據定位誤差的標準差對比，隨機森林算法的定位誤差的波動性最小，KNN算法最大。在樣本容量逐漸增加的過程中，隨機森林算法定位誤差最為穩定。同時，隨機森林的定位誤差最小，性能也最好。

從三種算法運行時間的標準差占平均運行時間的百分比來看，隨機森林是3.67%，wKNN是5.31%，KNN是9.87%。隨機森林的運行時間穩定性要高于KNN和wKNN算法。

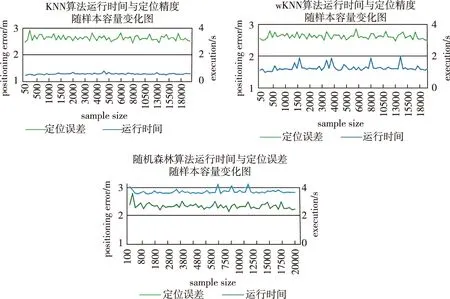
圖6 三種算法運行時間與定位誤差隨樣本容量變化圖Fig.6 The tendency chart of positioning time and positioning error with sample size of three algorithms

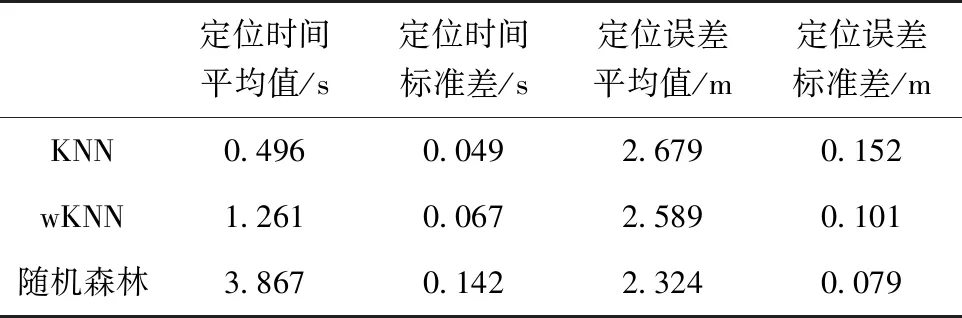
表1 三種算法評價指標對比

5 結論

1)本文介紹了CSI和指紋定位法的概念，分析了使用CSI進行指紋定位的優勢，闡述了指紋庫的構建過程和定位方法。

2)分析了KNN和wKNN算法中關鍵參數K對定位誤差的影響。結果表明，在K較小時，增大K可以使用更多相關鄰居來計算定位結果，進而提高定位精度；但過大的K值會導致原本不相關的鄰居加入鄰居隊列，也會使定位誤差增大。

3)在線樣本集容量增加時，測試了KNN、wKNN和隨機森林算法的運行時間和定位精度的穩定性，結果表明，隨機森林算法不僅定位精度最高，而且定位時間與定位精度的穩定性最好。