TiO2摻雜粒度對纖維素強度和熱穩定性影響的分子模擬研究

王成江，劉玉斌，梅侶松，趙一帆，李亞莎

(三峽大學 電氣與新能源學院，宜昌443002)

1 引 言

電力變壓器是電力系統中最核心的電氣設備，在電能的傳輸過程中起著至關重要的作用，變壓器絕緣紙的主要成分是纖維素，其具有較高絕緣要求. 廖瑞金、呂程等[1, 2]通過真空浸油測試實驗研究了納米TiO2摻雜絕緣紙的絕緣性能，研究表明納米TiO2摻雜絕緣紙的工頻擊穿場強有所提高，相比于未摻雜的絕緣紙提高了20.83%. 絕緣性能不僅由電學性能決定，材料的強度和熱穩定性也影響著絕緣紙的絕緣性能. 在很多情況下，絕緣失效是由材料的強度和熱學及環境造成的[3]. 為了保證電力系統安全穩定運行，提高變壓器絕緣紙的強度和熱穩定性具有十分重要的意義.

近年來，分子模擬方法已廣泛應用到變壓器絕緣性能研究[4]，Tang和Zhang等人[5, 6]利用納米SiO2、Al2O3摻雜纖維素，通過分子模擬研究SiO2和Al2O3摻雜纖維素的力學性能和兼容性等方面，從微觀角度闡述納米SiO2和Al2O3粒子對纖維素摻雜的作用機理.

納米摻雜聚合物使得形成多界面復合體系，當摻雜顆粒的粒度降低到納米尺度，聚合物/納米顆粒的相關特性有全面的提升. 孫偉峰和王暄[7]利用分子模擬研究PI/Cu納米顆粒復合物的熱力學性質和力學特性，研究發現PI/Cu納米顆粒復合物的熱力學性質表現出顯著的粒度效應. 謝驚宇[8]利用不同半徑SiO2粒子對間位芳綸力學性能和熱穩定性進行研究，納米SiO2與間位芳綸纖維素間的結合能隨納米粒度的增加而增大；間位芳綸纖維素的強度和熱穩定性隨著納米SiO2粒度不同表現出明顯的粒度效應.

目前，不同納米TiO2摻雜粒度對纖維素強度和熱穩定性影響的研究甚少，本文將采用分子模擬從微觀角度分析不同納米TiO2粒度對纖維素的影響，探索納米TiO2摻雜粒度對纖維素強度與熱穩定性的提升機理及其變化規律，從而為納米TiO2摻雜纖維素的制備工藝提供理論支撐.

2 模型的建立及仿真細節

2.1 模型的建立

絕緣紙的主要成分為纖維素，其主要有晶體區和無定型區兩種存在形式，由于纖維素晶體區相對于無定形區比較穩定不易受到損壞，故利用不同納米TiO2粒度摻雜纖維素時優先考慮無定型區. 纖維素的重復單元為葡萄糖二糖，纖維素的分子鏈結構式如圖1.

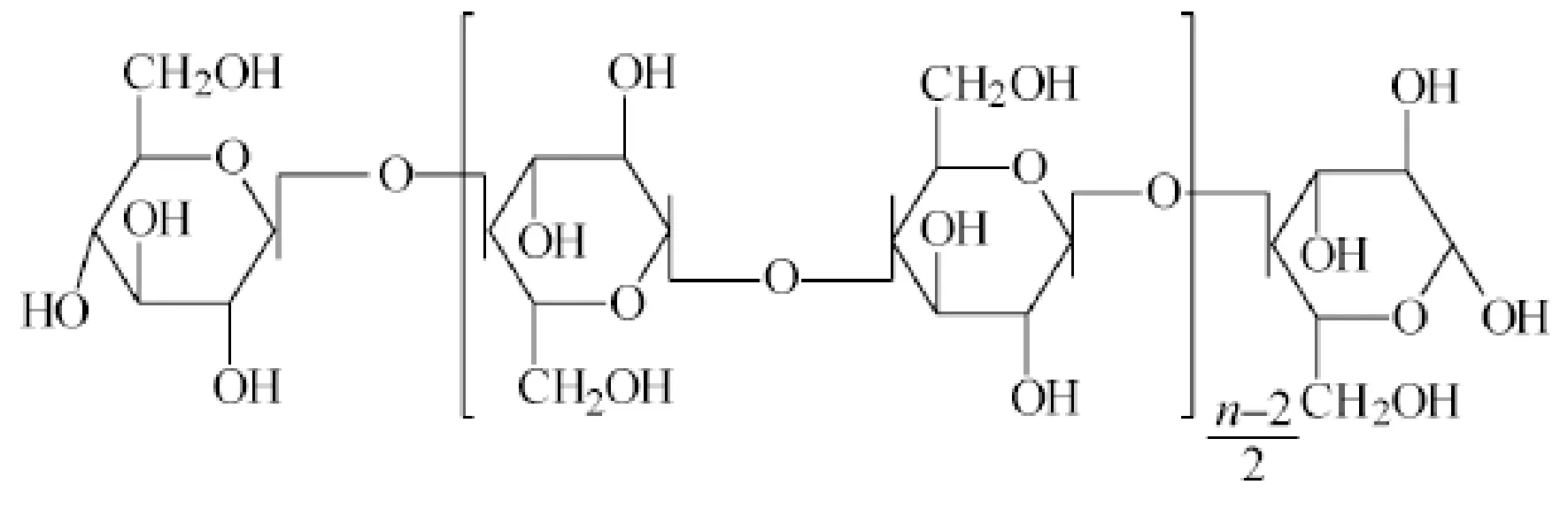
圖1 纖維素的分子鏈結構式Fig. 1 Molecular chain structure of cellulose

Mazcau等[9]發現纖維素鏈長度在分子構象和理化性質上并沒有表現出明顯差異，本文由于受到計算機性能的局限，為計算方便，將采用聚合度為10的纖維素進行建模. 利用多尺度建模方法構建未摻雜納米TiO2和摻雜不同納米TiO2粒度(2 ?、3 ?、4 ?、5 ?、6 ?、7 ?)的纖維素無定型模型，并保持摻雜體相同的質量分數，即為3%. 通過MS中AC|Packing將聚合度PD=10的纖維素封裝為基體，其模型的目標密度均設為1.5 g/cm3[10]，再利用 AC |Calculation將納米TiO2團簇嵌于基體中間，其構建模型如圖2所示.

圖2 未摻雜纖維素與摻雜納米TiO2纖維素模型Fig. 2 Undoped cellulose and doped Nano-TiO2 cellulose models

2.2 模擬細節

為了使7組模型能量處于較低狀態，先對7組模型分別進行分子動力學弛豫使得體系能量處于較低狀態，在此基礎上進行目標溫度下的分子動力學模擬. 在模擬過程中，考慮到電力變壓器常處于正常運行溫度和受環境、負載等諸多外界因素影響時局部溫度過高，故本文選取的模擬溫度為70～150 ℃. 每個體系進行100 ps的平衡模擬，系綜設置為NVT，在相同的目標溫度下又進行100 ps的分子動力學模擬，系綜設置為NPT，待體系達到平衡后，在同樣的溫度下進行200 ps的分子動力學模擬，系綜設置為NPT，積分步長均設置為1 fs，壓強設置為0.001 GPa，體系內各原子的動力學信息每隔500 fs收集一次，以用于分析.

整個模擬流程均采用COMPASS力場，此力場已經被證實非常適合計算有機和無機分子構成的體系. 溫度控制采用Anderse熱浴法，壓強控制采用 Berendsen壓浴法，并用velocity verlet跳蛙算法進行牛頓運動方程求解. 對于非鍵相互作用，范德華作用采用Atom Based方法，靜電作用采用Ewald法.

3 強度的表征與分析

3.1 強度的表征

纖維素作為電力變壓器內部絕緣紙的主要成分，其具有較高的強度. 通常利用拉伸模量(E)、體積模量與剪切模量的比值(K/G)、泊松比(γ)和柯西壓(C12-C44)等微觀參數表征強度. 由彈性力學可知，固體材料的應力-形變之間的關系可以用廣義Hooke定律[11]表示：

式中σ為應力、τ為切應力、ε為應變、γ為切應變. 拉梅系數λ、μ和強度參數均可由以下推到公式得出：

(1)

(2)

(3)

(4)

(5)

G=μ

(6)

強度微觀參數的定義：拉伸模量(E)為應力與應變的比值，是度量材料鋼性的參數，拉伸模量與材料的鋼性成正比，拉伸模量越大，材料的鋼性越強；體積模量與剪貼模量的比值(K/G)用于評價材料的韌性，其值越大表明材料的韌性越好；泊松比(γ)為橫向應變與縱向應變的比值，反映材料橫向變形的彈性常數，其值越大材料的可塑性越強；柯西壓(C12-C44)用于衡量材料的延展性，其值越大材料的延展性越強，其值越負材料的脆性越強.

3.2 摻雜納米TiO2對纖維素強度的影響

圖3左坐標表示70 ℃～150 ℃下未摻雜和摻雜納米TiO2纖維素的拉伸模量變化趨勢，納米TiO2摻雜纖維素的拉伸模量比未摻雜模型整體偏大. 隨著溫度升高，摻雜TiO2纖維素的拉伸模量減小的幅度比未摻雜納米小，可見，納米TiO2摻雜纖維素使得拉伸模量隨溫度的升高而減少的幅度較小，納米TiO2使得纖維素形變難度加大，抗形變能力加強. 圖3右邊的坐標軸為K/G，摻雜和未摻雜TiO2纖維素均表現出相同的變化趨勢，即先增大后減小再增大，在90 ℃和130 ℃時達到最大. 從整體圖形看，納米TiO2摻雜纖維素的K/G均比未摻雜的值大. 摻雜納米TiO2使得纖維素韌性有較大的提升. 綜上微觀強度參數對比分析，摻雜納米TiO2使得纖維素的強度得到提升.

圖3 未摻雜、摻雜模型的拉伸模量、K/G值Fig. 3 Tensile modulus and K/G values of undoped and doped models

3.3 納米TiO2摻雜粒度對纖維素強度的影響

考慮到納米TiO2對纖維素的強度影響，摻雜不同納米TiO2粒度對纖維素的拉伸模量、泊松比和柯西壓等微觀參數進行分析. 圖4表示摻雜不同納米TiO2粒度纖維素的拉伸模量和泊松比在70 ℃、90 ℃下的變化趨勢. 由圖可知拉伸模量和泊松比在70 ℃和90 ℃時的變化趨勢均相同，即拉伸模量隨納米粒度增加逐漸減小，泊松比隨納米粒度增加逐漸增大. 不同納米TiO2粒度摻雜纖維素在溫度的影響下出現相同的變化趨勢，故可以選取一個溫度進行不同納米粒度對纖維素的影響研究.

在70 ℃下，隨著納米TiO2粒度增加，拉伸模量呈減小趨勢，納米TiO2摻雜纖維素的強度逐漸減小，抗形變能力減弱. 隨著納米TiO2粒度增大，納米TiO2摻雜纖維素的泊松比增大，纖維素的可塑性增強，在外力和應力的作用下容易發生形變，使得材料的鋼性減弱，強度降低. 圖3可以得出，納米TiO2摻雜纖維素的拉伸模量和柯西壓均出現粒度效應，當納米TiO2粒度越小，摻雜納米的纖維素的拉伸模量越大和泊松比越小，抗性變能力越強，材料的強度越好.

圖4 不同納米TiO2粒度的拉伸模量、K/G值Fig. 4 Tensile modulus and K/G values of different Nano-TiO2 granularities

圖5為摻雜不同納米TiO2粒度的纖維素在70 ℃、90 ℃時的柯西壓值，隨著納米TiO2粒度增大，纖維素的柯西壓值呈減小趨勢. 納米TiO2半徑為2.0 ?時，納米TiO2摻雜纖維素的柯西壓最大，其值為3.0 ?左右，當納米TiO2半徑逐漸增加到7.0 ?時，柯西壓值隨著半徑增大逐漸減小，由此證明，摻雜納米TiO2可以提升纖維素的柯西壓值，納米粒度越小，纖維素的柯西壓值越大，材料的延展性越強，材料發生形變而不產生裂紋的能力越強.

圖5 不同納米TiO2粒度的柯西壓Fig. 5 Cauchy pressure of different Nano-TiO2 particle sizes

3.4 機理分析

摻雜不同粒度納米TiO2對纖維素的拉伸模量、泊松比和柯西壓均有一定提升，其作用機理：納米TiO2粒度越小，納米TiO2越容易分散于纖維素中，小納米粒度團簇的比表面積大，其表面O與H原子形成的表面羥基易于纖維素形成氫鍵，使得納米TiO2與纖維素緊密形成復合體系，基體纖維素受到張力作用，納米粒子與基體之間會產生銀紋，基體纖維素也產生塑性形變，吸收一定的張力，由于無機納米粒度比較小、比表面積相對較大，納米TiO2與基體纖維素間接觸面也就比較大. 當纖維素受到外來張力時會產生更多銀紋及塑性形變，并吸收更多張力從而達到增韌效果. 納米TiO2與纖維素緊密結合，一部分載荷被納米TiO2承擔，從而使得纖維素的抗張強度增加.

4 熱穩定性的表征與分析

4.1 熱穩定性的表征

電力變壓器長期運行在高溫條件下，纖維素作為絕緣紙的主要成分需要具有較高的熱穩定性，溫度過高會使纖維素發生強烈的鏈運動，使得結構遭到破壞. 通常利用徑向分布函數、自由體積和均方位移表征纖維素的熱穩定性.

徑向分布函數(RDF)用來分析纖維素間的氫鍵數目的變化情況，表征纖維素的氫鍵結合程度. 徑向分布函數峰值越大，體系氫鍵數越多，體系就越穩定，材料的熱穩定性越好.

均方位移描述鏈的整體移動情況，纖維素的鏈運動很大程度上影響著纖維素的熱穩定性. 纖維素的鏈運動越劇烈，纖維素的熱穩定性就越差，其均方位移(MSD)的表達式[12]為：

(7)

通過Fox和Flory的自體積理論[12]闡述纖維素的熱穩定性，其理論：材料的總體積分為兩部分，即占有體積(Occupied Volume，VOV)和自由體積(Free Volume,VFV)，占有體積表示該部分被分子占據的體積，自由體積表示為該部分未被占據的體積，也稱空隙，則自由體積分數(fFFV)推導公式：

(8)

式中，fFFV為自由體積分數，VFV為自由體積，VOV為占有體積.

自由體積分數為自由體積占總體積的比重，自由體積分數越小，材料的內部空隙就越小，纖維素鏈在分子層面不容易發生鏈運動，材料結構相對穩定，受溫度的影響較小，熱穩定性較強.

4.2 摻雜納米TiO2對纖維素熱穩定性的影響

圖6(a)(b)表示未摻雜和摻雜納米TiO2纖維素的徑向分布函數(RDF)，未摻雜和摻雜納米TiO2纖維素的徑向分布函數在0.097 nm附近出現強烈的峰值. 由于徑向分布函數的主圖線條太密集，故將0.208-0.26 nm的RDF圖形放大，如局部圖所示，在0.208 nm和0.245 nm附近出現中等強度的峰值，此范圍正好處于纖維素中的氧原子與納米TiO2的表面羥基形成氫鍵的范圍. 圖6(a)(b)中的局部圖0.208～0.245 nm范圍的峰值對比發現納米TiO2摻雜纖維素在各個溫度下的RDF均比未摻雜的纖維素峰值大. 為更清楚地觀察摻雜之后的變化情況，本文把70 ℃時未摻雜和摻雜納米TiO2纖維素的徑向分布函數進行對比分析，如圖6(c)所示.

(a)未摻雜TiO2纖維素的RDF

(b)摻雜TiO2纖維素的RDF

由圖6(c)可知，納米TiO2摻雜纖維素在0.208 nm和0.245 nm處的RDF峰值均比未摻雜的RDF峰值大，纖維素中H與TiO2中O形成氫鍵，從而增加纖維素與TiO2復合體系的氫鍵數目. 由圖6(a)(b)可以看出，隨著變壓器運行溫度升高，纖維素在0.2 nm～0.26 nm之間中等強度的峰值趨于減小，90 ℃～150 ℃的RDF均比70 ℃的RDF小. 研究表明纖維素出現鏈老化趨勢，纖維素分子間的氫鍵數目相對減少. 納米TiO2摻雜的纖維素同樣會隨著溫度的升高，出現鏈老化的情況，但由圖6(c)的中等強度峰值對比發現，納米TiO2摻雜纖維素的氫鍵數目隨溫度升高減小的程度小于未摻雜納米TiO2中氫鍵數目減小的程度.

4.3 納米TiO2摻雜粒度對纖維素熱穩定性的影響

考慮到納米TiO2對纖維素熱穩定性的影響，通過摻雜不同納米TiO2粒度對纖維素的熱穩定性進行分析. 通過Fox和Flory的自體積理論和分子運動理論可知，空隙是材料中微觀粒子運動的原因，因此可以用自由體積理論解釋絕緣材料的熱穩定性. 利用硬球探針法計算自由體積的，纖維素的硬球半徑無法獲得，在此利用范德華半徑為硬球探針. 通過MS軟件分析不同粒度的納米TiO2摻雜纖維素的自由體積，其具體數據如表1.

表1 不同納米TiO2尺寸摻雜纖維素的自由體積(VFV)、占有體積(VOV)和自由體積分數(FFV)

Table 1 Free volumes, occupying volumes and free volume fractions of celluloses doped with different Nano-TiO2sizes

RVOVVFVFFFV2?4988.23?2651.53?20.1163?9802.86?21436.56?20.1284?17259.08?25166.69?20.1355?40014.25?210638.75?20.2106?17345.59?263275.98?20.2157?29479.47?288891.30?20.249

表1為不同納米粒度摻雜纖維素的占有體積、自由體積和自由體積分數. 從自由體積分數可以看出，隨著納米TiO2粒度逐漸增大，纖維素的自由體積分數逐漸增大，其模型的自由體積逐漸增大. 小粒度納米TiO2更容易摻雜到纖維素間隙中，納米TiO2填補原有的自由體積空隙，從而減小復合體系的自由體積，進而減弱纖維素分子的鏈運動. 同時纖維素體系中摻雜納米TiO2打破原有的氫鍵網絡，納米TiO2表面羥基易于纖維素的羥基之間形成氫鍵，新的氫鍵網絡使得整個復合體系結構更加緊密，納米TiO2通過羥基抑制纖維素的鏈運動，使得復合體系的結構更加穩定，納米TiO2摻雜纖維素的熱穩定性增強.

圖7為不同納米粒度TiO2摻雜纖維素在70℃時的均方位移(MSD). 如圖7所示，摻雜不同納米粒度TiO2使得纖維素的MSD值出現不同的跳變. 摻雜納米TiO2粒度為2 ?、3 ?、4 ?、5 ?、6 ?、7 ?時，復合體系的MSD分別為3 ?2、10 ?2、11 ?2、20 ?2、27 ?2、34 ?2左右. 由此可以得出，隨著納米TiO2粒度的增加，納米TiO2摻雜纖維素的MSD逐漸增大，則纖維素的鏈運動逐漸增加，復合體系的穩定性逐漸變差. 摻雜不同納米粒度TiO2使得復合體系表現出明顯的粒度效應，摻雜納米TiO2粒度越小，纖維素的鏈運動越弱，復合體系熱穩定性較好.

圖7 70 ℃時不同納米TiO2粒度的MSDFig.7 MSDs of different Nano-TiO2 sizes at 70 ℃

4.4 機理分析

為了便于解釋納米TiO2粒度摻雜纖維素的機理，本文引入納米TiO2粒度表面羥基占有率的概念，其公式：

(9)

式中，PTiO2為納米TiO2粒度表面羥基占有率，MOH表面羥基原子數，MTiO2團簇總原子數.

表2是不同納米TiO2粒度表面羥基占有率，通過表2可以看出納米TiO2粒度越小，納米TiO2表面羥基占有率越高，小納米粒度的TiO2表面羥基與纖維素間形成的氫鍵數目占總體系氫鍵數目比重較大，納米TiO2抑制纖維素鏈運動的強度越大，使得復合體系更加穩定. 從不同納米粒度的納米TiO2摻雜纖維素的復合體系的自由體積和表面羥基占有率可以看出，當摻雜比例相同的情況下，納米TiO2摻雜纖維素表現出明顯的粒度效應，納米粒度越小，納米TiO2摻雜纖維素的復合體系更加穩定，復合體系的熱穩定性更強.

5 結 論

本文通過分子模擬對不同納米TiO2粒度摻雜纖維素進行模擬研究. 通過模擬結果和數據對比分析，得出以下結論：

表2 不同納米TiO2粒度表面羥基占有率

Table 2 Hydroxyl shares of different Nano-TiO2particle size surfaces

納米半徑(R)表面處理的TiO2團簇原子數(含氫原子)表面羥基占有率2.0?M(H/O/Ti)=6/6/10.463.0?M(H/O/Ti)=6/9/30.3304.0?M(H/O/Ti)=8/17/70.2505.0?M(H/O/Ti)=12/34/180.1886.0?M(H/O/Ti)=20/63/250.1857.0?M(H/O/Ti)=26/92/380.167

1)摻雜納米TiO2使得纖維素強度有較好提升，拉伸模量增大，抗形變能力增強，體積模量與剪切模量比值增大，韌性增強；摻雜納米TiO2使得纖維素穩定性提升，納米TiO2與纖維素形成的氫鍵抑制纖維素鏈運動，使得復合體系的結構穩定、熱穩定性增強.

2)隨著納米TiO2粒度逐漸減小，拉伸模量和柯西壓呈增大趨勢，泊松比逐漸減小，纖維素的強度增大；納米TiO2的粒度越小，納米TiO2表面羥基占有率越高，復合體系的自由體積越小，均方位移越小，纖維素鏈運動越弱，復合體系越穩定，納米TiO2摻雜纖維素熱穩定性越強，故摻雜小納米粒度TiO2是提升絕緣紙強度和熱穩定有效的方法.