高速鐵路主跨420m鋼箱拱橋設計方案研究

馮亞成

（中鐵第一勘察設計院集團有限公司，陜西西安 710043）

1 工程概況

西安至十堰鐵路位于陜西省東南部和湖北省西北部，線路西起陜西省西安市，向東南引線穿越秦嶺山脈，經商洛和十堰兩市，與建設中的武漢至十堰鐵路相接，正線全長252.855 km［1］。

橋位河段所處的漢江丹江口至遼瓦段為水庫常年回水區，根據航道規劃、河道自然條件以及船型發展趨勢，確定橋位河段采用天然Ⅲ級航道尺度。橋區水位受丹江口水庫調度影響，擬建橋位的設計最高通航水位采用丹江口樞紐正常蓄水位168.3 m，橋位處的設計最低通航水位取143.37 m，設計最高通航水位下推薦橋位斷面水域寬度為395 m。根據通航論證單位的評價意見，由于橋址處于彎道區，橋梁應一跨過河，其通航凈寬不得小于395 m［2］。

鉆孔資料揭示，橋址區兩岸基巖裸露，其中小里程側岸邊橋墩涉及地層主要為晉寧期輝綠巖，大里程側涉及地層為中元古界武當山群第二巖組片巖夾變粒巖；根據現有鉆孔的巖石試驗，片巖的單軸抗壓強度約為40 MPa 左右。橋址處工程地質條件較好。地震基本烈度為Ⅶ度，斷裂構造不發育。

2 主要設計標準

鐵路等級：高速鐵路。

正線數目：雙線。

速度目標值：250 km/h，有砟軌道，預留350 km/h。

正線線間距：5.0 m。

洪水頻率：設計1/100，校核1/300。

設計活載：ZK活載。

設防烈度：基本烈度為Ⅶ度，地震動峰值加速度為0.1g，地震動反射譜特征周期為0.35 s。

3 總體設計

根據防洪、通航部門的意見和地形條件，采用1孔420 m 的中承式鋼箱拱橋一跨跨越漢江的設計方案，左右兩岸主墩均位于設計最高通航水位邊線以外，通航凈高27.48 m，滿足凈高不低于10 m的要求。

鋼箱拱橋與鋼桁拱橋及鋼管拱橋相比，結構外形簡潔流暢，氣勢雄宏，景觀效果好；傳力路徑更加明確，設計、施工細節減少，有利于大節段運輸，施工速度快，質量更加有保障［3］。橋址附近漢江水域為湖北丹江口庫區省級濕地自然保護區的實驗區，對橋梁景觀要求較高，鋼箱拱橋能夠較好地適應地形和周圍環境。因此設計中對鋼箱拱橋方案作了重點研究。

主橋總體設計為主跨420 m 中承式鋼箱提籃拱橋，矢高105 m，矢跨比1/4，橋面距拱頂80 m，拱肋內傾4.5°。拱肋采用陀螺形鋼箱變高截面，拱腳截面高14 m，拱頂截面高8 m，箱寬4.5 m，板厚20～40 mm。拱腳橫向間距30 m，拱頂橫向間距13.5 m。吊桿采用低應力高強鋼絲柔性吊桿，間距12 m，全橋共設30對吊桿。主梁為1聯3跨的鋼箱梁，箱高3.0 m，寬17 m，孔跨布置為（46+384+44）m。拱肋鋼材材料為Q345qD鋼，拱橋基礎采用分離式明挖基礎。全橋立面布置見圖1。

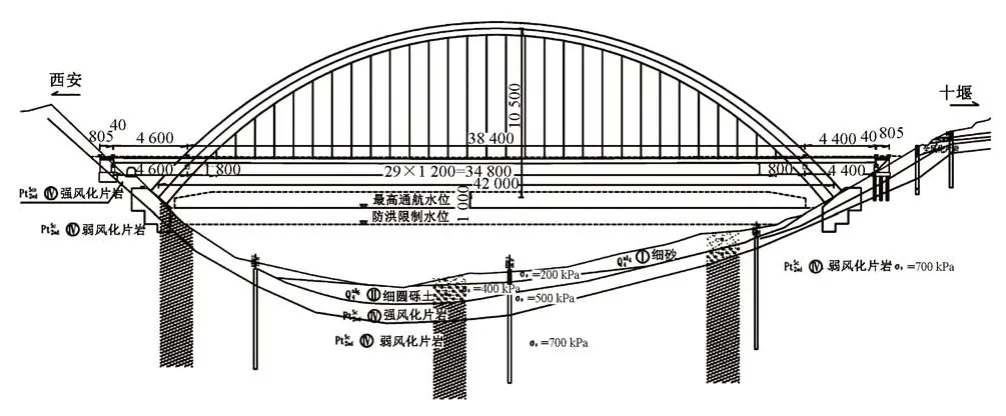
圖1 西十高速鐵路漢江特大橋鋼箱拱橋方案立面布置（單位：cm）

4 主橋結構形式研究

4.1 矢跨比

拱橋矢高對結構的受力合理性、吊桿長度、橫豎向剛度均有較大影響。我國鐵路拱橋的矢跨比一般在1/7～1/3。采用平面模型計算分析了1/6，1/5，1/4，1/3矢跨比時結構的受力。主力作用下不同矢跨比對拱腳荷載的影響見圖2。

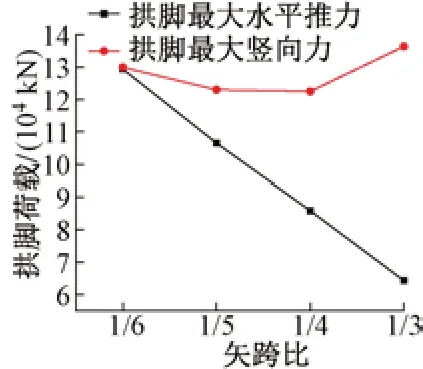
圖2 主力作用下不同矢跨比對拱腳荷載的影響

由圖2可知：①主力作用下拱腳最大水平推力隨著矢跨比的增大基本呈線性減小趨勢，矢跨比從1/6增大到1/3 時，最大水平推力由129 350 kN 減小至64 340 kN，水平推力減小50%；②主力作用下拱腳最大豎向力隨著矢跨比的增大呈先減小后增大的趨勢，相比矢跨比對拱腳水平推力的影響，矢跨比對豎向力的影響較小，不超過6%，且矢跨比為1/4 時豎向力最小，其值為122 510 kN。

進一步分析計算結果可知：①隨著矢跨比的增大，拱肋在恒載和活載作用下軸力均呈減小趨勢，且恒載減小的速率明顯大于活載；②活載產生的拱肋軸力約為恒載的17%，說明大跨度鐵路鋼箱拱橋拱肋軸力的構成中，恒載產生的軸力占主要成分。

不同矢跨比下拱肋彎矩見圖3。可知：矢跨比為1/3 時，拱肋在恒載、活載、整體升溫30 ℃及主力作用下的彎矩均最小；除恒載作用下，隨著矢跨比的增大，彎矩呈減小趨勢，尤其當矢跨比由1/6 變化到1/5 時，彎矩減小速率最快。可見，對于控制拱肋最大彎矩而言，應選擇較大的矢跨比。

計算時發現，隨著矢跨比的減小，結構的1階橫向和豎向振動周期均呈減小的趨勢，即隨著矢跨比的減小，結構剛度呈增大趨勢，并且鋼箱拱的橫向剛度明顯弱于豎向剛度。矢跨比為1/3 時結構剛度最弱。這是采用大矢跨比時結構重心上移的緣故。

隨著矢跨比的增大，總用鋼量呈先減小后增大的趨勢，矢跨比為1/4時總用鋼量最小。綜合考慮4種矢跨比結構的受力行為、美觀性及經濟性，矢跨比為1/4時鋼箱拱結構的拱肋彎矩、軸力均較小，拱腳水平推力最小，總用鋼量最省，因此本橋決定采用1/4的矢跨比。

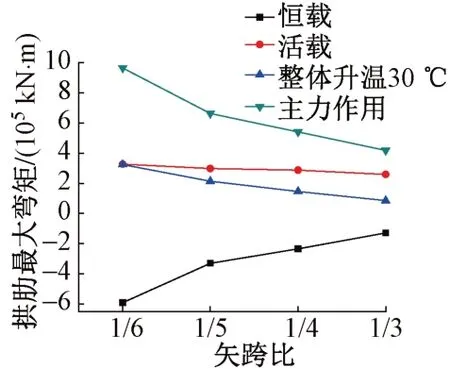
圖3 不同矢跨比下拱肋彎矩

4.2 拱軸系數

矢跨比確定后，懸鏈線的形狀由拱軸系數m［4］決定，即拱軸系數越大曲線在拱腳處越陡，曲線的四分點位越高。當m=1時，曲線為二次拋物線。

恒載作用下不同拱軸系數對主拱肋拱腳、1/4 拱肋處及拱頂截面彎矩的影響見圖4。

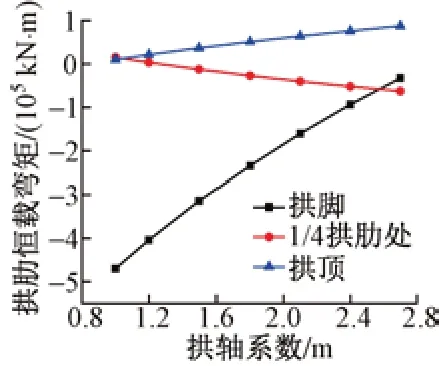
圖4 恒載作用下不同拱軸系數對主拱肋彎矩的影響

由圖4可知，拱軸系數對拱肋截面彎矩影響很大：①拱腳截面始終受負彎矩作用，負彎矩隨拱軸系數的增大而減小；②1/4 拱肋處恒載彎矩隨拱軸系數的增大由正變負且逐漸增加，當m接近2.57時其與拱腳截面彎矩相當；③拱頂承受正彎矩，隨拱軸系數的增大而增大。其中，拱腳彎矩對拱軸系數的變化最敏感。

活載作用下不同拱軸系數對主拱肋拱腳、1/4 拱肋處及拱頂截面彎矩的影響見圖5。

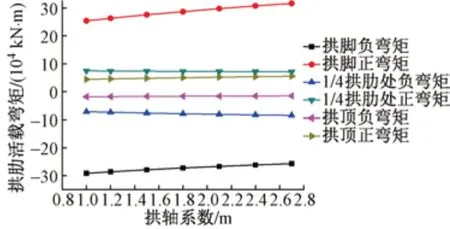
圖5 活載作用下不同拱軸系數對主拱肋彎矩的影響

由圖5可知：①隨著拱軸系數的增大，拱腳負彎矩減小了12%，正彎矩增大了25%。與其他截面相比，拱腳彎矩變化最大（圖5中最高線和最低線）。②當m從1.0變化到2.7時，1/4拱肋活載負彎矩由-72 410 kN·m增大到-85 733 kN·m，增大了18%，而1/4 拱肋處正彎矩隨拱軸系數的增大呈減小趨勢，但變化不大，減小了5%。③拱頂負彎矩隨拱軸系數的增大呈減小趨勢，減小了15%，正彎矩呈增大趨勢，增大了26%。此外，拱腳和拱頂截面的負彎矩隨拱軸系數增大而減小，正彎矩隨拱軸系數增大而增大；而1/4 拱肋處正、負彎矩的變化趨勢與此相反。計算分析表明，拱軸系數對恒載、活載作用下拱肋軸力的影響很小，最大值為5.5%，基本可以忽略。

主力作用下不同拱軸系數對主拱肋拱腳、1/4 拱肋處及拱頂截面彎矩的影響見圖6。

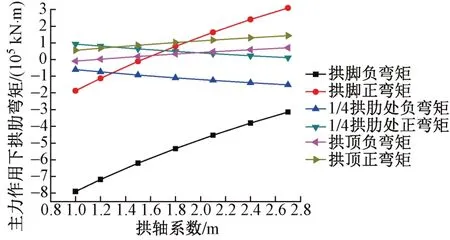
圖6 主力作用下不同拱軸系數對主拱肋彎矩的影響

由圖6可知：①隨著拱軸系數的增大，拱腳負彎矩逐漸減小，正彎矩逐漸增大；②拱頂彎矩隨拱軸系數的增大而增大；③1/4 拱肋處負彎矩隨拱軸系數的增大而增大，正彎矩隨拱軸系數的增大而減小。

綜上分析可知，增大拱軸系數可以有效減小拱腳負彎矩，但會增加1/4 拱肋處與拱頂截面彎矩。因此，拱肋采用全鋼結構時，拱軸系數取2.1較為合理。

4.3 拱肋內傾角

拱肋向橋軸線方向傾斜形成空間拱式結構，成為提籃拱。一般認為，提籃拱不僅提供了良好的橫向穩定性，也提供了一個較佳的建筑造型。從目前的研究結果和國內的工程實踐來看，拱的內傾角一般選擇3°～10°［5-7］。

大跨度拱橋的面外穩定性是工程中需要特別注意的問題。計算分析表明，主跨420 m 鋼箱拱橋結構的1 階屈曲模態為拱的面外非對稱彎曲，因此重點分析了內傾角變化時對結構橫向穩定系數的影響，見圖7。可知，增大拱肋內傾角可以顯著增大結構的橫向穩定系數。

橋面寬度一定時，拱腳的間距隨內傾角的增大而增大，而拱肋內傾角增大會直接影響下部的工程數量并給施工帶來困難。此外，拱肋內傾角的增大還會引起拱肋承載力的降低。因此，拱肋內傾角并不是越大越好。結合目前橋面采用的寬度，拱肋內傾角取4.5°。

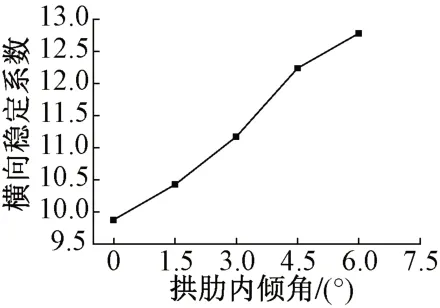
圖7 拱肋內傾角對結構橫向穩定系數的影響

4.4 橫撐數量

研究表明，拱肋之間設置橫撐可以有效增加結構的整體橫向剛度，提高結構面外剛度，從而提高拱橋的面外穩定性［8-9］。然而，橫撐并不是設置得越多越好，橫撐的設置與建筑造型的美觀性有關，并且可能影響結構的抗震性能。

對橋面以上橫撐的位置和數量進行比選。設計了0，3，5，7，9，11，14，15 道共8 種橫撐布置方案。限于篇幅，橫撐的位置示意圖未附。

4.4.1 橫撐對結構自振特性的影響

未設置橫撐時（0 道橫撐）結構1 階橫向自振周期為6.656 s，結構表現為拱肋向外對稱彎曲；當設置3道橫撐時，結構剛度明顯增加，周期減小，結構1 階橫向自振周期為3.889 s，減小了42%；當設置15 道時，1階橫向自振周期變化不再明顯，即由3 道橫撐增加到15 道橫撐時，變化不到10%。說明橫撐對于提高結構橫向剛度作用明顯，但當橫撐數量增加到一定程度時，結構1階橫向自振周期將不會產生顯著變化。

4.4.2 橫撐對穩定性的影響

設置橫撐可以極大地提高鋼箱拱橋的面外線彈性穩定系數。當設置3 道橫撐時，穩定系數比未設置橫撐時提高93%。當橫撐數量超過7 道時，面外穩定系數出現較大幅度增加；當橫撐數量超過11 道時，面外穩定系數又出現大的跳躍；當設置15 道橫撐時，穩定系數增大至12.647。

綜合考慮橫撐布置對結構自振特性和穩定的影響，以及全橋的整體美觀性，決定橋面以上橫撐布置采用9道橫撐的布置方案。

4.5 結構形式優化

主跨420 m 中承式鋼箱拱橋，初步計算結果顯示各項受力指標良好，但全橋用鋼量較大，每延米拱肋用鋼量為35.5 t，經濟性欠佳。為降低造價，提高方案的經濟性能，對拱肋的用鋼量進行了優化。

4.5.1 拱腳混凝土段長度的選取

為節省鋼拱肋的用鋼量，提高結構經濟性，對拱腳混凝土段長度進行了比選。分別設計了拱腳混凝土段長度為 0，12.2，24.0，36.7，51.1 m 這 5 種方案。拱腳不同混凝土段長度下結構受力對比見表1。

表1 拱腳不同混凝土段長度下結構受力對比

由表1可知，隨著拱腳混凝土段長度的增加，拱腳部位在恒載下的彎矩（簡稱恒載彎矩）和主力+附加力作用下的最大彎矩（簡稱最大彎矩）均增加較快。當拱腳混凝土段長度由0 增加到51.1 m 時，拱腳最大彎矩由 424 963 kN·m 增加到 1 260 424 kN·m，增大了196%，用鋼量由14 907.1 t 減小到11 140.2 t，減少了25.3%。當拱腳混凝土段長度為51.1 m 時，拱腳最大彎矩過大，拱腳截面受力無法滿足要求。結合拱腳的受力、拱肋節段劃分及混凝土段的施工可行性，拱肋混凝土段長度不宜過長。綜合分析，混凝土段的長度為37 m 左右時，既可以保障結構受力，又可以降低工程造價。

4.5.2 拱軸系數的優化

拱軸系數對拱腳恒載彎矩影響較大。當拱腳采用混凝土截面時，與全鋼結構相比，拱肋恒載內力分布差異較大。因此，考慮改變拱軸系數減小恒載彎矩，從而改善拱腳部分的受力。

計算結果表明，拱肋鋼箱部分應力不控制設計，結構剛度控制設計。對鋼箱截面的板厚、拱腳段混凝土截面的尺寸進行了優化。分別取m=2.1，2.4，2.7，3.0，3.3，3.6 進行方案設計。拱腳混凝土段長度統一取37 m。不同拱軸系數下拱腳彎矩見圖8。

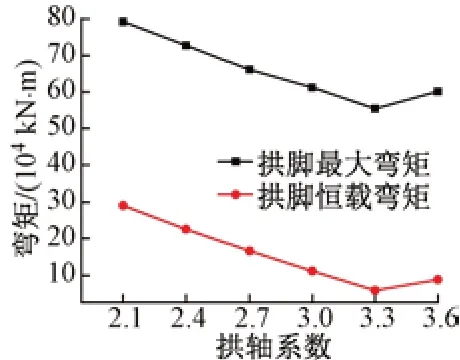
圖8 不同拱軸系數下拱腳彎矩

由圖8可知：當m=2.1～3.6時，拱腳恒載彎矩和拱腳最大彎矩均隨拱軸系數的增大呈先減小后增大的趨勢；當m=3.3時，拱腳恒載彎矩最小，其值為554 011 kN·m。

不同拱軸系數下拱頂彎矩見圖9。可知：拱頂彎矩隨拱軸系數的增大而增大。m由2.1增大到3.6時，拱頂恒載彎矩增大至87 570 kN·m，增大了93%，拱頂最大彎矩增大至180 002 kN·m，增大了36%。可知，當m=2.1～3.6時，拱頂截面彎矩不控制設計。

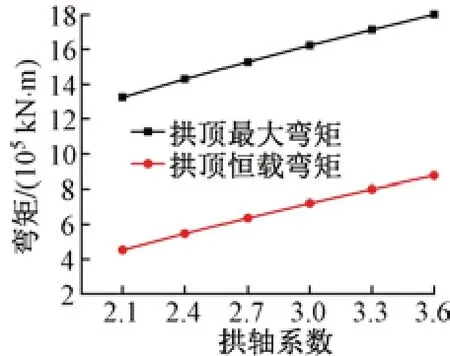
圖9 不同拱軸系數下拱頂彎矩

考慮拱腳為混凝土結構，且拱肋承受較大的彎矩，為改善其受力，拱軸系數取3.3時結構受力較為合理。通過一系列的優化設計，拱肋的每米用鋼量由35.5 t/m降低到22.6 t/m，極大提高了鋼箱拱橋的經濟性能。

5 結構計算分析結果

1）靜力計算結果

優化后結構的靜力計算結果見表2。可知，主跨420 m中承式鋼箱拱橋的各項指標均滿足規范要求。

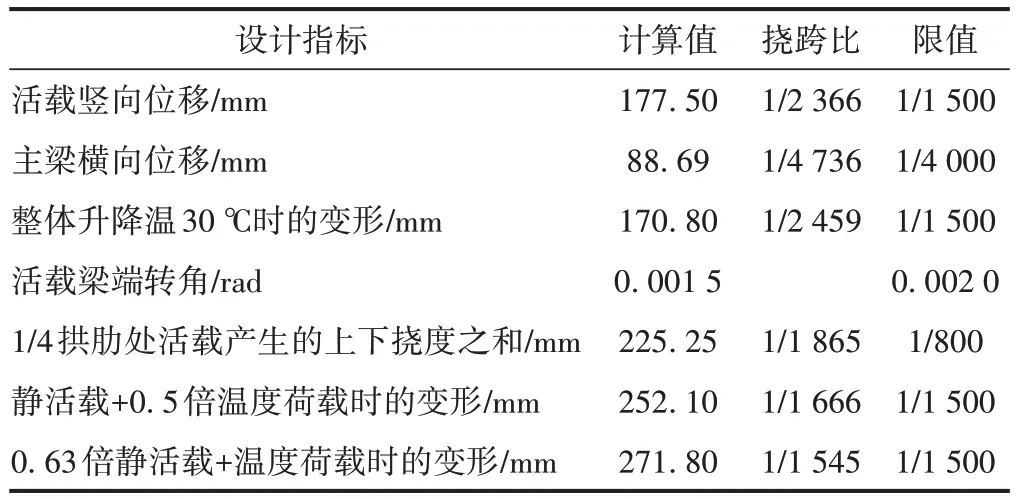
表2 主跨420 m大跨鋼箱拱橋靜力計算結果

2）動力計算結果

主跨420 m 鋼箱拱橋自振特性見表3。可知，前5階振型中，有4階為橫向彎曲振動，說明大跨鋼箱拱橋橫向剛度比其他2個方向偏弱。

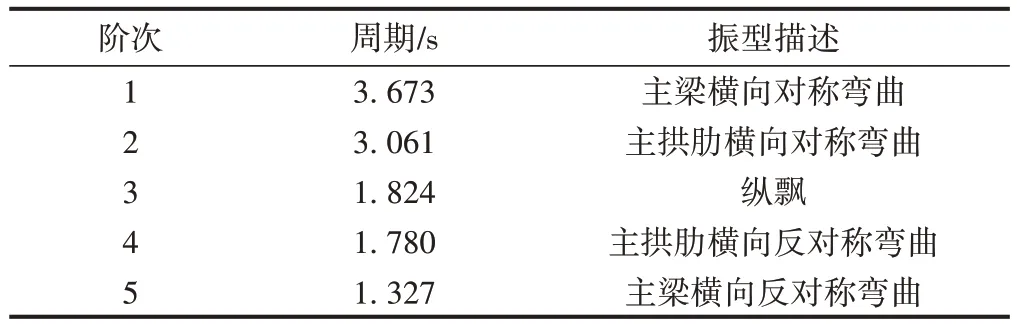
表3 主跨420 m鋼箱拱橋自振特性

3）車橋耦合動力仿真分析結果

根據車橋耦合動力仿真分析結果可知，在國產CRH3動力分散式車組以180～420 km/h 運行時，橋梁的振動性能良好，動車與拖車的脫軌系數、輪重減載率、輪軌橫向力等安全性指標均在限值以內，豎向和橫向舒適性均達到“優”。

6 施工方案

大跨度鋼拱橋的施工方法較多，常采用的有滿堂支架法、拱肋邊拱支架+中拱整體提升法、轉體施工法、斜拉扣掛施工法等。考慮到本橋位于水庫常年回水區，轉體施工及斜拉扣掛均能完成施工。對2 種施工方法進行綜合分析，轉體施工法大部分焊接可在地面完成，質量有保證，但由于拱腳段采用混凝土，轉體重量大，球鉸設計難度大，施工風險高；斜拉扣掛法施工工藝成熟，施工風險小，缺點是拱肋高空焊接工作量較大，因此本橋推薦采用“纜索吊機+斜拉扣掛法”施工方案［10］，兩岸拱座上各設置1 座扣塔，主拱合龍前，拱肋荷載通過扣索由扣塔承受。

拱腳安裝定位完成后，主拱肋開始2 個節段利用浮吊安裝，其余節段采用纜索吊機施工，兩岸主拱肋橫梁至橋臺范圍內的主梁采用纜索吊機先水上整體提升，再在支架上縱向滑移完成，主拱肋橫梁之間的主梁和所有吊桿采用纜索吊機直接架設完成。成拱后安裝吊桿、鋼箱梁及橋面系。

7 結論

1）大跨鋼箱拱橋通過合理的參數設計，可以滿足高速鐵路的行車要求。

2）大跨鋼箱拱橋在拱腳段設置合理長度的混凝土段，不僅可以提高結構的剛度，而且能大幅度提高其經濟性能，提高大跨度鋼箱拱橋的競爭力。

3）車橋耦合動力仿真分析結果表明，橋梁的振動性能良好，具有足夠的豎向和橫向剛度，能夠滿足高速鐵路以350 km/h 運行時的安全性和舒適性要求。