基于APOS理論視角下的數學定理教學

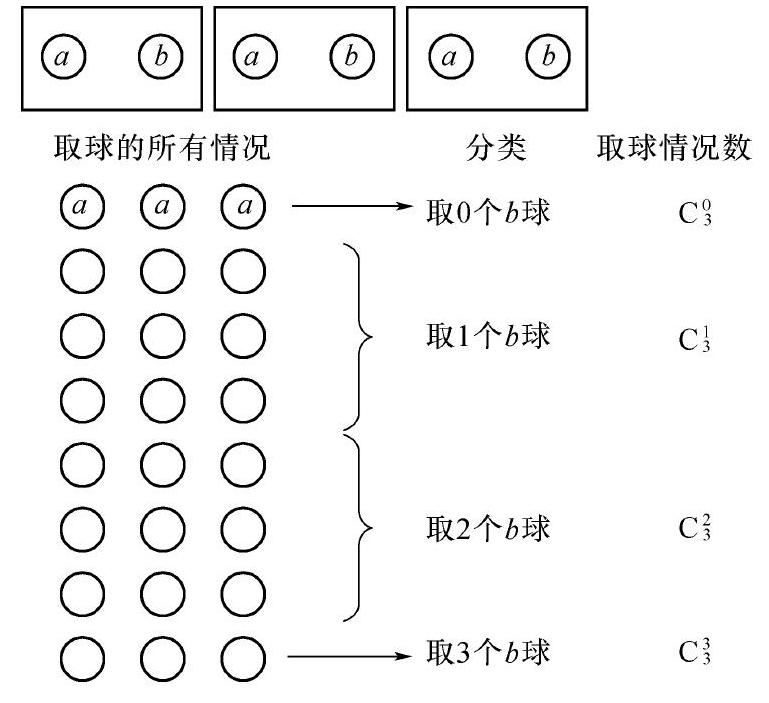
摘 要：二項式定理是高中數學定理的重要組成部分，是初中多項式乘法的延伸，對于培養學生的數學抽象等核心素養有著不可忽視的價值。本文將運用APOS理論對其教學過程進行分析和設計。

關鍵詞：APOS理論;數學定理;二項式定理

數學知識具有很強的抽象性，在教學當中應注重體現知識的來龍去脈，經歷數學知識由具體到抽象的過程。但很多教師對于定理教學的把握不到位，導致學生對于定理的形成過程一知半解，死記硬背，不利于數學知識的理解和數學能力的培養。二項式定理是人教版高中數學選修3-2第一章第三節第一課時的內容，是代數多項式乘法的推廣。它是安排在計數原理之后的內容，既是對計數原理的應用，同時也為后面學習隨機變量及其分布、二項分布等內容做鋪墊。接下來筆者將結合APOS理論對二項式定理的教學過程進行分析和設計。

一、 APOS理論概述

APOS理論是20世紀80年代由美國數學教育家杜賓斯基在皮亞杰反思性抽象理論的基礎上提出的有關數學學習的理論。該理論認為學生學習數學知識需要經歷四個階段的心理建構，即活動階段（Action）、過程階段（Process）、對象階段（Object）和圖式階段（Scheme）。APOS理論是以建構主義為基礎的數學學習理論，核心是引導學生通過心理建構，掌握數學知識。“活動”是指個體對感知到的數學對象進行各種變換。這里的“活動”泛指所有的數學活動，不僅僅指個體的肢體動作，還包括回憶、推理等。當個體重復“活動”或“動作”并對其進行反思時，“活動”就會被內化進入心理“過程”，“過程”的一個重要特征是個體能夠完全在他的思想中描述或反思轉換的步驟而不實際進行操作。當個體把“過程”作為一個整體并且對整體實施新的動作時，該“過程”被壓縮到一個心理“對象”中，這時個體不再關注動態的“過程”，而是靜態的“對象”本身。“圖式”被定義為個體的“活動”“過程”“對象”和其他圖式的整合。“圖式”的建立是一個長期的過程，這些圖式在個體頭腦的連貫框架中有意識或無意識的聯系在一起，用來解決和他們相關的問題。本文將從APOS理論的視角對“二項式定理”的教學做一個分析和探討。

二、 APOS理論視角下的二項式定理教學

依據APOS理論，筆者認為學生對于二項式定理的認識也需要經歷以下四個階段。

第一階段：活動階段（Action）

活動是學生掌握二項式定理的一個必要條件，我們不能馬虎。數學教學活動應建立在學生已有的認知發展水平和知識經驗的基礎上。在教學過程中不僅需要外在的動作，如操作、實驗等，也需要內在的思維活動，如回憶、思考等。

設計意圖：利用二項展開式的通項求解相關問題，深化學生對于二項式定理的理解。

第四階段：圖示階段（Scheme）

在這一階段將學習的二項式定理進行總結，建立與其他概念、定理、定義之間的聯系，形成綜合的心理圖示。

（四） 課堂總結

本節課主要學習了哪些內容？運用了哪些數學思想方法？

設計意圖：引導學生對本節課學習的知識進行總結，使學生對于二項式定理有一個清晰全面的理解，建立起二項式定理與其他相關概念的聯系。

APOS理論揭示了學生學習數學知識的全過程，四個階段的教學使學生深化了對二項式定理的理解，實現了真正意義上的建構，取得了較好的教學效果。但運用APOS理論指導教學時需注意，有時對于數學知識的理解并不嚴格遵循四個階段的這種線性途徑，如程序和對象階段也會有活動的影子，所以四個階段之間還會存在一種循環。

參考文獻：

[1]管尤躍.基于APOS理論下的小學數學概念教學模式——以《三角形的認識》為例[J].小學教學研究，2017（7）：8-11.

[2]趙紅霞，李丹.基于APOS理論的小學數學概念教學研究——以《軸對稱圖形》教學為例[J].兵團教育學院學報，2018，28（2）：61-65.

作者簡介：顧慶梅，山東省青島市，青島大學。