基于灰色GM(1,1)改進模型的年度風功率預測

(華電電力科學研究院有限公司，杭州 310030)

0 引 言

年度風功率具有預測期間長，影響因素眾多的特點，采用數理統計方法預測精度較低。灰色預測模型GM(1,1)所需要的負荷數據較少，而且不用考慮其分布規律，可應用于年度風功率預測。

但GM(1,1)模型也存在一些不足之處。一是原始數據灰度越大，預測精度越差；二是不適合于長期后推若干年的預測，有意義的僅僅是前一兩個預測數據[1]。為此，文中從兩個方面對GM(1,1)模型進行改進，一是對累加生成數列進行平移變換，二是對GM(1,1)模型中的背景值構造公式進行改進。并應用該改進模型對某風電場測風塔年平均風速進行預測，結果表明改進模型的預測精度有一定提高。

1 GM(1,1)的建模過程

GM(1,1)模型是應用非常廣泛的一種灰色模型，它的建立只需要一個數列。具體步驟如下：

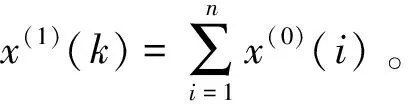
(1)

式中，a為發展系數，反應x(0)序列的增長速度，x(1)(k)為背景值。將式(1)以離散形式表示，并采用最小二乘法，可以得到a和u的估計值。

(2)

其中:

Y=[x(0)(2),x(0)(3),…,x(0)(n)]T

(3)

(4)

a和u的估計值確定后，可以確定微分方程式(1)，解微分方程并對其進行累減還原，得到x(0)預測方程：

k=(0,1,2…)

(5)

2 對GM(1,1)模型的改進

2.1 對累加生成序列進行平移變換

原始數據的離散程度較大時，預測誤差比較大。針對這一問題，文中采用對累加生成序列進行平移變換的方法。將GM(1,1)模型中的背景值x(1)(k)換為x(1)(k)+w，然后建立優化模型，求得最佳的平移值w。

(k=2,3,…n)

(6)

從式(6)可以看出殘差和平移值w的數量關系，為了得到殘差值最小的平移值，建立如下目標函數：

(7)

通過對w求導并令其為0，可得最佳w值為：

(8)

2.2 改變微分方程的背景值構造公式

GM(1,1)模型的灰微分方程為：

x(0)(k)+az(1)(k)=u,k=2,3,…n

(9)

在原始模型中有：

z(1)(k+1)=0.5[x(1)(k)+x(1)(k+1)],

k=1,2,…n-1

(10)

式(10)是一個平滑公式，當時間間隔較短，原始數據變化幅度較小時，采用式(10)是合適的。然而，當原始數據變化幅度較大時，采用這樣的背景值公式會使得預測誤差很大。從z(1)(k)的幾何意義出發，文中構造如下公式：

(m-1)x(1)(k+1)],k=1,2,…n-1

(11)

(12)

(13)

將該模型稱之為GM(1,1,m)模型。

3 實例分析

選擇某風電場測風塔2007～2014年年均風速(單位：m/s)為原始數據序列，利用MATLAB建模，預測2015～2018年年均風速。文中對原始GM(1,1)模型做了兩項改進，為驗證各項改進的單項效果和綜合效果，做如下計算(2007～2014年原始數據及各序列擬合值見表1，各序列參數及后驗差檢驗見表2，2015～2018年預測值及誤差分析見表3)。

(1)令原始數據為序列0，不對其進行處理，采用原始GM(1,1)模型進行預測，得到數據序列1，并對其進行后驗差檢驗和誤差分析。

(2)利用公式(8)計算平移值，將累加生成序列平移變換，采用原始GM(1,1)模型進行預測，得到數據序列2，并對其進行后驗差檢驗和誤差分析。

(3)不對累加生成序列進行處理，采用GM(1,1,m)模型進行預測，得到數據序列3，并對其進行后驗差檢驗和誤差分析。

(4)對累加生成序列進行平移變換，同時采用GM(1,1,m)模型進行預測，得到數據序列4，并對其進行后驗差檢驗和誤差分析。

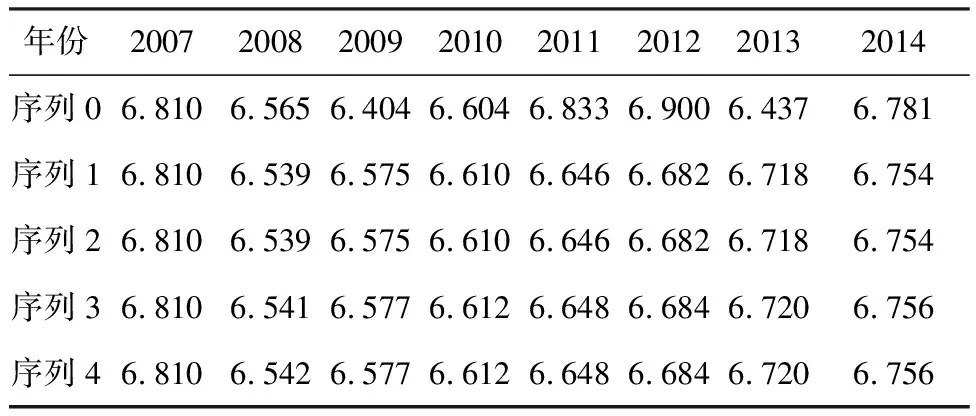
表1 2007～2014年各序列擬合值

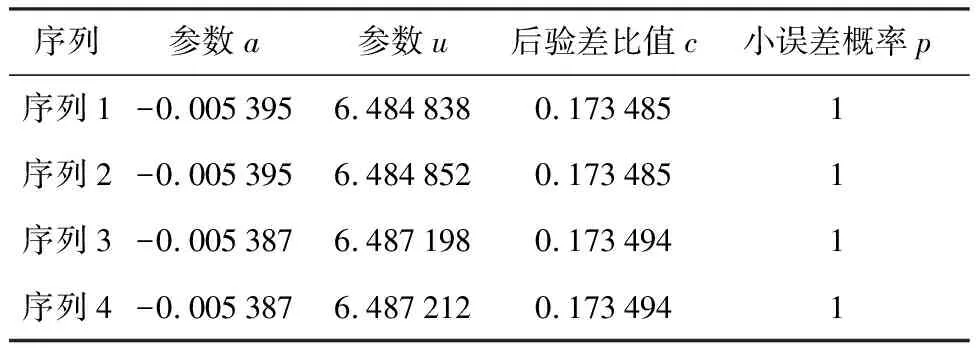
表2 各序列參數及后驗差檢驗

由表2可知，各序列后驗差比值均小于0.35，小誤差概率均大于0.95，預測精度全部為一級。

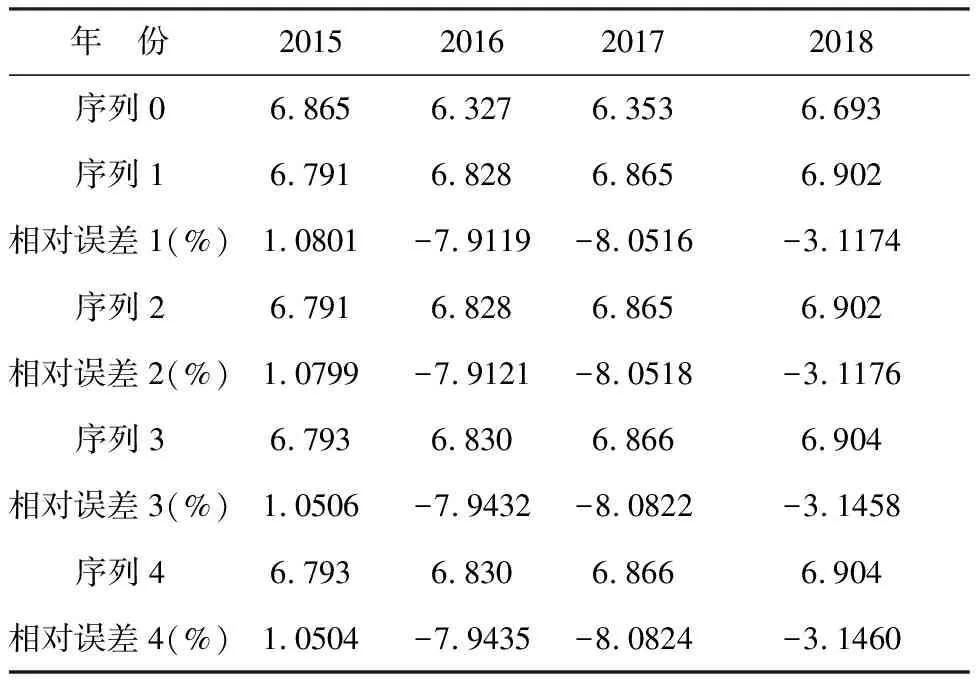
表3 2015至2018年各序列預測值及誤差分析

分析表3中2015年和2016年的預測值及相對誤差，將序列2、3、4和序列1對比可知，對累加生成序列進行平移變換和改進背景值構造公式，均可以提高預測精度，改進背景值構造公式對提高預測精度的貢獻更大一些。

分析2017年和2018年預測值及相對誤差可知，其預測精度變化不具有規律性。這也證明GM(1,1)不適合于長期后推若干年的預測，有意義的僅僅是前一兩個預測數據。

4 結束語

文中針對原始GM(1,1)模型的不足之處，從兩個方面對其進行改進：對累加生成序列進行平移變換，改善背景值構造公式。并應用改進模型對某風電場測風塔年均風速進行預測，預測結果表明其可行有效。