電除塵器內部流動特性的數值模擬

(河北工業大學能源與環境工程學院，天津 300401)

0 引 言

靜電除塵器(ESP)是一種從煙氣流場中高效去除微小顆粒的裝置[1]。ESP中粒子運動軌跡受到包括氣流流動阻力、粒子自身的重力、空氣中性粒子與帶電粒子發生能量交換產生的二次電流體動力學(EHD)流動等多方面因素的影響，這使得流場形態變得錯綜復雜[2]。

研究人員對ESP進行了大量的實驗和數值模擬的研究，Chun等人[3]使用SIMPLEST算法研究了線板ESP中k-?湍流模型的二維EHD流動模式。Farnoosh等人[4]使用FCT-FEM方法模擬電暈放電和標準k-?模型預測EHD流場中的三維EHD流模式。Feng等[5]采用混合方法FEM-FVM先是分析了電除塵器內部渦流特征對EHD流動的影響，隨后驗證了幾種典型的ESP中的EHD流動模型[6]。Shen等人[7]運用CFD技術模擬了幾種不同集電極下EHD流動模式。Mizeraczyk[8]通過二維PIV測量來研究各種粉塵濃度對多線ESP中EHD流動模式的影響。寧致遠[9]使用PIV測試了幾種不同的電極幾何形狀的粒子收集效率和EHD流速場等。

文中在前人研究的基礎上構建了一種三維線板式ESP模型，利用COMSOL軟件進行數值模擬，研究了靜電場中電暈電場和空間電荷密度的分布規律，且定量分析了主氣流與電暈放電產生的二次EHD流對流場特性、粒子運動軌跡和收集效率的影響，并將數值模擬結果與已有實驗進行了對比。

1 數學模型

1.1 靜電場模型

在電暈放電過程中，放點電極周圍空氣被電離荷電，形成薄薄的一層電離層，電離層產生的電荷在向收塵極板靠近的過程中形成空間電荷，其中電場由泊松方程表示：

▽2φ=q/ε0

(1)

E=-▽φ

(2)

其中，φ是標量電位,V；q表示空間電荷密度，C/m3；E為電場強度，V/m；?0為環境氣體介電常數，8.854e-12F/m。

空間電荷密度由電流連續性方程控制：

J=μEEq+uq-D▽q

(3)

▽J=0

(4)

式中，J為電流密度，A/m2;μE為離子的遷移率，2.2×10-4m2/(V·s);D為離子擴散系數，5.2×10-5m2/s;u表示流速，m/s。

1.2 氣流流動模型

湍流流場通過COMSOL軟件中k-ε湍流模型結合穩態不可壓縮Navier-Stokes方程共同求解。Navier-Stokes方程中的質量守恒方程和動量守恒方程求解流速u和壓力p，由下式給出：

(5)

▽(pu)=0

(6)

其中,u為速度場，m/s；p為壓力，pa；I為單位矩陣；F為附加電場力，N/m3；ρ為流體密度，kg/m3；k為湍流動能，m2/s2；μ為流體動力粘度，kg/m·s。

標準k-ε湍流模型由湍動能方程和耗散率方程組成，控制方程如下：

(7)

(8)

其中,ep為湍流耗散比,m2/s3；其余參數為湍流模型相關常數：Cg1=1.44，Cg1=1.92，Cμ=0.09，σk=1。

1.3 粒子荷電模型

在電場中，粒子荷電方式有兩種：一種粉塵荷電是使離子在電場力作用下與粒子碰撞實現荷電，稱為電場荷電；另一種是離子做擴散運動時碰撞粒子使其荷電，稱為擴散荷電。對于直徑大于1 μm的顆粒，電場荷電通常大于擴散荷電，文中僅考慮電場荷電。粒子荷電量與粒子直徑、電場強度等因素有關，粒子荷電方程由下式給出:

(9)

其中,qp為粒子荷電量，C；qs為飽和荷電量，C。

1.4 粒子運動模型

粒子進入流場后除了受到粒子自身的重力和流場相對運動阻力的影響之外，還會受到強大電場力的作用使粒子遷移到收集板上。粒子的運動軌跡由以下力平衡方程表示:

(10)

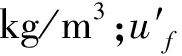
2 邊界條件

文章采用的是典型的線板式除塵器3D模型，模型由兩個平行收塵板組成流場通道，1個半徑為1 mm的電極位于流場中心位置，由圖1所示，流場通道長L為500 mm，兩個收塵板高H為100 mm、間距W為100 mm，X,Y,Z表示方向，主流空氣沿著Y軸正方向流動。

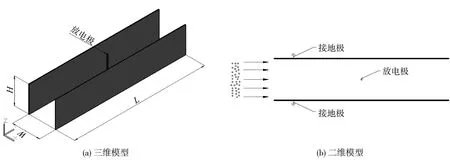
圖1 線-板式靜電除塵器數學模型

電除塵器內部邊界條件由表1給出，對于電暈放電過程，電暈電極給定直流電勢為30 kV，接地極為零，其他邊界為零通量。Katpzov假說[10]認為電場強度與起始電暈放電電壓以下的電壓成正比地增加，在電暈產生后它的值維持不變。由Peek公式[11]確定了電暈電極起暈電場強度：

(11)

其中,rc為電暈線半徑，單位為cm。

表1 數值模型邊界條件

3 數值結果

3.1 靜電場

圖2為46.2 kV施加電壓下xy平面(z=0)的電勢與空間電荷密度分布。電暈線表面電勢等值線密度很大，周圍分布呈圓形，隨著向通道邊緣的擴散，電勢逐漸減小，等值線分布呈橢圓形。空間電荷密度最大值位于電暈線表面附近，等值線分布呈圓形，當遠離線電極表面時，空間電荷密度迅速減小。對于電勢來說，由電暈電極中心位置向極板方向衰減速度大于進出口方向，而空間電荷密度向進出口方向衰減速度大于極板方向。

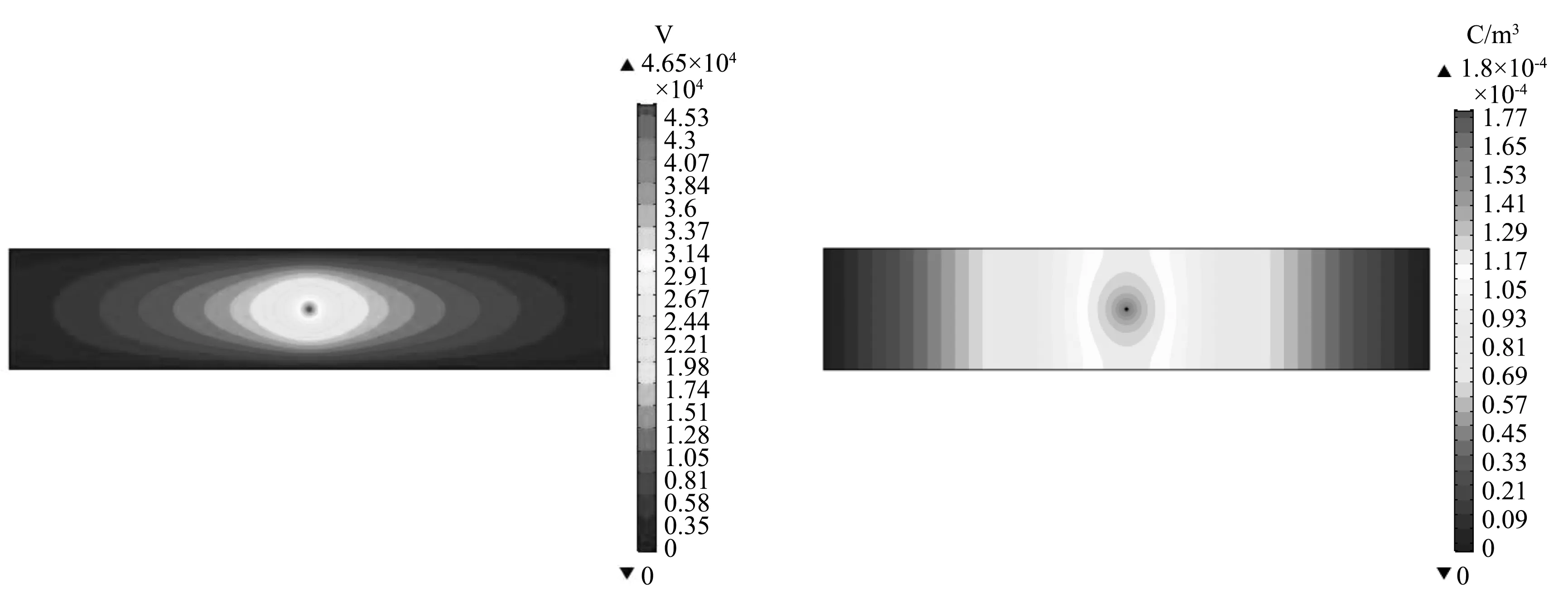
圖2 電除塵器內部電勢與空間電荷密度等值線分布圖

為了驗證數學模型，圖3示出了數值結果與Penny和Matick[12]在38.7、43.5、46.2 kV施加電壓下的電場分布實驗數據對比。由圖3可知在收塵板沿法線方向電勢模擬數據與實驗結果表現為相同的趨勢，數值模型可以有效模擬出電除塵器內部電勢分布。

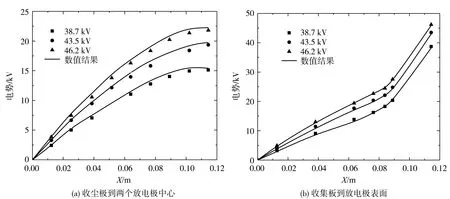
圖3 電勢模擬結果與實驗結果對比

3.2 氣體流場

對入口氣體流速分別為0、0.4 、0.5 、1 m/s時單線-板ESP內部流場進行數值模擬，結果圖4所示。在沒有任何主氣流的條件下，由于電流體力的作用，電暈電極表面周圍產生離子風，形成四個對稱的渦旋，二次EHD流主導整個流場。隨著初始速度的增加到0.4 m/s，二次EHD流受到主氣流速影響，上游區域和下游區域在主流方向上被拉伸，在收塵板附近形成兩個較為對稱的渦旋，當入口流速進一步增大到0.5 m/s時，渦旋消失，二次EHD流影響微乎其微。而1.0 m/s時由電暈放電引起的二次流動消失，主氣流主導了整個煙氣通道，圖4中的流線圖和參考文獻[13]中描述的數值結果趨勢一致。

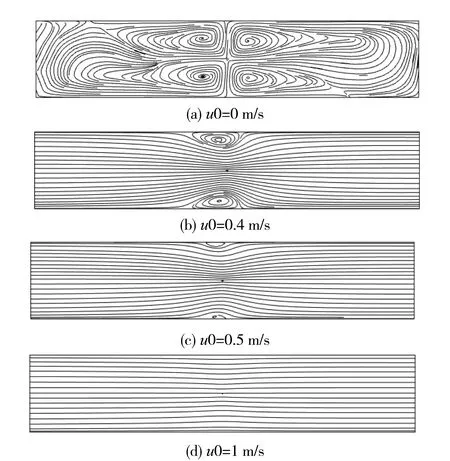
圖4 不同入口流速下XY平面(z=0)的二維流線圖

3.3 粒子運動

收集效率引用了kihm[14]的實驗數據進行驗證，構建了一種長寬高為 400 mm×50 mm×50 mm、極間距為50 mm的8電極靜電除塵器，在入口以 2 m/s的流速均勻釋放4 μm的顆粒。將數值計算結果與實驗結果進行對比，結果如圖5所示，數值計算與實驗結果相對誤差小于15%，足以證明數值模型的可行性。

對粒徑分別為1、2.5、5、10 μm的粒子進行粒子追蹤，在入口處分別釋放1000個粒子，對0.3～1 m/s主流速下的內部流場進行數值分析，結果見表2。隨著主流速由0.3 m/s提升至1 m/s，1 μm粒徑粒子的收集效率從48%下降到15%。當入口流速從0.3 m/s增加到0.5 m/s時，收集效率下降20.1%，而從0.8 m/s增加到1 m/s時，收集效率下降2.6個百分點。可以看出，在較小流

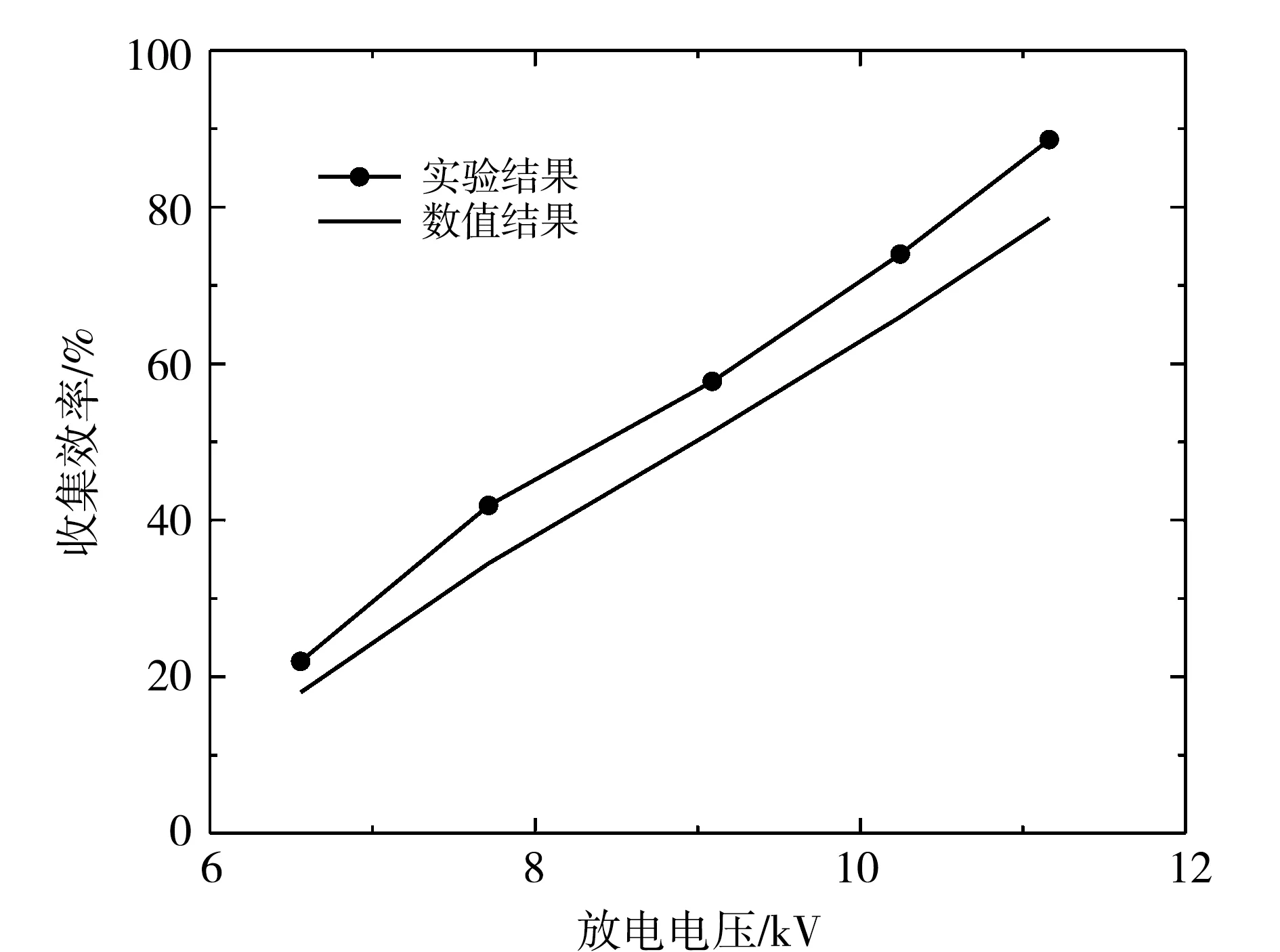
圖5 數值結果與實驗結果的收集效率對比

表2 不同入口流速下1 μm粒子收集效率比較

速段，主流速對于收集效率的影響較大，而從0.8 m/s開始，主流速對于收集效率的影響逐漸減小。除了主流速度以外，電暈電壓對于粒子收集效率也有較大影響。由表3給出，對于入口流速為1 m/s的粒子，收集效率從30 kV的15%提升到50 kV的22.3%。

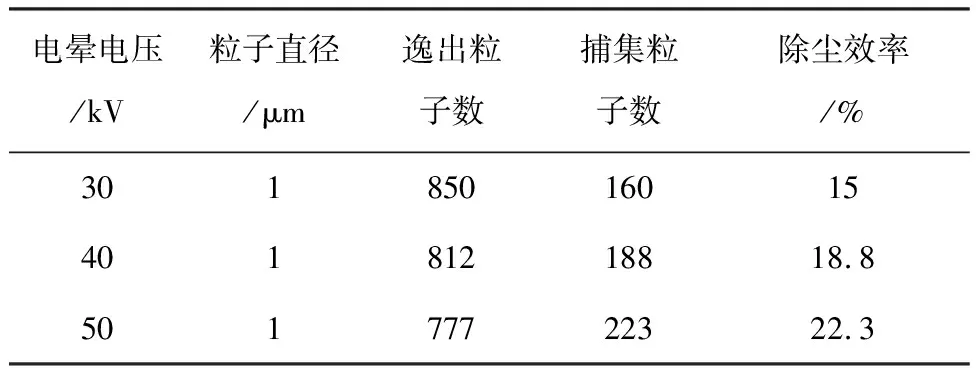
表3 不同電暈電壓下1 μm粒子收集效率比較

在入口處分別釋放1 000個粒子，其中1、2.5、5、10 μm各占25%，運動軌跡如圖6所示。對于1 μm粒徑的粒子，釋放的250個粒子中有212個粒子粘附在出口邊界上，收集效率只有15%，而對于2.5 μm和5 μm的粒子，收塵效率分別提高至34%和66.5%，而10 μm粒徑粒子在通過放電極附近位置時，完全被捕集在收塵板上。由此可知，隨著粒徑的增大，粒子荷電量逐漸增加，粒子更容易粘附在放電極對應區域的收塵板上。除此之外，可以看出隨著粒子直徑的增加，粒子經過線電極后粒子運動更加貼近收塵板，這說明主流速度的影響逐漸減小，EHD流影響增強。

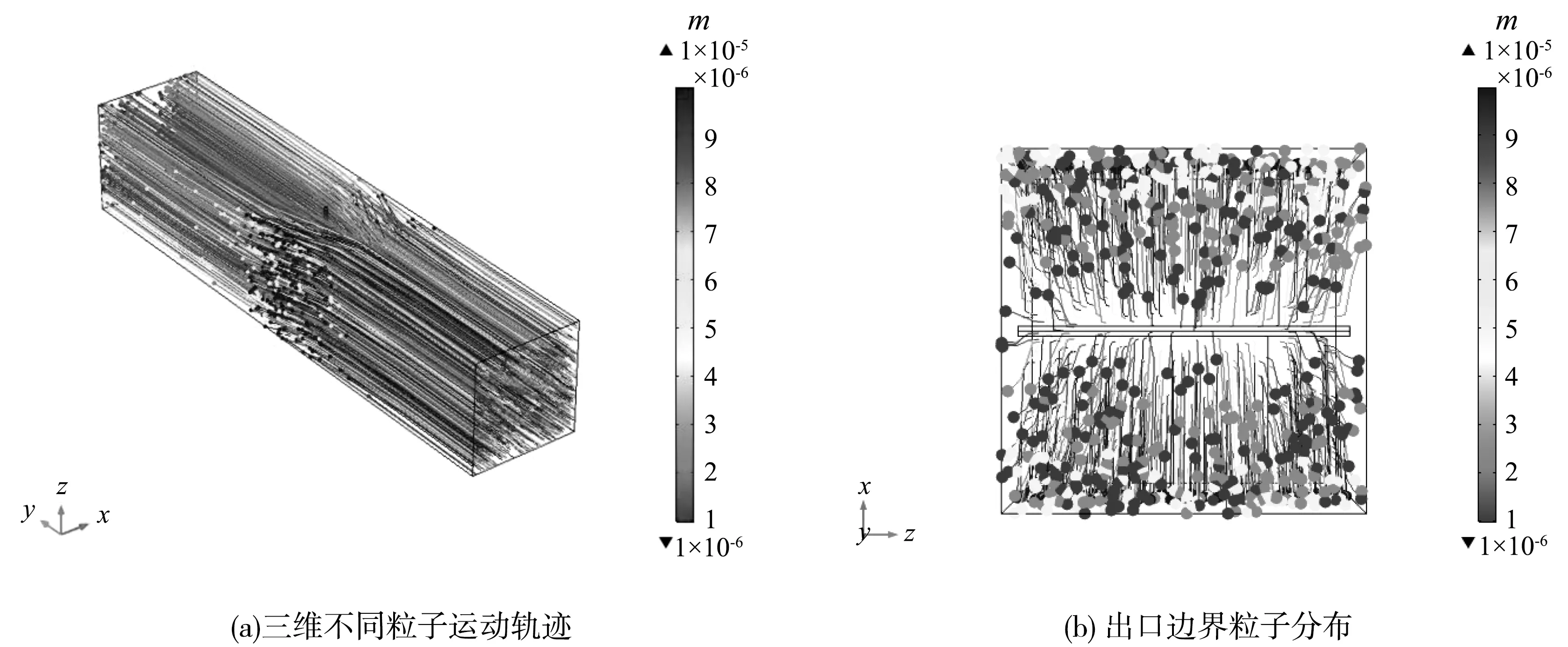
圖6 不同粒徑粒子運動軌跡圖

除了ESP內部流動之外，進一步定量分析了EHD流對于除塵效率的影響，結果見表4。有EHD流工況下粒子收集效率略高于無EHD工況下的收集效率，以粒子直徑1 μm，入口流速1 m/s為例，收集效率提升了1.2%。粒徑為2.5，5，10 μm的粒子分別在低于0.3、0.5、1 m/s的入口流速下收集效率不受EHD流的影響。綜上可知，EHD流僅對于微小粒子收集效率有略微的提高作用，對于整體收集效率的影響可以忽略不計。

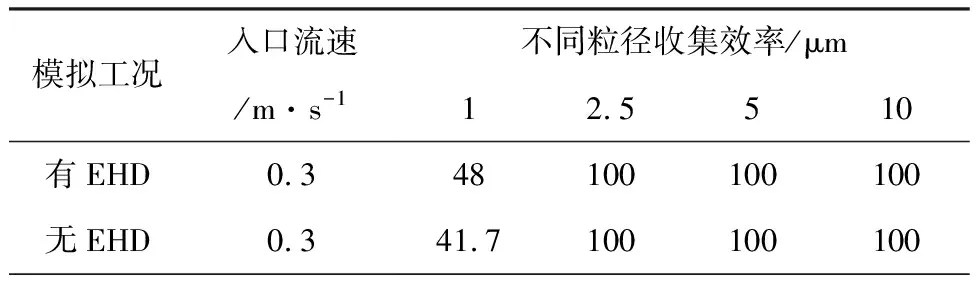
表4 各種粒徑粒子在有無EHD條件下的收集效率

續表4

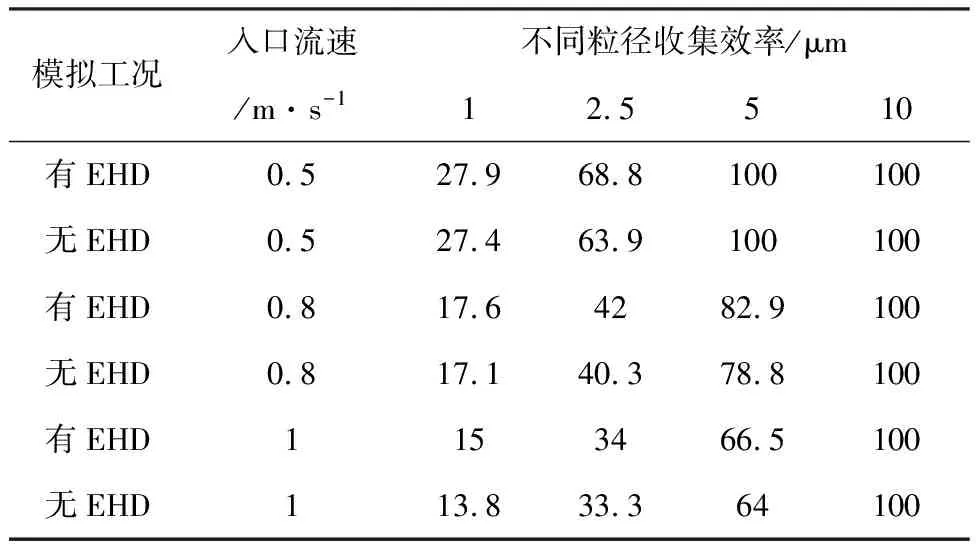
模擬工況入口流速/m·s-1不同粒徑收集效率/μm12.5510有EHD0.527.968.8100100無EHD0.527.463.9100100有EHD0.817.64282.9100無EHD0.817.140.378.8100有EHD1153466.5100無EHD113.833.364100

4 結束語

文中建立了一種三維線板式數值模型，對除塵器內部電暈放電，湍流流動，粒子運動軌跡和收集效率進行了分析，得到以下結論：

(1)隨著電暈電極中心位置向煙氣通道兩端擴散，電暈電場內部電勢和空間電荷密度都逐漸減小。不同的是，電勢在垂直極板方向的衰減速度較快，而空間電荷密度在進出口方向衰減速度較快。

(2)當煙道入口流速小于0.5 m/s時，由于EHD流的作用，氣流場會產生渦旋，在沒有來流速度的情況下，在煙道中心形成四個對稱的較大渦旋，隨著主流速度的增大，渦旋逐漸減小且向收集板靠近，當主流速度達到1 m/s時，EHD流影響消失。

(3)對于1到10 μm的粒子，隨著主流速度的增加，粒子收集效率逐漸降低，尤其是對于小粒徑粒子較為明顯。隨著電暈電壓的增大，粒子的收集效率增大且粒子直徑越大越容易被捕集，有無EHD流對于微小粒子的收集效率影響可忽略不計。

(4)將數值結果與已有實驗進行了對比，取得了良好的結果，驗證了數值模型的可靠性。