MUSIC算法性能研究綜述

田航

摘? 要：智能天線的核心技術之一是波達方向（Direction of Arrival，DOA）估計，其在無線通信中具有重要作用。多重信號分類（Multiple Signal Classification，MUSIC）算法是經典的DOA估計算法，但因其對于相干及小信噪比信號無法分辨、計算量大等缺陷，故有許多改進算法被提出。該文從MUSIC算法基礎分析入手，分別從陣元數目、陣元間距等參數方面、相干信號方面以及在定位應用方面等幾個方面對近幾年MUSIC算法的研究進展進行了綜述，并對MUSIC算法的研究趨勢進行展望。

關鍵詞：智能天線? MUSIC算法? 陣元? 陣列信號處理

中圖分類號：TN92 ? ?文獻標識碼：A 文章編號：1672-3791（2019）09（c）-0005-02

Schmidt等人在1979年提出了多重信號分類（Multiple Signal Classification， MUSIC）算法。該算法開辟了空間譜估計算法的新紀元，推動了特征結構算法的興起和發展[1]。在此之前，相關算法都是直接處理陣列接收到的數據協方差矩陣，MUSIC算法的基本思想則是特征分解任意陣列輸出數據的協方差矩陣，從而得到與信號分類相對應的信號子空間和與信號分量相正交的噪聲子空間，接著構造兩個子空間的正交空間譜函數，從而通過搜索譜峰檢測出信號的波達方向（Direction of Arrival，DOA）[2]。

1? 經典MUSIC算法測向原理

1.1 一般陣列數學模型

在適當的信號數學模型的基礎上，能夠對空間譜估計算法進行合理的推導以及參數的正確估計，因此，建立一個與實際情況相符的數學模型至關重要。

在空間譜估計算法中，線性陣列和圓形陣列是兩種最常用的天線陣列。大多數文獻中提到的算法原理都是基于均勻線陣的模型，其原因在于線性陣列結構簡單，推導容易，算法易于實現。但是，在使用均勻線陣時，其天線間距不能大于半波長。否則，在估計時會出現模糊值，無法區分模糊值與真值[3]。

1.2 任意立體陣模型

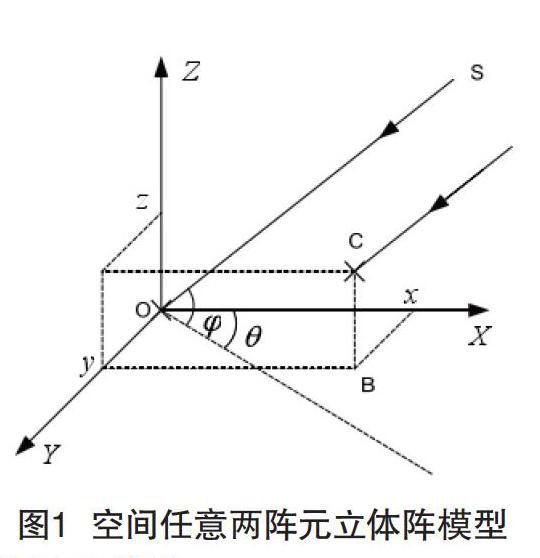
假設在空間中的任意位置有兩個陣元O和C，以陣元O為坐標原點建立一個空間直角坐標系，如圖1所示。陣元C坐標為（x，y，z），SO為信號射入方向，記SO在平面XOY上的投影與X軸的夾角為θ、SO與平面XOY的夾角為?。記陣元C在平面XOY上的投影為B，在B處引入一個虛擬陣元，那么陣元O和C之間的波程差等于陣元O和B之間的波程差加上陣元B和C之間的波程差。

2? 改進的MUSIC算法

2.1 天線陣元數、陣元間距等參數方面的改進

在實際測向中，天線陣元數、陣元間距、快拍數和信噪比都對MUSIC算法的性能影響很大，設置合理的天線陣元數與陣元間距，以及合理的快拍數和信噪比，能有效加強MUSIC算法的性能。

楊桂芹等[4]研究人員認為，在陣列信號模型的精確條件下獲得MUSIC算法的超分辨率。諸如陣列元素的數量、元素的間隔、信噪比和快照的數量等因素將對MUSIC算法的分辨率產生一定的影響。通過仿真，綜合分析了陣列數、陣列間距、信噪比、快速拍號對音樂算法分辨率的影響。

張濤濤、張興敢[5]研究認為，經典MUSIC算法的統計特性主要是基于陣元數固定且快拍數趨于無窮的情況。在有限樣本中，當快拍數不能滿足遠大于陣元數的條件時，DOA估計會有偏差。對于寬帶信號，利用相干信號子空間（Coherent Signal-subspace Method，CSM）方法構造聚焦矩陣，將不同頻率的信號子空間映射到相同的參考頻率;并針對陣列陣元數較大且快拍數受限時經典MUSIC算法估計精度不高的情況，利用改進后的Spike-MUSIC算法，提高DOA估計精度。通過MonteCarlo仿真實驗，分別估計了在不同信噪比下DOA估計的誤差。仿真結果表明，相對于普通的CSM方法，基于Spike-MUSIC算法改進的CSM方法在寬帶DOA估計中具有更高的精度。

胡榮飛等研究人員[6]分析了在不同陣元數、快拍數、陣元間距和信噪比的情況下對MUSIC算法性能的影響，對實際天線陣列的設計和數據的優化處理有一定的指導意義。他們主要從天線陣列的陣元數、快拍數、陣元間距和信噪比的變化對MUSIC算法性能的影響進行了分析。研究結果表明，增加陣元數和快拍數都會提高MUSIC算法的譜峰分辨率，但同時也增加了數據的處理難度和持續時間。

2.2 相干信號方面的改進

MUSIC算法只能單獨對非相干信號源進行估計，為使信源相干或相關時仍能獲得正確的DOA估計，許多研究學者采用空間平滑技術對相干信號進行預處理來修正 MUSIC算法。

趙謙等[7]研究人員認為，傳統改進MUSIC算法是通過對接收信號協方差矩陣作預處理，分解信號協方差矩陣，得到正交于噪聲子空間的信號子空間，從而減小噪聲的影響。但當信號間隔很小時，傳統改進MUSIC算法不能通過降低信噪比來分辨信號。基于這個問題，修正的MUSIC算法在信號子空間正交于噪聲子空間的基礎上，充分利用噪聲子空間及其特征值來修正噪聲子空間，進而構造譜峰搜索函數進行信號估計。仿真實驗證明，修正后的MUSIC算法在低信噪比、小信號間隔且存在相干信號時能準確地估計出傳統改進MUSIC算法不能估計的信號。

尤國紅等研究人員[8]在均勻圓陣的波達方向估計中引入了循環平穩理論，提出了一種基于圓陣的擴展循環MUSIC算法。同時，利用循環相關系數和循環共軛相關系數的信息，有效抑制了干擾和噪聲在同一頻帶內的影響，實現了興趣信號與干擾信號的有效分離。仿真結果表明，該算法具有較高的DOA估計精度和較好的多信號分辨能力，且突破了經典MUSIC算法中信源數不能超過陣元數的限制。

袁自月、楊國[9]研究了求根MUSIC算法、基于空間平滑技術的MUSIC算法、改進MUSIC算法及修正MUSIC算法。通過仿真分析了角度間隔、相干信號對改進MUSIC算法分辨率的影響。上述幾種改進MUSIC算法進一步發揮了該算法高分辨率的優勢，有利于其在智能天線方面的應用。

3? 結語

MUSIC算法的提出標志著空間譜估計測向技術向實際的應用邁出了重大的一步，MUSIC算法的發展已經經歷了很長的一段時間，它所具有的獨特優勢使得其被廣大研究者不斷優化和使用。該文從MUSIC算法天線陣元數、陣元間距、快拍數、信噪比和相干信號以及在智能天線的應用等方面進行了綜述，可以看出MUSIC算法在以下幾方面的改進依然需要進行深入的研究。

（1）信號源數的精確估計。目前，大多數高分辨MUSIC算法都是在已知信號源數的前提下提出的，MUSIC算法的實際應用在一定程度上有所限制。例如：MDL準則在信噪比較小時誤差概率較大，平滑秩法也只有在信噪比較高時能夠估計相干源的結果。因此，研究符合實際應用環境的實時、穩健的信號源數具有重要的現實意義。

（2）穩健的DOA估計算法。現有的研究大多只考慮了陣列的幅相誤差、互耦誤差和位置誤差。魯棒性算法的一個重要方向就是陣列校正和角度參數聯合估計。陣列校正和角度估計都可歸于參數優化問題。因此，構造優化函數和優化函數的快速算法的均值求解仍值得進一步研究。

參考文獻

[1] R.O.Schmidt.Multiple emitter location and signal parameter estimation[J].IEEE Transa ctions.on Antennas and Propagation，1986，34（3）：276-280.

[2]`WANG Buhong，WANG Yongliang，CHEN Hui.Weigh-ted spatial smoothing for direction of arrival estimation of coherent Signal[J].IEEE AP.And NR，2002（6）：668-671.

[3] 藍曉宇.提高空間譜估計分辨率的超分辨測向算法研究[D].哈爾濱工程大學，2012.

[4] 楊桂芹，房琪，胡瀅.陣列天線DOA估計中MUSIC算法性能綜合分析[J].蘭州交通大學學報，2011，30（3）：86-91.

[5] 張濤濤，張興敢.基于改進MUSIC算法的寬帶DOA估計[J].南京大學學報：自然學版，2016，52（5）：932-938.

[6] 胡榮飛，林自豪，楊娟.空間譜估計經典MUSIC算法性能分析[J].數字通信世界，2018（10）：34-35.

[7] 趙謙，董民，梁文娟.DOA估計算法的一種修正MUSIC算法的研究[J].計算機工程與應用，2012，48（10）：102-105.

[8] 尤國紅，邱天爽，夏楠，等.基于均勻圓陣的擴展循環MUSIC算法[J].通信學報，2014，35（2）：9-15.

[9] 袁自月，楊國.MUSIC算法的性能比較[J].電子科技，2014， 27（7）：19-22.