K均值聚類改進與行駛工況構建研究

劉子譚 朱平 劉旭鵬 劉釗

（1.上海交通大學，上海 200240；2.上汽大眾汽車有限公司，上海 201805）

1 前言

行駛工況是通過數據分析所構建的一個區域內一系列代表性的速度-時間數據，可以模擬真實的交通狀況，以測試車輛尾氣排放和燃料消耗。此外，其在交通協同控制、新車評價、風險評估和車輛的設計、選型、匹配和控制策略等方面有著廣泛的應用[1-3]。

常用的行駛工況構建方法是短行程法，將數據劃分成短行程片段，通過分析片段特征參數組合生成對應的行駛工況[4]。Lin 等采用短片段劃分以及隨機過程選擇方法構建了行駛工況[5]。Fotouhi和Montazaeri 描述了基于短行程和K 均值聚類方法的汽車行駛工況構建過程，將開發的行駛工況特征與FTP-75、聯合國歐洲經濟委員會（Economic Commission for Europe，ECE）汽車法規和市郊循環工況（Extra Urban Driving Cycle，EUDC）進行了對比分析[6]。同濟大學胡志遠利用短行程、主成分分析、聚類分析等方法對上海市公交車進行研究，生成了最優短行程組合[7]。吉林大學秦大同等利用K 均值聚類算法與工況選擇方法構建了較為精準的區域行駛工況[8]。李孟良等學者采集了北京、上海和廣州車輛行駛速度等運動學特征，生成3個城市的工況并與ECE 15 工況相比較，說明中國城市行駛工況的特點[9]。彭美春等學者沿廣州市中心區2 條典型公交線路進行試驗，得到廣州市公交車行駛工況并與歐洲瞬態循環（European Transient Cycle，ETC）城市工況進行了比較[10]。

我國汽車行駛工況方面的標準、試驗方法、測試手段等全面沿用新歐洲行駛工況（New European Driving Cycle，NEDC），但其與中國的相似程度較低。李孟良等學者根據采集的北京市、上海市、廣州市實際道路工況提出了QC/T 759—2006《汽車試驗用城市運轉循環》，但該工況提出較早，對當前廣州市實際交通狀況的適應性有待驗證。因此，構建較為精確的廣州市交通特征行駛工況對于分析廣州市交通狀態，以及廣州市機動車排放測試、新車仿真有著重要價值。

本文利用短行程法、主成分分析及聚類方法，并針對K均值聚類穩定性較差的缺陷進行改進研究，將改進后的聚類方法應用于工況構建，生成了廣州市行駛工況并與美國、歐洲等地區的典型行駛工況進行比較，給出廣州市工況的特點。

2 行駛工況構建流程與理論方法

2.1 短行程法構建工況流程

先將數據劃分成短行程片段，再根據片段特征參數，將具有相似特征的片段聚合成3 類，對生成的類數據集采用一定的片段拼接算法生成行駛工況[7,11]，本文采用的行駛工況構建流程如圖1所示。

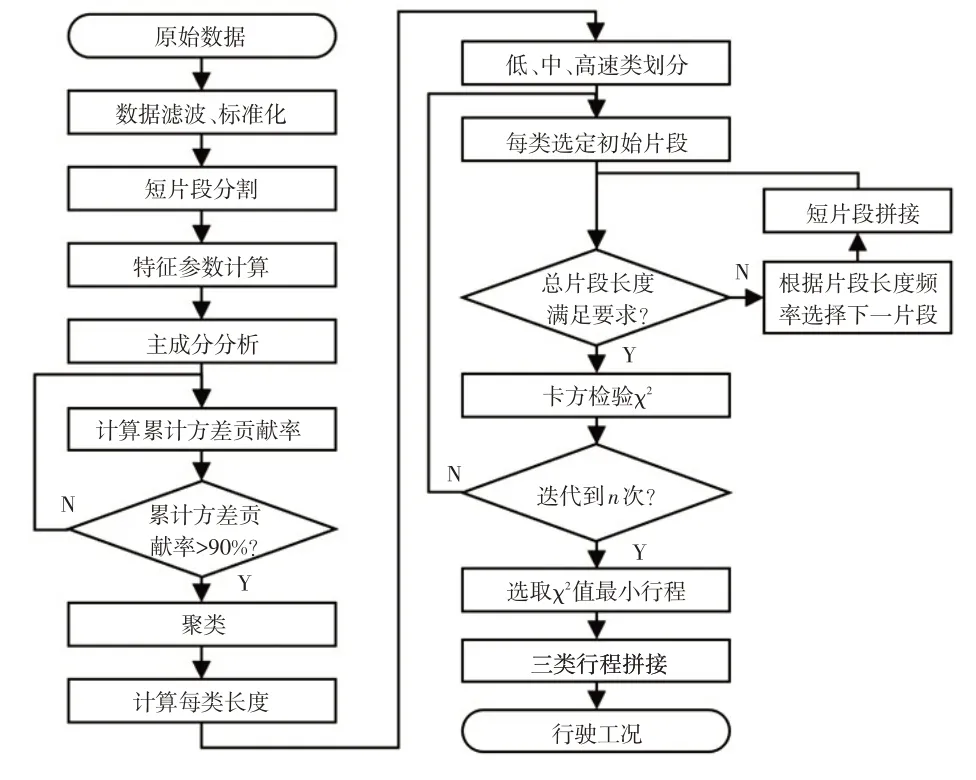
圖1 短行程構建流程

2.2 主成分分析

主成分分析法是一種多元統計方法，可以通過較少的綜合變量盡可能多地反映原變量的信息。本文數據量大、數據維度多，且各維度之間有一定的信息重疊，通過主成分分析能夠大幅減小數據規模，提高計算效率。

2.3 聚類理論

K 均值聚類（K-Means）作為最常用的聚類算法之一，具有算法簡單、收斂速度快等優點。K 中心點聚類（K-Medoids）與K 均值聚類不同，選用類中位置居于最中心的對象作為迭代過程新聚類中心。模糊C 均值算法（Fuzzy C-Means，FCM）與K 均值聚類方法的主要區別在于FCM采用模糊劃分，使得每個數據點用[0,1]區間內的隸屬度來確定其屬于各個類的程度。高斯混合模型（Gaussian Mixture Models，GMM）每個維度用均值和標準差（方差）描述簇的形狀。

3 數據采集與預處理

3.1 數據采集

行駛工況的構建采用數據解析方法，對于樣本量和樣本質量有一定要求。表1 顯示了收集數據的基本信息。每日數據由多個短行程組成，數據記錄從汽車起動開始到汽車熄火結束。車型選擇需要考慮用戶覆蓋不同的職業和年齡段，選擇了A0 級、A 級、B 級車型共計20 輛。經過6 個月的廣泛采樣，共采集了廣州市2 800余萬條行駛數據。

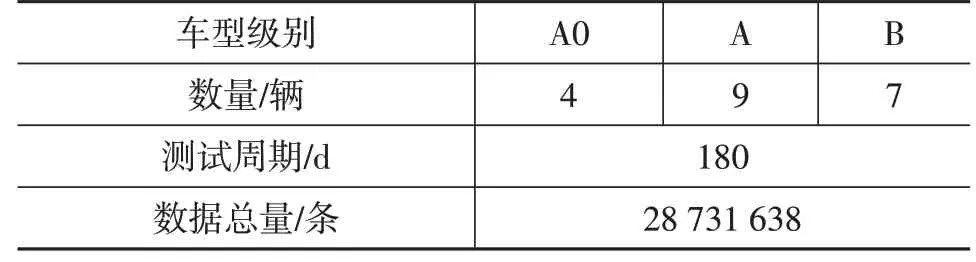
表1 數據采集基本信息

3.2 數據預處理

短行程是汽車行駛過程中一個怠速開始到下一個怠速開始的運動學片段，可以看作怠速段與運動段的組合。通過道路試驗得到汽車運行過程中的速度-時間數據，將數據分割成111 321 個短行程片段。為了描述短片段的特征，選用行駛距離、最高車速、最大加速度、最小減速度、平均加速度、平均減速度、加速度標準差、平均車速、平均運行車速、速度標準差、減速時間、加速時間、怠速時間、巡航時間、片段時間作為特征參數。

對原始數據進行主成分分析，結果如表2所示。選擇使累計貢獻率達到90%的前4 個主成分代表所有原始變量，使得主成分方差貢獻率達到91.28%。

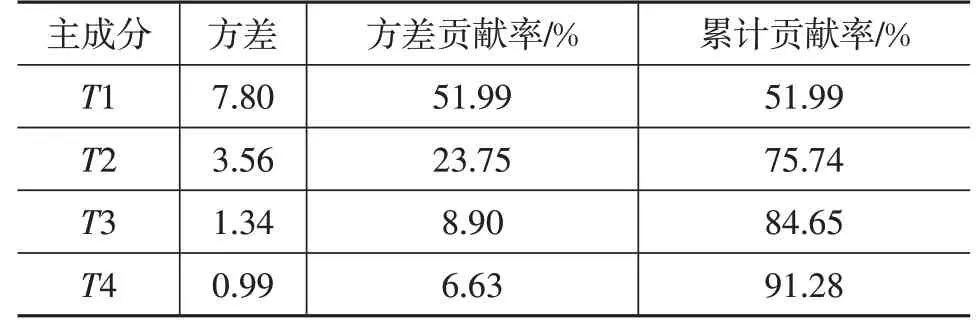
表2 主成分貢獻率及累計貢獻百分率

4 聚類方法對比分析

聚類方法多種多樣，其效果對行駛工況構建的精度也有重要影響。行駛工況構建過程中涉及大量數據的處理，根據聚類方法適用性選取K 均值聚類、K 中心點聚類、模糊聚類與高斯混合聚類進行比較分析。

為了判斷聚類方法的優劣，聚類中心設為3 個，分別運用4種方法進行10次聚類并對結果進行計算分析。

4.1 聚類穩定性

短片段的速度特征是描述片段的重要參數，每個類的速度分布也能較直接地的反映聚類效果，10 次聚類每一類的最大速度頻率分布如圖2所示。

圖2 最大速度頻率分布

為了描述聚類穩定性，計算相關變量，比較聚類中心偏差值ε，ε越小，穩定性越高。計算公式為：

式中，K為聚類中心數量；N為試驗次數；nij為第i次試驗第j類聚類中心坐標；-n為N次試驗的平均值。

ε的計算結果如表3所示。由圖2、表3可知，4種方法生成的類速度分布整體趨勢相似，且每類的速度分布有明顯差別，因此可將3 類劃分為低、中、高速類。此外，結果反映出了聚類結果的穩定性：模糊聚類10次聚類頻率分布曲線幾乎重合，偏差小、穩定性好；K中心點聚類次之；高斯混合較為發散；K 均值聚類則出現了混亂的結果，偏差值較大。

表3 聚類穩定性評價指標

4.2 樣本適應性

速度、加速度聯合概率分布是描述工況狀態的重要指標，也是短行程拼接篩選的依據。每一類內部速度、加速度聯合分布差異越小，越易篩選到與該類聯合分布匹配的短片段。

輪廓系數（Silhouette Coefficient）是描述輪廓團聚性的變量。對于單個樣本，計算公式為：

式中，a為其與同類別中其他樣本的平均距離；b為其與距離最近的不同類別中樣本的平均距離。

對于一個樣本集合，輪廓系數是所有樣本輪廓系數的平均值。輪廓系數取值范圍是[0,1]，同類別樣本距離越相近且不同類別樣本距離越遠，即數值越大，團聚性越高。

圖3所示為4種聚類方法平均速度與平均加速度聯合分布情況，表4 所示為4 種適應性指標。可得兩種K聚類中各類的速度、加速度聯合分布具有更明顯的團聚性，低速類的平均加速度整體較高，高速類的平均加速度整體較低，這與實際低、高速行駛狀態相一致，說明K聚類更適合該樣本，其中K均值聚類樣本適應性最好。

4.3 聚類時間

表5 所示為4 種聚類方法的平均聚類時間，由圖5可以明顯看出K 均值聚類在計算時間方面較其他聚類算法有明顯優勢。

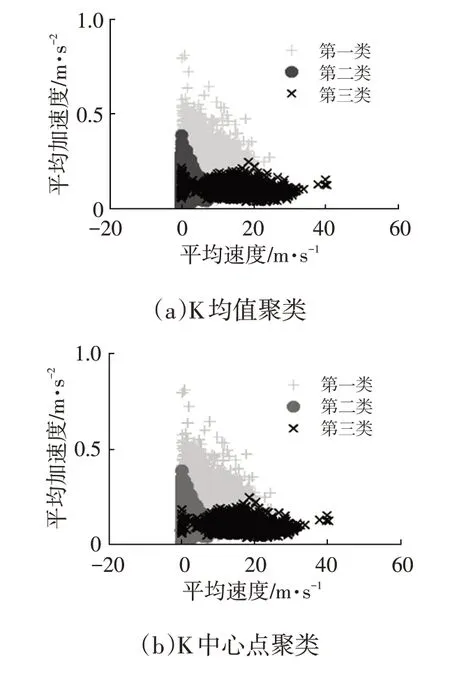
圖3 平均速度與平均加速度聯合分布

表4 聚類適應性評價指標

表5 聚類平均時間

4.4 緊密性與分離性指標

為了量化描述聚類效果以及聚類的穩定性，采用緊密性（Compactness）CP與分離性（Separation）SP指標。前者描述各點到聚類中心的平均距離，越小說明同一類緊密度越高，效果越好；后者描述各聚類中心兩兩之間的平均距離，越大說明不同類間隔性越高，效果越好。緊密型指標和分離性指標的計算方法分別為：

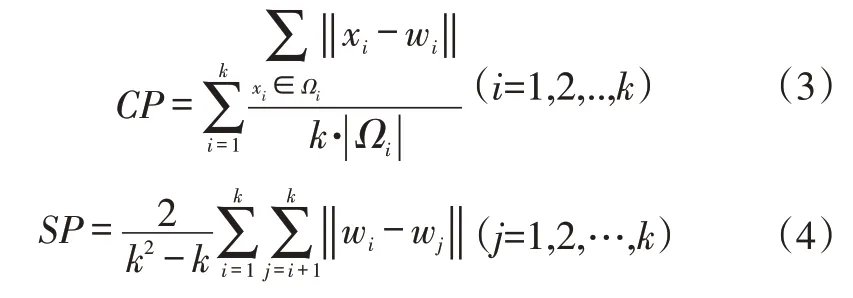
式中，k為聚類中心個數；Ωi為第i個聚類集合；wi為第i個聚類中心；xi為第i個聚類所包含的元素。

表6 所示為4 種聚類CP與SP指標的均值與方差。4 種聚類方法得到的CP與SP指標均值接近，且聚類緊密度與間隔度此消彼長，但指標方差差別較大，模糊聚類方差最小，K 中心點聚類次之，高斯混合聚類最大，K均值聚類較大，這與穩定性指標分析結果相吻合。

圖4、圖5 分別 為4 種方法10 次 聚類CP值 與SP值。10次聚類結果中模糊聚類與K中心點聚類指標變動小，高斯混合整體波動較大，而K 均值聚類出現了尖點。因此，4 種聚類方法準確性效果相似，但穩定性有差異。其中，模糊聚類、K中心點聚類穩定性較好，高斯混合聚類較差，而K均值聚類除了一次偏差較大的不合理聚類外，其余結果較穩定。

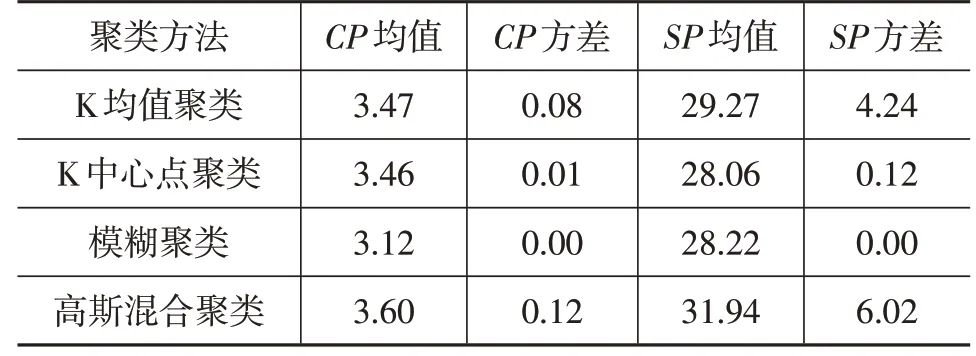
表6 CP與SP均值與方差

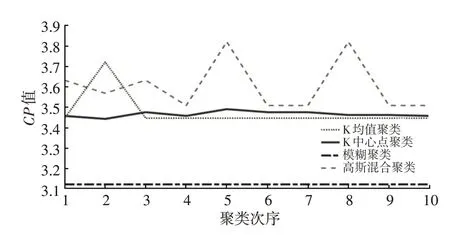
圖4 10次聚類CP值

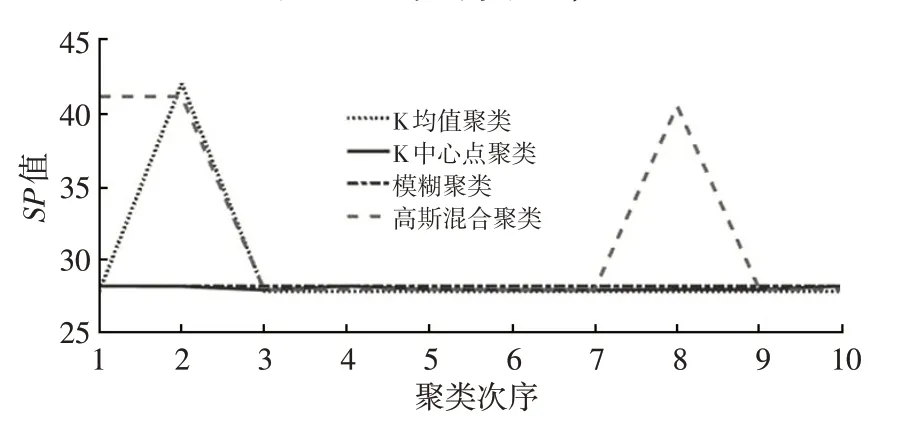
圖5 10次聚類SP值

綜上，K均值聚類綜合性能較優，樣本適應性最好，聚類效率最高，但其穩定性有待改進。

5 K均值聚類改進研究

K均值聚類對初始值較敏感，結果發生突變的主要原因是初始聚類中心選到了數據集中的邊緣點或者孤立點。針對這一問題，對數據集進行統計學分析。

在數據空間中，通常認為處于低密度區域的點為噪聲點[12]。由表7主成分統計特征參數可得，主成分均值均為0，每一維數據具有正態性，且其置信度90%區間范圍相對于原有區間范圍大幅縮小。每個維度都采用置信度90%區間范圍計算的聯合分布概率為75.98%，點平均密度增加為原來的15 萬倍，即舍棄了原空間中的邊緣點與孤立點。

因此采用置信度90%區間作為K 均值聚類初始聚類中心的選擇區間，10次聚類結果如表8所示，改進前、后聚類中心偏差減小，輪廓系數增加，CP和SP指標方差減小，穩定性提高顯著，且計算效率相近。

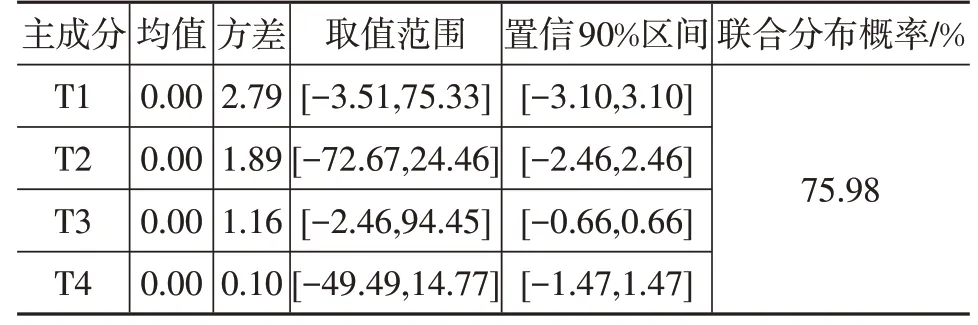
表7 數據集統計特征參數

表8 改進前、后參數對比

6 行駛工況構建驗證

根據某汽車企業的測試標準，行駛工況時間長度為1 800 s，其中低、中、高速時間分別為413 s、920 s和467 s，利用改進的K均值聚類法構建廣州市行駛工況如圖6示。

選取9 個指標對生成的工況進行驗證，表9 為試驗數據與擬合工況參數對比結果。可見，改進方法生成的廣州市道路行駛工況各項誤差均小于10%，低、中、高速類以及整體平均相對誤差為小于6%，運動學特征較吻合。

圖6 廣州市行駛工況

行駛工況的主要運動學特征為汽車行駛的速度和加速度，且兩者具有強相關性。因此，能準確描述數據集運動學信息的行駛工況應具有與原數據集相似的速度-加速度聯合分布。由表9 可知，廣州市低、中、高速以及整體速度-加速度聯合分布概率卡方檢驗值均小于0.1，即卡方檢驗合格，說明擬合工況與試驗數據顯著相關。通過運動學特征比較以及速度-加速度頻率分布卡方檢驗證明，利用本研究方法所得到的行駛工況能夠反映實際道路交通狀況。

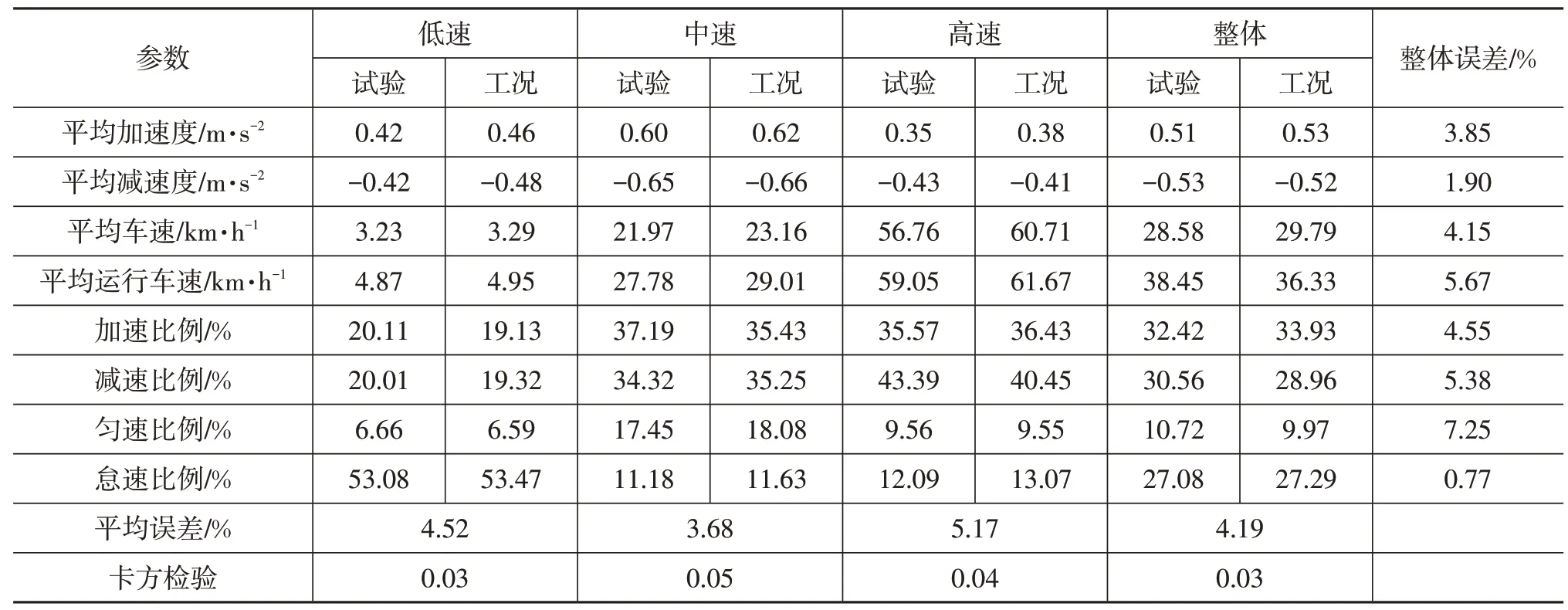
表9 試驗與擬合工況參數對比

將廣州市行駛工況與國際上常用的行駛工況全球統一輕型車油耗測試規程（World Light Vehicle Test Procedure，WLTP）、NEDC、美國城市道路循環（Urban Dynamometer Driving Schedule，UDDS）、日本工況JC08、中國汽車試驗用城市運轉循環（QC/T 759—2016）相比較，結果如圖7所示。由圖7可以看出：廣州市行駛工況怠速比例高達27%，速度分布頻率隨著速度的提高逐漸降低，最高速度約為110 km/h；而UDDS、NEDC 以及QC/T 759 循環中速段頻率高于低速段；WLTP 速度分布較平均；JC08 低速分布頻率最高。QC/T 759 循環最高速度為90 km/h，顯然不符合廣州市實際交通工況。因此，廣州市工況低速段比例較高、平均速度較低，與其他代表性工況有一定差異。

圖7 廣州市行駛工況與世界典型行駛工況速度頻率分布對比

對廣州市工況的相關運動學參數分析可得，廣州市車輛運行加、減速比例高達60%以上，加、減速頻繁，起停過程多、怠速比例高，交通狀況較擁堵，相應的燃油消耗和尾氣排放高，交通狀況有待改善。因此，中國現行NEDC 以及QC/T 759 工況不能完全反映廣州市的實際交通狀況，而本文構建的廣州市行駛工況代表性、準確度高。

7 結束語

本文以廣州市為例，利用短行程法、主成分分析法對采集的數據集進行處理。對4 種聚類方法進行比較分析，并對K 均值聚類進行了改進，改進算法穩定性大幅提高，生成的行駛工況平均相對誤差小于6%。

通過分析廣州市試驗數據與行駛工況的特征參數，驗證了工況的準確性。廣州市工況與世界典型工況對比結果表明，廣州市行駛工況加減速比例高、低速段占主導、交通狀態較擁堵，與其他代表性工況有一定差異。本文構建的工況在速度分布等方面較中國現行的測試工況NEDC 和QC/T 759—2016 更符合廣州市的交通特點。