車轍斷面非均勻積水對車輛安全性影響的仿真分析＊

燕姣 李巖 惠冰

（1.西安航空學院，西安 710077；2.長安大學，西安 710064）

1 前言

車轍是瀝青路面上由車輛載荷引起的縱向持久下凹形變[1]，降雨時車輛在車轍路面上行駛會因輪胎無法及時排出積水而發生水漂。此外，橫向非均勻積水車轍使道路表面的附著系數呈現橫向不均勻分布，導致車輛左、右輪胎受力不均而使車輛偏轉。因此，準確描述車輛行駛時偏移量與車轍斷面積水深度的關系，可為車轍安全風險評價與車轍嚴重程度評估提供參考。

目前，車轍積水深度不易測量，通常將采用直尺法或包絡線法確定的最大車轍深度[2-3]，即（干燥）車轍深度作為“車轍積水深度”。另外，國內外學者Wenting、Fwa、雷明軒、徐世法、張敏等人[4-8]對積水車轍的行車安全分析也僅采用了最大車轍深度。上述研究在輪胎-積水模型構建中，簡化了車轍斷面形態，將積水車轍斷面假設為矩形，這樣的假設對車轍斷面積水面積的估計偏高。而且，上述研究未考慮整車發生水漂時的狀態，僅假設4個車輪中有1個發生水漂即面臨危險，該假設同樣過高地估計了風險。因此，僅采用最大車轍深度無法反映車轍斷面形態對積水深度、寬度和面積等造成的影響[9]，而積水深度和寬度會影響車輛與積水路面接觸的程度，進而影響安全性分析結果。

本文考慮車轍形態對車轍積水深度的影響，利用3D 線激光檢測系統采集的真實車轍斷面，假定車轍在縱向無變化，將車轍橫斷面上的積水深度進行細分，對比細分前、后車輛在積水車轍中的行駛安全性。

2 不對稱積水車轍的側滑機理分析

本文主要針對車輛在左、右車轍積水深度不同的情況下發生側滑的安全風險進行分析。車輛直行遇積水發生側滑的狀態如圖1 所示。不同的車轍積水深度導致車轍的附著系數不同，因此，車輛朝著積水多即附著系數較低的一側偏轉。研究表明[10-11]，路面附著系數越低，車輛橫向側滑量對車輛橫向穩定性的影響越敏感。車輛橫向側滑量越大，駕駛員對車輛的控制能力越低，車輛發生危險的可能性就越高，所以本文用車輛橫向偏移量來表征車輛的橫向穩定性。

圖1 車輛直行遇積水后的橫向滑移

3 研究方法

本文提出的考慮車轍斷面積水深度橫向不均勻性的整車橫向穩定性評估方法如圖2所示，通過車轍積水深度、輪胎花紋深度、車輛行駛速度計算單一輪胎與積水路面間的附著系數，在CarSim中建立多自由度整車模型，進行不同附著系數分布情況下的對比仿真，評估車轍左、右積水深度不對稱情況下直行車輛的橫向穩定性。

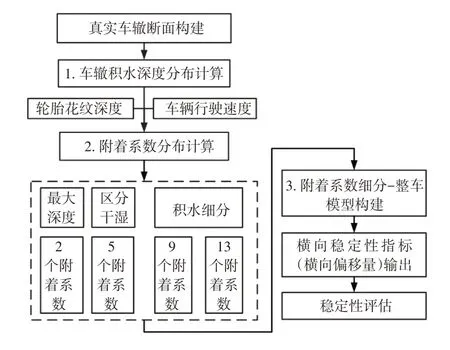
圖2 不對稱積水車轍整車橫向穩定性評估

基于長安大學3D 激光檢測車（見圖3）獲取了陜西省西商高速公路的真實車轍斷面高精度、高密度點云數據，檢測車將2 個線激光檢測系統（Gocator 2380）組合使用，檢測寬度可達2～4 m。檢測橫斷面每條輪廓包含2 560 個數據點，X方向分辨率為0.375～1.100 mm，Z方向分辨率為0.092～0.488 mm。

圖3 長安大學3D激光檢測車

為確保車轍積水深度的計算精度，檢測的橫斷面需要去除異常點和不光滑點。依據AASHTO PP69[12]的規定，使用移動平均法來平滑車轍橫斷面高程點云數據，過濾窗口尺寸越大，平滑后的表面越光滑。移動平均法過濾后的輸出數據為：

式中，z[i]為輸入數據；m=50 mm為過濾窗口大小。

圖4所示為濾波前、后的車轍斷面。

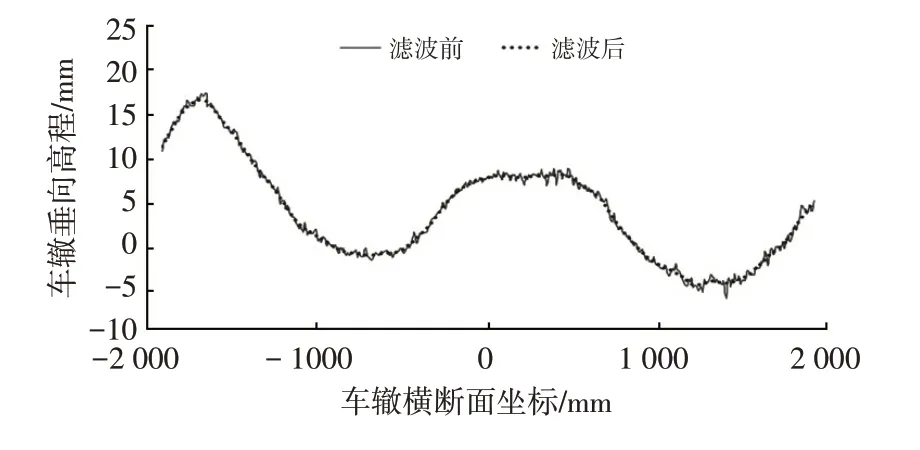
圖4 濾波前、后的車轍斷面

3.1 車轍積水深度分布計算

以積滿水的車轍為研究對象，故積水深度為車轍曲線上各點到積水線函數的距離。

3.1.1 斷面極大值點確定及篩選

車轍斷面的極大值點決定了積水區的邊沿點。由于車轍橫斷面存在高低起伏，相鄰較近的斷面可能存在1 個或1 個以上的極值點，因此需要依據極值點所在的路面分區對極大值進行篩選。依據斷面位置和實際工程經驗將斷面劃分為3 個區域，即左、右輪跡帶和道路中心線區域，每個區域內僅需1個極大值點。由左至右分別標記為1、2、3，如圖5 所示，2、3 點為積水邊沿點。使用美國佛羅里達交通部（Florida Department of Transportation，FDOT）對輪跡帶的定義將車道分區。定義中間非輪跡帶與兩側輪跡帶寬度相同，均為車道寬度的1/4，兩側非輪跡帶分別為輪跡帶寬度的1/2，即車道寬度的1/8。

3.1.2 積水線函數確定

以積水邊沿2、3 點向左延伸與車轍曲線的交點為4、5，因此左車轍積水線函數為y=Zl=Z2，右車轍積水線函數為y=Zr=Z3。

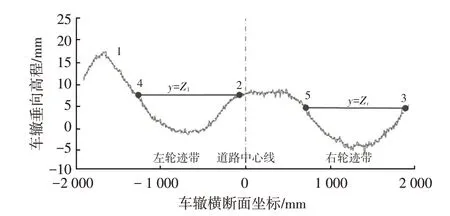
圖5 車轍積水深度計算

3.1.3 積水深度計算

積水深度h為：

式中，hli、hri分別為左、右車轍積水區域第i個積水段落的積水深度；Zi為車轍曲線上的各點高程；Xi為車轍曲線上各點對應的橫斷面坐標。

3.2 附著系數分布計算

3.2.1 附著系數計算

車輛與積水路面間附著系數的計算依托于輪胎-積水三維有限元模型的建立。Yurong 等人[13]較早地運用ABAQUS 建立了三維有限元模型，得到了不同路面（干、濕）條件下的抗滑擺值；東南大學的Cao 和張海泉[14-15]通過有限元計算得到的附著系數回歸模型與季天劍[16]利用Ansys 軟件、董斌[17]利用Fluent 流體動力學軟件得到的附著系數回歸模型差異不大，可以表征輪胎部分滑水條件下附著系數隨行車速度、水膜厚度和花紋深度的變化規律；郭鑫鑫[10]通過Fluent選取重整化群RNGk-ε模型利用非耦合隱式求解法計算輪胎在不同行駛條件和車轍積水深度下輪胎所受到的動水壓力、附著力的變化情況。以上各位學者的附著系數曲線公式趨勢和范圍基本相同。

本文采用文獻[10]中建立的附著系數回歸公式進行橫斷面非均勻積水車轍附著系數的計算：

式中，f為路面與輪胎間的附著系數；v為車速。

3.2.2 附著系數分布計算

車轍橫斷面的積水區域劃分與深度計算，以及由此導致的附著系數的不均勻分布對車輛穩定性評估至關重要，細分結果如圖6所示。

a.2 個附著系數分別使用左、右車轍最大積水深度對應的附著系數f1和f2表示左幅和右幅積水斷面，可以反映車轍左、右不對稱時的情況，但是該假設無法模擬車輛在整個橫斷面側滑行駛結束后，滑移到干燥路面時的狀況。

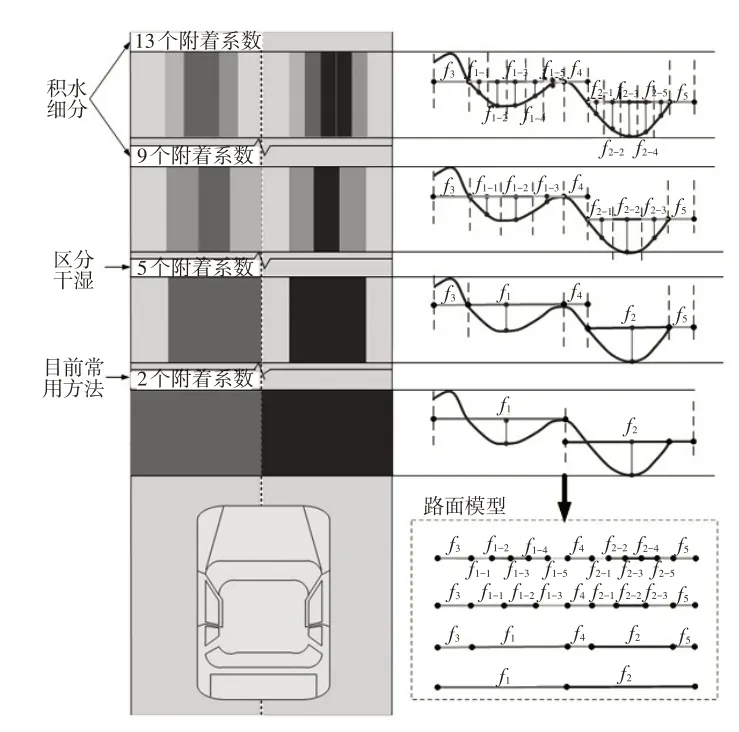
圖6 積水車轍斷面附著系數細分模型

圖6中，對斷面附著系數的細分有多種方式：

b.5個附著系數將道路斷面分為積水和干燥兩部分考慮，f1和f2分別表示積水部分附著系數，f3～f5表示干燥部分附著系數，但是該假設無法模擬車轍本身也存在積水深度不同的情況。

c.9 個和13 個附著系數分別對車轍積水部分進行3 等分和5 等分的均等細分。干燥部分仍然為f3～f5，積水部分被分為3 等份時，附著系數為f1-1～f1-3、f2-1～f2-3，積水部分被分為5等份時，附著系數為f1-1～f1-5、f2-1～f2-5。

在車轍積水的橫向不對稱仿真分析中，假設車轍后一斷面的附著系數與前一斷面附著系數保持不變，以保證橫向車轍不對稱是唯一的控制變量。因而，圖6 的4種情況中車轍沿縱向均保持一致。

此外，由于降雨的作用，前文提到的干燥區域即非積水區域并非完全干燥，而是積水深度為0 mm 的潮濕路面。為講述方便，本文仍然使用“干燥”這一詞。另外，由于水流的浮力作用，車輛在積水區域的高程發生了變化，但是，相比于附著系數變化對車輛橫向偏移量的影響，車轍斷面高程對分析結果的影響較小，因而本文假設干燥和積水區域橫斷面為平面，如圖6中路面模型所示。

4 模型參數設置和仿真結果分析

4.1 模型參數設置

本文借助CarSim 動力學仿真軟件在不同車速、不同車轍積水深度條件下進行仿真，獲取車輛的橫向偏移量，以評估車輛在橫向不均勻的積水車轍上行駛時的穩定性。

4.1.1 車輛和輪胎參數設置

仿真車輛選擇我國常見的兩廂轎車。車輛前、后懸架均采用雙向筒式減振器，配置齒輪齒條式轉向器、麥弗遜式前懸架（帶橫向穩定桿），前輪配置盤式制動器，后輪配置自調式鼓式制動器，前輪驅動。CarSim 中車輛動力學模型的基本參數如表1 所示。車輛行駛速度分別為100 km/h 和120 km/h。此外，輪胎選用目前我國常用的P195/60 R14 86H 型，輪胎內壓為200 kPa，輪胎半徑為326.95 mm，輪胎寬度為225 mm[8]。

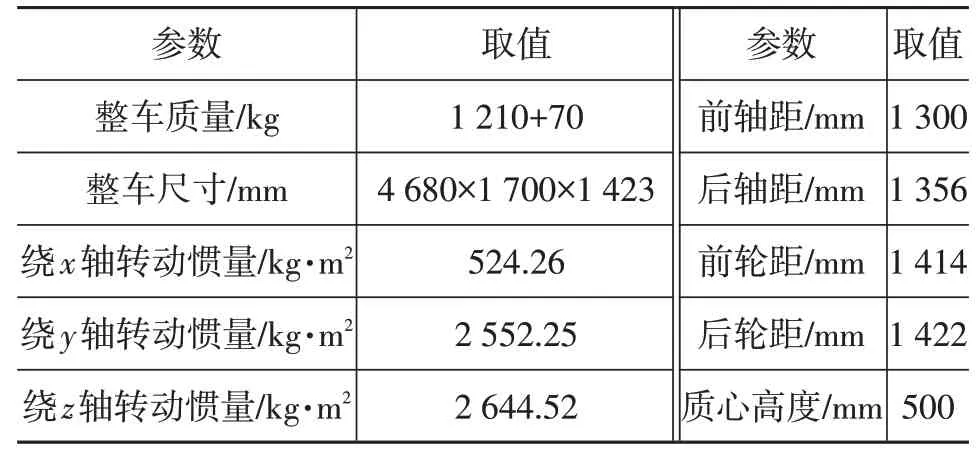
表1 車輛動力學模型基本參數

4.1.2 積水車轍附著系數設置

CarSim 軟件中對附著系數的設置在外部環境數據庫中完成，此外，道路平面、縱斷面線形、橫斷面高程和道路附屬景觀等均在該數據庫中設定。本文在仿真過程中采用Friction Map 函數庫，通過改變橫向坐標對應的附著系數即可實現上述積水車轍附著系數-整車模型的設置。我國《公路技術狀況評定標準》[3]中規定，車轍10～15 mm為輕，15 mm以上為重，因而選用車轍最大深度分別為13 mm和20 mm的輕、重兩種車轍分別進行仿真。為忽略左、右深度差對結果的影響，本文選取的車轍深度差均為4 mm。因而，重車轍的左、右車轍最大深度分別為16 mm 和20 mm，輕車轍的左、右車轍最大深度分別為9 mm和13 mm。

圖7所示為附著系數細分-整車模型構建示意。仿真路段長度設定為900 m，車輛以一定的速度沿道路中心線行駛400 m后（此時車輛加速至一定速度后進入勻速狀態，為車輛預熱階段）進入積水車轍路段。車轍積水路段長度設為500 m，路面寬度為3.75 m。通過改變附著系數的橫向不均勻分布對車輛的橫向偏移量進行分析，并假設車轍沿行車方向均勻。此外，圖7中可以看到車輛側偏1.025 m時駛出車道。因此，本文定義車輛側偏距離達到1.025 m為危險閾值。而且該值隨著車輛尺寸的變化而變化，不同寬度的車輛面臨的危險閾值不同。

4.2 仿真結果分析

車輛以100 km/h 和120 km/h 兩種速度分別在重車轍和輕車轍中仿真分析，其橫向偏移量的變化結果如圖8所示。

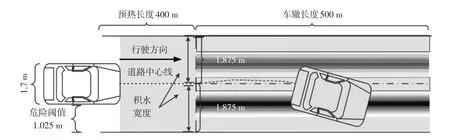
圖7 附著系數細分-整車模型構建

圖8 車轍附著系數細分對橫向偏移量的影響

當行駛速度為100 km/h 時（見圖8a、圖8b），2 個附著系數的情況下，車輛橫向偏移量線性增加。說明橫向加速度未發生變化，這是由于側滑時左、右輪胎下的附著系數不變，導致對輪胎作用力未發生變化。將路面劃分干、濕區域后（5 個附著系數）車輛產生了回偏，這是因為車輛發生側偏后，輪胎與積水路面所接觸區域的積水深度發生了改變，左、右輪胎對應的附著系數由左大右小變為左小右大導致的。在9個和13個附著系數的情況下（見圖8a、圖8b），車輛沒有明顯的橫向偏移，是因為劃分更細致后，積水深度降低，造成附著系數增大，不足以產生偏移。

當行駛速度為120 km/h時（見圖8c、圖8d），車輛偏移量也會隨著細分降低，不同的是由于速度增大，附著系數隨之減小，因此在9個和13個附著系數的狀態下，車輛也發生了橫向偏移。

仿真結果表明：

a.對車轍橫斷面的劃分越細，在相同縱向行駛距離下，橫向偏移量越小。目前常用的使用車轍最大深度（2個附著系數）進行安全分析會高估車輛的安全風險程度。

b.車轍平均深度越大，即使左、右車轍深度差相同，橫向偏移量也會越大。

5 結束語

本文基于連續車轍檢測橫斷面，考慮車轍斷面形態的積水深度分布，建立了附著系數-整車車輛穩定性分析模型。通過對附著系數進行更精密的劃分與計算，得到更為精確的車輛動力學分析結果。得出如下結論：僅使用車轍最大積水深度進行積水安全性分析高估了安全風險；在積水深度劃分精密的情況下，車輛橫向偏移量顯著降低；車輛的側偏與最大車轍深度和左、右深度差存在正相關關系。

本文沒有考慮其他的車輛響應，如橫擺角和橫向加速度與車轍多維度指標的關系，這在以后的研究中應當考慮。