航空發動機多設計點熱力循環分析方法的構建及應用

鄭華雷，王召廣，蔡建兵，黃 興

(中國航發湖南動力機械研究所，湖南株洲 412000)

1 引言

航空發動機熱力循環分析確定了發動機的幾何和全包線內的性能，是發動機設計過程中極為重要的一環。傳統的單設計點熱力循環分析方法(簡稱單設計點方法(SDP))是一個串行的過程，即先選取一個工作狀態作為發動機的設計點進行熱力循環分析，確定發動機在設計點的循環參數。一般情況下，設計點參數確定后，發動機的幾何和全包線性能也隨之確定[1-2]，其設計域不受非設計點需求影響，很難滿足所有狀態的性能需求，需要反復調整、迭代設計點參數。如何選取和調整設計點熱力循環參數，得到合適的設計域，需要設計人員對發動機工作特性有很深的理解，且帶有很大的主觀性，缺乏嚴格的數學判據。與之相對，多設計點熱力循環分析方法(簡稱多設計點方法(MDP))是一個并行的過程，在熱力循環分析之初便以多個典型工作狀態作為設計點，所有設計點上的所有需求和限制都會影響設計域，設計域內的每一個點都嚴格滿足所有工作狀態的性能需求和使用限制。

鑒于多設計點方法的優勢，國外研究人員開始利用多設計點思想進行航空發動機設計。Kestner等[3]采用多設計點思想研究了技術限制、構型對超大涵道比渦扇發動機性能的影響；Bellocq[4]、Perullo[5]、Hendricks[6]等研究了熱力循環參數在不同工作狀態下對槳扇發動機性能的影響；Lehmann[7]、Hughes[8]等開展了新一代通用核心機設計，使該通用核心機可滿足不同構型發動機在不同工作狀態下的性能需求；Schutte 等[9]把多設計點方法和環境設計空間(EDS)結合起來進行熱力循環分析，使發動機能同時滿足性能、使用限制及污染排放、噪聲等要求。但上述研究僅提及多設計點方法的概念及應用效果，對如何構建、求解等實現多設計點方法的具體做法沒有披露。

本文以大涵道比渦扇發動機熱力循環分析為研究對象，提出一種多設計點熱力循環分析的實現方法，并給出了詳細的分析步驟和求解方法。同時，采用具體算例，對比了多設計點方法與單設計點方法的實現過程和得到的設計域，并對兩設計域的差異進行了深入分析。

2 多設計點熱力循環分析步驟

以大涵道比渦扇發動機為研究對象，闡述多設計點熱力循環分析步驟。發動機各工作狀態下的推力為必須滿足的性能需求，以耗油率為一個優化目標(研究為單目標優化，不考慮質量、單位推力等因素)。發動機的技術限制由當前技術水平決定，一般情況下，壓氣機出口壓力、溫度，渦輪導葉、轉子葉片的金屬溫度是較重要的技術限制[10-11]。本研究以高壓渦輪導向器金屬溫度作為技術限制。

2.1 設計點設置

飛機方將根據爬升速率需求，在不同飛行高度、馬赫數下對發動機提出推力要求。為簡化分析，以爬升末端(TOC)狀態替代整個爬升過程；根據起飛質量及滑跑距離，對發動機提出起飛推力要求。為保證熱天的起飛推力，起飛狀態(TO)定義為ISA+25 K；定義巡航狀態(Cruise)的高度、速度及推力略小于爬升末端狀態，巡航狀態的耗油率為優化目標。此外，發動機還有一個最大連續(Max continuous)狀態，以應對發動機失效。一般情況下，大涵道比渦扇發動機最大連續狀態的推力等級與其起飛狀態的一致，本文以起飛狀態代替[12]。

MDP 方法選取所有典型工作狀態作為設計點，再在這些設計點中選取一個氣動設計點(ADP)。壓氣機、渦輪等部件由氣動設計點的設計參數和特性圖(與此部件相似的特性圖或通用特性圖)確定縮放因子，進而確定部件特性。通常，發動機在爬升末端狀態時的換算流量、換算轉速最大，該狀態決定了發動機的最大尺寸。為此，選取爬升末端和起飛狀態為設計點，爬升末端狀態為氣動設計點。

在發動機典型工作狀態、性能需求和使用限制確定之后，需要把設計變量、性能需求和技術限制分配到相應的設計點。發動機模型的主要熱力循環參數，有作為設計變量的燃燒室出口溫度T4、外涵風扇壓比πFⅡ、低壓壓氣機(內涵風扇和增壓級用一個特性圖，在計算時看成低壓壓氣機)壓比πCL、高壓壓氣機壓比πCH、總壓比πC、涵道比B，和不作為設計變量、根據經驗和設計水平取值的壓氣機部件與渦輪部件的效率、燃燒室燃燒效率、燃燒室及通道的壓力損失、轉子機械效率等。

2.2 數學模型構建及求解

確立多設計點及對應的設計變量后，在所有設計點建立平衡方程并求解。公式(1)為平衡方程及與其對應的迭代變量。平衡方程和迭代變量分為兩種類型，一種為設計人員根據性能需求、使用限制之間關系建立的平衡方程(User defined)及與其對應的迭代變量，另一種為使發動機各部件之間滿足功率、流量平衡的平衡方程(Engine matching)及與其對應的迭代變量。

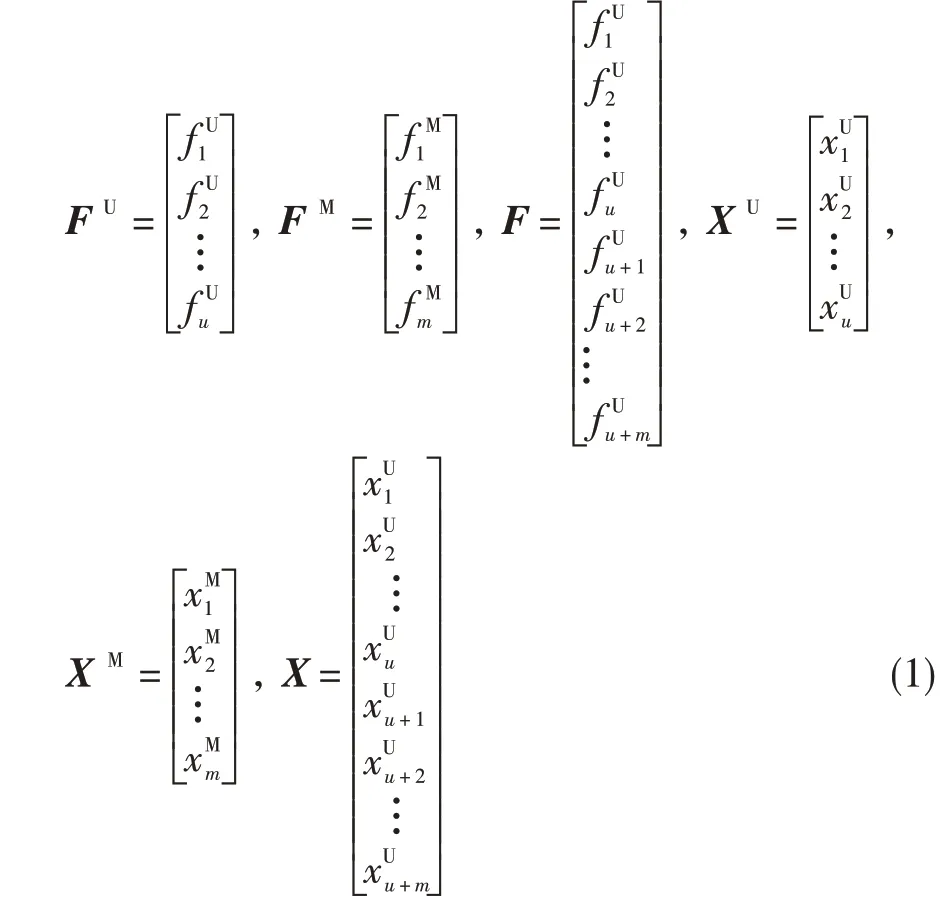
把所有設計點建立的平衡方程整合成一個非線性方程組FX=0 。非線性方程組包含了所有設計點的性能需求和使用限制的平衡方程、各設計點之間滿足發動機部件共同工作的平衡方程，所得到的設計域必然嚴格滿足發動機在各個工作狀態的性能需求和使用限制。數學模型構建完成后，需求解非線性方程組。與普通求解不同，初始形成的非線性方程組的方程數有可能不等于迭代變量，求解器需要判斷進行預處理，使方程數目與變量一致，然后進行求解。

3 具體算例的構建及結果分析

表1 列出了發動機的工作狀態定義、性能需求和技術限制，其中H為飛行高度，Ma為飛行馬赫數，T為環境溫度，F為對發動機需求推力，THNGV為高壓渦輪導向器金屬溫度。后文中的多設計點算例和單設計點算例，都必須滿足此表給出的技術限制和性能需求。

3.1 多設計點方法設計點參數設置

表2 給出了多設計點方法算例的設計點參數設置。πFⅡ、πCL、πCH、πC、B為爬升末端狀態的設計變量。其中，πFⅡ、πC分別為設計域的x變量和y變量，πFⅡ的取值范圍為1.30～1.75，πC的取值范圍為35～65；對于每一組πFⅡ和πC的循環參數，求解器通過尋優尋找最優涵道比，使巡航狀態耗油率最低。根據當前技術水平起飛狀態取T4=1 850 K；根據當前壓氣機和渦輪部件的設計水平，給出了壓氣機部件多變效率ηn,c和渦輪部件多變效率ηn,T，部件的等熵效率由多變效率和壓比(膨脹比)計算得到。高壓渦輪導向器金屬溫度，由燃氣的溫度與流量、冷卻氣體的溫度與流量等氣動參數計算得到，計算方法詳見文獻[13]。

表3、表4 列出了在兩個設計點建立的平衡方程的迭代變量和平衡方程左、右兩側的取值。其中，W代表質量流量，nH和nL分別為高、低壓軸轉速，Wcool,HNGV代表高壓渦輪導向器冷卻氣流量，R為部件特性圖一參考值，求解器利用轉速和R確定工作點在特性圖上的位置。兩個設計點共有10 個迭代變量，11個平衡方程，無法直接求解。這是因為相關高壓渦輪導向器金屬溫度的平衡方程在兩個設計點重復出現，而對應的迭代變量Wcool,HNGV只有一個，求解器需在求解過程中進行判斷，對非線性方程組進行重構，只保留溫度較高的平衡方程，最終形成10個平衡方程進行求解。

表3 爬升末端的平衡方程Table 3 Equilibrium equations at TOC

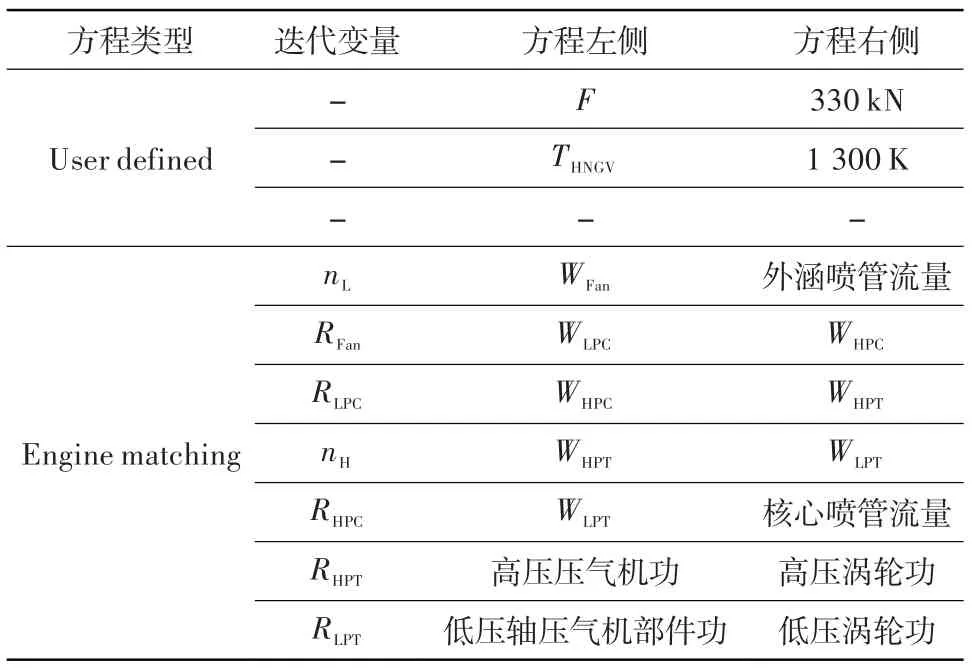
表4 起飛狀態的平衡方程Table 4 Equilibrium equations at TO

3.2 單設計點方法設計點參數設置

表5 為單設計點方法算例1(SDP1)的設計點參數設置。為更好地比較多設計點方法和單設計點方法設計域的差異，在爬升末端狀態，兩種方法的πFⅡ與πC取值范圍一致，πCL、B的計算方法一致，πCH、ηn,c和ηn,T取值一致，推力需求一致。單設計點方法在設計點計算之前假設了Wcool,HNGV和爬升狀態的T4，且不隨πFⅡ和πC變化，而在多設計點方法中這兩個變量為迭代變量(表3)。

表5 單設計點方法算例1 的設計點參數設置Table 5 Parameters for SDP1 of single design point method

3.3 結果分析

對多設計點方法算例與單設計點方法算例設計域的不同之處進行了對比及原因分析，并比較了兩種方法的優劣。圖例中的πFⅡ和πC為爬升末端的設計變量，耗油率為巡航狀態耗油率，推力為起飛狀態推力，高壓渦輪導向器金屬溫度為最高金屬溫度。

3.3.1 多設計點方法算例與單設計點方法算例1 設計域的對比

圖1 為多設計點方法算例與單設計點方法算例1 的巡航耗油率對比。由圖可知，多設計點方法算例耗油率隨πC和πFⅡ的增加均為先減小后升高，存在一個最優的πC和πFⅡ組合使得發動機耗油率最低。單設計點方法算例1的耗油率隨πC的增加同樣為先減小后升高，但當πC在60～65范圍內時耗油率的變化幅度很小。兩種算例的設計域存在明顯差別，最優耗油率及對應的πC和πFⅡ也不同。多設計點方法算例的耗油率最優結果0.055 5 kg/(h·N)，πFⅡ=1.45，πC=50，B=10.2，對應的Wcool,HNGV=0.118，爬升末端T4=1 590 K。單設計點方法算例1 的耗油率最優結果0.055 3 kg/(h·N)，πFⅡ=1.50，πC=63，B=9.1。如果不考慮技術限制，單設計點方法的優化結果更好。但實際上，由于單設計點方法的冷卻氣量和爬升末端T4不隨πC和πFⅡ變化，這樣會造成一部分設計域不滿足要求。

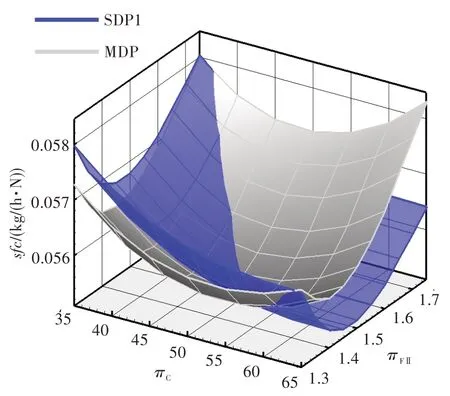
圖1 多設計點方法算例與單設計點方法算例1 的巡航耗油率對比Fig.1 Specific fuel consumption at cruise of MDP and SDP1

圖2 為兩種算例的起飛推力隨πC和πFⅡ的變化。由圖可知，多設計點方法算例的起飛推力保持為330 kN，而單設計點方法算例1 的起飛推力隨πC和πFⅡ變化，變化范圍為315～360 kN。發動機起飛狀態的性能需求為推力330 kN，只有起飛推力大于330 kN 的區域才滿足要求，即兩個曲面的交線就是單設計點方法算例1 推力可行域的邊界，推力在邊界之下的區域為不可行域。

圖2 多設計點方法算例和單設計點方法算例1 的起飛推力對比Fig.2 Thrust at TO of MDP and SDP1

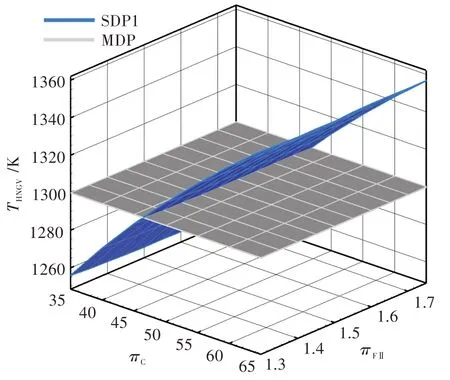
圖3 多設計點方法算例和單設計點方法算例1 的高壓渦輪導向器金屬溫度對比Fig.3 Metal temperature of high pressure turbine nozzle guide vane of MDP and SDP1

圖3 為兩種算法的高壓渦輪導向器金屬溫度對比。類似于起飛推力，多設計點方法算例的高壓渦輪導向器金屬溫度嚴格等于1 300 K，單設計點方法算例1 的高壓渦輪導向器金屬溫度隨πC的增加而升高，且變化范圍為1 240～1 340 K。高壓渦輪導向器最高允許金屬溫度為1 300 K，只有低于1 300 K 的區域才滿足技術限制，即兩個曲面的交線就是單設計點方法算例1 溫度可行域的邊界，在邊界之上的區域為不可行域。

綜合分析圖2 和圖3 可看出：多設計點方法的結果總是嚴格滿足性能需求和技術限制；單設計點方法所得結果，在一部分區域由于推力大于指標要求或是高壓渦輪導向器金屬溫度低于技術限制(使用了過多的冷氣)造成了性能浪費，而另一部分區域由于不滿足推力需求或是超出了高壓渦輪導向器金屬溫度的技術限制造成了設計域的不可行。

在同時考慮性能需求和技術限制的條件下，圖4 給出了單設計點方法算例1 設計域的可行域、溫度邊界和推力邊界。由圖可知：單設計點方法算例1的可行域只占其設計域的很小一部分，溫度邊界為πC≤45，推力邊界與πFⅡ軸的交點為πFⅡ=1.45；耗油率最優點不在可行域內，不滿足設計要求。可行域內的最優耗油率為0.055 9 kg/(h·N)，πFⅡ=1.45，πC=45，B=11。

圖5、圖6 分別示出了多設計點方法算例的爬升末端T4和高壓渦輪導向器冷卻氣量。由圖可看出，爬升末端T4隨πC和πFⅡ變化，且πFⅡ對爬升末端T4的影響較大，爬升末端T4隨著πFⅡ的升高而降低。冷卻氣量也隨πC和πFⅡ變化，且πC對冷卻氣量的影響較大，冷卻氣量隨著πC的增加而增加。這是因為最高T4保持1 850 K 不變，隨著πC的增加，壓氣機出口溫度(冷氣溫度)增加，就必須增加冷卻氣量以保持高壓渦輪導向器金屬溫度不變。

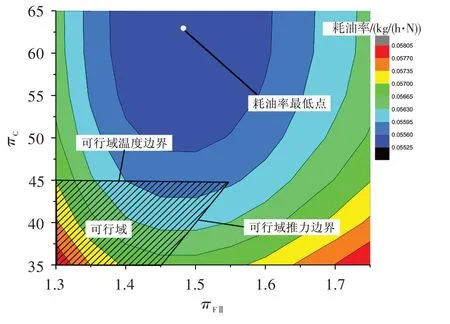
圖4 單設計點方法算例1 的設計域和可行域Fig4 Design space and feasible region of SDP1

圖5 多設計點方法算例的爬升末端燃燒室出口溫度Fig.5 T4at TOC of MDP

圖6 多設計點方法算例的高壓渦輪導向器冷卻氣量Fig.6 High pressure turbine nozzle guide vane cooling flow of MDP

綜上分析可知：單設計點方法假設了冷卻氣量和爬升末端T4保持不變，使設計域的一部分區域造成了性能浪費，而另一部分區域不滿足要求，且性能最優點有可能在不可行域；多設計點方法的冷卻氣量和爬升末端T4為平衡方程組的迭代變量，隨設計變量πC和πFⅡ變化，使得多設計點方法的設計域總是嚴格滿足性能需求和技術限制。

3.3.2 單設計點方法設計參數的調整

單設計點方法算例1 的設計域存在很大一部分區域為不可行域，且耗油率最優點也在不可行域內，需要調整設計點參數以改變設計域邊界。從前文分析可知，總壓比增加使冷卻氣溫度增加，必須增加冷卻氣量才能使高壓渦輪導向器金屬溫度滿足技術限制；隨著風扇壓比的增加，必須降低爬升末端T4才能使起飛推力滿足性能需求。為此，在單設計點方法算例1 的基礎上，單設計點方法算例2(SDP2)增加了冷卻氣量、降低了爬升末端T4(表6)，以增加設計域的可行域，除此之外，兩個算例的其他設置完全相同。

表6 單設計點方法算例2 的設計點參數設置Table 6 Parameters for SDP2 of single design point method

圖7、圖8 分別為多設計點方法算例與單設計點方法算例的起飛推力和高壓渦輪導向器金屬溫度的對比。由圖可知，單設計點方法算例2 的推力比單設計點方法算例1 的高，金屬溫度則比單設計點方法算例1 的低。這表明增大冷卻氣量并減小爬升末端T4，可以增加設計域的可行域范圍。

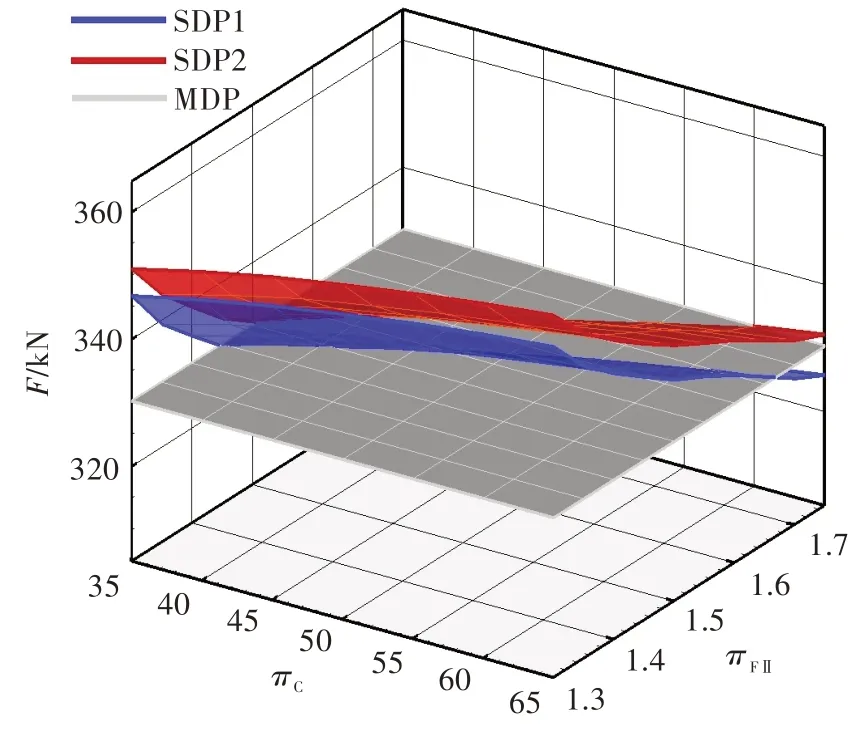
圖7 多設計點方法算例和單設計點方法算例的起飛推力對比Fig.7 Thrust at TO of MDP,SDP1,SDP2

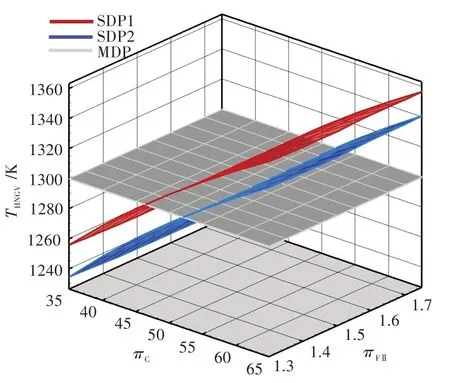
圖8 多設計點方法算例和單設計點方法算例的高壓渦輪導向器金屬溫度的對比Fig.8 High pressure turbine nozzle guide vane metal temperature of MDP,SDP1,SDP2

圖9 為多設計點方法算例和單設計點方法算例的巡航耗油率對比。從圖中可看出，多設計點方法算例和單設計點方法算例1、算例2 的設計域分別相交，但單設計點方法算例1 和算例2 并沒有交線。對應于每個πC和πFⅡ的組合，單設計點方法算例2 的耗油率都比單設計點方法算例1 的高。

圖10 示出了單設計點方法算例2 設計域的可行域。對比圖4 可看出，單設計點方法算例2 的可行域明顯增大，溫度邊界為πC≤50，推力邊界與πFⅡ軸的交點為πFⅡ=1.5，但耗油率最優點依然不在可行域內。

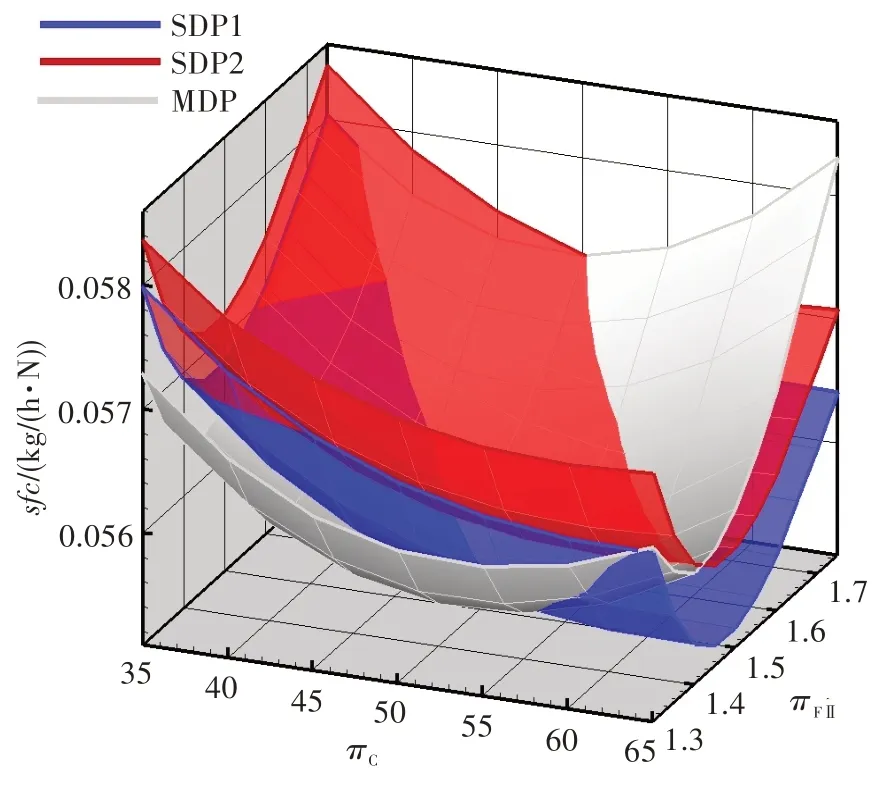
圖9 多設計點方法算例和單設計點方法算例的巡航耗油率對比Fig.9 Specific fuel consumption at cruise of MDP,SDP1,SDP2

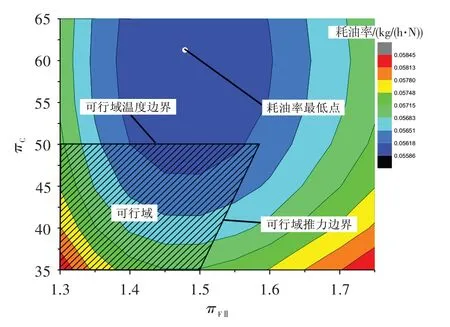
圖10 單設計點方法算例2 的設計域及可行域Fig.10 Design space and feasible region of SDP2

綜合分析圖9、圖10 可知：單設計點方法算例2由于降低了爬升末端的T4，增加了冷卻氣量，使得起飛推力比單設計點方法算例1 的大，高壓渦輪導向器金屬溫度比單設計點方法算例1 的低，可行域范圍增大；但是也由于冷氣量的增加，在增大可行域范圍的同時，使得巡航耗油率整體升高，最優耗油率約為0.551 kg/(h·N)，優化結果反而變差，此時單設計點方法算例2 的耗油率最優點仍不在可行域內，若繼續增大其可行域的邊界，可以預見優化結果會繼續惡化；如果減小冷卻氣量使耗油率整體降低，又會使可行域范圍減小。由此看出，在單設計點方法中，僅通過設計人員主觀調整，很難使設計域既滿足所有技術限制和性能需求，又不造成性能浪費。

4 結論

針對航空發動機的熱力循環分析過程提出了一種同時考慮多個設計點需求的實現方法，并詳細介紹了其構建、求解過程。通過對比、分析表明，多設計點方法可以自動調整循環參數（文中為爬升末端燃燒室出口溫度和高壓渦輪導向器冷卻氣流量），使設計域總是滿足技術限制和性能需求，確保航空發動機熱力循環分析過程更為準確、高效。