帶權(quán)決策表的變精度約簡算法

李 旭,榮梓景

(北京語言大學(xué) 信息科學(xué)學(xué)院,北京 100083)E-mail:1165297698@qq.com

1 引 言

粗糙集理論[1]是由波蘭學(xué)者Pawlak提出的,是一種處理不確定、不一致和模糊問題的數(shù)學(xué)分析工具.近年來,粗糙集理論的研究成果豐碩,在機(jī)器學(xué)習(xí)、數(shù)據(jù)挖掘、決策支持與分析、醫(yī)療衛(wèi)生服務(wù)、物聯(lián)網(wǎng)等諸多領(lǐng)域中,取得了成功的應(yīng)用.由于經(jīng)典的粗糙集對分類誤差敏感,使其應(yīng)用受到了很大程度的限制而降低了分類預(yù)測能力.為了克服經(jīng)典粗糙集模型的這種局限性,變精度模型[2]引入概率后,增強(qiáng)了模型的抗噪性,可以更有效得處理數(shù)據(jù)分類,因而推進(jìn)了粗糙集理論的研究,并且拓寬了粗糙集理論的應(yīng)用領(lǐng)域.

屬性約簡是粗糙集理論研究的重要內(nèi)容,其主要思想就是根據(jù)特定規(guī)則要求,刪除冗余和不相關(guān)屬性,構(gòu)成知識(shí)分類最小屬性集.許多學(xué)者對正區(qū)域約簡、變精度粗糙集模型進(jìn)行了深入研究,在經(jīng)典粗糙集模型約簡中,二元關(guān)系是等價(jià)關(guān)系,為了更好處理信息丟失的決策表,已有研究通過容差關(guān)系[3]、相似關(guān)系[4]、量化容差關(guān)系[5]、限制容差關(guān)系[6]拓展了粗糙集約簡研究.目前,Liu[7]在一致決策表和不一致決策表上提出了一般關(guān)系,從而推廣了決策表中的二元關(guān)系,并研究了關(guān)系決策系統(tǒng)上的屬性約簡.文獻(xiàn)[8]用一般關(guān)系給出了正區(qū)域約簡的概念及相應(yīng)的辨識(shí)矩陣,并給出嚴(yán)格證明.文獻(xiàn)[9]在變精度模型下討論了7種不同形式的約簡,進(jìn)一步闡述了變精度模型和經(jīng)典粗糙集模型的差異.文獻(xiàn)[10]通過概括了變精度模型的定義,同時(shí),以矩陣的觀點(diǎn)提出了變精度模型的上下近似.文獻(xiàn)[11]中,當(dāng)決策屬性滿足自反性時(shí),證明了關(guān)系決策系統(tǒng)的分布約簡等于關(guān)系系統(tǒng)的約簡.文獻(xiàn)[12]通過計(jì)算條件屬性的重要度,運(yùn)用啟發(fā)式算法得到屬性約簡.文獻(xiàn)[13,14]給出了變精度約簡模型中分布約簡、最大分布約簡和分配約簡的概念,以及所對應(yīng)的辨識(shí)矩陣,并給出了辨識(shí)矩陣的嚴(yán)格證明.文獻(xiàn)[15]提出了變精度約簡中局部約簡的概念,以及對應(yīng)的辨識(shí)矩陣,并給出了嚴(yán)格證明.文獻(xiàn)[16]在變精度模型下,研究參數(shù)的關(guān)系對于對象分類的影響.文獻(xiàn)[17]基于矩陣觀點(diǎn),提出了絕對約簡、分布約簡、正區(qū)域約簡這三種約簡統(tǒng)一的不變矩陣的概念.通過建立不變矩陣統(tǒng)一約簡算法來處理三種不同的約簡.此外,研究人員還提出了不同類型的屬性約簡.例如,覆蓋約簡[18,19]、代價(jià)敏感度約簡[20].現(xiàn)有屬性約簡研究主要針對不同背景的實(shí)際問題,對粗糙集進(jìn)行屬性約簡,而缺少對于不同屬性約簡之間相互聯(lián)系的研究.由于變精度約簡和正區(qū)域約簡是決策表中兩種重要的約簡類型.因此,研究變精度約簡和正區(qū)域約簡之間的聯(lián)系是有意義的.

本文提出了帶權(quán)決策表的概念并研究了帶權(quán)決策表中變精度約簡方法.在帶權(quán)決策表中,通過對變精度約簡和正區(qū)域約簡進(jìn)一步比較研究中,當(dāng)精度閾值大于0.5時(shí),給出了一種經(jīng)適當(dāng)更改部分對象的決策值后得到新的決策表的具體方法,該方法雖然使得原有的決策規(guī)則發(fā)生改變,但此時(shí),帶權(quán)決策表中的變精度約簡可以轉(zhuǎn)化為新的決策表中的正區(qū)域約簡,并給出了兩者對應(yīng)的辨識(shí)矩陣等價(jià)證明,從而提出了一種關(guān)于變精度約簡轉(zhuǎn)化為正區(qū)域約簡的具體算法.本文所提出的算法簡化了原來的計(jì)算過程.

本文結(jié)構(gòu)組織如下:第2節(jié)回顧了粗糙集中的基本概念、正區(qū)域約簡定義及其對應(yīng)的辨識(shí)矩陣.第3節(jié)提出了帶權(quán)的決策表模型,給出了帶權(quán)決策表中的變精度約簡及其相應(yīng)的辨識(shí)矩陣.第4節(jié),當(dāng)精度閾值大于0.5時(shí),提出了一種變精度約簡轉(zhuǎn)化為正區(qū)域約簡的具體轉(zhuǎn)化算法,并給出了理論證明.第5節(jié)通過舉例分驗(yàn)證了算法的有效性.

2 基本概念

本節(jié)主要回顧了正區(qū)域約簡以及其對應(yīng)的辨識(shí)矩陣.屬性約簡主要是通過辨識(shí)矩陣算法或者啟發(fā)式算法實(shí)現(xiàn)的,啟發(fā)式算法雖然能夠得到約簡,但往往不能得到所有約簡.基于辨識(shí)矩陣的約簡方法的數(shù)學(xué)論證嚴(yán)格,能夠得到所有約簡,目前仍是得到所有約簡的最好方法.因此,本文所涉及的屬性約簡是在辨識(shí)矩陣[21,22]的基礎(chǔ)上實(shí)現(xiàn)的,通過得到辨識(shí)函數(shù),將其從合取范式轉(zhuǎn)換為析取范式,從而得到全部約簡.

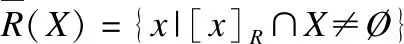
定義3.若X?U,對于?x∈U,定義關(guān)于X的特征函數(shù)[7]λX(x)為:

(1)

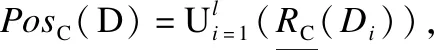
1)PosC(D)=PosB(D)Δ

(2)

2)若?≠B′?C,PosC(D)≠PosB′(D)

(3)

稱B是C關(guān)于D的正區(qū)域約簡.

在計(jì)算正區(qū)域約簡時(shí),相應(yīng)的辨識(shí)矩陣[8]為M=(mij)s×n:

(4)

在辨識(shí)矩陣M中,s=|PosC(D)|是正區(qū)域的基,n=|U|是論域中的元素?cái)?shù).

3 帶權(quán)決策表的變精度約簡

在決策表的基礎(chǔ)上,通過引入權(quán),本節(jié)提出了帶權(quán)的決策表的概念,因而帶權(quán)的決策表是對通常決策表概念的推廣.并在帶權(quán)決策表中,提出了變精度約簡及其對應(yīng)的辨識(shí)矩陣.

3.1 帶權(quán)的決策表

在決策表中,若把決策表中的每一行作為一條決策規(guī)則,對于出現(xiàn)相同決策規(guī)則的次數(shù)稱為權(quán).本文假設(shè)所有的權(quán)值為正整數(shù).這時(shí)給決策表增加一列來表示權(quán),使得決策規(guī)則在決策表中出現(xiàn)的次數(shù)由權(quán)來表示,則稱該決策表稱為帶權(quán)的決策表,用(U,C∪D,W)表示,其中,U是論域,C是條件屬性集,D是決策屬性集,W為對象的權(quán),RC,RD分別是條件屬性,決策屬性在U上的等價(jià)關(guān)系.

例如,決策表(U,C∪D)(表1),其中,對象集U={ui|i=1,2,…,8},條件屬性集C={a1,a2,a3},D是決策屬性集.

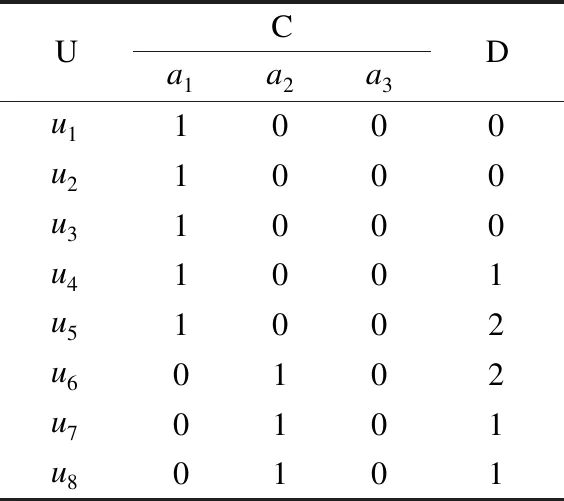
表1 決策表Table 1 Decision table

例如,在條件等價(jià)類{u1,u2,u3,u4,u5}中,對象u1,u2,u3具有相同的決策規(guī)則,且該條規(guī)則共出現(xiàn)3次,我們給這條規(guī)則的權(quán)值賦為3.對象u4僅有1條決策規(guī)則,我們給這條規(guī)則的權(quán)值賦為1,對象u5僅有1條決策規(guī)則,我們給這條規(guī)則的權(quán)值賦為1.現(xiàn)對決策表(表1)增加權(quán)后,得到了帶權(quán)的決策表(U,C∪D,W)(表2),其中,對象集U={xi|i=1,2,…,5},W為對象的權(quán).

定義5.設(shè)(U,C∪D,W)為帶權(quán)的決策表(定義同上),條件屬性決定的等價(jià)類記為[x]C,當(dāng)X?U時(shí),定義:

(5)

定義6.設(shè)(U,C∪D,W)為帶權(quán)的決策表(定義同上),條件屬性決定的等價(jià)類記為[x]C,決策屬性所確定的商集為U/D={D1,D2,…,Dl},對于?x∈U,則記向量[10]為:

(6)

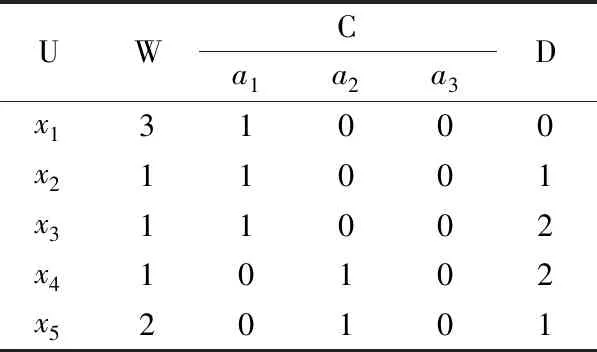
表2 帶權(quán)的決策表Table 2 Weighted decision table

屬性重要度[1,13]是衡量條件屬性相對于決策屬性依賴程度的度量指標(biāo),一般情況下,不同條件屬性的重要度是不同的,條件屬性的重要度越大,說明該條件屬性相對于決策屬性越重要,計(jì)算屬性重要度對于條件屬性具有重要意義,因此,我們基于帶權(quán)的決策表提出了屬性重要度.

定義7.設(shè)(U,C∪D,W)為帶權(quán)的決策表(定義同上),x∈U,對于條件屬性a∈C,其屬性重要度為:

(7)

在帶權(quán)的決策表中,條件屬性重要度越大,說明該條件屬性對正區(qū)域影響作用較大,反之,說明該條件屬性對正區(qū)域影響作用較小.

3.2 帶權(quán)決策表的變精度約簡

在帶權(quán)的決策表模型中,結(jié)合變精度約簡[10,15],可以得到變精度約簡對應(yīng)的辨識(shí)矩陣.相比于決策表中的變精度約簡對應(yīng)的辨識(shí)矩陣,定義向量μCD(x)側(cè)重于考慮條件類的元素個(gè)數(shù).而在帶權(quán)的決策表中,變精度約簡對應(yīng)的辨識(shí)矩陣,定義向量μCD(x)側(cè)重于考慮條件類中元素的權(quán)值.

引理1.設(shè)(U,C∪D,W)為帶權(quán)的決策表(定義同上),決策屬性所確定的商集為U/D={D1,D2,…,Dl},當(dāng)β∈[0,1]時(shí),對于任意x∈U,μCD(x)的β截向量[15]如下:

(μCD(x))β=(λ(RC)(β)(D1),λ(RC)(β)(D2),…,

λ(RC)(β)(Dl))

(8)

引理2.設(shè)(U,C∪D,W)為帶權(quán)的決策表(定義同上),當(dāng)β∈[0,1]時(shí),對于任意x∈U,μCD(x)的β截向量[15]如下:

(9)

定義8.設(shè)(U,C∪D,W)為帶權(quán)的決策表(定義同上),?≠B?C,若B滿足下列兩條件:

1)對于?x∈U,(μCD(x))β=(μBD(x))β

(10)

2)若?≠B′?B,?x∈U,有(μCD(x))β≠(μB′D(x))β

(11)

稱B是精度閾值為β的變精度約簡[15,17].

(12)

其中,在辨識(shí)矩陣M(β)中,n=|U|表示論域中的元素?cái)?shù).由公式(12)知,對于任意精度閾值β1,β2,其相應(yīng)所得的約簡結(jié)果可能不相同.

1)(μCD(x))β=(μBD(x))β

(13)

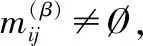
(14)

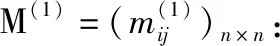
(15)

在帶權(quán)的決策表中,精度閾值為1的變精度約簡對應(yīng)的辨識(shí)矩陣和正區(qū)域約簡對應(yīng)的辨識(shí)矩陣等價(jià)[17],因而可得相同約簡.

4 帶權(quán)決策表的變精度約簡與正區(qū)域約簡

相比正區(qū)域約簡,變精度約簡計(jì)算過程相對復(fù)雜.當(dāng)精度閾值β大于0.5時(shí),我們發(fā)現(xiàn)變精度約簡可以轉(zhuǎn)化為正區(qū)域約簡進(jìn)行計(jì)算.因而本節(jié)提出了在帶權(quán)決策表上更改某些(個(gè))等價(jià)類[x]C中部分對象決策值的具體方法,從而得到新決策表(該定義由4.1節(jié)知).同時(shí),證明了在帶權(quán)決策表中的變精度約簡等于新決策表中的正區(qū)域約簡.

4.1 帶權(quán)的決策表轉(zhuǎn)化過程

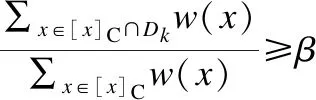
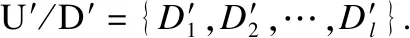
在新的帶權(quán)決策表(U′,C∪D′,W′)中,條件屬性在U′上的等價(jià)關(guān)系不變,但改變了部分對象的決策值,使得決策屬性在U′上的等價(jià)關(guān)系發(fā)生了改變.因此,相比于帶權(quán)的決策表,新的帶權(quán)決策表中不同的決策規(guī)則數(shù)量減少了,則對象的權(quán)值也隨之發(fā)生改變.

例如,(U,C∪D,W)(表3)是帶權(quán)的決策表,U={xi|i=1,2,…,7},條件屬性集C={a1,a2,a3},決策屬性集D,W為對象的權(quán).現(xiàn)取精度閾值β=0.6.

表3 帶權(quán)的決策表Table 3 Weighted decision table

表4 新的帶權(quán)決策表Table 4 New weighted decision table

顯然,當(dāng)任意條件等價(jià)類中所有對象具有相同決策規(guī)則時(shí),即在新的帶權(quán)決策表中,任意條件等價(jià)類僅有一條決策規(guī)則時(shí),該類屬于正區(qū)域集合.反之,任意條件等價(jià)類有兩條及以上的決策規(guī)則時(shí),該類不屬于正區(qū)域集合.

由第2節(jié)所給的正區(qū)域約簡對應(yīng)的辨識(shí)矩陣可知,正區(qū)域約簡時(shí),新的帶權(quán)決策表中的權(quán)不起作用,因此可以刪除對象的權(quán),得到新的決策表(U′,C∪D′)(表5).

表5 新決策表Table 5 New decision table

本文要求精度閾值β大于0.5,主要考慮兩個(gè)方面:閾值取值越大時(shí),雖然提取規(guī)則的確定性越強(qiáng),但容錯(cuò)性也越低.當(dāng)精度閾值小于等于0.5時(shí),一般認(rèn)為是不可信的;若任意條件類的精度閾值β均小于等于0.5時(shí),會(huì)出現(xiàn)多個(gè)決策值滿足要求,則本節(jié)所提出的轉(zhuǎn)化過程無法改變決策值,因而4.2節(jié)中定理2不成立.為保持一定程度的規(guī)則可信度和容錯(cuò)性,精度閾值的取值須大于0.5.例如,(U,C∪D,W)(表6)是帶權(quán)的決策表,U={xi|i=1,2,…,5},條件屬性集C={a1,a2,a3},決策屬性集D,W為對象的權(quán).

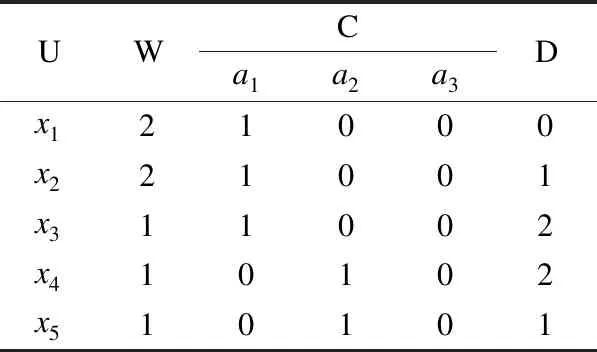
表6 帶權(quán)的決策表Table 6 Weighted decision table

由表6知,商集U/C={{x1,x2,x3},{x4,x5}},商集U/D={D1,D2,D3},其中,D1={x1},D2={x2,x5},D3={x3,x4}.若取精度閾值β=0.3時(shí),在條件類[x1]C={x1,x2,x3}中,該類中有P(D1|[x1]C)=0.4≥β,P(D2|[x1]C)=0.4≥β,按照本節(jié)提出的轉(zhuǎn)化方法,無法改變條件類[x1]C中任意對象的決策值;在條件類[x4]C={x4,x5}中,該類中有P(D2|[x4]C)=0.5≥β,P(D3|[x4]C)=0.5≥β,按照本節(jié)提出的轉(zhuǎn)化方法,無法改變條件類[x4]C中任意對象的決策值;則表6中的正區(qū)域是空集,表6的變精度約簡不能轉(zhuǎn)化成正區(qū)域約簡進(jìn)行計(jì)算.所以需令精度閾值大于0.5.

4.2 帶權(quán)的決策表中變精度約簡與正區(qū)域約簡的關(guān)系

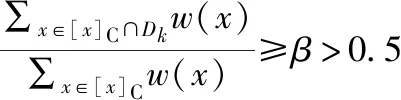
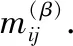
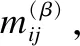
由3.2節(jié)知,辨識(shí)矩陣(4)和辨識(shí)矩陣(15)是正區(qū)域約簡的兩種等價(jià)的形式,其中,辨識(shí)矩陣(4)計(jì)算正區(qū)域約簡時(shí)不需要考慮決策表的權(quán).因此,由定理2知,在帶權(quán)的決策表(U,C∪D,W)中,當(dāng)精度閾值大于0.5時(shí),變精度約簡對應(yīng)的辨識(shí)矩陣等價(jià)于新決策表(U′,C∪D′)中正區(qū)域約簡的辨識(shí)矩陣(4),因而可得相同約簡.本文提出算法1.

算法1.帶權(quán)決策表中精度閾值大于0.5的變精度約簡算法

輸入:β∈(0.5,1],帶權(quán)的決策表(U,C∪D,W)

輸出:變精度約簡

2)計(jì)算新的決策表(U′,C∪D′)中的正區(qū)域約簡的辨識(shí)矩陣M=(mij)s×n;

3)構(gòu)造辨識(shí)函數(shù)f=∏(∑mij≠?mij),并把辨識(shí)函數(shù)f從合取范式轉(zhuǎn)化為析取范式的形式;

比較看來,算法1和變精度約簡算法的時(shí)間復(fù)雜度區(qū)別于構(gòu)建辨識(shí)矩陣的過程,其他步驟的時(shí)間復(fù)雜度相同.變精度約簡算法構(gòu)建辨識(shí)矩陣的時(shí)間復(fù)雜度O(|C|×|U|2),而算法1構(gòu)建辨識(shí)矩陣的復(fù)雜度為O((|PosC(D′)|)×|U|×|C|),其中|PosC(D′)|<|U|,因此,算法1在一定程度上優(yōu)化了時(shí)間復(fù)雜度.

5 實(shí)例分析

為了說明本文的算法,分別用變精度約簡(記WVPR算法)和算法1對表3進(jìn)行實(shí)例分析,例如,U={xi|i=1,2,…,7}代表導(dǎo)致不同機(jī)械故障的7種情況,C={a1,a2,a3}分別代表動(dòng)力系統(tǒng)、供電系統(tǒng)、冷卻系統(tǒng),其中,“1”表示系統(tǒng)運(yùn)行正常,“0”表示系統(tǒng)運(yùn)行出現(xiàn)問題;D為決策集表示故障類型,其中,“0”表示故障F1,“1”表示故障F2,“2”表示故障F3;W為機(jī)械出現(xiàn)某種情況時(shí)發(fā)生故障的頻次.

根據(jù)3.2節(jié)給出的辨識(shí)矩陣(12),因在4.1節(jié)中,取精度閾值β=0.6,則其變精度約簡對應(yīng)的7×7辨識(shí)矩陣為:

根據(jù)該7×7的辨識(shí)矩陣,可構(gòu)造其分辨函數(shù)f=(a1+a2)(a1+a2+a3)(a3),通過合取范式為轉(zhuǎn)化為析取范式,可得f=(a1a3)+(a2a3),則約簡為{a1,a3},{a2,a3}.

當(dāng)取精度閾值β=0.6時(shí),因滿足β∈(0.5,1],現(xiàn)用算法1對帶權(quán)的決策表(表3)進(jìn)行約簡.表3經(jīng)過轉(zhuǎn)化后得到新的決策表(U′,C∪D′)(表5),對于條件等價(jià)類{v3,v4}中,對象v3,對象v4有不同的決策規(guī)則,由正區(qū)域定義知,PosC(D′)={v1,v2},根據(jù)公式(4),則正區(qū)域約簡對應(yīng)的2×4辨識(shí)矩陣為:

根據(jù)上述2×4的辨識(shí)矩陣,可構(gòu)造分辨函數(shù)f=(a1+a2)(a1+a2+a3)(a3),通過合取范式為轉(zhuǎn)化為析取范式,可得f=(a1a3)+(a2a3),則約簡為{a1a3},{a2,a3}.

表3中,由辨識(shí)矩陣(12),取精度閾值β=0.65,則其變精度約簡對應(yīng)的7×7辨識(shí)矩陣為:

根據(jù)該7×7的辨識(shí)矩陣,可構(gòu)造其分辨函數(shù)f=(a1+a2)(a3),通過合取范式為轉(zhuǎn)化為析取范式,可得f=(a1a3)+(a2a3),則約簡為{a1,a3},{a2,a3}.

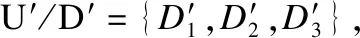
表7 新決策表Table 7 New decision table

PosC(D′)={v4},根據(jù)公式(4),則正區(qū)域約簡對應(yīng)的1×6辨識(shí)矩陣為:

[{a1,a2} ? {a1,a2} ? {a3} {a3}]

根據(jù)上述1×6辨識(shí)矩陣,可構(gòu)造分辨函數(shù)f=(a1+a2)(a3),通過合取范式為轉(zhuǎn)化為析取范式,可得f=(a1a3)+(a2a3),則約簡為{a1,a3},{a2,a3}.

顯然,運(yùn)用兩種算法對決策表進(jìn)行約簡時(shí),所得結(jié)果相同,說明本文的算法是可行的.需要說明的是,不同的精度閾值的變精度約簡得到的約簡可能不同.

表8 數(shù)據(jù)集中的有關(guān)信息Table 8 Relevant information in data sets

為進(jìn)一步說明算法,本文從UCI數(shù)據(jù)集中選取了3個(gè)數(shù)據(jù)集(Wine,Thoracic Surgery,Vehicle Silhouettes)(表8),對WVPR算法和算法1進(jìn)行比較.程序運(yùn)行環(huán)境:Intel(R)Core(TM)i5-2440 CPU 3.10GHz,Windows10 64bits.算法為Python代碼實(shí)現(xiàn).

現(xiàn)取β=0.7時(shí),因?yàn)闈M足β∈(0.5,1]時(shí),精度閾值為0.7的變精度約簡可以轉(zhuǎn)化為正區(qū)域約簡進(jìn)行計(jì)算.表9是兩種算法分別在3個(gè)數(shù)據(jù)集上所得到的約簡,兩種算法所得約簡結(jié)果相同.

表9 兩種算法約簡對比Table 9 Comparisons of two reduction algorithms

表10是算法在不同規(guī)模的數(shù)據(jù)集上運(yùn)行所需的時(shí)間.本文提出的算法運(yùn)行時(shí)間優(yōu)于WVPR算法的運(yùn)行時(shí)間.

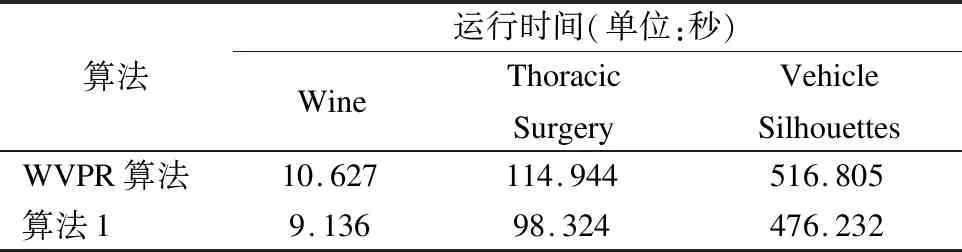
表10 兩種算法約簡時(shí)間Table 10 Reduction time of two algorithms

通過實(shí)驗(yàn)說明:在帶權(quán)的決策表中,當(dāng)變精度約簡的精度閾值β∈(0.5,1]時(shí),可由算法1進(jìn)行計(jì)算,且該算法一定程度上提高了運(yùn)算效率.

粗糙集對通常的決策表進(jìn)行處理時(shí),無需任何先驗(yàn)知識(shí)或信息.帶權(quán)的決策表通過引入權(quán)的概念,為決策表提供了先驗(yàn)知識(shí)或附加信息,因而提出了在該表中的變精度約簡問題.相對于帶權(quán)決策表中的變精度約簡,本文所提算法能夠在更少時(shí)間得到全部約簡.此外,該算法可應(yīng)用在智能診療,事故應(yīng)急決策等領(lǐng)域.

6 結(jié)束語

本文首先在決策表的基礎(chǔ)上,考慮相同決策規(guī)則出現(xiàn)的次數(shù),通過對決策表中的對象賦權(quán)值,提出了帶權(quán)的決策表,并給出了該表中的變精度約簡對應(yīng)的辨識(shí)矩陣.其次,若精度閾值滿足大于0.5的特定條件時(shí),通過改變某些(個(gè))條件類中部分對象的決策值,可得到新的決策表.同時(shí),證明了帶權(quán)決策表中的變精度約簡和新決策表中正區(qū)域約簡相等,從而提出了滿足特定精度閾值時(shí),變精度約簡轉(zhuǎn)化為關(guān)于新決策表中正區(qū)域約簡的具體算法.相較于變精度約簡,本文所提算法能夠在更少時(shí)間得到約簡.最后,通過實(shí)驗(yàn)說明了本文提出算法的可行性和有效性.在之后的工作中,我們將致力于解決非等價(jià)關(guān)系(相似關(guān)系、容差關(guān)系等)基礎(chǔ)上的帶權(quán)決策表中屬性約簡問題.