一種基于模糊劃分和模糊加權的集成深度信念網絡

張雄濤，胡文軍，王士同

（1. 江南大學 數字媒體學院，江蘇 無錫 214122; 2. 湖州師范學院 信息工程學院，浙江 湖州 313000）

近年來，深度學習在圖像識別和語音識別領域取得了突破性的進展。深度學習逐漸成為機器學習最熱的研究方向之一。由于RBM(restricted boltzmann machine)[1-3]具有表達能力強、易于推理等優點被成功用作深度神經網絡的結構單元。當前，以RBM[4-5]為基本構成模塊的DBN(深度信念網絡)、DBM(深度玻爾茲曼機)等模型被認為是最有效的深度學習算法。其中深度信念網絡(DBN)是深度學習的典型代表，通常DBN在進行圖像及語音等模式識別上有較高的精度，但是訓練一個DBN的復雜度非常高，因為DBN在微調階段使用了BP算法，這種算法很難做到多機并行，所以在大規模的數據上進行學習會非常困難。綜上，DBN主要存在兩個問題：1)訓練一個DBN的時間復雜度仍然較高；2)達到好的效果通常需要較多的隱含節點數，然而當隱含節點數較多時又易產生過擬合。雖然鄧力等[6-8]通過改進DBN的網絡結構來提升其性能，但仍然沒有突破以上問題。

分類是深度學習的核心問題，提高分類器的分類性能是分類器研究的主要目標之一。通常將模糊理論與分類器相結合，用于處理不確定問題。在構建分類模型時，為了對所構建的目標模型的局部細節有更好的逼近程度，通常的做法是將輸入空間劃分成多個模糊區域或模糊子空間，即模糊劃分[9-10]，在各個子空間中分別構建分類子模型，最后將各子模型的結果集成輸出[11-12]。有3種模糊劃分方法，即格狀劃分、樹狀劃分和散狀劃分。格狀劃分是將每一維度的輸入空間作劃分，求得其模糊集合，再根據模糊系統理論，將模糊集映射成模糊區域。樹狀劃分是，一次產生一個與模糊區域相對應的一個劃分，每做一次劃分就會產生出劃分面。散狀劃分是，將輸入輸出的數據作分析，將預產生相似結果的輸入空間以模糊區域作劃分，每一模糊區域可作描述輸入輸出數據的行為。該劃分是一種較為靈活的劃分方法，吸收了前兩種方法的優點，同時摒棄了它們存在的不足。在本文的研究中，采用散狀劃分這種方式。

為了更好地挖掘深度模型的表達能力，在實際應用中進一步提高DBN的精度并加快DBN的訓練。受到上述思想的啟發，本文提出了一種基于模糊劃分和模糊加權的集成深度信念網絡，將對應的集成分類算法命名為FE-DBN。首先通過模糊聚類算法FCM將訓練數據劃分為多個子集；然后在各個子集上并行訓練不同結構的DBN；最后借鑒模糊集合理論的思想，將各個分類器的結果進行模糊加權。該算法能夠有效且快速解決大樣本數據的分類問題，克服了單個DBN用于數據分類時時間復雜度較高等缺點；而且，FE-DBN可以避免過擬合問題，具有分類精度高等優點；并在人工數據集、UCI數據集上得到了有效驗證。

1 RBM和DBN

受限玻爾茲曼機是由Hinton和Sejnowski于1986年提出的一種生成式隨機網絡[1]，該網絡是一種基于能量的概率圖模型，它由一個可見層和一個隱含層組成，如圖1所示，v和h分別表示可見層與隱含層，W表示兩層之間的連接權值。對于可見層與隱含層，其連接關系為層間全連接，層內無連接。注意，圖1中h有m個節點，v有n個節點，單個節點用和描述。可見層用于觀測數據，隱含層用于提取特征。RBM的隱單元和可見單元可以為任意的指數族單元。本文只討論所有的可見層和隱含層單元均為伯努利分布，假設所有的可見單元與隱單元均為二值變量，即對。

圖1 RBM示意圖Fig. 1 The structure of RBM

RBM是一種能量模型，能量函數定義為

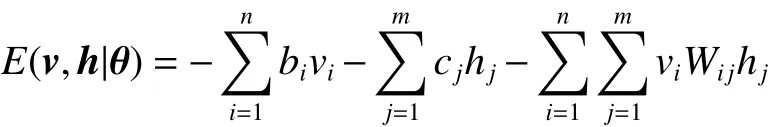
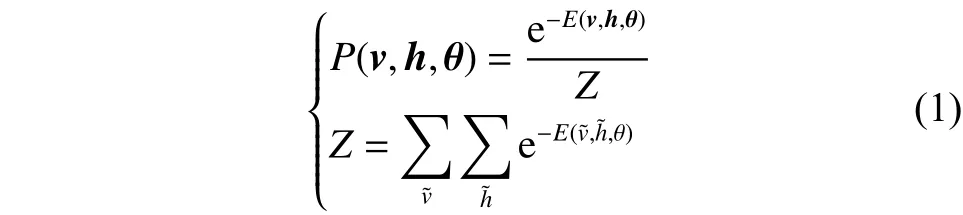
式中Z函數為歸一項。

多個RBM的堆棧組合構成了DBN[5]，前一個RBM的輸出作為后一個RBM的輸入。如圖2所示，最底層是輸入層，最頂層是輸出層，中間層是隱含層。DBN的學習包括兩個階段：預訓練和微調。預訓練是以貪婪的無監督的方式逐層進行訓練的，將輸入層映射到輸出層從而學習到復雜的非線性函數；微調是在監督的方式下實現的，它使用反向傳播(BP)算法從最頂層到最底層對整個DBN網絡參數進行微調。

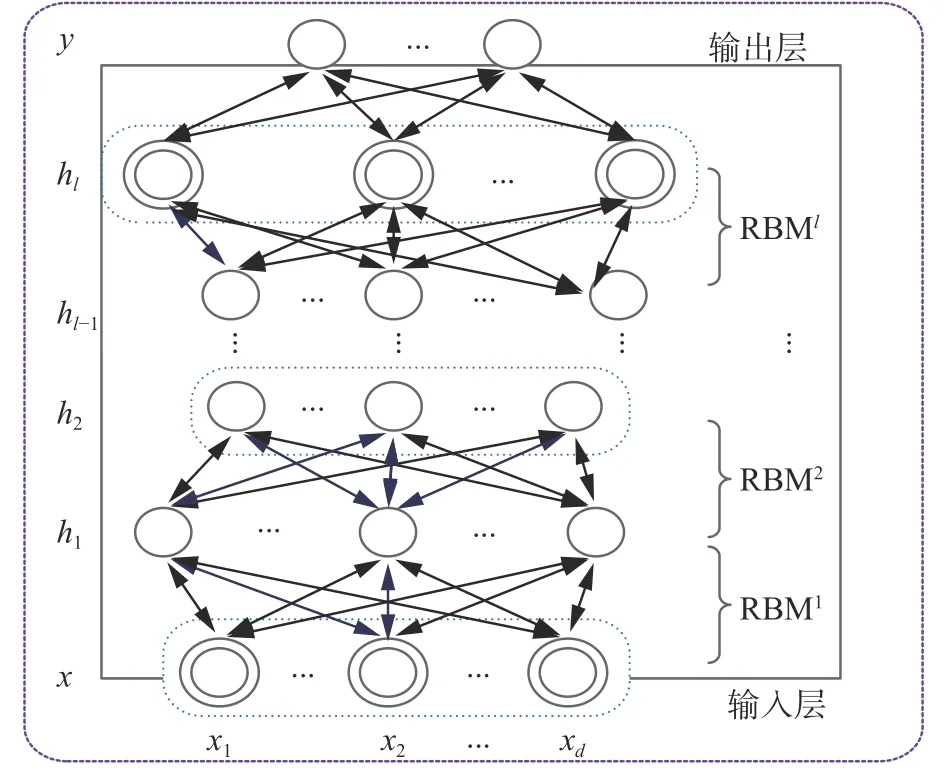
圖2 DBN結構Fig. 2 The structure of DBN

盡管DBN具有強大的知識表達能力，但是當處理大規模數據甚至大數據時，DBN在微調階段需要花費大量的時間去訓練模型，這樣導致訓練時間特別長。

2 基于模糊劃分和模糊加權的DBN分類器集成

針對不同的子空間，從不同的角度來刻畫一個物體各個方面的性質，利用各種不同結構分類器的組合來形成一個綜合的決策。大量的實驗和應用證明：將多個分類器的決策結果按照一定的規則集成在一起，往往可以得到比其中最優分類器還要好的性能[12-15]。針對經典的DBN算法時間復雜度高，容易過擬合，本文將具有多個不同隱含層結構的DBN分類器進行集成，提出了一種基于模糊劃分和模糊加權的集成DBN，即FEDBN。提出的FE-DBN性能優于經典的DBN分類算法，主要有兩個原因：1)在分類之前首先進行預處理、聚類，能夠更好地增強分類精度；2)將訓練集分為多個子集，每個子集用不同結構的DBN訓練，最后將結果進行模糊加權。根據集成學習原理，多個弱分類器的組合能夠組成一個強分類器。

2.1 FE-DBN結構圖

FE-DBN結構圖如圖3所示，首先利用模糊聚類算法FCM，將訓練數據集劃分為K個子集，每個子集分別采用不同結構的DBN模型進行建模(每個DBN子模型中每層隱節點數不一樣，由此構成了K個DBN模型)，各模型獨立并行訓練，最后將各模型所得結果進行模糊加權形成最終輸出。在進行模糊加權時，采用高斯型隸屬度函數進行權值計算。在FE-DBN中，各DBN子模型并行訓練，由于各個訓練子集的數據規模遠遠小于原數據規模，需要較少的隱節點數，因此訓練時間較短。

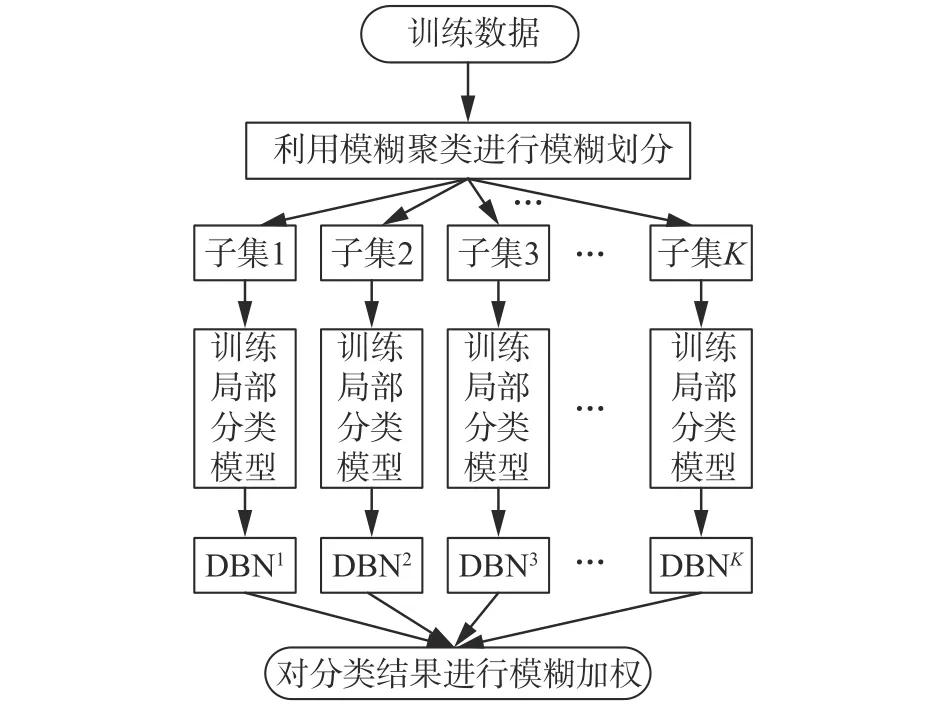
圖3 FE-DBN結構Fig. 3 The structure of FE-DBN

2.2 實現過程

首先，使用模糊聚類算法FCM對訓練數據集進行模糊分組。利用FCM算法進行模糊聚類，FCM的目標函數為[16-19]：

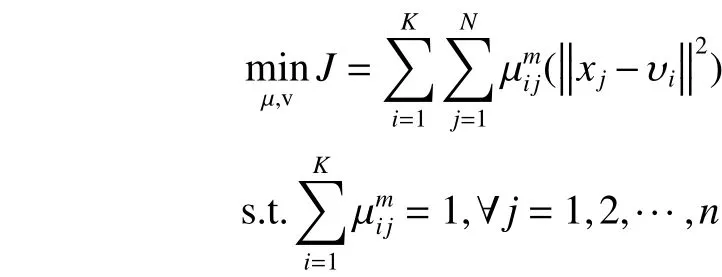
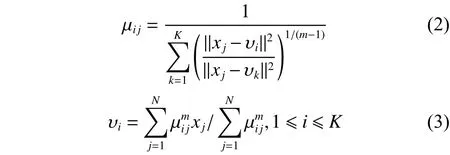
根據式(2)、式(3)，當迭代終止后，所獲得的隸屬矩陣 U 在去模糊化后便得到空間劃分矩陣。

根據式(2)、式(3)，計算寬度為

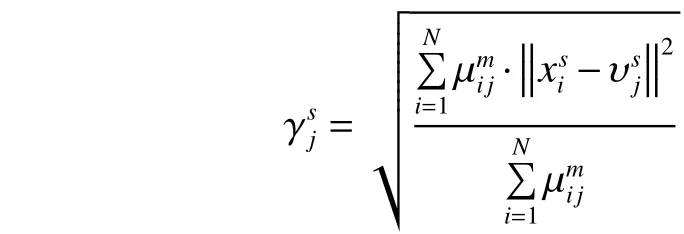
根據聚類中心和寬度的值，并利用式(4)對訓練數據集進行模糊劃分：

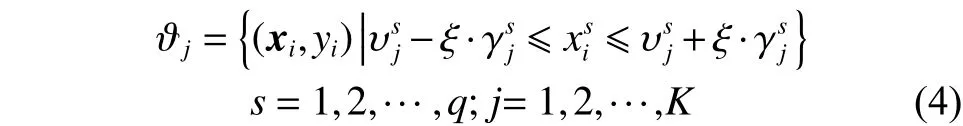
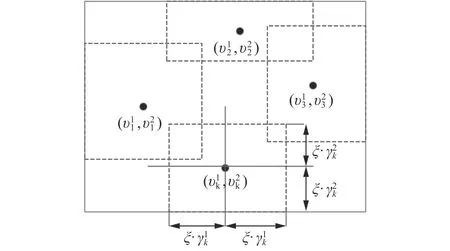
圖4 模糊劃分示意Fig. 4 Fuzzy partition

在式(1)中最關心的是聯合概率分布所確定的邊緣概率分布，由于RBM模型層內無連接，因此當給定可見單元的狀態時，各隱單元的激活狀態是條件獨立的。此時，第j個隱單元的激活概率為

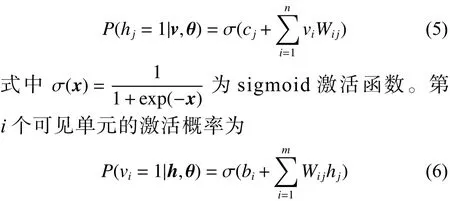
RBM采用Hinton提出的CD-k(對比散度)算法進行參數學習，并證明，當使用訓練樣本初始化時，僅需較少的抽樣步數(一般k=1)就可以得到很好的近似。采用CD-k算法，各參數的更新準則如下[3]：

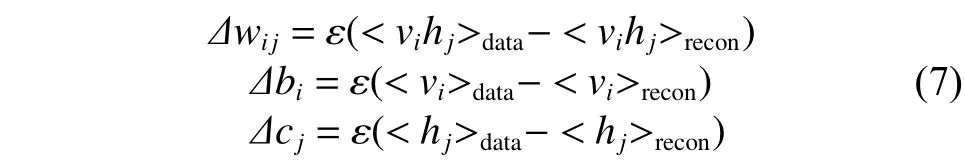
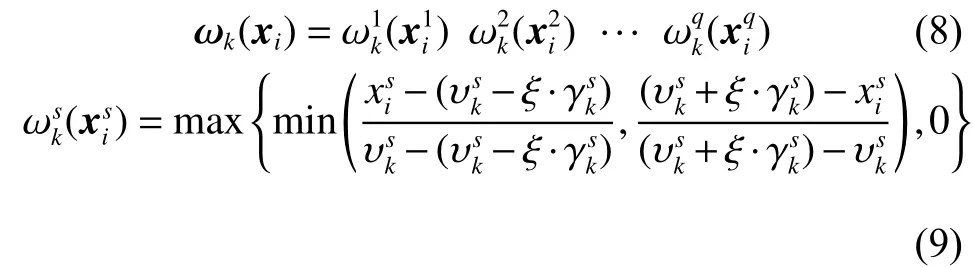
劃分好樣本空間，每一個分類器在樣本子空間進行運算，樣本在分類器中具有局部分類性能最好的，其所對應的權值就越大。

最后，將各DBN分類器所得結果進行模糊加權，即

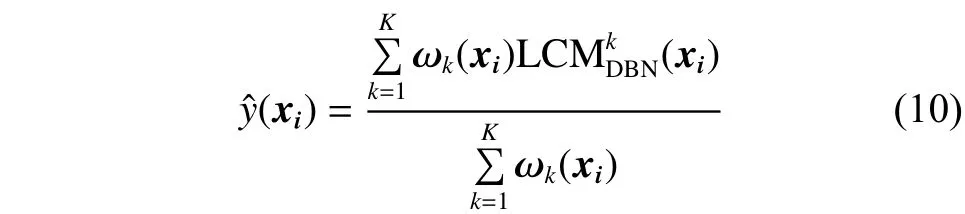
FE-DBN算法實現過程如下：

2)劃分子集。利用模糊聚類算法FCM求得每簇的中心點和寬度，根據式(4)將源數據集劃分為K個子集。

3)并行訓練各子模型DBN1～DBNK，對于所有的可見單元，利用式(5)計算，并抽取且對于所有的隱單元，利用式(6)計算新RBM參數W，b，c的值，即

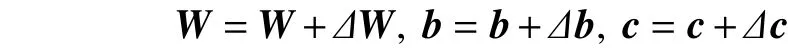
重復3)，直到滿足迭代周期為止。

4)利用式(8)、式(9)計算每個測試數據對各個子集的隸屬度，將測試數據代入3)所得的K個子模型中并輸出K個分類結果。利用式(10)進行集成得到最終輸出。

3 實驗與分析

本文在實驗部分將分別利用人工數據和UCI數據對所提的基于模糊劃分和模糊加權的集成DBN分類算法(FE-DBN)進行驗證和評估。并將該算法的性能同深度信念網絡(DBN)[1-3]算法進行比較。為了驗證本文所提出的算法FE-DBN的有效性，采用的對比算法有局部分類模型DBNK和全局分類模型DBN，其中DBNK表示將原數據集分為K個子集，在每個子集上構建一個局部深度信念網絡分類模型。所有的實驗結果都采用五折交叉，運行10次取均值。

3.1 實驗設置

3.1.1 數據集

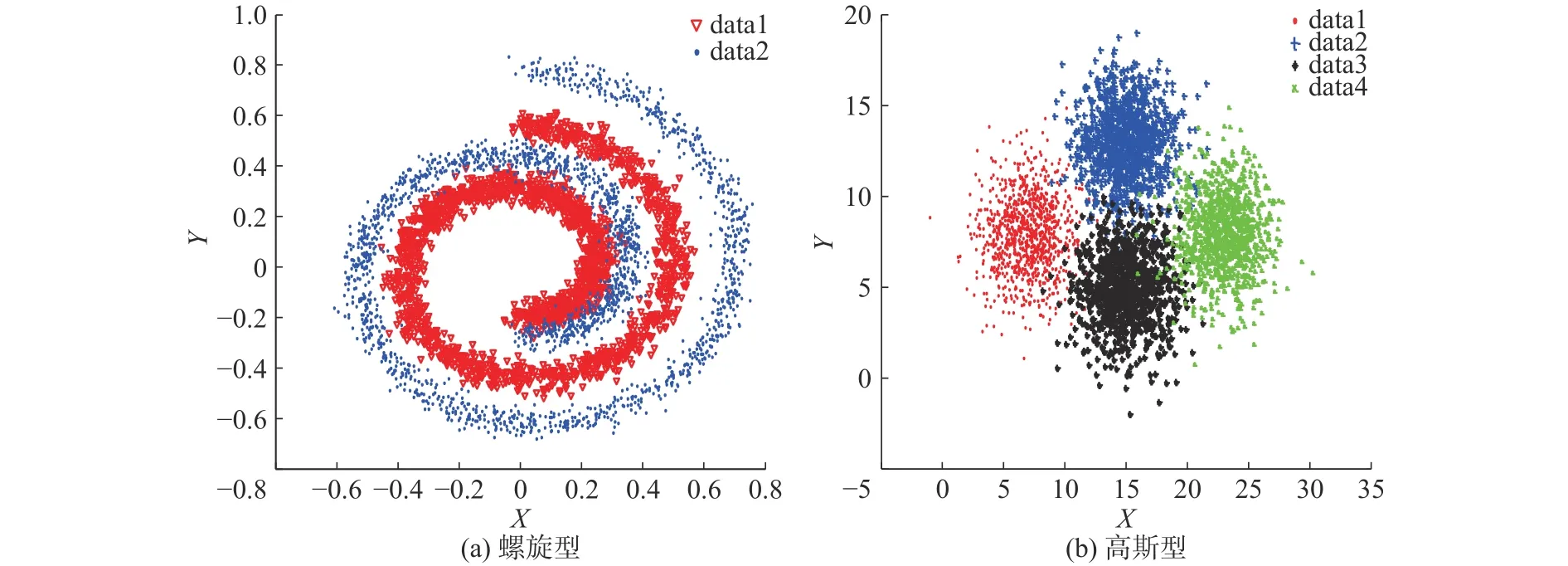
圖5 人工數據集Fig. 5 Artificial datasets

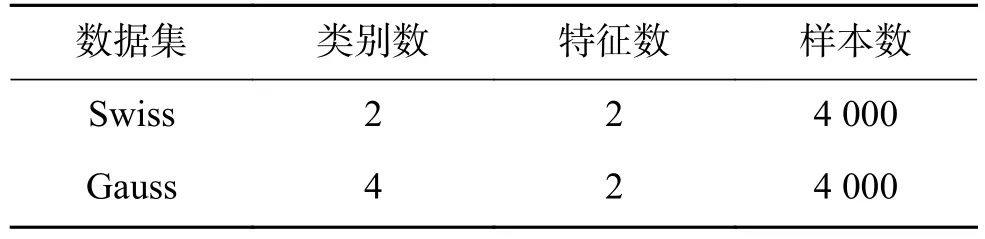
表1 人工數據集Table 1 Artificial datasets

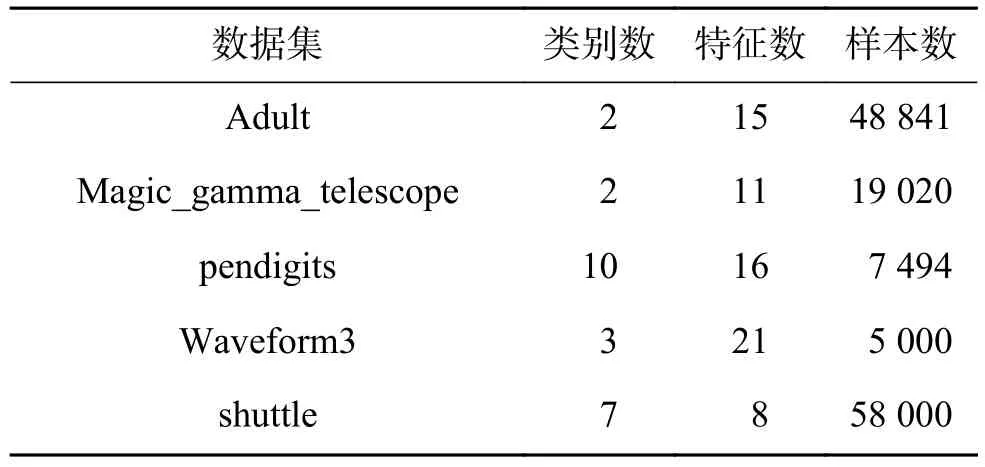
表2 UCI數據集Table 2 UCI datasets

人工數據集生成兩種：左螺旋型、右高斯型，如圖5。兩種數據均生成4 000個樣本，螺旋型2類，2維；高斯型4類，2維。構造的螺旋型數據集正負類樣本數各2 000，高斯型數據集每類樣本數1 000，高斯型各類的中心分別是：[7 8]、[15 13]、[15 5]、[23 8]，協方差均為據集全部來自于UCI[21]。數據集詳細信息如表1、表2所示。調。DBN代碼參照http://www.cs.toronto.edu/～hinton/，RBM迭代周期maxepoch=20，用于控制RBM的預訓練迭代次數和模型參數的微調次數。權重的學習率epsilonw=0.05；顯層偏置的學習率epsilonvb=0.05；隱層偏置的學習率epsilonhb=0.05；權損失系數weightcost=0.000 2；動量學習率 initialmomentum=0.5，finalmomentum=0.9。

本文使用平均測試精度、均方差、運行時間(訓練時間+測試時間)進行算法性能度量。實驗環境為intel(R) Core(TM) i3 3.40 GHz CPU，8 GB內存，Windows10操作系統，MATAB2016a。

3.2 實驗結果及分析

為進一步探索數據集模糊劃分個數對提升分類精度及算法運行時間的重要性，本文將數據集劃分為不同的子集個數，及采用不同的隱節點數組合分別進行實驗比較。如表3所示，局部分類模型DBNK分別有3個子集和4個子集，“28+22+19”表示DBN1中第一層、第二層、第三層的隱節點數分別為28、22、19。

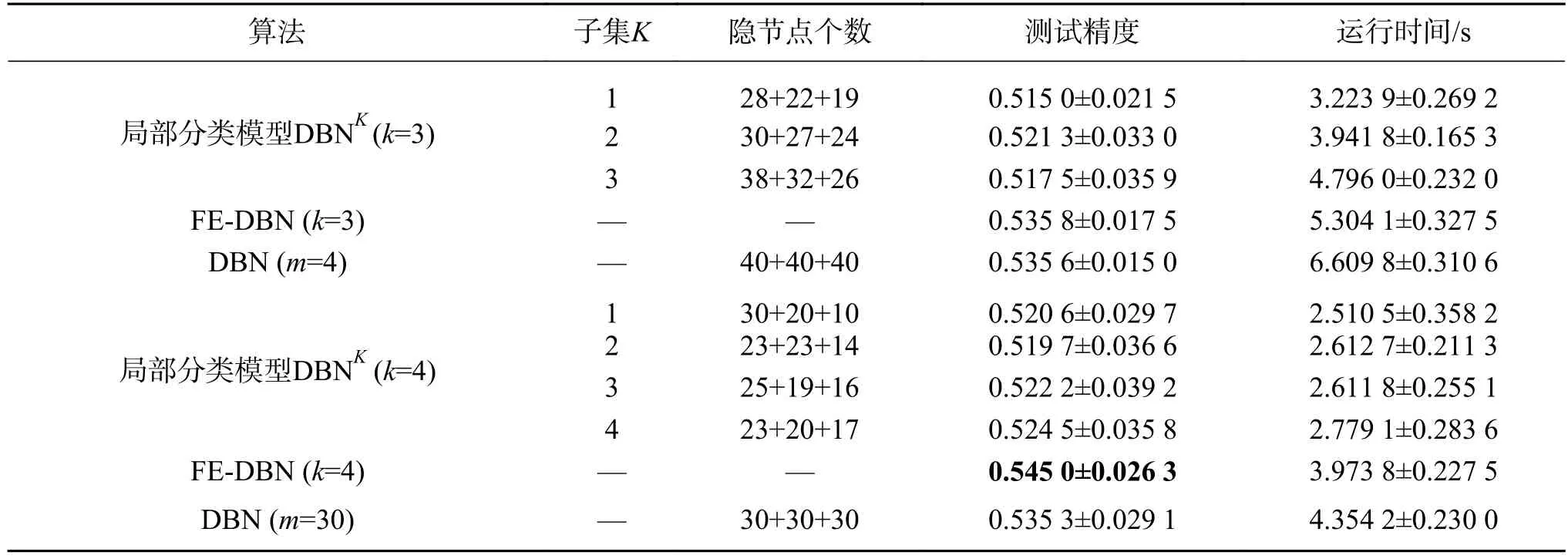
表3 在Swiss數據集上的分類精度及運行時間對比Table 3 Performance in terms of average testing accuracy and running time with their standard deviation on Swiss

3.2.1 人工數據集

該實驗部分主要是通過構造模擬數據集來驗證本文提出的FE-DBN算法的有效性。從表3、表4的實驗結果可以看出：螺旋線數據集不太好區分，精度不高，但是FE-DBN仍有所提升；高斯型數據集精度，FE-DBN比各局部模型DBNK略高，和全局模型DBN基本持平，因為其精度已經很高，故很難再有較大的提升。

表4 在Gauss數據集上的分類精度及運行時間對比Table 4 Performance in terms of average testing accuracy and running time with their standard deviation on Gauss

3.2.2 UCI數據集

本部分實驗選的UCI數據集，既有中等規模數據，又有大規模數據，既有二分類，也有多分類，3種算法在各UCI數據集上的對比實驗結果如表5～9所示。

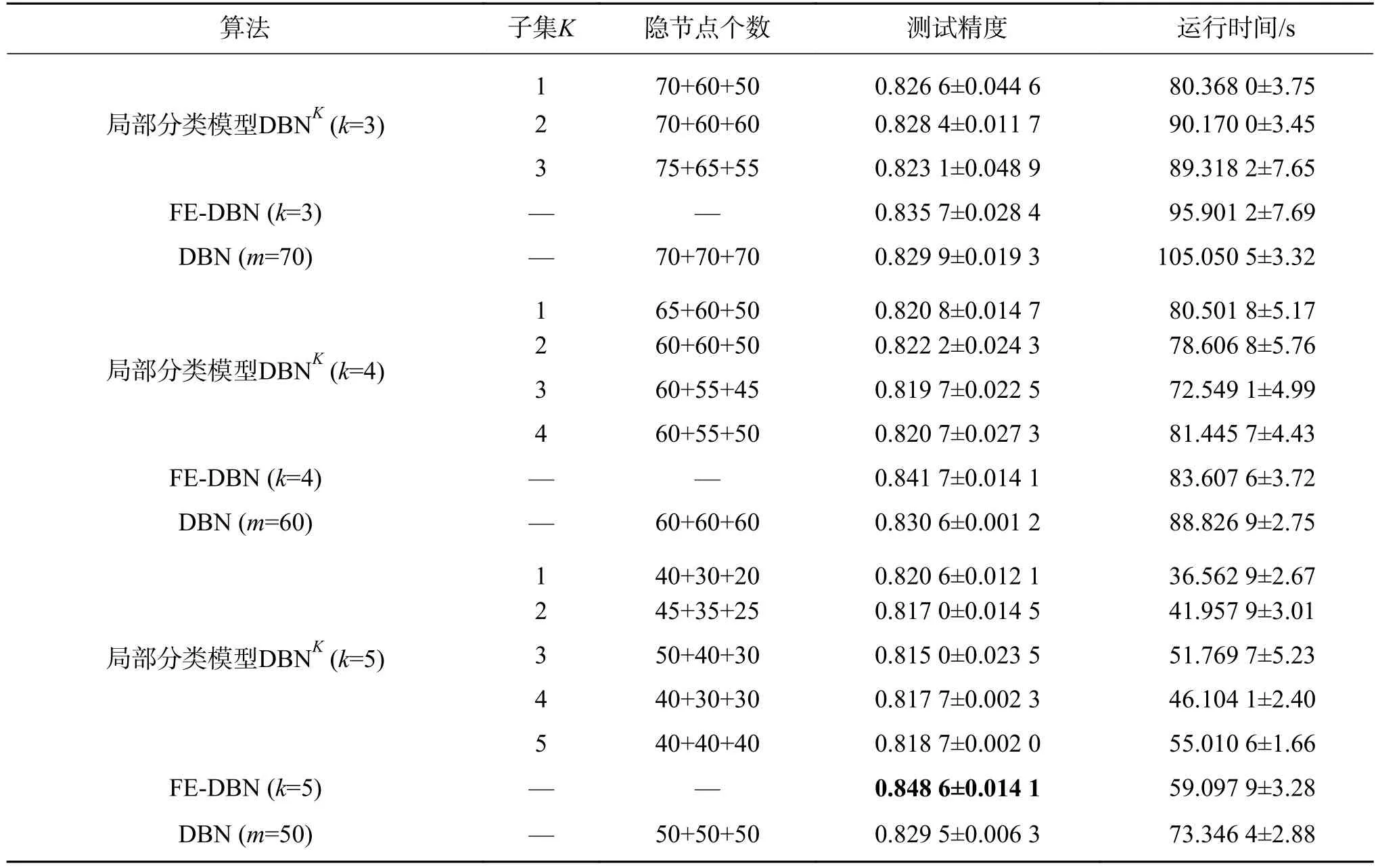
表5 在Adult數據集上的分類精度及運行時間對比Table 5 Performance in terms of average testing accuracy and running time with their standard deviation on Adult

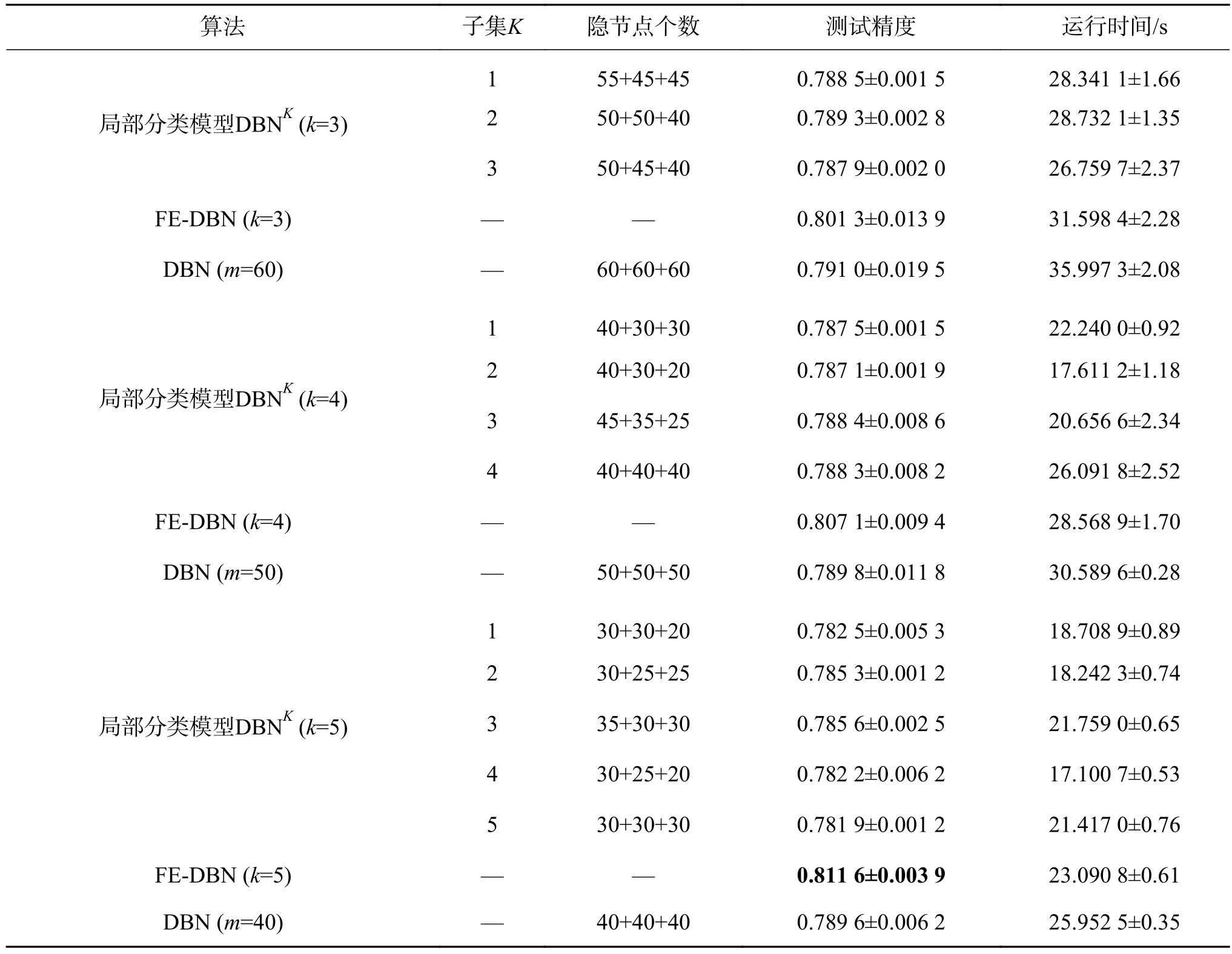
表6 在Magic_gamma_telescope數據集上的分類精度及運行時間對比Table 6 Performance in terms of average testing accuracy and running time with their standard deviation on Magic_gamma_telescope

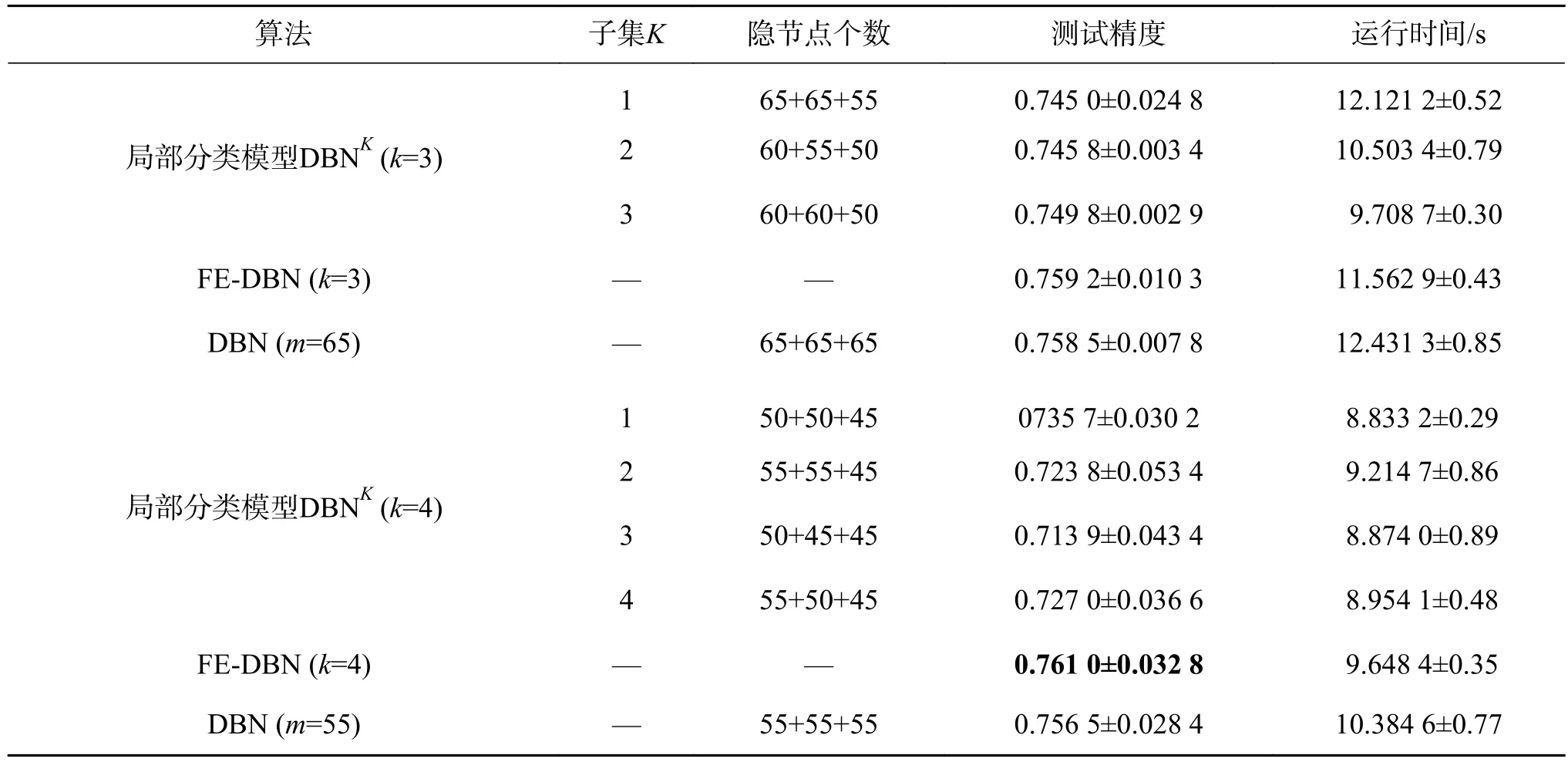
表7 在pendigits數據集上的分類精度及運行時間對比Table 7 Performance in terms of average testing accuracy and running time with their standard deviation on pendigits

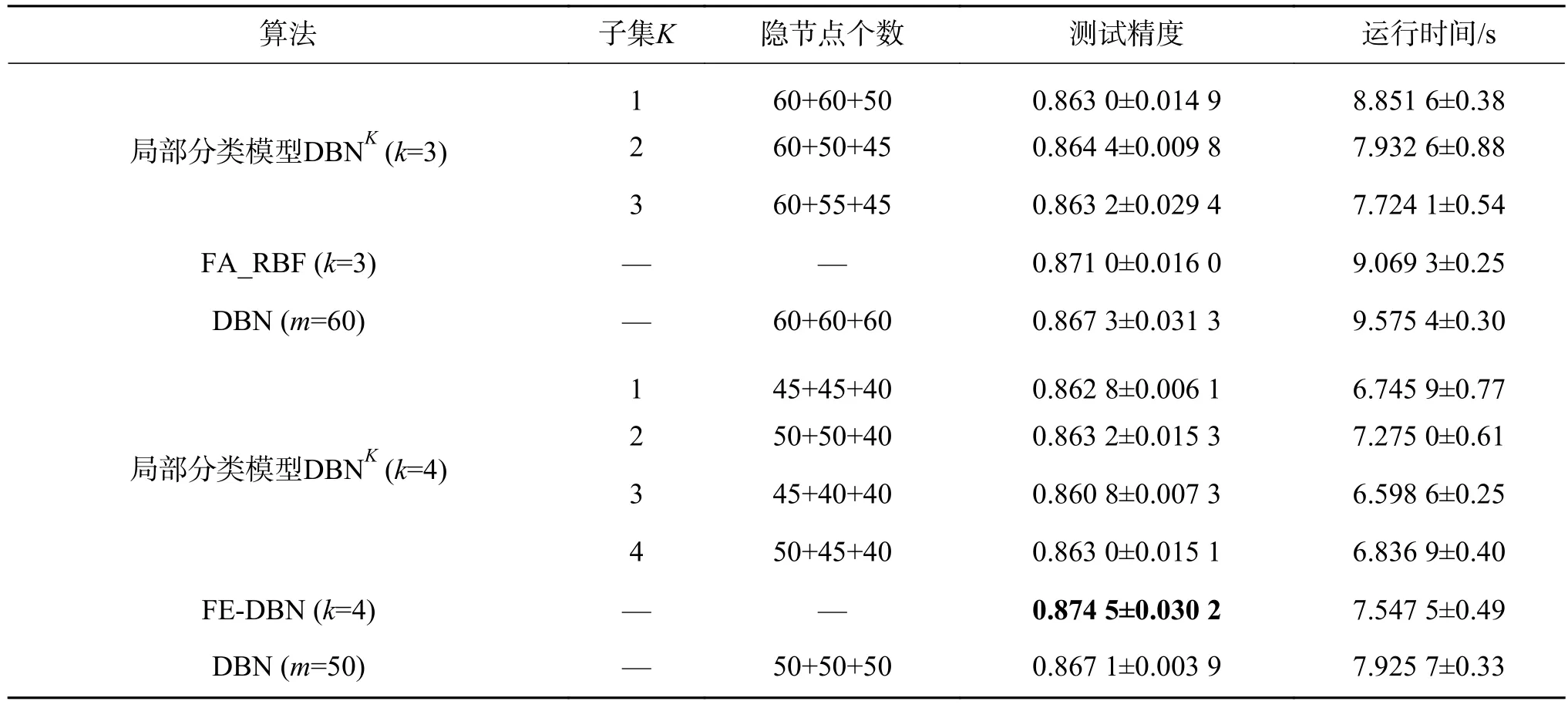
表8 在Waveform3數據集上的分類精度及運行時間Table 8 Performance in terms of average testing accuracy and running time with their standard deviation on Waveform3

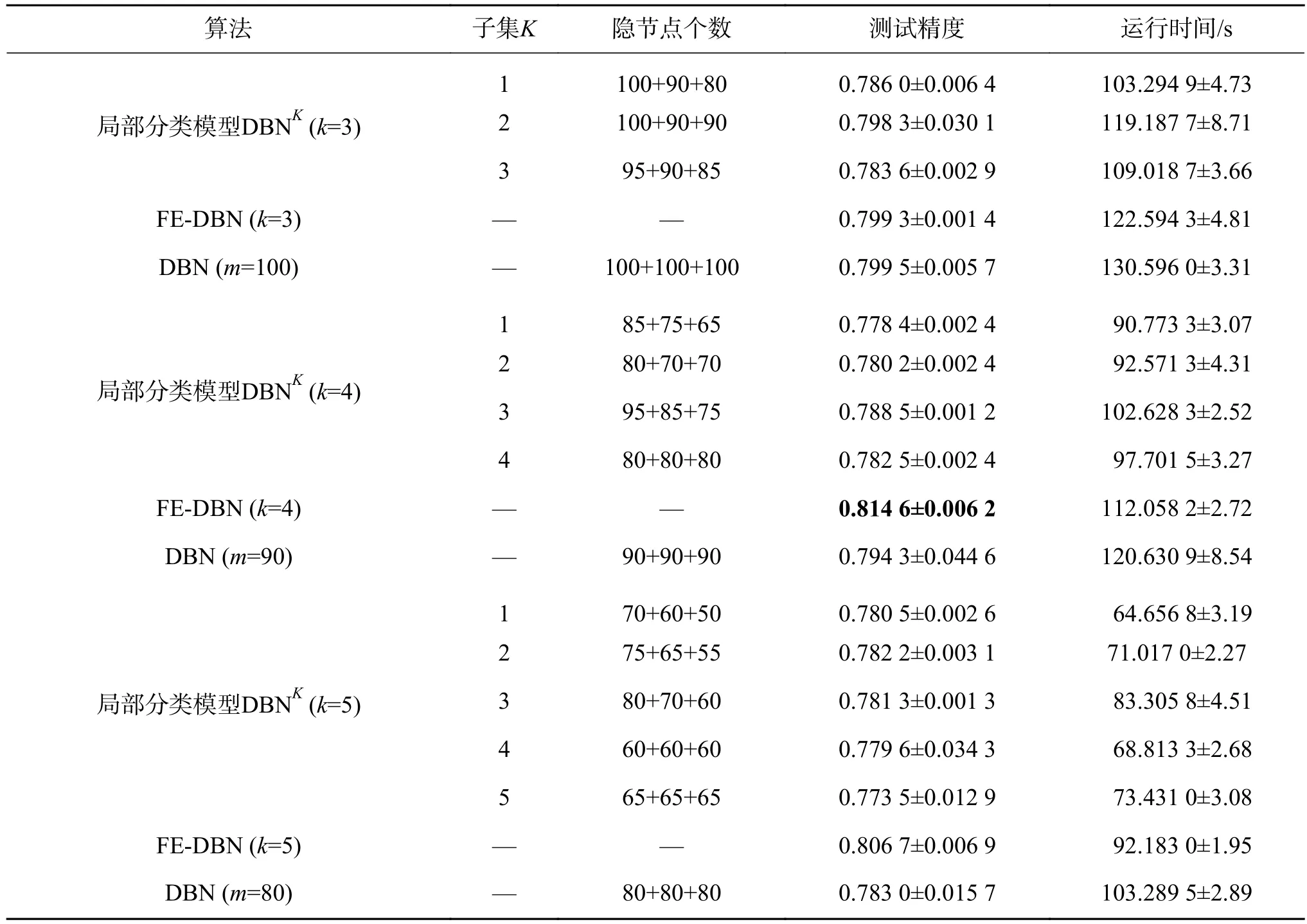
表9 在shuttle數據集上的分類精度及運行時間Table 9 Performance in terms of average testing accuracy and running time with their standard deviation on shuttle

從表5～9的實驗結果，可以得出如下結論：

1)在測試精度上，和全局分類模型DBN相比，FE-DBN在數據集Adult、shuttle和Magic_gamma_telescope上增長較多，在數據集pendigits和waveform3上有略微上浮。在樣本劃分子集確定的情況下，FE-DBN高于任何一個局部分類模型DBNK。總的來看，FE-DBN算法的分類效果在三者中為最優。從表5～9中還可以看出，在劃分的子集數確定時，具有不同隱節點數組合的各局部分類模型DBNK分類器的精度并無明顯差異。隨著劃分子集數的增加，FE-DBN的精度在不同數據集上基本均有增長的趨勢。其主要原因在于，根據集成原理[14,22-23]，對于集成FE-DBN分類模型，增加各子模型的多樣性，能夠提高集成分類器的性能。

2)和全局模型DBN相比較，FE-DBN中每個局部分類模型需要較少的隱節點數，就可以達到較高的精度，這主要是因為組成FE-DBN的每個局部分類器都是弱分類器。

3)對于所有數據集，在運行時間上，當劃分子集數逐漸增多時，由于每個子集的樣本數在減少，隱節點數也在減少，運行時間相應也會減少。由于要進行模糊劃分和模糊集成，FE-DBN的運行時間比各局部分類模型DBNK要多，但是FE-DBN的運行時間要小于全局模型DBN的運行時間，因為在FE-DBN中各局部分類模型是并行運行的，且每個子模型的隱節點數均小于全局模型DBN的隱節點數。

無論是模擬數據集還是UCI數據集，基于模糊劃分和模糊加權的DBN集成分類器(FEDBN)比單分類器(DBN)的性能好，比最優的局部分類模型DBNK也要高。由表3～9中結果，根據統計分析得出，樣本劃分粒度越細，分類精度會越高，表明細劃分能得到更多的樣本特征信息。但也不是子集劃分得越多，精度就越高，數據集shuttle在劃分子集數為4時取得最大值。

4 結束語

采用集成的方法解決DBN訓練時間復雜度高的問題。根據數據之間的相似性信息對數據進行模糊分組，構造樣本空間子集，然后在各樣本空間子集中訓練具有不同結構的DBN子分類器，最后使用模糊加權的方法，得到最終的集成分類器和分類結果。人工數據集和UCI數據集上的實驗結果顯示，FE-DBN算法可以得到比其他分類算法更好的分類結果。未來的研究工作將主要集中在如何確定樣本空間子集上。