基于鄰域系統的智能車輛最優軌跡規劃方法

王星，趙海良，王志剛

（西南交通大學 數學學院 信息與計算科學系，四川 成都 610031）

智能車輛的研究內容十分多樣，例如它的結構設計，控制理論[1-2]，路徑規劃。對于智能車的路徑規劃，設計最優的曲線是此問題的核心。智能車的路徑規劃按照范圍可分為宏觀與微觀2類，按照狀態可分為動態規劃和靜態規劃2類。對于智能車的宏觀路徑規劃，Dijkstra算法、Floyd-Warshall算法，支持向量機算法[3]，A*算法[4-5]等均有文獻進行應用和改進。而對于智能車的動態路徑規劃，人工勢場算法[6]、神經網絡算法、遺傳算法等智能算法也被廣泛的應用。上述算法大多是對宏觀的道路網絡節點進行路徑規劃，然而對于微觀的道路上的軌跡規劃問題，目前國內外文獻較少從最優性這一角度進行考量，還需要進行進一步的探索與研究。對于軌跡規劃問題，基于Dubins路徑[7]的軌跡生成方法是一種可行的方法。此外還有三角函數曲線、圓弧曲線等軌跡生成方法。考慮到曲率連續問題，文獻[7]給出了基于五次多項式的軌跡規劃方法。此外還有文獻采用模糊邏輯控制[8-10]、粒子群算法、蟻群算法等智能算法進行優化與控制。上述文獻給出了十分有價值的理論成果，但大多是對首末位置以及障礙物信息已知情況下的軌跡規劃，不少文獻采用GPS定位方式確定信息，鑒于目前GPS裝置的精度和性能，可能會和實際路況存在較大誤差。因此，在實際道路中目標點的確定依然是一個難題，而鄰域系統理論是一種可行的解決方式。

本文主要以鄰域系統[8-12]理論為基礎，研究智能車在鄰域系統內的最優軌跡，是微觀道路上的軌跡規劃問題。鄰域系統是一個數學上的常用概念，是對事物及其關聯事物體系的抽象描述。本文一方面將數學中的鄰域系統應用于智能車輛具體的控制過程，這里涉及到了設計具體控制規則，實現數學抽象到具體應用的轉變；另一方面將具體的智能車控制過程抽象成一般的數學模型，并通過具體的求解算法，進行數學模型的求解。通過分層決策思想，將動態的車輛運動規劃中近乎無限多的信息縮小至車輛的鄰域系統內，繼而縮小至有限個標準可行鄰域內，從而將復雜道路中的運動簡化為車輛在一系列簡單的鄰域內的靜態決策過程的疊加。因此只需考慮某一個單一鄰域內的最優軌跡規劃問題，這為問題求解帶來了極大地簡化。

對于單一鄰域內的最優軌跡規劃問題。首先根據乘車者的需求對標準可行鄰域內的軌跡曲線尋求泛函極值。具體做法是應用泛函的思想確立軌跡曲線的彎阻指數與長度指數等指標，其中采用曲線曲率的積分定義了曲線的彎阻指數。上述指標的建立是為了模擬乘車者的感受，以彎阻指數為例，若道路曲率越小，則彎阻指數越小，車輛行駛越順暢。按照上述指標的要求，本文建立了最優軌跡曲線的多目標優化模型，并給出了一種實用的和可操作的求解方案，構造了一種采用Hermite插值法的軌跡曲線，并和其他幾類常用的軌跡曲線進行了對比，結果表明本文構造的曲線是一種比較好的滿意軌跡曲線，更接近人工經驗軌跡。

1 智能車輛的鄰域系統

智能車輛會因人們的各類需求而裝配有各類傳感器，例如距離傳感器、紅外線傳感器、超聲波傳感器、圖像傳感器等。當智能車輛在道路上運動時，這些傳感器會給出當前道路包括障礙物的各種信息，用以確定車輛的一個安全行走范圍，這就是車輛的一個可行鄰域，可行鄰域的定義如下。

定義1 可行鄰域[8]

假設狀態論域X的一個有界區域Q(x0, T)滿足：z∈Q(x0, T)，{x(t); x0, T}∈Γ(x0)，使得 z∈{x(t);x0, T}且{x(t); x0, T}Q(x0, T)，則稱 Q(x0, T)是初態x0的一個可行鄰域，其中T稱可行區域的保持時間，Γ(x0)為初始狀態為x0的軌跡集合。

由初始狀態x0的所有可行鄰域構成的集合稱為該狀態的可行鄰域系統，記為FNS(x0)。狀態x0的一個可行鄰域包括了從x0出發的一段時間T內狀態軌跡的集合，在一個確定的可行鄰域內可能含多條軌跡。

要實現智能車等智能輪式機器人的自主移動，首先需要模仿智能生物的行為決策過程。智能生物在面對復雜的動態環境時，通常先尋找一個短時間不變或保持相對穩定的環境作為其下一步活動的決策范圍，然后再進行行為決策。這一決策范圍即可行鄰域，一系列的可行鄰域構成鄰域系統。基于鄰域系統的動態決策模型[8]就是描述這樣一個基于鄰域系統的控制決策過程。其控制過程由以下幾個步驟組成：

1)根據控制過程中觀測變量的特點選擇合適的鄰域系統；

2)通過一些優化方法，在當前狀態下確定一個滿意的可行鄰域；

3)在滿意的鄰域中，根據一些規劃方法給予滿意的決策，實施新的決策行為；

4)在可行鄰域的持續時間內保持相同的行為，直到產生下一個決策；

5)上述過程是一個完整的決策循環。當一個周期完成后，一個新的循環開始依次執行步驟2)～4)。

可以看到，各個鄰域的控制過程不斷重復疊加，從而構成了整個控制過程。模型將復雜的宏觀環境下的動態決策過程分解為一系列簡單的鄰域內的靜態決策過程的組合，簡化了整個決策過程，使得面對的是一個有限的、局部的簡單環境，而不是無限的、復雜的整個世界。由此可見，車輛在道路上的運動軌跡問題被轉化為在每一個可行鄰域里的運動規劃問題的疊加。

如圖1所示，為智能車某一時刻在道路上行駛的示意圖。其中上下兩側的平行線為仿真道路的邊界，道路內部的虛線所圍成的不規則多邊形是傳感器能夠確立的車輛行駛的一個可行鄰域。注意到可行鄰域的形狀與數學表達都很難描述，因此需要建立車輛的標準可行鄰域，其中圖1內虛線圍成的矩形框就是一個標準可行鄰域。鑒于標準可行鄰域沒有一個統一的定義，本文的標準可行鄰域含義如下。

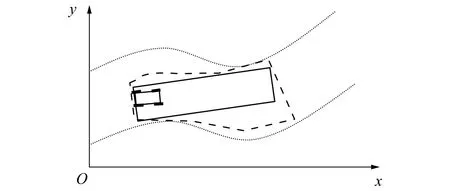
圖1 智能車標準可行鄰域分析圖Fig. 1 Standard feasible neighborhood analysis

標準可行鄰域：可行鄰域中數量有限的特定鄰域。

標準可行鄰域的提出是為了在計算機仿真的過程易于進行模型的建立和數學描述，根據目的的不同可以建立不同形狀、不同大小的標準可行鄰域。如圖2所示，為智能車的標準矩形鄰域。要求標準矩形鄰域的底邊與車體的底邊是重合的。智能車的鄰域系統控制思想可以將復雜的動態控制轉化為簡單的靜態控制。主要包括2個步驟，第一步是將控制范圍縮小至一個局部的可行鄰域，第二步是將局部可行鄰域內的控制簡化至有限個標準的可行鄰域內的控制。

圖2 標準矩形鄰域Fig. 2 Standard rectangular neighborhood

如圖3所示，給出了智能車在3個不同時刻的行駛狀態，其中每一個矩形框為智能車此時確立的標準可行鄰域。智能車在道路上的軌跡規劃就是在一個個局部的標準可行鄰域內的軌跡規劃的累積過程。

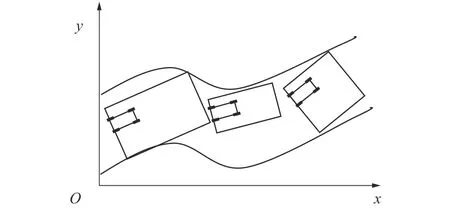
圖3 智能車的動態軌跡規劃Fig. 3 Intelligent vehicles dynamic trajectory planning

2 最優軌跡曲線的評判指標

2.1 基于鄰域系統的最優軌跡曲線

在本文的智能車控制系統中，設Q為標準可行鄰域系統，則尋求最優軌跡曲線可以抽象為對標準可行鄰域內的信息尋求泛函極值的過程。

對最優軌跡曲線的選取進一步細分，可根據不同的需求劃分如下：

1)用時較短；

2)行走路徑較短；

3)乘客感到舒適。

這是一個多目標優化問題，上述問題的最優解是車輛在標準可行鄰域內的最優曲線。

2.2 最優軌跡曲線的評判指標

由上述需求，對于軌跡曲線L的軌跡方程y=y(x)。構造規則如下：

1)軌跡曲線的首尾位置是固定的，起始位置為當前鄰域相對坐標系的原點，末位置為當前標準可行鄰域的尾部中點向左平移一個車體長度。

2)軌跡曲線的方程為單值函數，即對于自變量x，其對應的函數值f(x)是唯一的。

3)軌跡曲線是連續的。

如圖4所示，曲線A不滿足構造規則2)，不是本文的軌跡曲線。這也是符合實際駕駛經驗的，車輛在單行道路行駛時，不會出現反向行駛的情況。曲線B，C為車輛的軌跡曲線。

對于軌跡曲線，如何在軌跡曲線族中選取最優的軌跡曲線是整個軌跡規劃理論的關鍵。考慮多目標優化條件，本文給出下述2個指標。

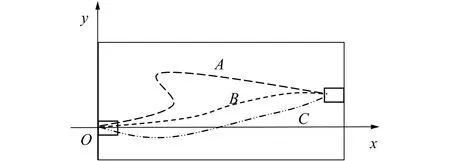
圖4 曲線構造圖Fig. 4 Curve construction diagram

定義2 長度指數

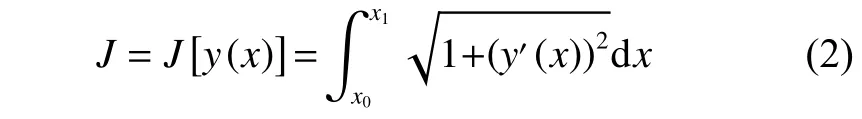
稱之為曲線L的長度指數。

定義3 彎阻指數

稱之為曲線L的彎阻指數。

長度指數是衡量首末位置等同的不同軌跡的駕駛長度。一般來說，對于一固定首末點的曲線，軌跡長度越短，可以認為沿此曲線行駛的駕駛效率越好。

車輛行駛的彎阻指數主要取決于行駛軌跡的順暢，不同于軌跡曲率這一局部概念，是一個整體性的概念。對于行駛軌跡的平穩，易知曲率越小，軌跡越順暢，乘客越舒適。其次由定義式可知，彎阻指數取決于軌跡的固有特征，與其他因素無關，是描述軌跡性質的常數。

對于定義3，可給出推論1：

推論1 對于A、B兩條首末位置相同的曲線，若A曲線每一點的曲率的絕對值都小于B曲線，則A曲線的彎阻指數小于B曲線。

由推論1顯然可以得出，對于2條定長曲線，曲率越小的曲線越令人感到順暢。

2.3 評判指標的標準化

為了便于進行指標的評判和比較，本文的指標標準化方法如下：

定義4 距離優度

稱之為曲線L的距離優度。

對式(4)進行化簡，令

定義5 順暢度

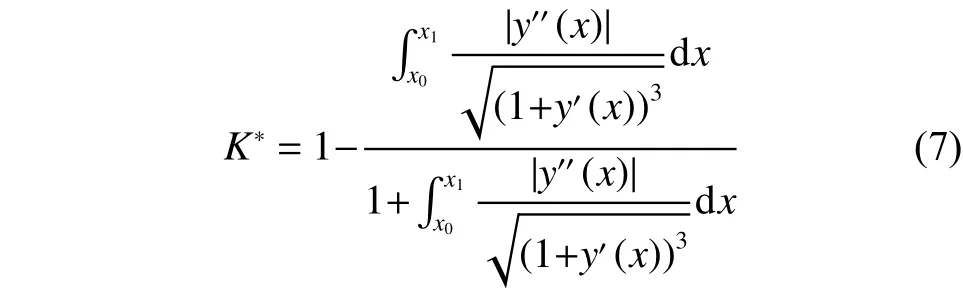
稱之為曲線L的順暢度。

結合定義3對式(7)進行化簡，則有

曲線L的順暢度是彎阻指數的標準化過程，考慮到直線的曲率為0，因此標準化的過程就是將彎阻指數的范圍從映射到[0,1]區間上。當彎阻指數K為0時，代入式(8)，取1；當彎阻指數為時，取0。因此的取值越接近1越令人感到順暢。

在實際應用時，可根據不同需求選用指數型指標或標準化指標。對于不同駕駛風格的駕駛員，可初步劃分為駕駛平穩型和追求速度型，他們對于上述2個指標是有著不同偏好的。為了綜合評判不同駕駛員對于最優軌跡曲線的要求，現引入對于最優軌跡曲線的綜合評判指標。

定義6 綜合評判指標

稱之為曲線L的綜合評判指標，其中w1、w2為不同駕駛風格的駕駛員對于J*、K*指標的權重，可由專家評判給出。

綜上可知，在眾多軌跡曲線中選取一個最優曲線，只需比較不同軌跡曲線的綜合評判指標的值，數值最大的曲線即為所求。

3 最優軌跡曲線模型及其求解方法

3.1 最優軌跡曲線模型及其滿意條件

首先建立最優軌跡曲線的多目標優化模型—最優軌跡曲線模型 對于標準可行領域Q內的軌跡集合Γ(x0)，尋求最優軌跡曲線,使得下列目標函數可取得極值

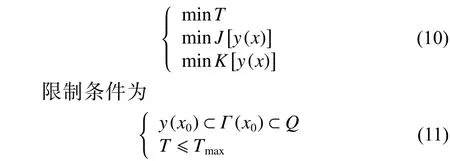
式中：T為智能車在標準可行鄰域內完成規劃的軌跡所用的總時間；完成規劃的軌跡能夠接受的最長時間；J、K分別為軌跡曲線的長度指數和彎阻指數。目標函數的最優解為最優軌跡曲線，此模型可簡寫為OTC模型。

盡管式(10)給出了最優軌跡曲線模型，但該模型的一般求解是困難的。在實際問題中只需給出一種實用的、可操作的構造方法即可。因此需要給出滿意曲線的滿意條件。尋求滿意曲線的過程是一個篩選與嘗試的過程，需要建立合理的限定規則，提高篩選與嘗試的效率。參考圖4的3條曲線，其中曲線B是一條符合生活經驗的滿意曲線，考慮到曲線B的特征，本文的規則如下：

規則1：車體軌跡應較為光滑。

規則2：車體的末位置應盡可能滿足底邊中點到鄰域兩邊是等距的要求，即在鄰域中部運動。

基于上述規則，滿意條件如下：

定義7 p-水平滿意集

為曲線y(x)的p-水平滿意集。

由式(12)可知，根據目標閾值p，可求出滿意曲線的集合B，若最優曲線的集合為C，易知，因此可通過逐步迭代法來尋找滿意曲線。

3.2 滿意曲線的求解算法

如圖5所示，為智能車的鄰域坐標系，其中車體與可行鄰域底部的中點距離為s，鄰域長為H，車體長為l。假設軌跡曲線二階光滑，其中初始位置坐標為 o(0，0)，末位置坐標為 (H-l，s)，且二者一階導數皆為0；Hermite插值法可以將函數值和導數值完全利用， 根據插值節點的個數不同，可求出不同的軌跡曲線，兼顧滿意度和復雜性，本文將插值節點的個數定為3個。則滿意軌跡曲線的迭代算法如下：

1)確定初始值。

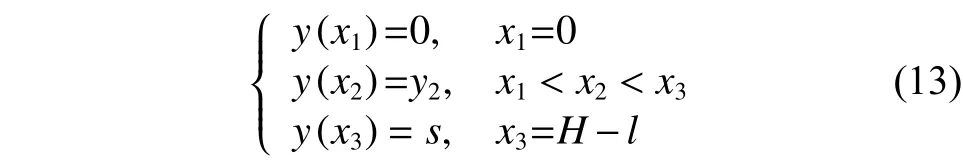
導數值滿足

式中O1(x1, y1)、O3(x3, y3)為已知節點，因此需要確定節點O2的坐標值和導數值。假設滿意軌跡曲線對稱，則節點O2的坐標值為曲線中點，導數值k是一個和鄰域大小相關的量，可設初始值為

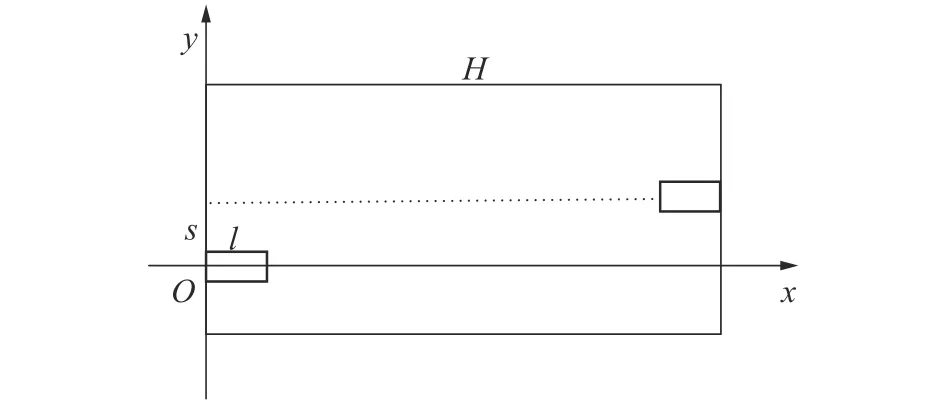
圖5 智能車的鄰域坐標系Fig. 5 Neighborhood of intelligent vehicles coordinate system

2)計算軌跡曲線指標。

將上述數據代入，函數f(x)在節點處的插值多項式為

根據多項式計算長度指數和逆舒指數，并選擇合適的權重，計算式(9)的綜合評判指標，執行3)。

3)計算導數值。

對于導數初值 k0，確定搜索區間 [αk0,βk0],其中 α＜1, β＞1，設步長為 t，對于每次迭代 i，導數值為

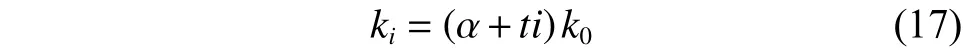
按照上述算法，本文以滿意度指數p=0.8，權重w1=0.4、w2=0.6，所計算出的節點O2的坐標值和一階導數如下：

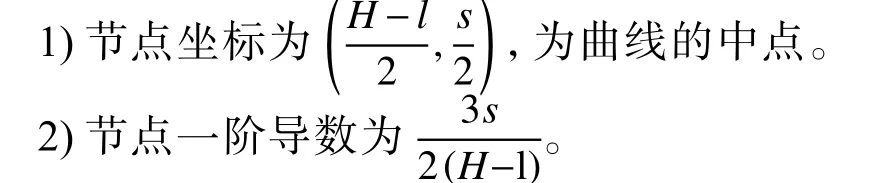
3.3 滿意曲線的理論分析

對于上述操作算法，首先證明最優軌跡曲線的存在性。

由算法的構造過程可知，曲線首末位置已知，斜率均為零；插值點為曲線中點，斜率可連續變動。因此對于斜率搜索區間[αk0,βk0]，由閉區間有界。又由連續函數的四則運算以及最值定理可知，存在最優值

這就證明了最優軌跡曲線的存在性。其次由滿意曲線的求解過程可知，每次迭代產生的子列，有

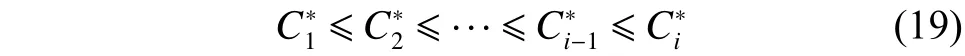
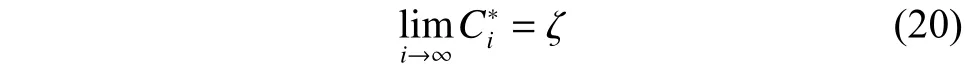
因此本文給出的求解算法是可行的。

4 仿真結果以及同其他文獻的對比

目前利用鄰域系統的思想進行智能車研究的國內外文獻較少，因此同其他文獻研究成果的對比主要在于敘述各文獻的研究思路和解決問題的思想與本文的異同點。

本文的研究區別于一些文獻所研究的靜態規劃[3]問題, 適用于智能車在道路上的動態規劃。

對于此動態規劃問題目前可分為3個不同層次。第1個層次是對于宏觀的道路網絡節點進行路徑規劃，文獻[4]主要研究這一問題，是對整個交通信息網的統籌規劃。

第2個層次是在宏觀路徑規劃的基礎上，對于微觀的行駛軌跡進行研究。這個層次又可細化成2種研究方式，一種是行駛軌跡直接默認；例如文獻[5]采用激光雷達進行定位，對于障礙物的規避軌跡直接默認了Dubins路徑。另一種研究方式是根據實時信息進行軌跡自主規劃；例如文獻[6]運用人工勢場算法對路徑進行搜索；例如文獻[7]給出了一種基于三角函數的軌跡搜索方法。

第3個層次是根據目前規劃出的運動軌跡，控制智能車進行軌跡的跟蹤。

本文研究上述分類中的第2個層次，并且研究方式是對于已知的道路信息以及障礙物，根據智能車的傳感器對周邊的道路信息進行實時的采樣分析，從而進行軌跡的規劃與搜索。本文采用了鄰域系統的相關理論，目前對于在鄰域系統的路徑規劃的文獻[8]-[12]大多還需要進一步的改進，其中文獻[8]雖奠定了鄰域系統控制的基礎理論，但僅用于智能車實施可行鄰域的選取，對鄰域內的路徑規劃未做深入研究。文獻[9]給出了倒車環境下的軌跡規劃，對于復雜道路上的軌跡規劃還需要進一步研究；文獻[10-11]利用鄰域系統理論，給出了很多初步的研究結果。其中文獻[11]給出的滿意解的論述是一種可行的研究方法，本文滿意曲線的建立沿用了此思想；文獻[12]建立了障礙物的避障規則和鄰域內的移動規則，但未考慮軌跡的順暢和效率問題。綜上所述，上述文獻做出了很多有建設性和啟發性的工作，但是首先從運動軌跡入手，以構造軌跡的平穩光滑為首要目標，來解決軌跡規劃問題，目前還是鄰域系統的一個欠缺部分，本文主要完善了這一問題。

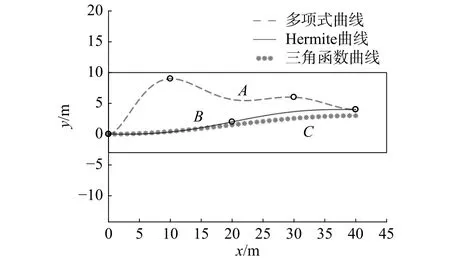
圖6 實例對比圖Fig. 6 Example comparison chart

如圖6所示，為智能車在某一時刻的鄰域相對坐標系。為便于進行數據的比較，對其中一些數據進行了放縮。其中標準可行鄰域長為45 m，寬為14 m；智能車長為5 m，距離鄰域底部中心3 m。A、B、C為3條軌跡曲線，其中A曲線為多項式曲線, 由圖形“--”表示；B曲線為本文所構造的5次Hermite插值曲線，與C曲線十分接近，在圖7表示為一條連續的曲線；C曲線為文獻[7]提到的三角函數曲線，由圖形“*”表示。3條軌跡曲線的方程如下：

現分別求出軌跡曲線彎阻指數K，則有

最后進行綜合評判。以駕駛穩定型駕駛員為例，設駕駛員對于J*、K*指標所取權重為w1=0.3、w2=0.7，代入計算可得

如圖7所示，為本文的軌跡曲線在道路上的仿真圖。本文從鄰域系統入手，重點搜索標準可行鄰域內的滿意路徑。在現有的鄰域系統相關文獻中，很少有文獻從控制軌跡的平穩光滑角度去搜尋滿意控制規則，忽略了控制軌跡的順暢度和效率。下圖為文獻[10]-[11]的控制仿真圖，同本文仿真圖對比可以看出，本文的控制理論在軌跡的平穩光滑性上具有一定的優越性。

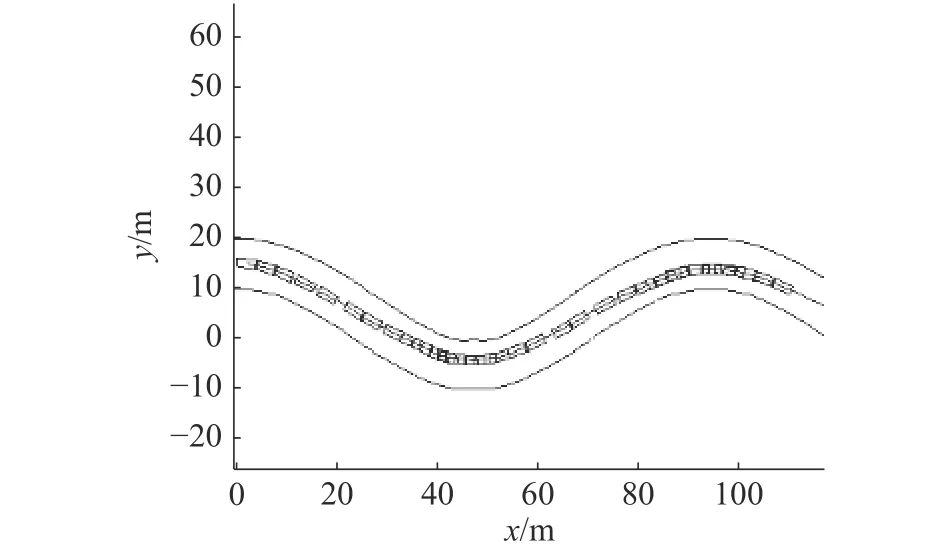
圖7 道路仿真圖Fig. 7 Road simulation

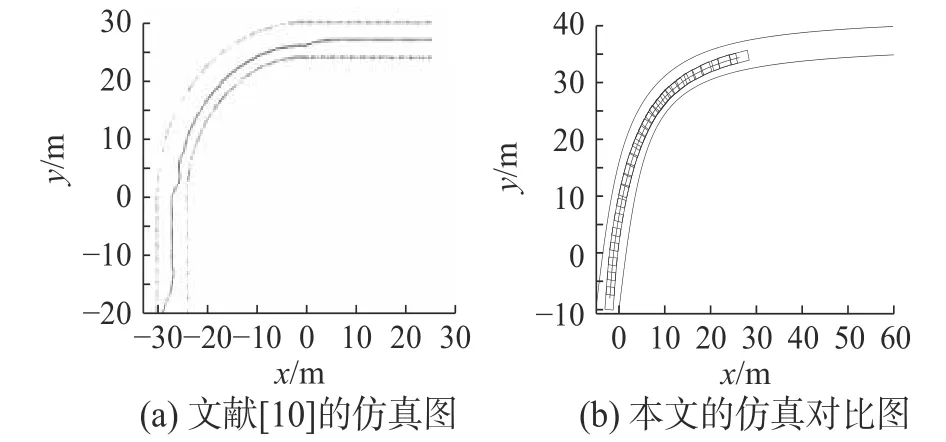
圖8 文獻[10]與本文仿真圖對比Fig. 8 Comparison of the literature [10] with the simulation of this paper

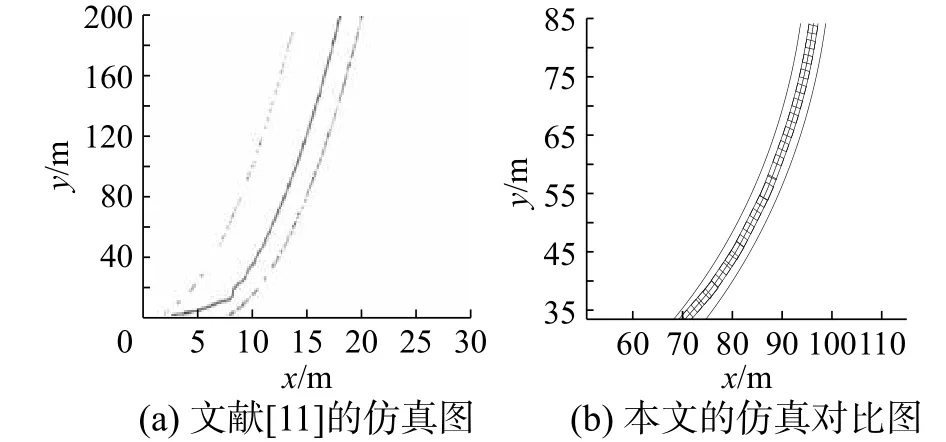
圖9 文獻[11]與本文仿真圖對比Fig. 9 Comparison of the literature [11] with the simulation of this paper

5 結束語

對于微觀的道路上的最優軌跡的規劃問題，鄰域系統理論可以將復雜動態過程轉化為簡單靜態過程，簡化了問題的復雜性。本文定義了曲線的彎阻指數和長度指數，并以此為基礎給出了鄰域內最優軌跡的綜合評判求解模型，給出了一種滿意的軌跡曲線算法。仿真結果說明了本文的規劃理論在軌跡的平穩光滑性上具有一定的優越性。