基于模態追蹤的地鐵車輛低頻橫向晃動分析

陳迪來,沈 鋼,宗聰聰

(同濟大學 鐵道與城市軌道交通研究院， 上海 201804)

當前，某型高速列車和部分地鐵車輛容易出現車體橫向晃動，而這種橫向低頻晃動可能惡化車體橫向平穩性指標，影響旅客乘坐的舒適性[1-2]。產生軌道車輛車體低頻晃動的原因很多，但最根本的還是車體與轉向架之間的耦合振動[3]。轉向架蛇行運動頻率往往跟車輛的運行速度直接相關，其頻率隨著列車運動速度的提高而增大。然而，車體的下心滾擺、上心滾擺、搖頭等橫向運動的自振頻率不隨車輛運行速度的變化而變化，且自振頻率較低，可能導致轉向架與車體發生共振[4]。

目前，大多數學者對轉向架蛇行進行了詳細研究，但是對于車體橫向低頻晃動研究較少。Huang等[5]建立反映車體和轉向架相互耦合關系的車輛系統多剛體動力學模型，分析車體蛇行的關鍵影響參數，借用線性分析方法，分析敏感參數對高速車輛橫向異常晃動的規律。Iwnicki[6]指出當等效錐度較低時，容易出現車體不穩定的蛇行運動；當等效錐度較大時，容易出現轉向架蛇行振動。J?nsson等[7]指出車體蛇行運動在運行速度較低時，由車體固有的幾種模態共振引起，如車體的搖頭、對稱低頻擺動、非對稱低頻擺動。劉繼領[8]采用多體系統動力學仿真計算方法，研究CRH1E型動車組車體嚴重晃動的原因，并提出相對應的衰減橫向晃動的解決方案。李然等[9]利用多體動力學軟件仿真分析在不同摩擦系數、等效錐度等工況下，車體橫向振動的加速度以及橫向平穩性，發現當等效錐度和摩擦系數均處于較小值時，容易出現車體的橫向晃動。王開云等[10]仿真分析了某型機車在實際線路上出現的橫向異常振動現象，為消除機車的異常晃動現象，提出兩種參數優化方案，經試驗驗證，優化后機車的橫向晃動消失。葉一鳴等[11]針對機車異常晃動現象進行了研究，發現軌道狀態的不良容易引起車體異常振動，并針對這個現象提出了一些預防措施。

車輛剛體模態能清楚表達出車輛系統各自由度振動的頻率和振動的衰減程度，但從車輛剛體模態的角度對車體橫向低頻晃動的研究還很少。本文基于歐式貼近度對鐵道車輛剛體模態進行模態追蹤，得到剛體模態的頻率和阻尼比隨著運行速度變化的規律，分析了某地鐵車輛車體橫向低頻晃動的原因。在歐式貼近度的基礎上，提出模態間的耦合度這個概念，以減少耦合度和消除橫向低頻晃動為設計目標，對車輛系統的懸掛參數進行了優化。

1 模態追蹤

1.1 歐式貼近度

為了在某模糊集合中，找出同一類型的子集，需對整個集合中的每個子集進行相似性分析，相似性越大，則屬于同一類集合，差異性越大，則不屬于同一類。常見的相似性分析方法是歐式距離，歐式距離越小，說明相似度越高；反之，歐式距離越大，說明差異性越大。E和F為兩個模糊集合，則歐式距離為[12-13]

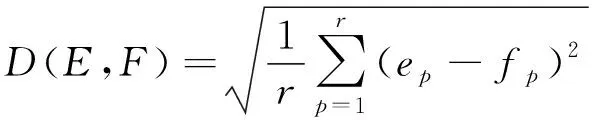
(1)

式中：r為集合的基數；E={e1,e2,…,er}，ep∈E，ep≥0；F={f1,f2,…,fr}，fp∈F，fp≥0。

為了更好度量歐式距離，將計算數據進行預處理(歸一化處理)，即

(2)

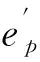
為更好度量兩集合的貼近程度，計算兩集合間的歐式貼近度

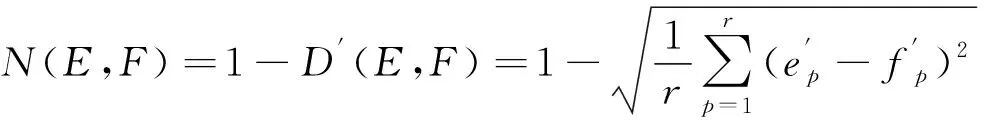
(3)

式中:N(E,F)為歐式貼近度。從式(3)中可以看出，N(E,F)越大，集合E、F越接近，N(E,F)越小，說明集合E、F差異性越大。

1.2 車輛系統的特征值及特征向量

某地鐵車輛自由振動的線性化方程為[14]

(4)

式中：M、C、K分別為車輛系統的質量矩陣、阻尼矩陣、剛度矩陣；Cwr、Kwr均為與輪軌接觸參數有關的矩陣；q為n階(n個自由度)廣義位移向量；v為車輛運行的速度。

假設

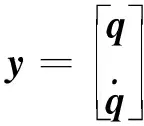
(5)

將式(5)代入式(4)，可將其轉化為

(6)

式中：A為這個車輛系統的特征矩陣。

對特征矩陣A進行QR分解，得到系統的特征值λ和特征向量γ

q=γeλt

(7)

將式(5)、式(7)代入到式(6)中，可以得到

(A-λI)γ=0

(8)

式(8)有非零解的條件是

|A-λI|=0

(9)

由式(9)所得到的解λ就是系統矩陣A的特征值，分別為λ1,λ2,λ3,…,λ2n，特征值λ的普通形式是一對共軛復數，當特征值共軛時，取一個即可。則特征值λj(j=1,2,…,n)對應的特征向量γ也有2n個，分別為：γ1,γ2,…,γ2n，特征向量也是復特征矢量，取一個即可。計算得到車輛系統的特征值和特征向量之后，去掉特征值虛部為0的數據，得到m個n維共軛復數特征向量Xi，記為

(10)

對特征向量的幅值進行數據預處理，設

(11)

(12)

式中：xik為復數；|xik|為復數xik的模；Xi為復數矩陣；|Xi|為復數矩陣Xi的模。

不考慮相位角的超前或滯后，對特征向量Xi的相位角進行數據預處理

φik=θik-max(θik)

(13)

即系統所有模態相位角ψi=[|φi1| |φi2| … |φin|]T。

式中:θik為相位角；φin為復數，|φin|為復數φin的模。

表1為速度為V1工況下車輛各模態的特征向量。

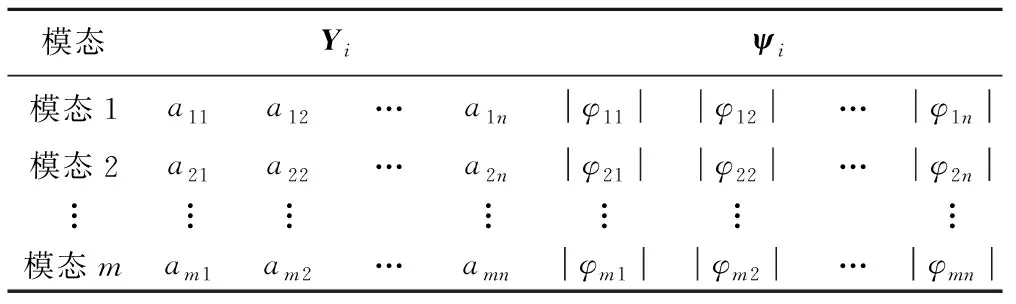
表1 速度為V1時特征向量

1.3 車輛系統的模態追蹤

根據歐式貼近度，計算不同速度下各剛體模態的相似程度[15]

j=1,2,…,mi≠j

(14)

式中：NYij為兩個模態振幅的歐式貼近度；aik為第i個模態的第k個自由度的幅值；ajk為第j個模態的第k個自由度的幅值；α為振幅的權重。

(15)

式中：Nψ ij為兩個模態相位角的歐式貼近度；φik為第i個模態的第k個自由度的相位角；φjk為第j個模態的第k個自由度的相位角；β為相位角的權重。

Nij=ω×NYij+(1-ω)Nψ iji≠j

(16)

式中：Nij為兩個模態綜合歐式貼近度；ω為振幅在綜合歐式貼近度中所占的比例。

第j列中的第i個數值Nij最大，就說明：參數V1的第i個模態與參數V2的第j個模態最相似。根據歐式貼近度概念，參數V1的第i個模態與參數V2的第j個模態屬于同一類模態。

2 車體橫向晃動分析

2.1 車輛系統模型

為了研究車體橫向低頻晃動情況，建立整車多剛體線性化模型，見表2，模型共23個自由度。車輛參數見表3，假定輪對與鋼軌不分離、懸掛元件的特性參數均線性，將蠕滑系數視為常數[3]，將車輛系統的輪軌接觸幾何關系線性化處理。

表2 模型的自由度

2.2 車體橫向低頻晃車原因分析

利用MATLAB軟件根據歐式貼近度對23自由度車輛的剛體模態進行了追蹤，仿真速度從2 km/h依次遞增至120 km/h，速度步長不宜過大，否則將導致識別不準確。轉向架蛇行運動、車體上心滾擺和車體搖頭這三種模態對車輛橫向振動影響較大，因此主要針對這三種模態進行分析[4]。

對等效錐度為0.1、0.2、0.3三種工況分別進行仿真分析，結果見圖1。轉向架蛇行運動頻率與車輛運行速度有關，且呈線性增大，但是車體上心滾擺頻率和搖頭頻率基本不隨速度的變化而變化。可見利用模糊數學的模態追蹤方法能實現對剛體模態的自動識別和歸類。在某一個速度段內，轉向架蛇行運動的頻率(同相或者反相)可能和車體固有的上心滾擺或搖頭振動頻率相接近，此時，這兩個模態的歐式貼近度接近于1，即轉向架蛇行運動與車體橫向運動的振動形式極為相似，導致兩種振動發生共振，引起車體的橫向振動加劇。此時，車體上心滾擺的阻尼較小，車體橫向出現低頻晃動現象。從圖1中還可以看出，車體固有的上心滾擺的阻尼比隨著速度增大先增大后急劇下降，并且在與轉向架蛇行運動頻率(同相)相接近的速度區間時，阻尼比的數值下降到最小。阻尼比的劇烈下降，可能引起相應振型的不穩定，導致不穩定振動出現。如果轉向架蛇行運動(同相)與車體上心滾擺、轉向架蛇行運動(反相)與車體搖頭運動分別發生共振的速度區間大致相同時，將進一步加劇車體在這個速度區間的橫向晃動。從圖1(a)、圖1(b)中可以看出：轉向架蛇行運動與車體上心滾擺和搖頭發生耦合的速度區間為50～60 km/h，在此區間內，車體上心滾擺的阻尼比最低下降到13%左右，阻尼比越小，耗能越慢，說明此時車體的上心滾擺振型有可能導致不穩定振動。對比三種等效錐度下的頻率和阻尼比曲線可以看出，雖然在不同的等效錐度下，發生共振的速度區間不同，但是發生共振的頻率基本相同，約為0.85 Hz；隨著等效錐度的增大，車體上心滾擺的阻尼比也逐漸增大，說明了等效錐度越小，車體越容易發生低頻晃動。

由于鐵道車輛存在特殊的輪軌關系，在不同運行速度下，車體的某些模態的振動特征可能發生變化。等效錐度為0.1，在不同運行速度下，車體上心滾擺和轉向架蛇行(同相)運動模態的車輛系統23自由度振動的幅值見圖2、圖3。車體上心滾擺模態各自由度的振幅基本不隨速度的變化而變化；但轉向架蛇行(同相)模態各自由度的幅值在不同速度下差異較大。在運行速度為50 km/h時，車體上心滾擺模態各自由度的幅值與轉向架蛇行(同相)模態各自由度的幅值相接近，說明此時兩振型非常相似。結合圖1分析得，在此速度下，車體上心滾擺的頻率與轉向架蛇行運動(同相)的頻率相接近時，兩個模態的振型非常相似，導致這兩種振動發生耦合共振。此時，車體上心滾擺的阻尼比又較小，車體橫向出現異常的低頻振動。

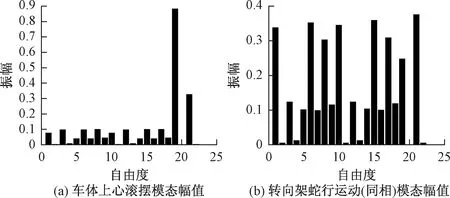
圖3 仿真速度為70 km/h的模態振幅

3 耦合度分析

3.1 耦合度定義

耦合是指多個振動相互影響，并且彼此相互作用的一種現象。車輛系統的耦合度是指車輛系統中多個振型間的耦合程度[16]

(17)

耦合度D越接近100，說明整個車輛系統各模態間耦合程度越大，發生共振的可能性也越大。

3.2 耦合度計算

從圖4中可以看出，當等效錐度為0.1、速度為50～60 km/h時，耦合度的數值很大，這與圖1中頻率圖得到的共振速度區間相同；其余等效錐度下，計算得到耦合度較大的速度區間與圖1中共振的速度區間也相同。這說明利用耦合度能很好地描述共振區間，并且等效錐度越小，耦合度的數值越大，這與等效錐度越小時，越容易發生車體的低頻晃動相吻合[3]。

圖4 幾種不同等效錐度下的耦合度

4 參數優化

本文根據耦合度的概念，以降低系統各模態之間的耦合度為優化目標，對車輛系統的懸掛參數進行了優化設計。

將初始車輛的抗側滾扭桿由原來的1.5 MN/rad，減少到0.5 MN/rad，將二系垂向減振器阻尼由原來的40 kN/(m/s)增大到70 kN/(m/s)，將二系橫向減振器阻尼由原來的58 kN/(m/s)增大到90 kN/(m/s)，其余參數不變。假設車輪的等效錐度為0.1，仿真速度為2～120 km/h，優化后仿真結果見圖5。

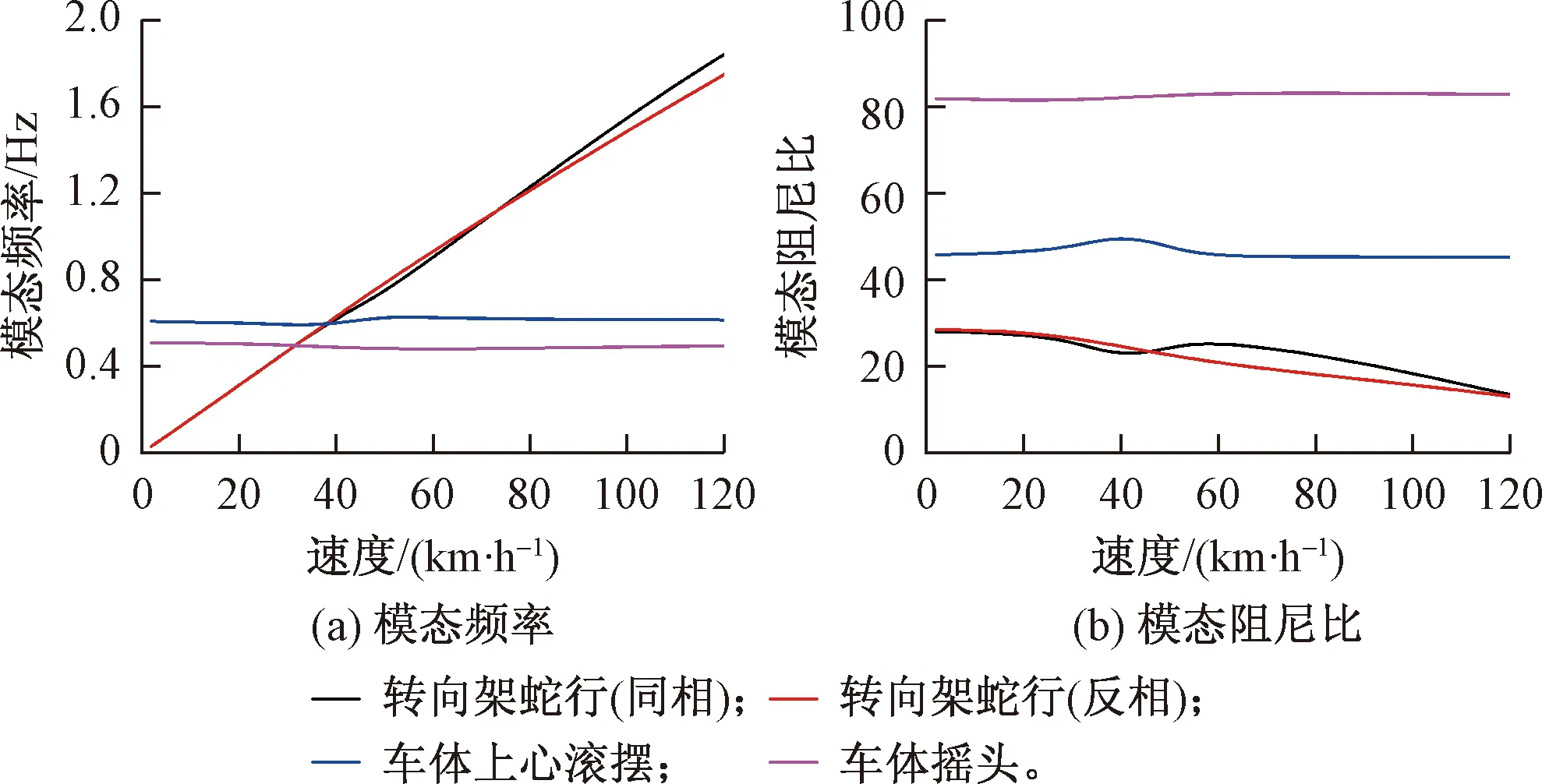
圖5 優化后的模態隨速度變化曲線

從圖1(a)和圖5中可以看出，雖然在速度35 km/h左右時，轉向架蛇行運動的頻率與車體的上心滾擺和搖頭頻率相接近，但沒有發生耦合現象，此時轉向架蛇行(同相)運動模態和車體上心滾擺模態的歐式貼近度約為0.8。并且車體的上心滾擺的阻尼比并沒有出現明顯下降的過程，車體上心滾擺的阻尼比也由原來的25%上升到45%，車體搖頭運動的阻尼比由原來的45%提升到80%，同時有效提高了車體橫向振動的穩定性。因此，為消除車體橫向晃動現象，可以增大車體橫向振型的阻尼比。

優化前后的耦合度-速度曲線見圖6，優化前后系統的最大耦合度分別為88.4、71.7，優化后系統的最大耦合度下降了18.9%。有效降低了系統耦合振動的可能。

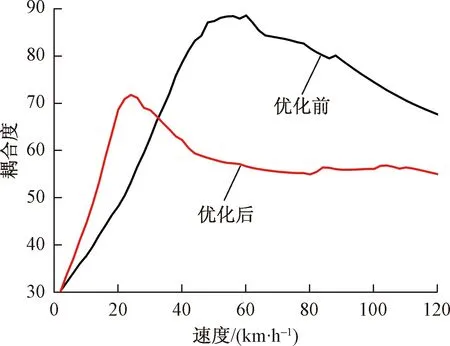
圖6 優化前后的耦合度

5 結論

(1) 基于歐式貼近度準則，能快速、準確計算出車輛系統在不同速度條件下各剛體模態的相似度，得到不同速度下各剛體模態的頻率和阻尼比的變化規律。

(2) 在某速度區間，轉向架蛇行運動(同相)的頻率與車體固有的上心滾擺頻率相接近時，此時兩個模態的貼近度接近于1，說明這兩個振型的振動形式極為相似。并且在此區間內，上心滾擺的阻尼比下降，阻尼比越小，系統的耗能越慢，易導致系統發生不穩定的振動。此時轉向架蛇行(同相)引起的車體上心滾擺與車體固有的上心滾擺振動將發生共振。同理，轉向架蛇行運動(反相)與車體搖頭運動發生共振，可能導致車體橫向晃動。

(3) 通過優化設計車輛的懸掛參數，使轉向架蛇行運動與車體固有振型發生耦合的程度降低，增大車體橫向振型的阻尼比，使車體橫向振動的穩定性增強，從而消除車體的橫向異常晃動現象。

(4) 利用耦合度為分析車體橫向低頻晃動問題提供可優化的目標函數，耦合度數值越大，說明車體系統發生耦合振動現象越嚴重，發生共振的可能越大。