一種結合時刻表調整的列車節能駕駛優化方法
盛 昭,蔡伯根,上官偉,2,王 劍 ,2
(1.北京交通大學 電子信息工程學院,北京 100044;2.北京交通大學 軌道交通控制與安全國家重點實驗室,北京 100044)
近年來,我國高速鐵路行業發展迅速。截至2016年底,國內高速鐵路營運里程已經達到2.2萬km,2017年6月25日“復興號”中國標準動車組在京滬高鐵正式雙向首發[1],并于9月21日率先實現了時速350 km運營,成為了世界上運營時速最快的高速列車。高速鐵路在給廣大群眾帶來快捷便利的同時,大量的能源消耗也成為一個不能忽視的問題。在保障高速列車系統安全可靠的前提下,開展以降低高速列車運營能耗水平為目的的關鍵理論技術與方法研究具有重要現實意義。有關列車運行節能優化方面的研究可以從以下幾個方面考慮:
(1) 車體本身的優化研究:采用輕量化車體的設計以及流線形車頭的設計來減少運行中的阻力,使用高效率牽引設備提高能量的利用率。
(2) 軌道線路優化設計的研究:通過減少線路中的坡度、曲線段以及隧道來減少運行中的阻力。
(3) 列車駕駛策略的優化研究:通過速度曲線優化、再生制動的使用減少運行中的能耗。
(4) 列車運輸組織的優化研究:通過優化運行圖和時刻表降低線路整體運輸能耗。
前兩方面是線路、車輛設計之初需要重點考慮的問題,本文的研究工作重點關注后兩條。文獻[2-3]對列車節能駕駛和時刻表優化兩個方面的研究工作進行了詳細的總結。
在列車操縱優化方面,文獻[4]將動態規劃法和離散型數學解析法應用于求解水平軌道無限速的列車運行模型。文獻[5]提出了基于簡單模型的列車運行優化方法,并給出了幾種列車運行最優軌跡的描述。文獻[6-7]應用極大值原理進行了基于線性能耗優化的列車運行最優工況序列推導,得出了列車節能運行工況序列為最大加速,惰行和最大制動;在長距離運行區間內,列車節能運行工況序列還應包括巡航工況[8]。文獻[9]采用惰行控制方法研究了路網環境下的列車節能運行問題。文獻[10]采用差分進化算法研究了列車運行操縱的多目標優化問題。文獻[11]基于遺傳算法研究了以節能為目的的列車控制模型和列車運行調整方法。文獻[12-13]與其研究團隊在列車運行優化問題上做了大量分析研究,分析了在有限速和無限速兩種情況下的最優運行策略。文獻[14]研究了多輛列車運行于沖突區段時的運行優化問題,采用黃金分割搜索法求解列車在沖突區段能耗最低的運行速度。文獻[15]在列車運行優化的研究中,考慮了鐵路系統結構的復雜性和不同列車的載重差異性,提出一種基于能耗與時間的列車調度模型,并利用Pareto優化理論求解該模型的最優解。
在列車運輸組織優化方面,文獻[16]針對高速鐵路列車運行圖的優化和評估問題,提出以控制列車晚點傳播為主要目的的可恢復魯棒性優化模型。文獻[17]以列車旅行時間和動車組接續時間最小化為目標函數,建立了高速鐵路列車運行圖綜合優化模型,并給出求解方案。文獻[18]以最大社會效益為目標建立了公交化城際列車時刻表優化模型。文獻[19]通過考慮再生制動最大重疊時間來優化城軌列車的時刻表。文獻[20]綜合考慮了列車控制優化和時刻表優化的問題,建立了移動閉塞下的多相位最優控制問題,采用Matlab的GPOPS工具箱進行求解。文獻[21] 提出了綜合描述高速列車時刻表優化和運行曲線優化的“空間-時間-速度”網絡框架,并采用動態規劃方法進行求解。
綜合國內外的相關研究可以發現,目前關于列車運行優化方面已經有大量研究成果,且有部分研究成果已經應用于工程實踐。但是大部分研究工作將列車節能駕駛問題和時刻表優化問題單獨考慮,綜合考慮兩者的研究相對匱乏。
基于上述分析,結合我國高速鐵路運營的基本特點,本文在以往研究的基礎上,研究基于時刻表調整的列車駕駛節能優化方法。首先,建立高速列車多站間運行的離散狀態空間模型;然后,以巡航速度、制動初速度為決策變量,以區間運行能耗、運行時間為目標建立高速列車多站間節能運行優化模型,利用基于模擬退火的粒子群算法求解以“能耗-時間”為雙目標的Pareto最優解集,并通過最小二乘法擬合得到每個區間相應的Pareto曲線;在此基礎上,利用“能耗-時間”Pareto曲線,建立多站間時刻表調整優化模型,基于KKT條件對連續站間的時刻表優化調整問題進行求解,得到最優的站間運行時分組合和最佳區間運行策略。
1 高速列車多站間運行優化問題
1.1 高速列車區間運行基本過程
對于已建成的軌道線路,線路信息是固定的,同時固定型號的列車牽引和制動特性參數也是確定的。因此,高速列車在站間的速度曲線優化是研究列車節能運行的基礎。高速列車運行過程中,在列車運行控制系統的監督下根據同一區間前行列車的位置、速度以及線路信息的變化,更新行車許可,根據更新的行車許可終點生成“速度-距離”模式曲線,監控列車的安全運行。列車在站間存在多種可行的速度曲線,根據文獻[8],列車在一個區間內的最優駕駛策略為“最大牽引-巡航-惰行-最大制動”。圖1中列車通過最大牽引達到最大巡航速度vcr,經過勻速巡航階段進入無動力惰行階段,在速度vbr時實施制動,直到在下一站停靠。
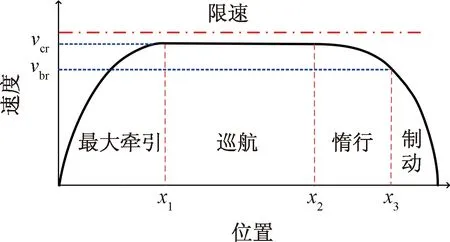
圖1 高速列車區間運行最優工況策略
1.2 高速列車多站間節能運行優化模型
考慮高速列車在連續站間的運行優化問題。列車從始發站s1出發,途中經過n個連續站間,最終達到終點站sn+1。在第i個區間內列車的運動過程可以表示為
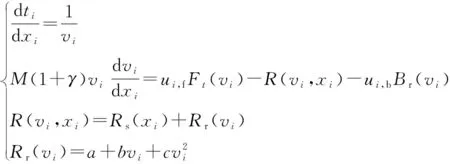
(1)
式中:xi∈[si,si+1],為在第i個區間內列車的位置;vi∈[0,vmax],為在第i個區間內列車的速度,vmax為當前位置最大限速;ti為第i個區間內列車的運行時間;M為列車的質量;γ為列車回轉質量系數;Ft(vi)和Br(vi)分別為列車在速度為vi時的最大牽引力和最大常用制動力,可由列車的牽引、制動特性確定;Rs(xi)、Rr(v)分別為列車行駛過程的線路阻力和基本阻力,基本阻力由速度決定;a,b,c為阻力系數;ui,f,ui,b∈[0,1]分別為牽引和制動系數,且和列車的運行狀態存在如下關系
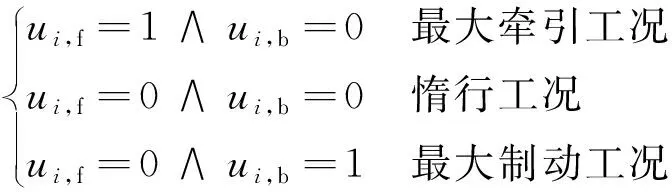
(2)
以CRH2A型高速動車組為例,列車的牽引、制動特性曲線見圖2。

圖2 CRH2A高速列車牽引、制動特性
為了實現計算機控制和處理,將距離進行離散化處理,對式(1)的微分項進行前向差分得到
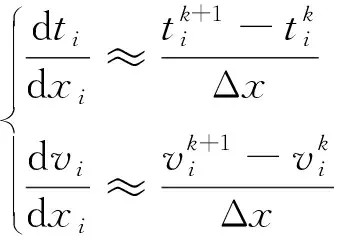
(3)
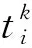
引入離散狀態空間的概念,將式(3)帶入式(1)中,以列車位置、速度和運行時間為狀態變量,可以得到表征高速列車動力學特征的非線性離散狀態空間模型為

(4)
根據圖1的最優駕駛策略,在區間i內,巡航速度vcr和制動初速度vbr把列車的運行過程分成了4種模式,因此決策變量vi=(vcr,i,vbr,i)確定了在該區間內列車的速度曲線。區間i包含的離散化子區間的個數Li可以通過式(5)得到,牽引、巡航、惰行和制動的子區間個數和決策變量相關,分別用Li,1,Li,2,Li,3,Li,4表示。
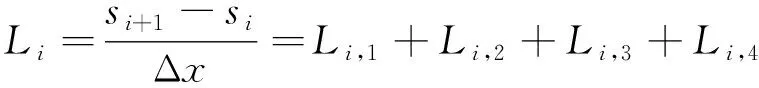
(5)
高速列車的制動方式包括空氣制動和電制動等,電制動又包含電阻制動和再生制動。如果制動產生的電能通過電阻發熱消耗掉,稱為電阻制動;如果制動產生的電能反饋給電網供其他設備使用,稱為再生制動。列車高速運行時優先使用再生制動,低速運行時以空氣制動為主[22],因此列車運行過程中的能耗主要來自牽引過程,本文在計算列車區間運行能耗時主要考慮牽引和巡航兩種工況下的運行能耗,因此由決策變量(vcr,i,vbr,i)確定的列車在區間i運行的能耗和運行時間可以表示為
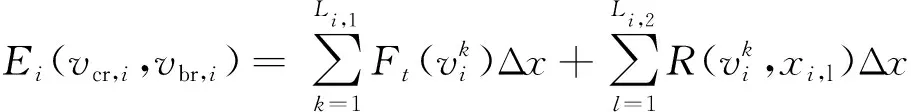
(6)

(7)
在整個解空間內,能耗和時間的范圍可以確定為Ei∈[Ei,min,Ei,max]和Ti∈[Ti,min,Ti,max]。綜合考慮能耗和時間,采用歸一化的思想,加權的目標函數可以表示為
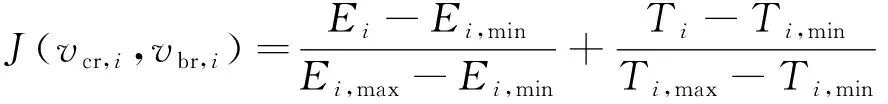
(8)
根據式(6)、式(7)和PSO-SA優化算法,可以得到區間i內,按照決策變量v=(vcr,i,vbr,i)建議的駕駛策略運行的能耗和時間見圖3。圖中每一個點代表一組可行的駕駛策略,也代表了一種可行的列車區間運行速度曲線。

圖3 Pareto曲線
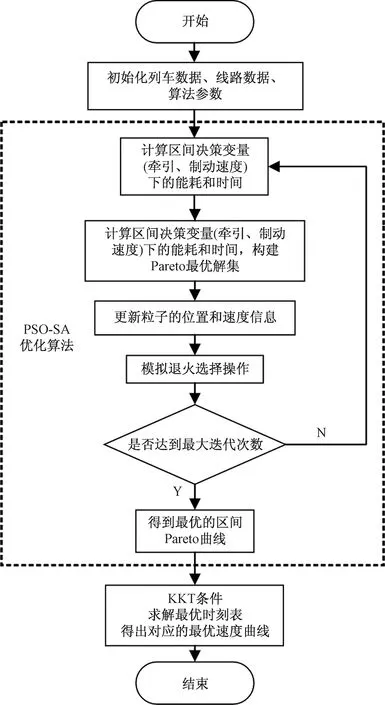
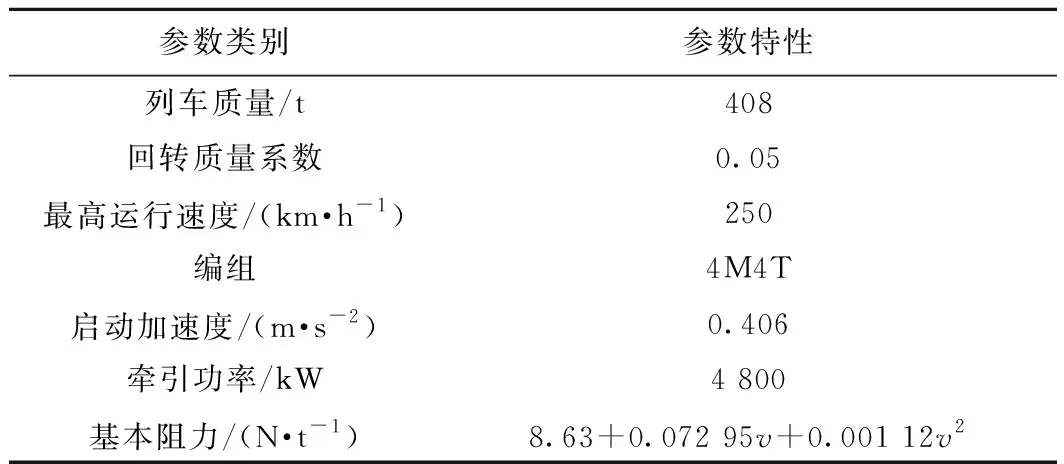
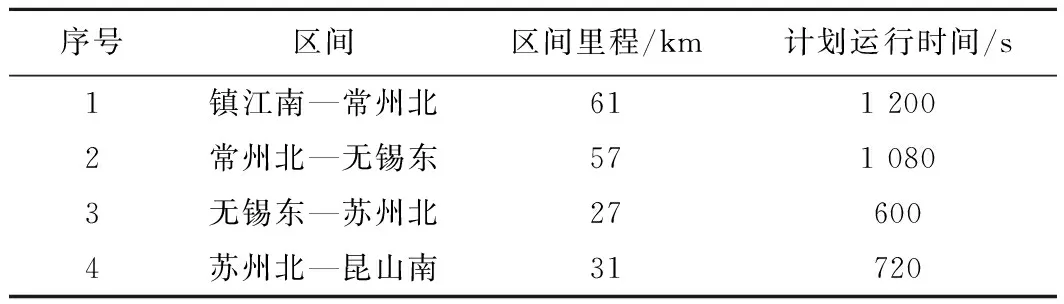
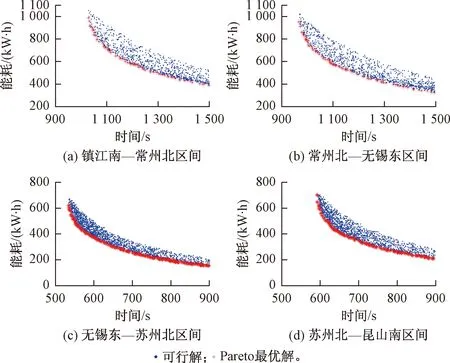
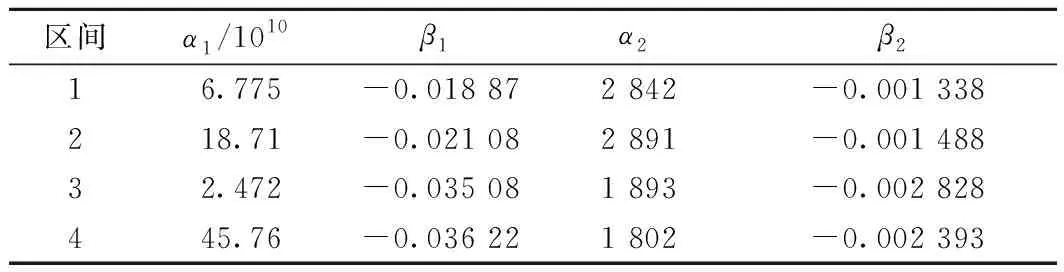
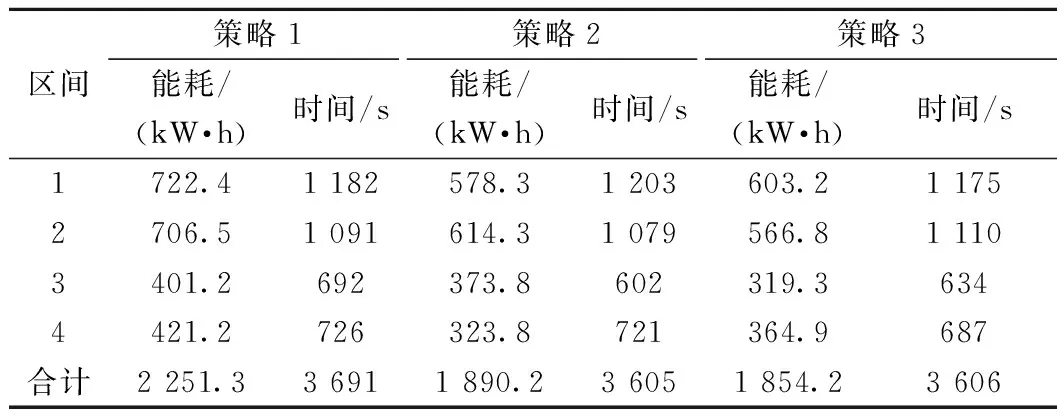
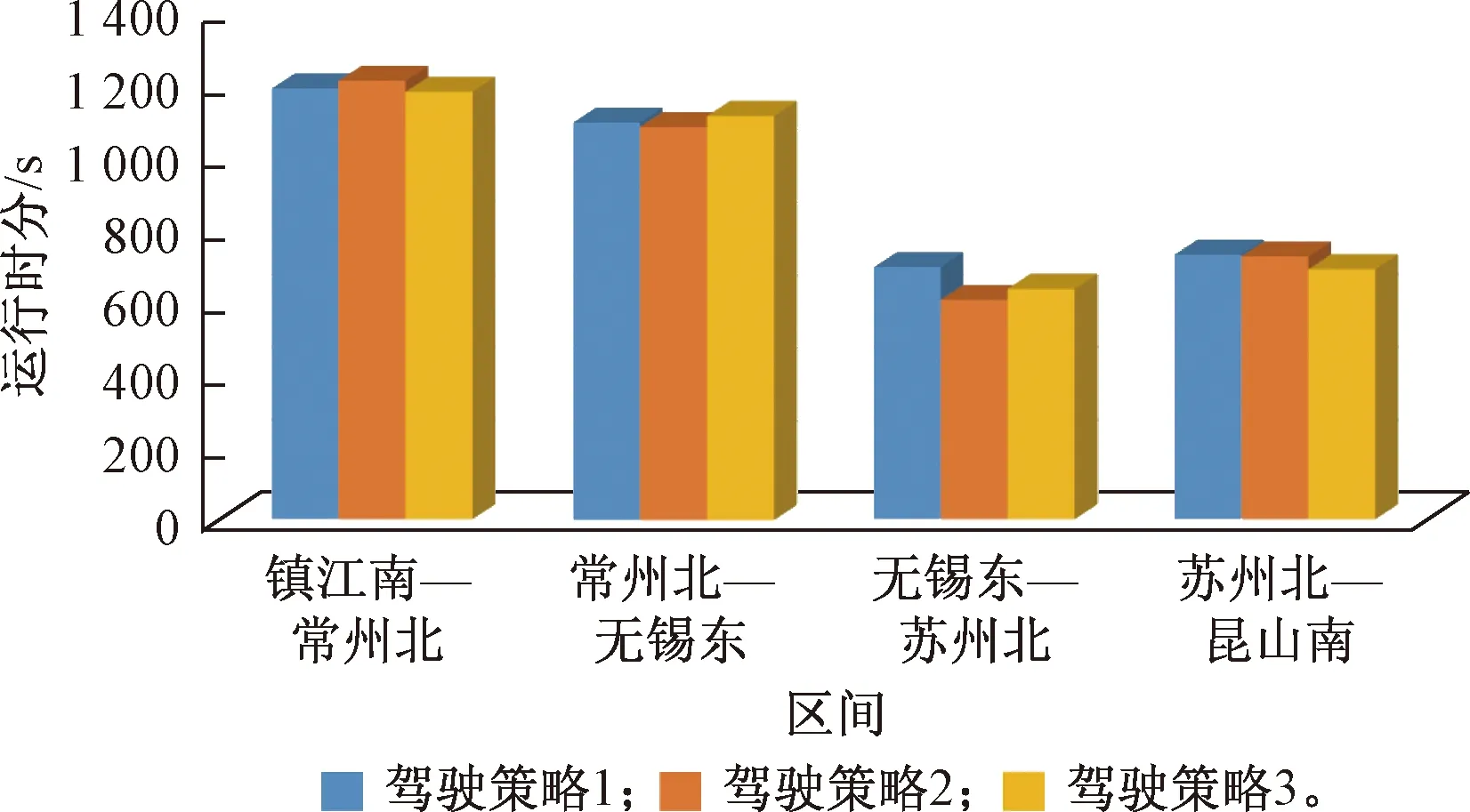
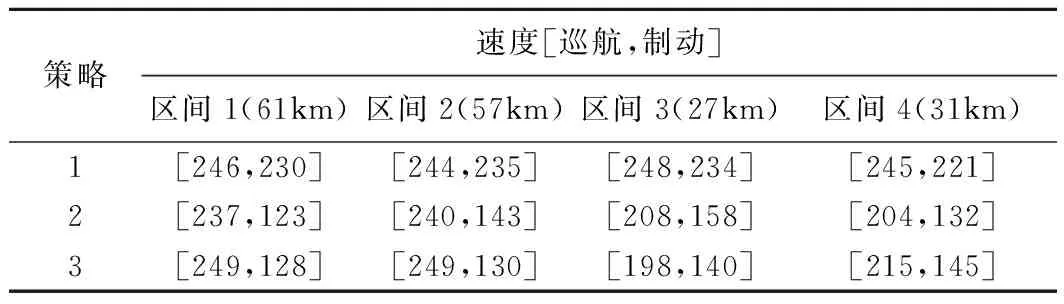
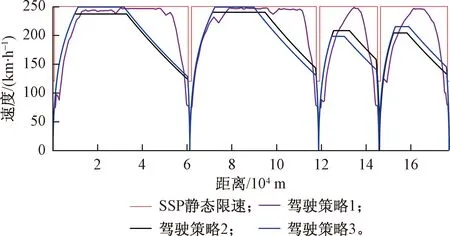
Pareto最優解根據多目標優化理論定義為:在可行空間Ω內,若對于任意的決策變量v∈Ω,不存在v*∈Ω,使得E(v*) 通過最小二乘法擬合逼近可以得到Pareto最優解集的區間運行能耗和時間的函數關系fi(·)。 Ei=fi(Ti) (9) 同理,可以得到列車在每個區間運行過程的最優解集的運行能耗和運行時間的擬合函數Ei=fi(Ti),i=1,2,…,n。因此,列車從始發站到終點站整個運行過程的節能優化問題可以表示為 (10) s.t.Ei=fi(Ti) Ti,min≤Ti≤Ti,max 式中:Tsch為全程多區間總運行時間;Ti,min和Ti,max分別為列車在區間i的最小運行時間和最大運行時間。 為了求解高速列車多站間運行節能優化問題,本文首先在粒子群PSO算法中引入模擬退火SA的思想,增強PSO算法的全局搜索能力,基于改進的PSO-SA算法求解列車單區間運行的以“能耗-時間”為指標的Pareto最優解集,并擬合得到Pareto曲線。根據KKT條件對多個區間列車運行時間進行優化匹配,得到基于時刻表調整的列車節能駕駛策略。 PSO算法是一種基于群體的隨機優化技術。每個可能的解都表示為種群的一個粒子,每個粒子都有自己的位置(決策變量)和速度(搜索方向),以及由目標函數決定的適應值,通過追隨當前搜索到的最優值來尋找全局最優值。SA算法是一種全局最優的隨機性組合優化方法,本文將SA算法引入粒子群的變異操作過程,使得算法在保留PSO算法簡單易實現的基礎上,提高全局搜索能力。算法的具體實現步驟如下: Step1初始化粒子種群Xg={X1,X2,…,XNP},g表示算法進化的代數,初始化時g=0,最大進化代數用gm表示,NP表示種群規模。其中第k個粒子Xk=(pk,dk)包含了粒子本身的位置信息pk和速度信息dk。位置信息pk=(vcr,vbr)由二維決策變量(巡航速度和制動初速度)確定,速度信息dk同樣是二維變量,決定了粒子每次迭代過程變化的步長,即粒子位置信息pk變化的大小。 (11) (12) 式中:ω為慣性權重;c1和c2為最優個體學習因子;r1和r2為相互獨立的偽隨機數,且服從[0,1]上的均勻分布。 Step4模擬退火選擇操作。首先計算更新前后粒子的適應度函數差值。 (13) 基于模擬退火過程計算每個粒子的接受概率為 (14) 式中:TPg為第g次迭代的退火溫度。基于模擬退火的選擇過程可以表示為 (15) 更新退火溫度,其中α為退火系數。 TPg+1=αTPg (16) Step5根據適應度函數的變化和最大進化代數判斷算法是否終止。隨著算法迭代計算,當種群的最優粒子適應度值不再變化或者當前進化代數滿足g≥gm時,算法迭代終止;未達到終止條件則返回Step 2。 根據2.1節的PSO-SA優化算法,可以得到列車在每個運行區間的Pareto最優解集。通過最小二乘法曲線擬合可以得到每個區間的能耗時間解析表達式。采用KKT條件求解式(10)描述的區間運行時刻表調整優化問題。 KKT條件是求解含有不等式約束的凸優化問題的充要條件,是一種擴展的拉格朗日乘子法。可將式(10)寫成標準的有不等式約束的優化問題為 (17) h1,j(Tj)=Tj,min-Tj≤0j=1,2,…,n h2,k(Tk)=Tk-Tk,max≤0k=1,2,…,n 式中:T=[T1T2…Tn]為列車各個區間運行時間的向量;g(·)為等式約束條件,表示列車從始發站至終點站總的運行時間固定;h1,j(·)和h2,k(·)為不等式約束條件,分別表示每個區間運行時間的下限約束和上限約束。 本文采用指數函數來擬合能耗時間存在的解析關系,即函數fi(·)為指數函數的線性組合,是典型的凸函數。同時約束條件g(·)、h1,j(·)和h2,k(·)都是具有仿射性的函數,因此式(17)表示的含有不等式約束的優化問題是凸優化問題,可以采用KKT條件求解。 定義含有不等式約束條件的拉格朗日函數為 (18) 式中:參數λ、u1、u2為相應約束條件的乘子。 因此,根據KKT條件可以得到時刻表調整優化問題的求解方案,即 (19) 其中,微分項?L/?Ti=0用來求解函數的極值點;在KKT條件中等式約束的乘子λ不能為零,不等式約束的乘子u1,j、u2,k需要滿足非負性;同時經過乘子作用的約束項λg(T)、u1,jh1,j、u2,kh2,k必須等于零才可以保證拉格朗日函數和原優化函數等價。 由KKT條件,可以得到最優的節能運行時刻表T*,也就確定了列車每個運行區間最佳的巡航速度和制動初速度,從而得到優化的列車區間運行速度曲線。基于時刻表調整的列車駕駛節能優化方法流程見圖4。 圖4 算法流程 為了驗證基于時刻表調整的列車駕駛節能優化方法的有效性,以2015年1月D3096次動車組在全長176 km的區段實際運行數據為依據進行仿真測試,該區段共包含5個連續車站,共4個區間:鎮江南—常州北—無錫東—蘇州北—昆山南。列車和各區間的基本參數如表1、表2所示。 表1 CRH2A型列車主要參數 表2 鎮江南—昆山南區間運行信息 根據2.1節的PSO-SA算法,求解每個區間的最優的巡航速度和制動初速度,得到以能耗和時間為指標的Pareto最優解集,結果見圖5。根據最優解集可以看出區間能耗和時間之間存在明顯的負相關關系。本文采用了指數函數來表征每個區間能耗-時間之間的擬合函數關系,具體的函數表達式為 Ei=fi(Ti)=α1eβ1Ti+α2eβ2Ti (20) 式中:α1、β1、α2、β2為擬合參數。 圖5 區間Pareto最優解 圖6給出了每個區間基于最小二乘法的Pareto擬合曲線。4個區間的擬合結果如表3所示。 圖6 “能耗-時間”擬合曲線 區間α1/1010β1α2β216.775-0.018 872 842-0.001 338218.71-0.021 082 891-0.001 48832.472-0.035 081 893-0.002 828445.76-0.036 221 802-0.002 393 在擬合能耗-時間Pareto曲線基礎上,根據式(19)所列的KKT條件,得到時刻表的最優調整策略和優化后的列車站間運行時分。表4給出了列車實際駕駛策略、準點最優駕駛策略和基于時刻表調整的最優駕駛策略的區間運行能耗和運行時間的分析。實際駕駛策略(策略1)以列車車載設備實測記錄數據和《列車牽引計算規程》[23]作為依據;準點駕駛策略(策略2)采用本文提出的PSO-SA優化算法求得,在滿足準點的基礎上實現最節能駕駛,即在圖6擬合曲線上搜索最接近準點要求的最優解;基于時刻表調整的最優駕駛策略(策略3)是在本文PSO-SA優化算法的基礎上,采用KKT條件求解,得出時刻表調整后的最節能駕駛策略。根據表4可以看出,基于PSO-SA算法的準點駕駛策略相比實際列車運行策略,能耗降低了16%;基于時刻表調整的最優駕駛策略在準點駕駛策略的基礎上能耗降低了1.9%,優化前后的列車區間運行時分見圖7。 表4 3種駕駛策略區間運行結果 圖7 區間運行時分 優化前后每個區間的巡航速度和制動初速度如表5所示,圖8給出了相應的三種駕駛策略的速度曲線。可以看出相對于駕駛策略1而言,駕駛策略2在按照既有時刻表運行的條件下增加了惰行工況時間來減少區間運行能耗;同時對于站間距較短的區間(區間3和區間4),由于較大的巡航速度會導致較早的制動,所以本文的優化方法減小了站間距較短的區間巡航速度,有效地降低了列車的運行能耗。駕駛策略3基于站間的運行時間匹配,調整列車運行時刻表,可以在駕駛策略2的基礎上進一步減少列車運行能耗。結果表明,和列車實際駕駛策略相比,結合PSO-SA算法和KKT條件調整時刻表后的最優駕駛策略可以降低17.6%的站間運行能耗。 表5 區間巡航速度和制動初速度 km/h 圖8 三種駕駛策略速度曲線 本文針對高速列車在連續站間運行的節能優化問題,建立了表征高速列車動力學特征的非線性離散狀態空間模型和高速列車節能駕駛策略優化模型;采用基于模擬退火的粒子群算法求解最優的區間運行策略,得到以區間運行能耗和運行時間為目標的Pateto最優解,利用 KKT條件求解最佳的站間運行時分組合;本文以高速列車在鎮江南—昆山南連續站間的運行數據為基礎進行仿真測試。仿真結果表明,通過增加惰行工況運行時間和優化站間運行時間可以有效地實現最優化節能駕駛。本文的研究結果可以為列車運行區間巡航速度的選擇、惰行工況的利用和連續站間時刻表優化提供參考。 本文僅考慮了單車在連續站間運行的節能優化問題,隨著客流量的增大和發車間隔的減小,多車追蹤運行情況下的相互影響和再生制動能耗的利用是今后研究的方向。
2 高速列車節能運行優化方法
2.1 基于PSO-SA算法的區間運行優化過程
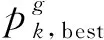

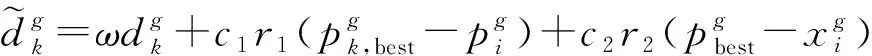
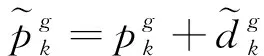
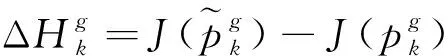

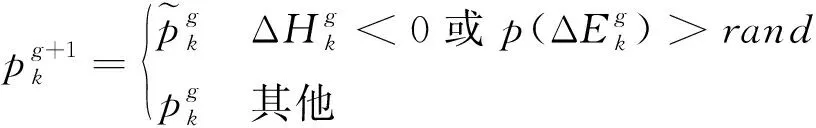
2.2 基于KKT條件的時刻表調整優化
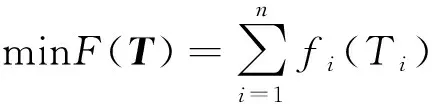
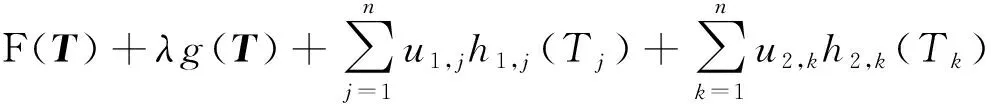
3 仿真驗證結果分析

4 結束語

