Robin邊界條件下非線性算子方程的變號解
張強
Robin邊界條件下非線性算子方程的變號解
張強
濰坊科技學院通識學院, 山東 濰坊 262700
為探索在Robin邊界條件下非線性算子方程變號解,本文通過非線性算子方程變號解的穩定性分析,尋找變號解的對稱廣義中心平衡點,建立Jacobi數學模型進行穩定譜特征點檢測,并在Dirichlet邊值條件下進行奇異特征解分析,采用擾動加權方法進行Robin邊界條件下非線性算子方程的臨界穩態性分析,證明其約束泛函臨界值的存在性和穩定性。建立非線性算子方程Caffarelli-Kohn-Nirenberg變號約束相關性條件,計算非線性算子方程的變號解滿足的邊界條件,構建Robin邊界條件下Sobolev和Hardy臨界擴展約束算法,實現對非線性算子方程變號解準確計算和漸進穩定性證明。
Robin邊界條件; 非線性算子方程; 變號解
非線性方程廣泛用于描述非線性動力學模型和物理學模型,Robin邊界條件下非線性算子方程對于實際的控制數學和應用數學具有很好的描述,在Robin邊界條件約束下分析非線性算子方程的變號解,根據變號解的穩定性進行控制系統的收斂性約束分析,Robin邊界條件非線性算子方程的解不論是對于理論的數學分析,還是實際的數學應用來說都具有重要的意義[1]。Robin邊界條件非線性算子方程中的解具有變號性,受到符號約束的穩態特性的影響,導致方程的解向量存在穩態誤差,在Robin邊界條件下無法解出正確的變號解。
對此,本文研究一種優化的Robin邊界條件下非線性算子方程變號解分析方法[2],在某些不確定的條件下,根據Robin邊界條件下非線性算子方程變號解的發散特征量,進行約束性關聯分析,采用穩態特征收斂模型計算Robin邊界條件下非線性算子方程變號解的穩定性,結合判決和門限準則,在Dirichlet邊值條件下進行非線性算子方程的奇異特征解分析,采用擾動加權方法進行Robin邊界條件下非線性算子方程的臨界穩態性分析,采用馬爾尼數鏈隨機分析模型,進行邊界收斂性判斷,求得Robin邊界條件下非線性算子方程的變號解,建立非線性算子方程Caffarelli-Kohn-Nirenberg變號約束相關性條件,計算非線性算子方程的變號解滿足的邊界條件[3],構建Robin邊界條件下Sobolev和Hardy臨界擴展約束算法,實現對非線性算子方程變號解準確計算和漸進穩定性證明。經過Robin邊界條件使得目標函數收斂于最優解,論文從理論和數學推導上進行和變號解的穩定性和有限收斂性驗證。
1 非線性算子方程數學模型構建與問題描述
1.1 非線性算子方程數學模型及引理
在非線性微分方程發展的過程中,需要分析Robin邊界條件下非線性算子方程的變號解,結合變號解的穩定性和收斂性進行非線性動力學分析,建立穩態收斂的數學控制模型[4],并應用在動力學控制中,定義Robin邊界條件非線性微分方程的正多解:→R的>0階Dirichlet邊值特征解向量為:
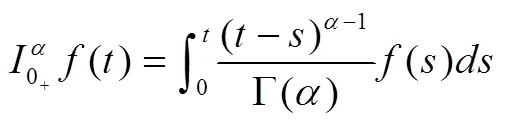
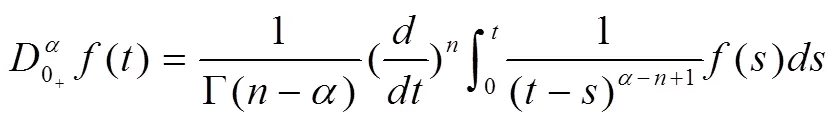
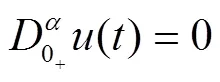
存在非齊次邊界條件下[6],有唯一變號解:
其中:為非線性算子方程中變號解取得的整數值,取值要求為大于或等于的整數,使得方程具有廣義隨機收斂性[7]。
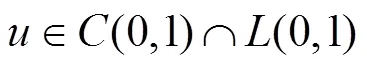
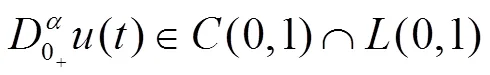
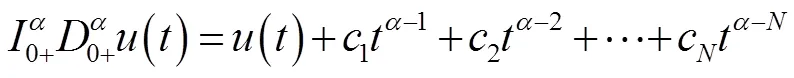
1.2 Robin邊界約束條件
在Jacobi數學模型中進行非線性算子方程的穩定譜特征點檢測,在Dirichlet邊值條件下進行非線性算子方程的奇異特征解分析[9]。
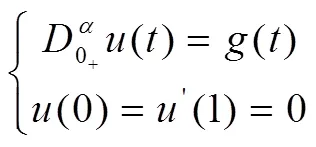
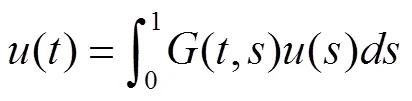

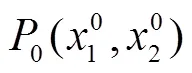
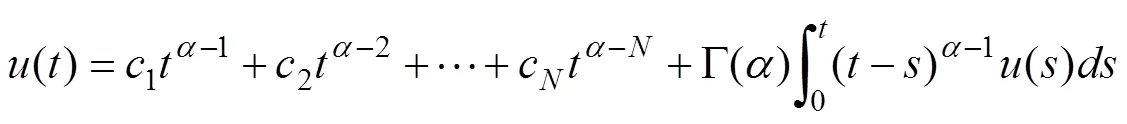
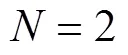
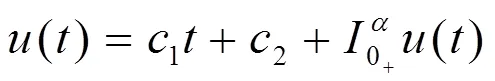
且:
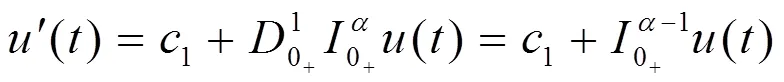
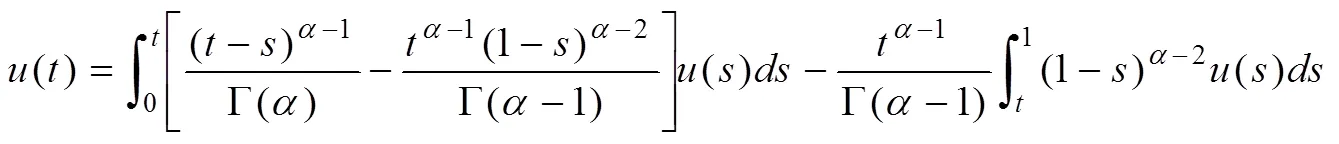
綜上分析,采用擾動加權方法進行Robin邊界條件下非線性算子方程的臨界穩態性分析,求得方程的變號解,結合非線性算子方程的變號解分析結果進行穩態收斂性證明。
2 非線性算子方程的變號解及穩定性分析
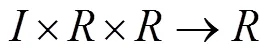
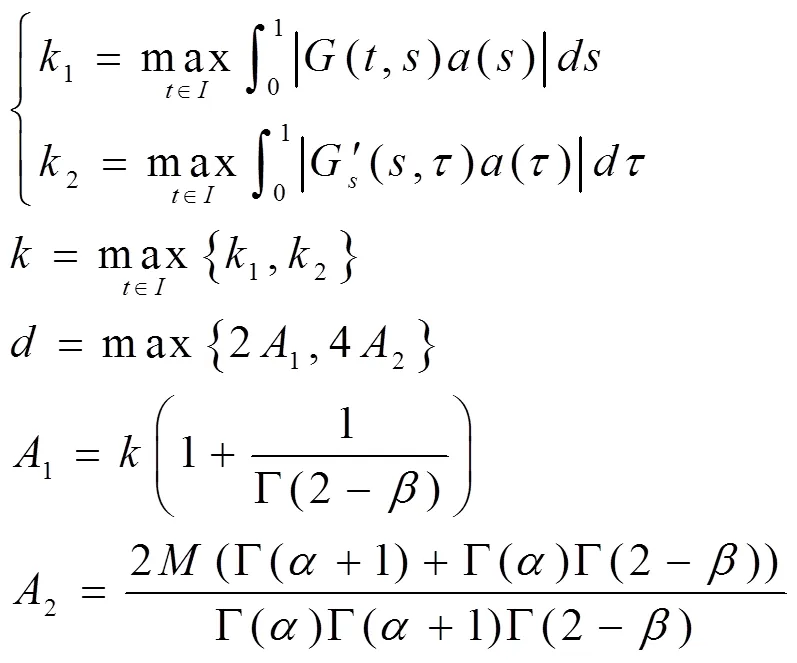
證明
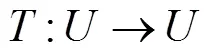
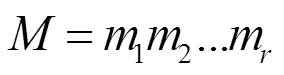
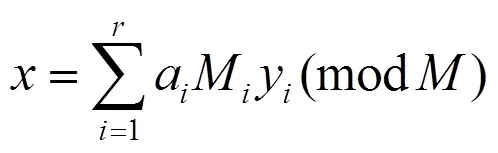
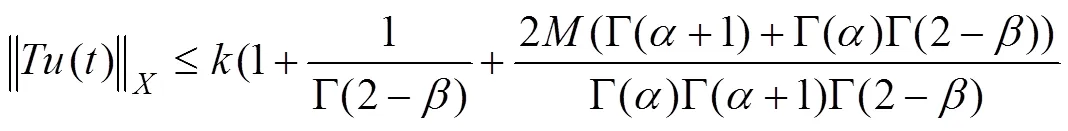
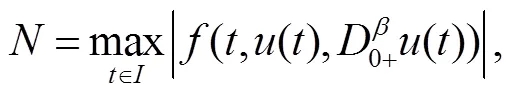
結合約束性關聯分析,在Robin邊界條件下非線性算子方程的聯合有界特征量為:
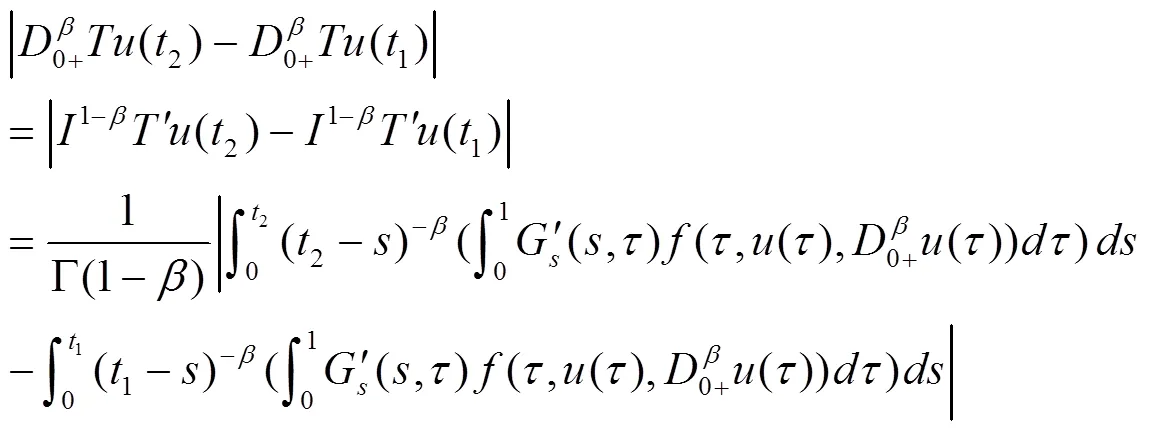
從而可以推導得到:
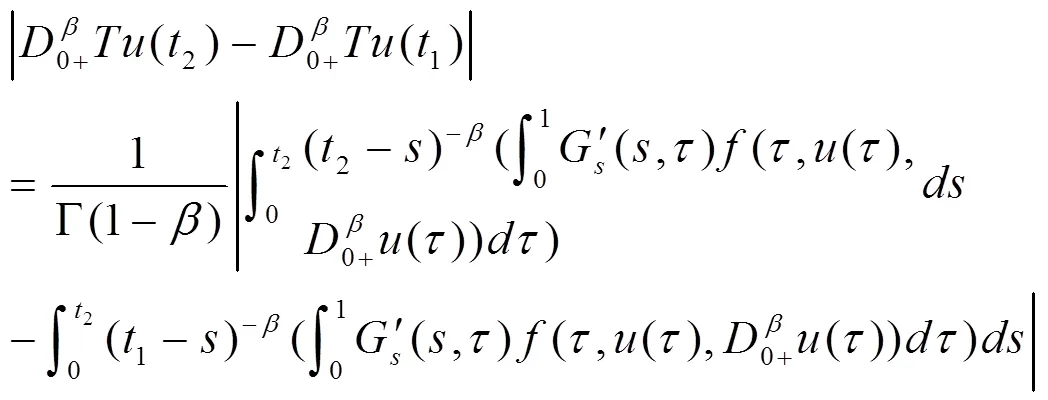
通過建立非線性算子方程Caffarelli-Kohn-Nirenberg變號約束相關性條件,得到如下結論:
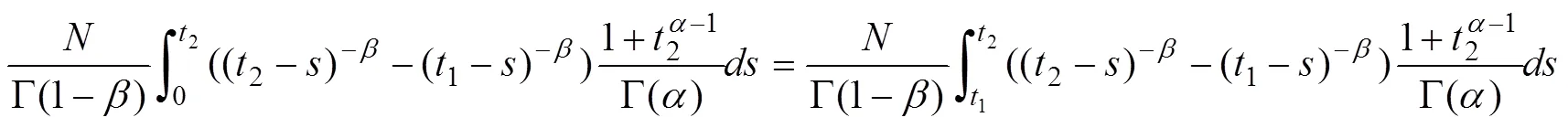
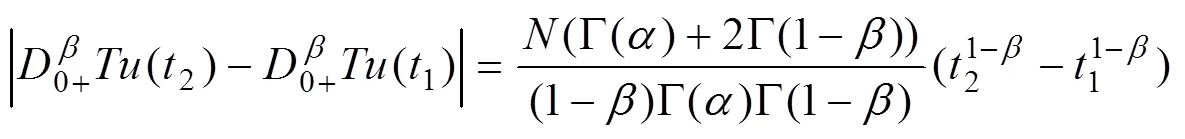
可見,計算得到的Robin邊界條件下非線性算子方程變號解是穩態收斂,命題得證。
3 數值分析
通過數值分析的方法測試Robin邊界條件下非線性算子方程變號解分析問題,采用SPSS14.0作為分析軟件,進行數值分析,數值樣本采樣隨機序列樣本,樣本數據的規模為2000,測試集為200,訓練集為100,迭代次數為1024,根據上述測試參數設定,進行非線性算子方程變號解分析,得到測試樣本數據見表1。
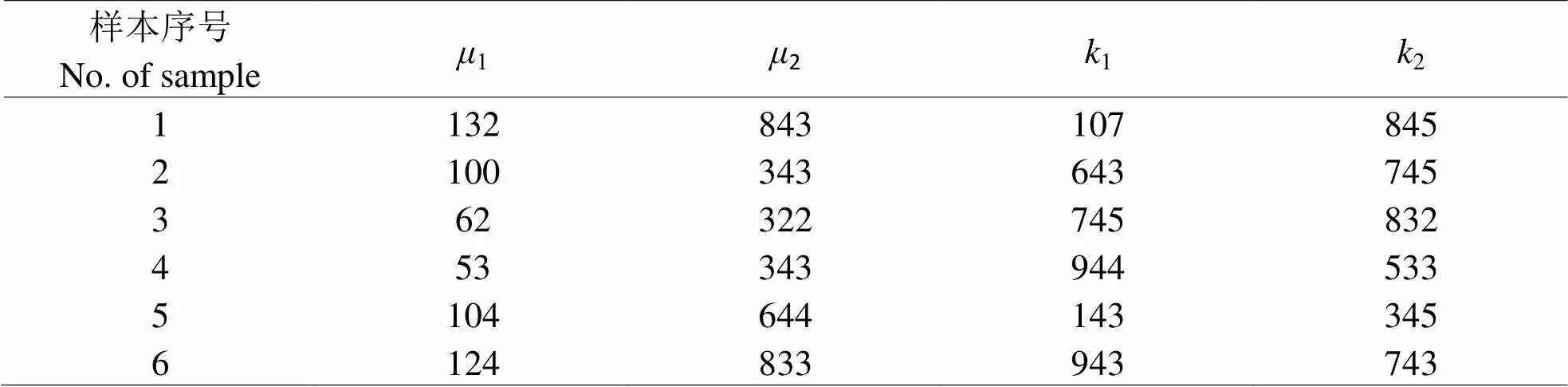
表1 測試樣本數據
將上述測試數據通過最小二乘擬合方法輸入到系統中,分析Robin邊界條件下非線性算子方程變號解問題,使用傳統方法分析用得到結果如表2描述。
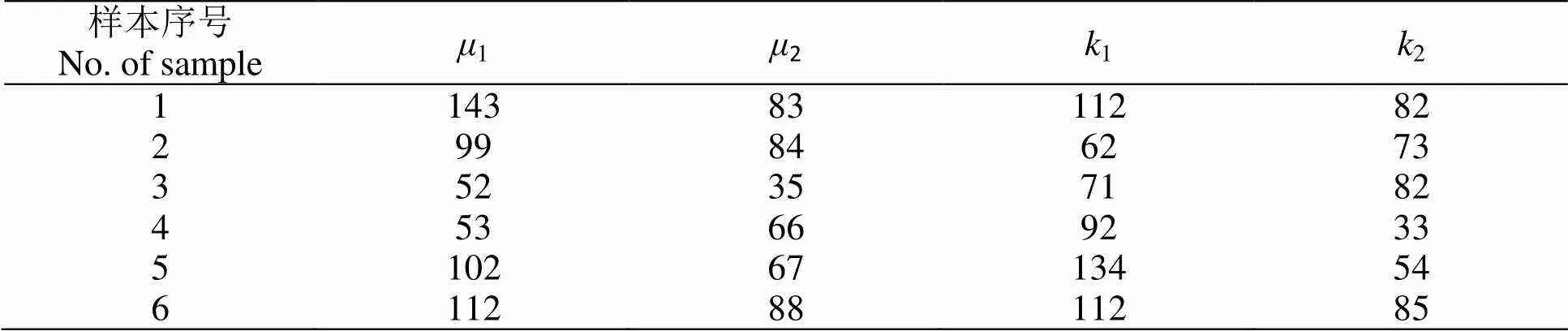
表2 傳統算法分析數據
使用本文算法分析Robin邊界條件下非線性算子方程變號解參數用表3描述:
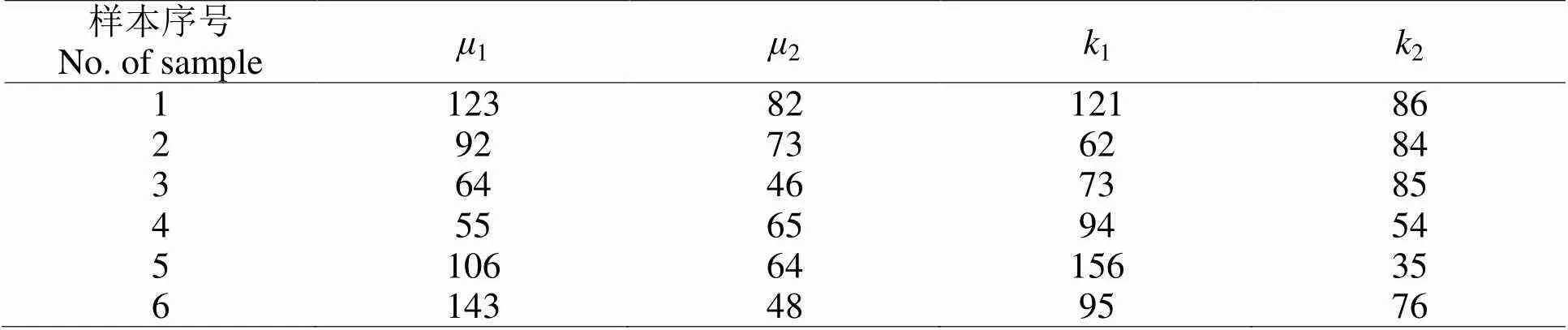
表3 本文算法分析數據
分析上述測試結果得知,本文方法進行Robin邊界條件下非線性算子方程變號解分析的擬合效果較好,收斂性較強,并應用在控制系統中,得到控制性能曲線對比如圖1所示,分析圖1得知,本文方法進行Robin邊界條件下非線性算子方程變號解優化求解,提高了收斂性和全局穩定性。
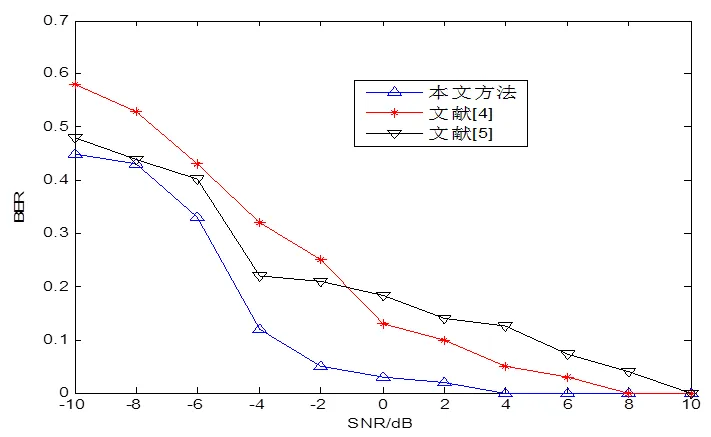
圖1 性能對比
4 結語
本文研究在Robin邊界條件下非線性算子方程變號解問題,結合非線性算子方程變號解的穩定性分析,提高非線性控制系統的穩定性。計算非線性算子方程變號解在對稱廣義中心的穩定性平衡點,建立Jacobi數學模型進行非線性算子方程的穩定譜特征點檢測,在Dirichlet邊值條件下進行非線性算子方程的奇異特征解分析,采用擾動加權方法進行Robin邊界條件下非線性算子方程的臨界穩態性分析,證明非線性算子方程的約束泛函臨界值的存在性和穩定性,建立非線性算子方程Caffarelli-Kohn-Nirenberg變號約束相關性條件,計算非線性算子方程的變號解滿足的邊界條件,構建Robin邊界條件下Sobolev和Hardy臨界擴展約束算法,實現對非線性算子方程變號解準確計算和漸進穩定性證明。本文方法對非線性算子方程變號解分析的擬合效果較好,收斂性較強。
[1] 李盼曉.非局部時滯反應擴散方程波前解的指數穩定性[J].應用數學和力學,2018,39(11):1300-1312
[2] 李遠飛.Robin邊界條件下更一般化的非線性拋物問題全局解的存在性[J].應用數學學報,2018,41(2):257-267
[3] Wang X. Green functions for a decagonal quasicrystalline material with a parabolice boundary[J]. Acta Mechanica Solida Sinica, 2005,18(1):57-62
[4] Liu Y, Luo SH, Ye YH. Blow-up phenomena for a parabolic problem with a gradient nonlinearity under nonlinear boundary conditions[J]. Computers and Mathematics with Applications, 2013,65:1194-1199
[5] 都琳,張瑩,胡高歌,等.一種雙寡頭壟斷Cournot-Puu模型的混沌控制研究[J].應用數學和力學,2017,38(2):224-232
Sign Variation Solution of Nonlinear Operator Equation under Robin Boundary Condition
ZHANG Qiang
262700,
To explore the sign variation solution of nonlinear operator equation, this paper established Jacobi mathematical model to look for an equilibrium point of symmetric generalized center of the variable sign solution, the Jacobi model was established to detect the stability spectrum characteristic point of nonlinear operator equation and The singular characteristic solution of nonlinear operator equation was analyzed under Dirichlet boundary value condition, and the critical steady-state of nonlinear operator equation with Robin boundary condition was analyzed by perturbation weighting method. This paper proved the existence and stability of the critical value of constrained functional of nonlinear operator equations, established the constraint correlation conditions of nonlinear operator equations with Caffarelli-Kohn-Nirenberg variation sign, and calculated the boundary conditions satisfied by the variation solutions of nonlinear operator equations. The critical extended constraint algorithms of Sobolev and Hardy under Robin boundary conditions were constructed, and the exact calculation of the signed solutions of nonlinear operator equations and the proof of asymptotic stability were realized.
Robin boundary condition; nonlinear operator equation; sign change solution
O211.62
A
1000-2324(2019)05-0893-05
10.3969/j.issn.1000-2324.2019.05.035
2018-06-04
2018-10-12
山東省教育科學“十二五規劃”高等教育數學專項課題(CBS15001)
張強(1980-),男,碩士,講師,研究方向為計算數學. E-mail:zhangqiang55@126.com

