永磁同步電機自適應模糊滑模魯棒無源控制

張懿 韋漢培 魏海峰 儲建華 彭艷

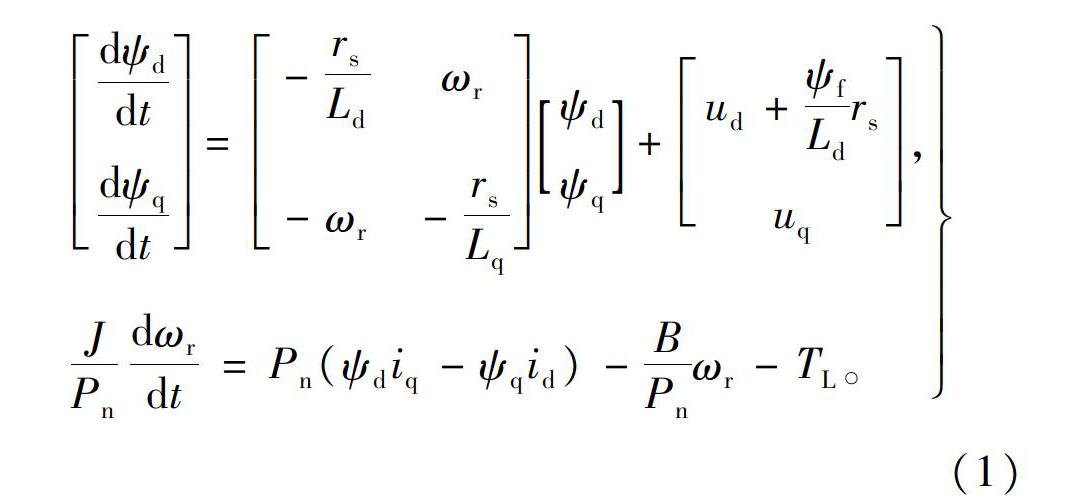
摘要：針對傳統永磁同步電機滑模控制存在的抖振以及系統魯棒性差問題，提出基于自適應模糊滑模軟切換的永磁同步電機魯棒無源控制方法。控制系統電流內環通過設計魯棒無源控制器，得到dq旋轉坐標系下的電壓給定，有效提高電流預測控制的魯棒性。轉速外環設計模糊滑模軟切換控制器，利用雙曲正切函數代替符號函數，實現軟切換連續控制。采用自適應模糊控制法估計集成不確定邊界，有效削弱滑模抖振。實驗對比傳統滑模控制與新型控制方法，其結果驗證了新型控制方法在抖振以及抗擾動方面的有效性和實用性。

關鍵詞：永磁同步電機;自適應模糊滑模;無源控制;滑模控制;魯棒性

DOI：10.15938/j.emc.2019.09.013

中圖分類號：TM 301

文獻標志碼：A

文章編號：1007-449X（2019）09-0101-07

Adaptive fuzzy sliding mode robust passive control of ?permanent magnet synchronous motor

ZHANG Yi1，2，WEI Han?pei1，2，WEI Hai?feng1，2，CHU Jian?hua2，PENG Yan3

（1.Institute of Electronics and Information，Jiangsu University of Science and Technology， Zhenjiang 212000，China;

2.Jiangsu Kai Xuan Intelligent Technology Co.， Ltd， Suzhou 215000， China;

3.School of Mechatronic Engineering and Automation，Shanghai University，Shanghai 200444，China）

Abstract：

Traditional sliding mode control（SMC）of permanent magnet synchronous motor （PMSM） has buffeting problem， and its robustness is poor. In view of this problem， a robust passive control method for PMSM based on adaptive fuzzy sliding mode soft switching was proposed. Through the design of robust passive controller， the internal current loop of the control system was given in the voltage under dq rotating coordinate system， then the current predictive control robustness was improved effectively. In out speed loop， fuzzy sliding mode soft switching controller was designed， and the hyperbolic tangent function was used instead of symbolic function， then the soft switching continuous control was achieved. Adaptive fuzzy control method was used to estimate the uncertain boundary， and the sliding mode buffeting was reduced effectively. Compared with the traditional SMC and the new control method， the experimental results verify the effectiveness and practicability of the new control method in buffeting and perturbation.

Keywords：permanent magnet synchronous motor; adaptive fuzzy sliding mode;passive control; sliding mode control;robustness

0引言

永磁同步電機具有結構簡單、效率高、功率密度高等固有優點，在電動汽車、風力發電、機器人等各種工業領域中得到了廣泛的應用。永磁同步電機的控制系統通常采用磁場定向控制，該控制系統結構為一個具有內電流環和外轉速環的串級控制結構，傳統的PI控制技術由于其實現簡單，在內電流環和外轉速環中仍然較受歡迎。然而，實際的永磁同步電機系統中存在著大量的內部或外部干擾和不確定性，如未建模動力學、參數變化、摩擦力和負載干擾。傳統的線性控制方法，如PI控制，難以取得較好的控制效果。

為此，在具有內外擾動和不確定性的永磁同步電機系統中，多種非線性控制方法被采用來提高系統的控制性能，如魯棒控制、滑模控制、無源控制、反步控制等。在這些非線性控制方法中，滑模控制方法以其對內部參數攝動和外部干擾的魯棒性而聞名，其可保證在參數或模型不確定性的情況下保持良好的跟蹤性能。文獻針對永磁同步電機的速度環控制，提出了一種基于新型趨近律的滑模控制方法，減小了系統的抖振，同時設計了一種滑模觀測器來估計系統的擾動，提高了系統的魯棒性。文獻將滑模控制應用于永磁同步電機的電流環控制，以實現精確的電流跟蹤性能。文獻設計了一種滑模觀測器來估計永磁同步電機電流控制的參數變化和模型不確定性。眾所周知，抖振是滑模控制的主要缺點。為了削弱這種現象，眾多文獻采用邊界層積分滑模控制技術對永磁同步電機進行速度控制。隨著滑模控制理論的發展，文獻提出了一種末端滑模速度控制器，通過選擇合適的趨近律，將非線性項引入滑模控制中，有效削弱了系統抖振，提高了系統收斂速度。但是，設計的電機控制器首先采用串級控制結構，與內部電流回路相比，外部速度回路具有相對較慢的瞬態響應。文獻提出了一種新的指數趨近律來設計速度和電流控制器。為了抑制系統抖振，系統變量被應用于該趨近律。然而，在上述趨近律中，由于滑模面函數的變化，使得不連續增益迅速減小，從而降低了滑模面附近控制器的魯棒性，同時也增大了系統收斂時間。

為有效削弱傳統滑模控制存在的固有抖振，以及增強控制系統魯棒性，給出一種基于自適應模糊滑模軟切換的永磁同步電機魯棒無源控制方法。電流內環通過設計魯棒無源控制器，提高電流預測控制的魯棒性。轉速外環設計模糊滑模軟切換控制器，有效削弱滑模抖振。實驗結果驗證了新型控制方法在抖振及抗擾動方面的有效性。

1魯棒無源控制器設計

隱極式永磁同步電機在d-q旋轉坐標系下的數學模型為

dψddt?dψqdt=-rsLdωr?-ωr-rsLqψd?ψq+ud+ψfLdrs?uq，

JPndωrdt=Pn（ψdiq-ψqid）-BPnωr-TL。（1）

式中：ψd、ψq為電機定子磁鏈在d、q軸上的分量;ud、uq和id、iq為電機定子電壓、電流在d、q軸上的分量;ωr為電機轉子電角速度;ψf為電機轉子給定磁鏈;Pn為極對數;rs為電機定子電阻;Ld、Lq為電機定子d、q軸電感。對于隱極式（表貼式）轉子永磁同步電機而言，由于轉子給定磁場氣隙均勻，定子繞組電感值與轉子位置無關，定子繞組電感在d、q軸上的分量相同，即Ld=Lq=L，TL為電機負載轉矩，B、J為電機輸出軸摩擦阻力系數和轉動慣量。令

D=diagLLJP2n，

Dx=ψd-ψfψqJP2nωrT=

D[idiqωr]T，

u=[uduq]T，

y=[idiq]T。（2）

則系統狀態方程可表示為

Dx·=-rs0ψq?0-rs-ψd?-ψqψd-BP2nid?iq?ωr+

10?01?00ud?uq+0?0?-1PnTL，

y=[idiq]T。（3）

根據式（2）和式（3），將式（1）永磁同步電機dq旋轉坐標系下的數學模型推導出無源控制模型為

Dx·=[J（x）-R（x）]x+g（x）u+ζ，

y=gT（x）x。（4）

式中：J（x）=00ψq?00-ψd?-ψqψd-BP2n，u=[uduq]T，g（x）=10?01?00，ζ=0?0?-1PnTL，R（x）=rs00?0rs0?000，x=[idiqωr]T。

并且J（x）為反對稱矩陣，J（x）=-JT（x），其反映了該系統內部的互聯結構。R（x）為半正定對稱矩陣，其反映了端口上的附加阻性結構。

定義狀態誤差向量E=x-x*，其中x*為系統期望向量，即給定向量值;x代表實際向量。將狀態誤差向量E帶入式（4）無源控制模型，得到系統狀態誤差模型為

DE·-[J（x）-R（x）]E=-Dx·+[J（x）-R（x）]x*+g（x）u+ζ。（5）

取誤差能量函數為

HE=12ETDE。（6）

對其進行求導，得到

H·E=-ETRE+ETφ。（7）

式中φ=-Dx·*+[J（x）-R（x）]x*+g（x）u+ζ。

為保證系統快速的動態性能，向其注入阻尼，加速能量耗散，令φ=-RaE。式（7）變換為

H·E=-ET（R+Ra）E。（8）

式中：Ra=diag{Ra1，Ra2，Ra3}為正定對角矩陣，當系統存在擾動時，誤差狀態方程表示為

DE·-[J（x）-R（x）]E=-Dx·*+[J（x）-R（x）]x*+g（x）u+ζ+ζ。（9）

對HE沿式（9）誤差軌跡求導得

H·E=-ETRE+ETφ+ETξ。（10）

為抑制擾動誤差，設計φ=-RaE+χ，則

H·E=-ET（R+Ra）E+ET（χ+ξ）。（11）

式中：χ=[χ1χ2]，選擇合理的χ值，滿足ET（χ+ξ）≤0，則H·E<0，誤差漸近收斂于零。根據φ=-RaE+χ求得魯棒無源控制器的輸出dq軸給定電壓為

ud=-ψdω*r-Ra1id+χ1，

uq=（L+rs）i*q-Ra2（iq-i*q）+ψdω*r+χ2。（12）

2自適應模糊滑模控制器設計

考慮不同工況下的電機參數攝動，永磁同步電機運動方程為

ω·r+（a+a）ωr+（d+d）=（b+b）iq。（13）

式中：a=BJ，b=P2nJψf，d=PnJTL，a，b以及c為電機參數攝動量。

定義電機轉速跟蹤誤差e（t）=ωr（t）-ω*r（t），其中ωr（t）為永磁同步電機實際轉速，ω*r（t）為給定電機轉速。由此得到動態方程為

e·（t）=-ae（t）+w（t）+f（t）。（14）

式中：w（t）=biq-aω*r（t）-d-ω·*r（t），f（t）=-aω^r（t）-d+biq。

為有效減小穩態誤差，選擇以轉速跟蹤誤差e為自變量的積分型滑模面為

s=e+k∫10e（τ）dτ。（15）

對式（15）求導得

s·=e·+ke=-ae（t）+w（t）+f（t）+ke（t）。（16）

令 s·=0，f（t）=0，得到滑模等效控制ueq表達式為

ueq=1b[（a-k）e（t）+aω*r（t）+d+ω·*r（t）]。（17）

為有效增強系統抗參數攝動以及外部負載擾動的魯棒性，進一步改善抖振問題，采用雙曲正切函數軟切換控制器

ubc=-htanh（s）。（18）

控制器輸出（q軸電流給定）為

u=i*q=ueq+ubc。（19）

定義Lyapunov函數為

v=12s2。（20）

對其求導得

v·=ss·=s[-ae（t）+w（t）+f（t）+ke（t）]=

s[-bhtanh（s）+f（t）]=

-bh|s|+f（t）s≤-|s|（bh-|f（t）|）。（21）

選取合適的雙曲正切函數軟切換控制器增益h，滿足bh>|f（t）|，則v·<0，系統穩定。

h參數的選取使用模糊推理法，將模糊控制器的輸入量s、s·和輸出量h進行歸一模糊化，記為s～、s～·和h～。其論域規劃為和。取s～和s·模糊語言值為{N（負），Z（零），P（正）}，h模糊語言值為PS（正小），PM（正中），PB（正大）}。設計隸屬度函數為高斯型隸屬函數，采用Mamdani模糊推理，模糊控制規則設計為表1所示。

使用重心法對模糊輸出h進行反模糊計算

h=∑Ni=1piμi（s～）μi（s～·）∑Ni=1μi（s～）μi（s～·）=pTw（s）。（22）

式中：w（s）=[w1（s）w2（s）…wn（s）]T，

p=[p1，p2…pn]T，

wi（s）=μi（s～）μi（s～·）∑Ni=1μi（s～）μi（s～·）。

假設h*為h的最優值選取，采用自適應律p·=βb|s|w來調節h*值，系統漸近穩定。

證明：

設計自適應模糊滑模控制律為

u=1b[（a-k）e（t）+aω*r（t）+

d+ω·*r（t）-htanh（s）]。（23）

為取得最小控制，存在參數h^滿足滑模條件以及ε=h^-h*，ε取表1正小數。h^可表示為h^=p^Tw，其中，p^為取得最小滑模控制的最優矢量。

定義參數矢量誤差為

p～=p-p^。（24）

構造Lyapunov函數為

v=12s2+12βp～Tp～。（25）

對其求導得到

v·=ss·+1βp～Tp～·=

s[-bhtanh（s）+f（t）]+1βp～Tp～·≤

-|s|（bh-|f（t）|）+1βp～Tp～·=

-b|s|h*+ε-1b|f（t）|-

b|s|（h-h^）+1βp～Tp·=

-b|s|h*+ε-1b|f（t）|+

1βp～T（p·-βb|s|w）。（26）

考慮到h*為達到滑模條件的最優值，自適應律選為p·=βb|s|w，上式變為v·=-|s|（bh^-|f（t）|）<0，系統漸近穩定。

綜上所述，基于自適應模糊滑模軟切換的永磁同步電機魯棒無源控制系統原理框圖如圖1所示。電流內環通過設計魯棒無源控制器，提高電流預測控制的魯棒性。轉速外環設計自適應模糊滑模軟切換控制器，有效削弱滑模抖振。

圖1基于自適應模糊滑模軟切換的永磁同步?電機魯棒無源控制系統原理框圖

Fig.1Block diagram of robust passive control system ?of PMSM based on adaptive fuzzy sliding ?mode soft switching

3實驗驗證與分析

在永磁同步電機交流調速實驗平臺上，對本文提出的基于自適應模糊滑模軟切換永磁同步電機魯棒無源控制方法進行了相應的驗證，實驗平臺如圖2所示。

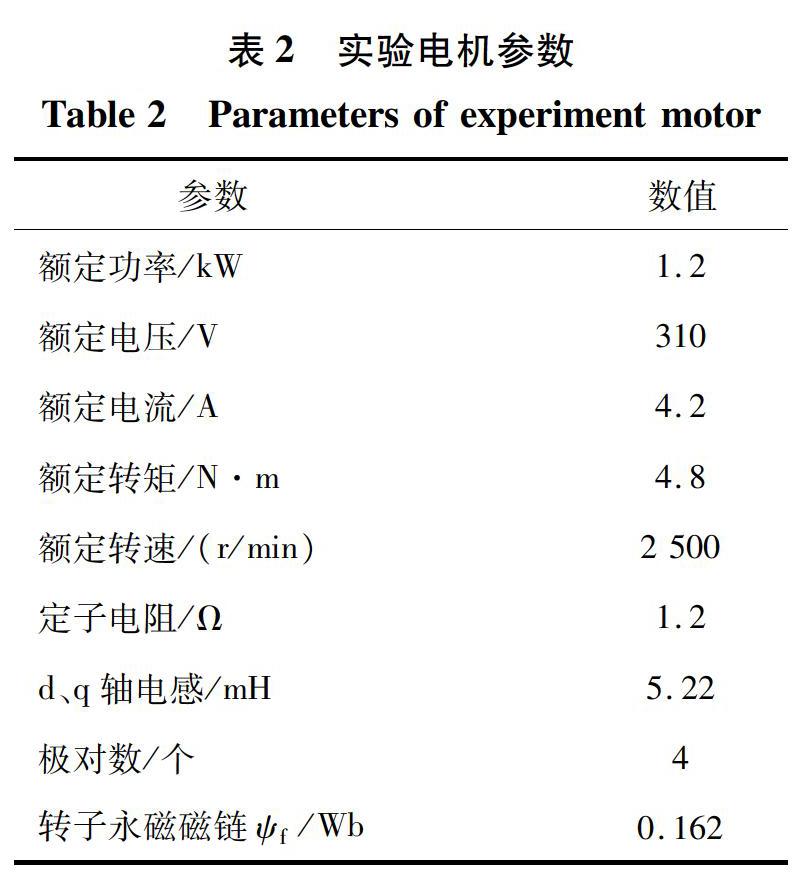
相應地，實驗電機參數如表2所示。

實驗過程選取給定轉速突變、負載擾動以及轉速正弦變化三種典型工況進行實驗研究。另外，為更為直觀地體現新型無源控制方法的優勢所在，該實驗將新型控制方法與傳統滑模控制方法進行對比，并且傳統滑模控制方法轉速外環采用傳統滑模控制，該滑模控制選取補償項ubc=ksgn（s），對比新型軟切換控制;內環電流采用傳統PI控制，對比新型魯棒無源控制。

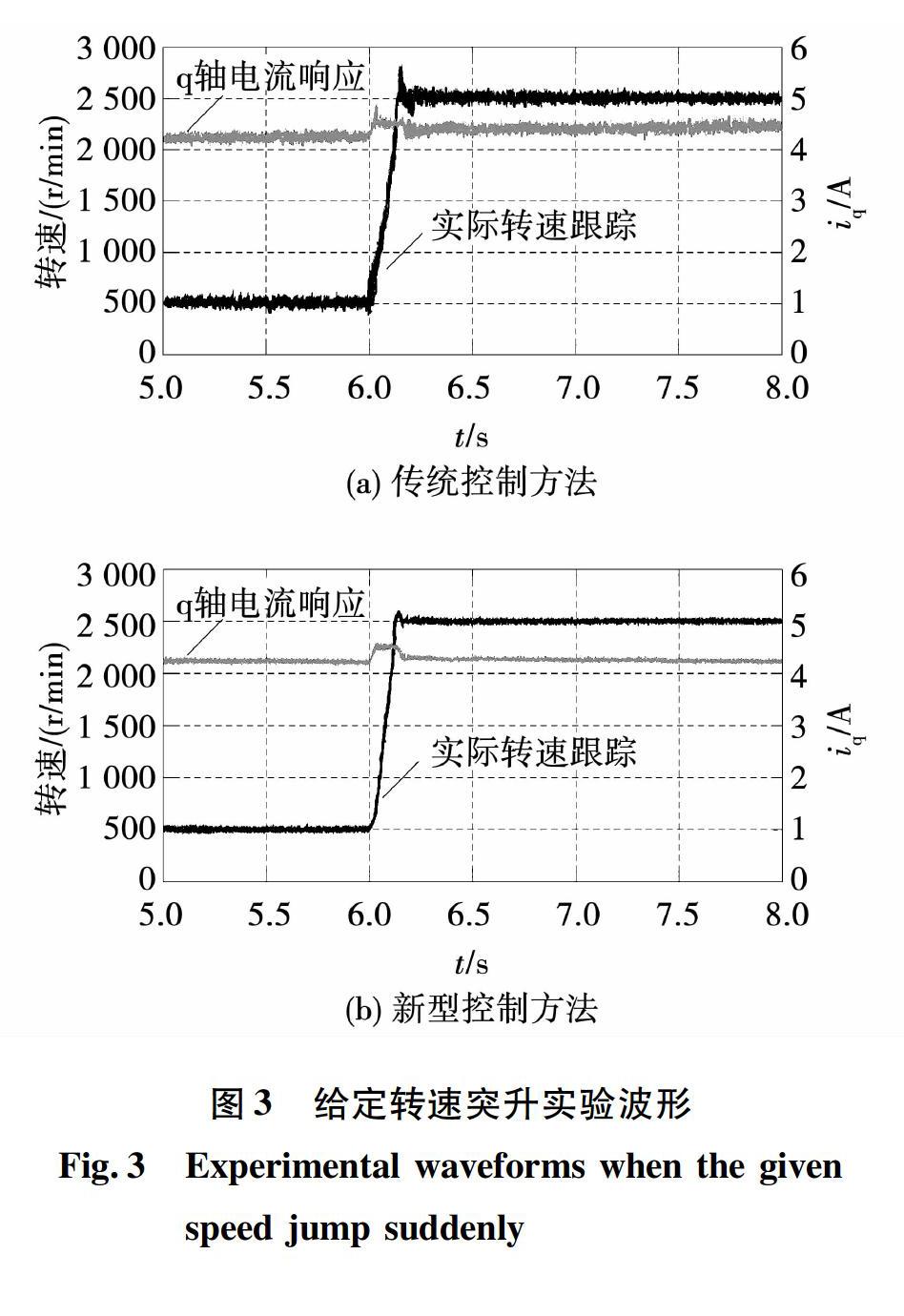
電機運行過程中，考慮給定轉速突變。圖3為電機處于額定負載轉矩、給定轉速突升工況下的實際轉速跟蹤以及q軸電流響應波形，其中圖3（a）為傳統滑模控制對應的響應波形，圖3（b）為新型控制方法對應的響應波形。實驗過程中，電機穩定運行于500 r/min，在6 s時刻，給定轉速由500 r/min突變至額定轉速值，對比圖3（a）和圖3（b），在轉速穩態過程中，傳統控制方法下的電機實際轉速值以及q軸電流值抖振較大，毛刺較為嚴重，而新型控制方法下的電機轉速值和電流值較為平穩，無明顯毛刺，自適應模糊滑模控制的抗抖振優勢得以發揮;在給定轉速突升過程中，圖3（a）傳統控制方法下的實際轉速值存在約250 r/min的超調量，q軸電流值在該過程中上升，同樣存在0.3 A左右的超調量。對比圖3（b）新型控制方法，在給定轉速突升過程中，電機實際轉速上升較為平滑，僅存在約50 r/min的超調量，并且q軸電流值近乎無超調，魯棒無源控制優勢得以發揮。

電機運行過程中，考慮給定負載轉矩的突變。圖4為電機處于額定轉速、突加額定負載轉矩工況下的實際轉速跟蹤以及q軸電流響應波形，其中圖4（a）為傳統滑模控制對應的響應波形，圖4（b）為新型控制方法對應的響應波形。實驗過程中，在6 s時刻之前，電機空載穩定運行于額定轉速值，在6 s時刻，突加額定負載，對比圖4（a）和圖4（b），在負載穩態過程中，空載工況下，傳統控制方法和新型控制方法下的電機實際轉速值以及q軸電流值均較為平穩，抖振較小，突加額定負載后，傳統控制方法下的轉速電流響應波形出現較為嚴重的抖振現象，對比圖4（b）新型控制方法，相應的轉速電流相應波形較給定負載前無明顯變化，體現出新型控制方法對于外部負載擾動的較強魯棒性;在突加負載過程中，兩者q軸電流值均迅速上升至額定值，對比圖4（a）和圖4（b），傳統控制方法下的電流上升存在1 A左右的超調量，同時實際轉速瞬間降低約400 r/min，約0.15 s后趨于穩定。而新型控制方法下的q軸電流僅存在約0.2 A的超調，并且轉速值近瞬間降低100 r/min，后迅速上升至穩態值，動態性能優良。新型控制方法在抗擾動魯棒性方面的優勢得以體現。

為驗證新型控制方法在轉速時變工況下的實際轉速跟蹤響應性能，電機運行過程中，給定轉速正弦波形實時變化，并且考慮給定負載轉矩的突變。圖5給定電機轉速正弦變化下的實際轉速跟蹤響應波形，其中圖5（a）為傳統滑模控制對應的響應波形，圖5（b）為新型控制方法對應的響應波形。實驗過程中，在6.5 s時刻之前，電機處于空載工況，給定電機最大值2 500 r/min，最小值500 r/min的正弦變化轉速值，由圖可以看出，空載工況下，傳統控制方法與新型控制方法實際轉速均可較好地響應給定轉速，新型控制方法在轉速抖振方面占據一定優勢。在6.5 s時刻，突加額定負載，傳統控制方法下的轉速跟蹤立即出現較為嚴重的抖振現象，實際轉速無法準確跟蹤給定。相較于新型控制方法，突加負載后的轉速除在6.5 s時刻瞬間存在較小的轉速下降外，其余時刻轉速跟蹤與空載工況下幾乎相同，抖振現象不明顯，轉速跟蹤響應性能優良，新型控制方法在抗擾動魯棒性方面的優勢得以體現。

4結論

本文提出一種基于自適應模糊滑模軟切換的永磁同步電機魯棒無源控制方法。電流內環通過設計魯棒無源控制器，提高電流預測控制的魯棒性。轉速外環設計模糊滑模軟切換控制器，利用雙曲正切函數代替符號函數，實現軟切換連續控制。采用自適應模糊控制法估計集成不確定邊界，有效削弱滑模抖振。

以一臺1.2 kW永磁同步電機為實驗對象，研究基于本文提出新型控制方法下的轉速電流響應波形，考慮給定轉速和給定負載轉矩突變兩種典型工況對電機運行的影響。實驗過程對比傳統滑模控制方法和新型控制方法，結果表明本文提出的新型控制方法可有效削弱傳統永磁同步電機滑模控制固有的抖振現象，轉速動態響應優良，并且對外部負載擾動有著較強的魯棒性，該新型控制方法在高精度伺服應用領域有著廣闊的前景。

參 考 文 獻：

[1]周荔丹， 李杏， 姚鋼，等. MP?MMC驅動六相永磁風力發電機建模及控制研究.電機與控制學報，2019， 23（5）： 84.

ZHOU Lidan， LI Xing， YAO Gang， et al. Modeling and control for six phase permanent mag?netwind turbine driven by MP?MMC. Electric Machines and Control， 2019， 23（5）： 84.

[2]蓋江濤， 黃守道， 黃慶， 等. 基于負載觀測的永磁電機驅動系統自抗擾控制.電工技術學報， 2016， 31（18）： 29.

GAI Jiangtao，HUANG Shoudao，HUANG Qing，et al.Active?disturbance rejection controller for perma?nent magnet motor drive system control based on load observer. Transactions of China Electro?technical Society， 2016， 31（18）： 29.

[3]彭熙偉， 高瀚林. 永磁同步電機的改進對角遞歸神經網絡PI控制策略.電機與控制學報， 2019， 23（4）： 126.

PENG Xiwei， GAO Hanlin. Improved diagonal rec?ursion neural network and PI control of permanentmagnet synchronous motor. Electric Machines and Control， 2019， 23（4）： 126.

[4]劉春強， 劉伊倫， 孔凡一， 等. 基于時變參數擾動觀測器補償的永磁同步電機非光滑速度調節器.電工技術學報， 2019， 34（4）： 664.

LIU Chunqiang， LIU Yilun， KONG Fanyi， etal. Non?smooth speed controller based on time?varying p?arameter disturbance observer compensation for per?manent magnet synchronous motor. Transactionsof China Electro?technical Society， 2019， 34（4）： 664.

[5]林立， 黃蘇融. 永磁同步電機系統線性化H∞魯棒控制.電機與控制學報， 2009， 13（4）： 541.

LIN Li， HUANG Surong. H∞Robust control with linearization technique for interior permanent magnet synchronous motor servo system. Electric Machines and Control， 2009， 13（4）： 541.

[6]楊書生， 鐘宜生. 永磁同步電機轉速伺服系統魯棒控制器設計.中國電機工程學報， 2009， 29（3）： 84.

YANG Shusheng， ZHONG Yisheng. Robust controller design for PMSM speed servo systems. Proc?eedings of the CSEE， 2009， 29（3）： 84.

[7]高慶忠， 關煥新， 于子淞， 等. 自適應補償器永磁同步電機積分型連續滑模控制.電機與控制學報， 2017， 21（2）： 103.

GAOQingzhong， GUAN Huanxin， YU Zisong， et al. Integral continuous sliding mode control strategy with adaptive compensator for permanent magnet synchronous motor. Electric Machines and Control， 2017， 21（2）： 103.

[8]崔家瑞， 高江峰， 張波， 等. 永磁同步電機滑模變結構魯棒控制.電機與控制學報， 2016， 20（5）： 84.

CUI Jiarui， GAO Jiangfeng， ZHANG bo， et al. Robust control of synchronous motor based on sliding mode variable structure. Electric Machines and Control， 2016， 20（5）： 84.

[9]吳春， 齊蓉， 高峰. 基于擴張PCHD模型的永磁同步電機無源控制. 控制與決策， 2014， 29（5）： 895.

WU Chun， QI Rong， GAO Feng. Passivity?based control of permanent?magnet synchronous motor based on extended PCHD.Control and Decision， 2014， 29（5）： 895.

[10]劉棟良， 崔言飛， 趙曉丹， 等. 基于反推控制的永磁同步電動機速度的模糊控制.電工技術學報， 2014， 29（11）： 38.

LIU Dongliang， CUI Yanfei， ZHAO Xiaodan， et al. Fuzzy control of speed of permanent magnet synchronous motor based on backstepping control. Transactions of China Electrotechnical Society， 2014， 29（11）： 38.

[11]MORAWIEC M. The adaptive backstepping control of permanent magnet synchronous motor supplied by current source inverter. IEEE Transactions on Industrial Informatics， 2013， 9（2）： 1047.

[12]ZHANG X，SUN L，ZHAO K，et al.Nonlinear speed control for PMSM system using sliding?mode control and disturbance compensation techniques. IEEE Transactions on Power Electronics， 2013， 28（3）： 1358.

[13]CHANG S，CHEN P，TING Y，et al.Robust current control?based sliding mode control with simple uncertainties estimation in permanent magnet synchronous motor drive systems. IET Electric PowerApplications， 2010， 4（6）： 441.

[14]LIU X，ZHANG C，LI K.Robust current control based generalized predictive control with sliding mode disturbance compensation for PMSM drives. ISA Transactions， 2017， 71（2）： 542.

[15]BAIK I，KIM K，YOUN M.Robust nonlinear speedcontrol of PM synchronous motor using boundary layer integral sliding mode control technique. IEEE Transactions on Control Systems Technology， 2010，8（1）： 47.

[16]S LI， M ZHOU， X YU.Design and implementation of terminal sliding mode control method for PMSM speed regulation system. IEEE Transactions on Industrial Informatics， 2013， 9（4）： 1879.

[17]ZHANG B，PI Y，LUO Y.Fractional order sliding?mode control based on parameters auto?tuning for velocity control of permanent magnet synchronous motor. ISA Transactions， 2012， 51（5）： 649.