簡單枚舉法在小學數學問題解決中的應用

浙江省義烏市經濟開發區學校 王菊華

數學思想方法是數學的靈魂和精髓，是對數學事實與理論經過概括后產生的本質認識，也是解決問題的基本策略。如果說抽象與建模這些數學思想在教學中如“潤物細無聲”一樣滲透在每個教學環節，而枚舉法的數學思想，則可以在教學中大張旗鼓的與學生進行互動與交流。枚舉法是一種很重要的數學思考方法，在很多問題的思考過程中，都能發揮很重要的作用。

枚舉法是將問題所涉及的所有情況全部羅列出來，一一加以討論，從而解決問題的一種方法。當問題出現的情況是有限種，而且這些情況又無法統一處理時，就可以用枚舉法來解決。這種方法，就是先將題目中的答案，分成幾種不同的類型，然后將每一類中各種不同的情況一一列舉出來，不重復，不遺漏，最后計算總數的方法。運用枚舉法解題的關鍵是有序思考，正確分類，分類不全就會造成遺漏，分類不清，使第一類中有第二類，第二類中有第三類，互相包涵，那么就會重復，這樣結果也就很難正確了。為此必須注意兩點：一分類時要全，不能有遺漏；二枚舉時要全，要將符合要求的每一個對象都列舉出來。在枚舉時，我們可以采用列算式，列表格，寫序號，畫樹狀圖等形式來呈現。下面我們一起來看看枚舉法在小學數學問題解決中的一些特例。

一、列算式枚舉

無論是低段，還是中高段，在平時教學中，我們經常會不經意地使用枚舉法。例如，學習二年級怎樣取錢時，往往引導學生有序思考，一一枚舉，采用列算式的形式呈現。

例1：小紅有若干張紙幣，8張1元，4張2元，,1張5元，他要拼出8元錢來，有幾種不同的拼法？

分析：怎樣才能有序地進行思考，我們可以根據紙幣的大小，按從大到小分類排列。比如8元錢，可以1張5元+1張2元+1張1元，但這樣書寫太麻煩，我們往往直接采用算式來表示。

8=5+2+1 8=2+2+1+1+1+1

8=5+1+1+1 8=2+1+1+1+1+1+1

8=2+2+2+2 8=1+1+1+1+1+1+1+1

8=2+2+2+1+1

例2：將23分成三個不同的奇數之和，共有幾種不同的分法？

分析：按奇數從小到大分類排列，有序思考。

1+3+19=23 3+5+15=23

1+5+17=23 3+7+13=23

1+7+15=23 3+9+11=23

1+9+13=23 5+7+11=23

一共有8種不同的分法。

二、列表格枚舉

我們采取枚舉法來解決問題，碰到數據較多時，就會列成表格來枚舉。因為使用表格不僅可以對數據進行排序，而且可以清楚地看出數據的變化，從而快速地解決問題，如，三年級的租車問題，長方形等周等積問題，五年級的雞兔同籠問題等，都可以采用列表格枚舉解決。

例1：用26根1厘米長的小棒圍成一個長方形，有多少種不同的圍法？你發現了什么？怎樣圍面積最大？

分析：這是典型的三年級的長方形等周問題。26厘米是長方形的周長，可以先求出長+寬=26÷2=13(厘米)，列表格枚舉如下：

長/厘米 12 11 10 9 8 7寬/厘米 1 2 3 4 5 6面積/平方厘米 12 22 30 36 40 42

觀察發現：周長一定時，長和寬越接近，面積越大。

一共有6種不同的圍法，當長等于7米，寬等于6米時，面積最大。

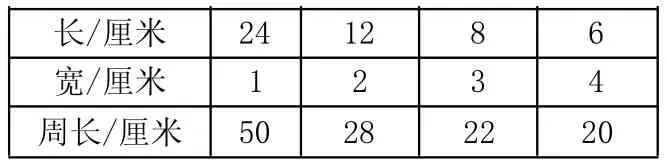
例2：用24個邊長是1厘米的正方形，可以拼成多少種不同的長方形？你發現了什么？

分析：這是典型的三年級的長方形等積問題。18平方厘米是長方形的面積，可以先求出24=24×1=12×2=8×3=6×4，列表格枚舉如下：

長/厘米 12 11 10 9 8 7寬/厘米 1 2 3 4 5 6面積/平方厘米 12 22 30 36 40 42

觀察發現：面積一定時，長和寬越接近，周長越小。

一共有4種不同的圍法，當長等于7米，寬等于4米時，周長最小。

長/厘米 24 12 8 6寬/厘米 1 2 3 4周長/厘米 50 28 22 20

例3：雞兔同籠，一共有28只腳，9個頭，請問雞兔各有幾只？可以用枚舉法，是最基本的方法，把所有可能出現的情況都羅列出來。

雞 0 1 2 3 4 5 6 7 8 9兔 9 8 7 6 5 4 3 2 1 0腳 36 34 32 30 28

枚舉法并不“笨”，相反，對小學生來說枚舉法更容易理解記憶。

例4：有12個人植樹，男生種3棵，女生種2棵，一共種了27棵，男女生各有幾人？

分析：此題也可看成雞兔同籠問題，但三年級學生列算式解決并不容易，若把所有可能出現的男女生人數情況都一一羅列成表，再計算出樹的棵數，依次是24,25,26,27，……，就可以輕而易舉地找到我們所需要的答案。那就是男生3人，女生9人。

男 0 1 2 3 4 5 6 7 8 9 10 11 12女 12 11 10 9 8 7 6 5 4 3 2 1 0樹 24 25 26 27

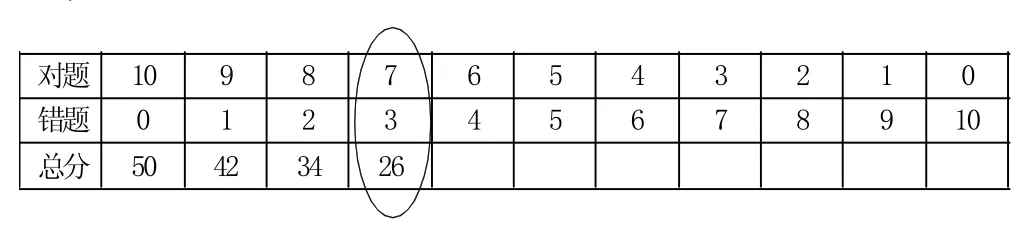
例5：一次數學競賽共有10道題，做對一道得5分，做錯一道倒扣3分。小周考了26分，他做對了幾道題？

分析：此題跟雞兔同籠問題非常類似，一共有13種情況，做對最多12道，最少0道。把所有可能出現的情況一一羅列成下表：

對題 10 9 8 7 6 5 4 3 2 1 0錯題 0 1 2 3 4 5 6 7 8 9 10總分 50 42 34 26

再計算出對應的總分，依次是50,42,34,26，……，我們可以輕而易舉地找到我們所需要的答案。那就是做對7道，做錯3道。

此題可以用方程解，但用方程解對部分同學有一定的難度。用假設法列算式，對一題和錯一題相差8分，學生理解也會更困難，很容易做錯，如果用枚舉法，就可以避免以上困惑。枚舉時只要找到自己所需要的答案，后面可以不用再繼續算下去。

三、寫序號分類枚舉

寫序號分類枚舉，就像字典排列法，在枚舉時，像字典里的單詞順序那樣排列出所有答案，每個位置都按從小到大排列，適用于二三年級經常遇到的一些組數問題。怎樣才能做到不遺漏，不重復，關鍵在于分類，我們可以根據題目要求按同一數位上的不同數字進行分類。

例1:用0，2，4，7四個數字，可以組成多少個沒有重復數字的三位數？

分析：0不能放在最高位，但可以放在十位和個位，可以按百位上的數字2，4，7進行分類。

①百位上是 2 的三位數：204，240，207，270，247，274；

②百位上是 4 的三位數：402，420，407，470，427，472；

③百位上是 7 的三位數：702，720，704，740，724，742；

一共有 6×3=18（個）

例2：一本書共100頁，在排頁碼時要用多少個數字是6的鉛字？

把它分成兩類來考慮。

①個位是 6 的數字有:6，16，26，36，46，56，66，76，86，96，共10個。

②十位是 6 的數字有:60，61，62，63，64，65，66，67，68，69，共10個。

10+10=20（個）答：在排頁碼時，要用20個數字是6的鉛字。

例3：個位是6，且能被3整除的三位數有多少個？

分析：個位是6，組數要符合被能3整除，只要考慮百位和十位之和是3的倍數就可以了。按百位是1，2，3，4，……，9有序思考，共寫出了以下9組數。

①126，1 56，186； ⑥606，636，666，696；

②216，246，396； ⑦726，756，786；

③306，336，366，396； ⑧816，846，876；

④426，456，486； ⑨906，936，966，996；

⑤516，546，576；

3×6+4×3=30（個） 答：共30個。

例4：一個三位數的各個數位之和為10，且各個數位上的數字各不相同，這樣的三位數共有幾個？

分析：可以按三個數之和等于10，寫出三個數里含有1，含有2，含有3，含有4，……的所有算式進行分類，再有序思考，再組成三位數。

①含有 1:1+0+9=10 109，1 90，901，910；

1+2+7=10 127，172，217，271，712，721；

1+3+6=10 136，163，316，361，613，631；

1+4+5=10 145，154，415，451，514，541；

②含有 2：2+0+8=10 208，280，802，820；

2+3+5=10 235，253，325，352，523，532；

③含有 3：3+0+7=10 307，370，703，730；

④含有 4：4+0+6=10 406，460，604，640。

符合條件的共有：4×4+6×4=40（個）

由于分類標準不一樣，思考方法也會隨之改變。

例 5：淘氣從 1 開始寫連續的自然數：1，2，3，4，5，……，當寫完某個自然數的時候停止，發現一共寫了30個數字“1”。那么他寫的最后一個數自然數是幾？

解：按數的區間分：

①1～9 之間：只有 1，有 1 個“1”；

②10～19之間：含有1的數共有11個“1”；

③20～99之間：含有1的數共有8個“1”；

④ 前三步已有 1+11+8=20個“1”，還有 10個“1”，接下來100～108，共有 10 個“1”。所以，“1～108”之間，一共有 30 個“1”，最后一個自然數為108。

按數位分：

解：①1～99 之間：數個位上的 1，從 1，11，21，……，91，共有 10 個“1”；

②1～99之間：數十位上的 1，從 10，11,12，……,19，共有10 個“1”；

③已有 10+10=20個“1”，還有 10個“1”，接下來 100～108，數百位上的 1，共有 9 個“1”。加上 101 個位上的“1”，共有10 個“1”，所以，“1～108”之間，一共有 30 個“1”，最后一個自然數為108。

四、畫樹狀圖枚舉

例1：小明有10塊糖，每天至少吃3塊，吃完為止，那么共有幾種不同的吃法？

分析：首先要注意每天至少吃3塊糖，解決這個問題，也可用樹狀圖表示。

注：算式中的加數表示各天吃的顆數，例如3+7表示第一天吃3顆，第二天吃7顆，7+3表示第一天吃7顆，第二天吃3顆。

例2：用一臺天平。和1克3克，9克的砝碼各一個。規定砝碼只能放在天平的右邊。用這三個砝碼能稱出幾種不同的重量。

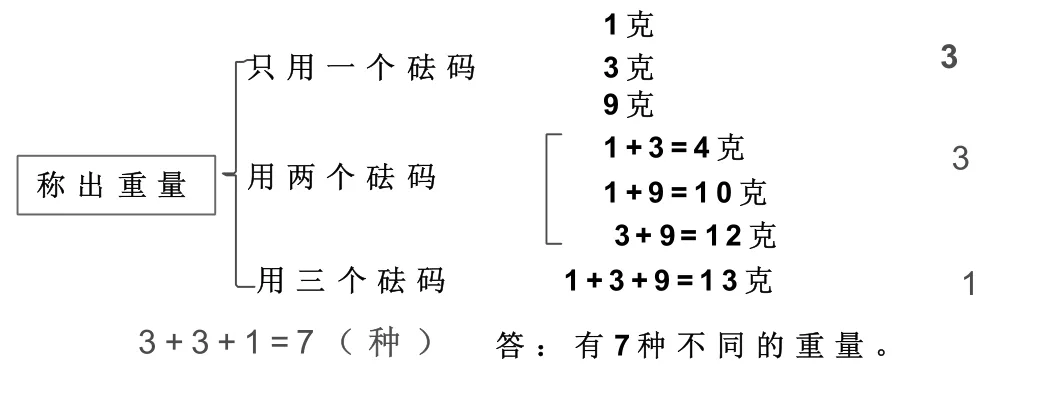
枚舉法雖然看起來有點笨拙，但卻是很多數學知識探究、問題解決的最有效的方法之一。同時，列算式枚舉、列表格枚舉、寫序號分類枚舉、畫樹狀圖枚舉還承載了數學語言描述簡潔，解決問題有序思考、抽象思維、數形結合等思想方法的滲透教學。枚舉法比較好理解，有利于中下等學生學習，還能解決用算式或方程小學生沒法解決的問題，起到化難為易的作用。良好的數學思想和方法，會讓學生終身受益，讓我們不斷探索能使學生養成優秀思維品質的數學思想和方法，在路上，從容行走，優雅為師，做一個讓學生敬佩并會念想的老師！