AR模型中AO類異常值探測及其在GPS衛星鐘差預報中的應用

韓松輝，張國超，張 寧，朱建青

1. 信息工程大學基礎部，河南 鄭州 450001； 2. 中國人民解放軍78092部隊，四川 成都 610000； 3. 蘇州科技大學理學院，江蘇 蘇州 215009

時間序列分析是處理測繪導航數據的常用技術之一，比如使用時間序列模型對衛星鐘差數據進行處理就具有明顯的優勢[1-2]。但是，衛星鐘差的歷史觀測序列中可能包含AO類異常值(只對出現異常值歷元的觀測值產生影響，不影響其他歷元的觀測值)[3-4]，這嚴重影響了時間序列模型識別和參數估計的精度。目前已有一些學者對時間序列中異常值的探測問題進行了研究，并提出了許多解決方法，如中位數法[5]、抗差估計法[3,6]、Allan方差法[7-8]和抗差自適應濾波法[9]等。但已有的方法均存在一定的不足之處，如對異常值的定位存在偏差，無法有效地對異常擾動進行估計等[10]。異常值探測是時間序列分析中的一個重要環節[11-15]，如何基于時間序列模型，對序列中的AO類異常值進行探測正逐漸被學者所關注。文獻[16]使用時間序列中的AR模型、Bayes統計理論對序列中的異常值進行探測，進而修正了相應的AR模型。文獻[17—18]采用平穩時間序列的χ2檢測法檢測衛星鐘運行中的異常情況。文獻[19]利用Bayes理論在AR模型中引入識別變量，通過比較這些識別變量的后驗概率值與事先給定的閾值來進行異常值探測。上述基于時間序列的算法對于序列中的異常值探測均有一定的參考意義，但是以上幾種算法有的未對異常擾動進行估計，有的需要經過復雜的抽樣過程，有的需要計算后驗概率。

時間序列中異常值探測的相關計算比較復雜，可以采用基于極大似然函數的EM算法(expectation maximization algorithm)[20]進行處理。極大似然函數包含了每一個觀測值的信息，使用極大似然函數對觀測序列中的異常值進行探測是很好的選擇。EM算法已經被廣泛應用于處理缺損數據、截尾數據、成群數據、帶有討厭參數的數據以及對異常擾動視同缺失進行再補充的不完全數據等[21-26]。EM算法是一種簡單穩定的迭代算法，每一次迭代都能保證似然函數值增加，并最終收斂到一個局部極大值。已經有多位學者使用EM算法對時間序列問題進行了研究，部分成果已經成功用于解決實際問題，比如，EM算法應用于線性時間序列參數估計與預測、非線性時間序列參數估計、整值時間序列參數估計以及回歸混合模型參數估計等[27-31]。目前，也有學者討論了基于EM算法的異常擾動處理問題，比如，t型估計中異常擾動的處理問題[32-33]，非高斯噪聲線性回歸模型中異常擾動的處理問題[34]，均值漂移模型和方差膨脹模型中異常擾動的處理問題[35]。但是，目前極少有學者討論基于EM算法的時間序列異常值探測問題。文獻[31]提出了采用EM算法估計MPT(1)模型參數的算法，雖然文中分析了該算法對異常值的抗干擾能力，但是并沒有進一步提出異常值的探測方法。

本文將EM算法應用于AR模型觀測序列AO類異常值的探測與修復之中。首先，基于AR模型，給出引入識別變量的AO類異常值探測模型。然后，利用EM算法推導AR模型中AO類異常值的定位與異常擾動估值的迭代公式，提出一種AR模型中AO類異常值探測算法。該算法通過簡單迭代計算出AR模型系數、異常值的位置和異常擾動的估值。最后，為了驗證本文算法的有效性，分別給出仿真算例和實測GPS衛星鐘差算例，并分別對單個AO類異常值和成片AO類異常值進行探測。分析發現本文算法對單個AO類異常值和成片AO類異常值均可精確探測，并且在探測成片AO類異常值時，未出現掩蓋和淹沒現象。

1 異常值探測模型和EM算法

1.1 異常值探測模型

設時間序列數據{yt}符合AR(p)模型，則有

(1)

基于識別變量標記異常值方法，可以建立基于AR模型的AO類異常值探測模型[10,19]

(2)

式中，{xt}為觀測得到的可能包含AO類異常值的時間序列；{yt}為無法觀測的正常序列；δt為AO類異常值的識別變量，并且δt服從兩點分布，取值為0或1，如果δt=1，則xt包含AO類異常值，相應AO類異常值的異常擾動大小為wt，如果δt=0，則xt不包含AO類異常值。在上述構造的AO類異常值探測模型中，增加了探測異常值的參數δt、wt，基于此模型探測異常值時，如何正確估計模型中的未知參數是首要問題。當觀測數據含有異常值時，應利用數據中包含的一切有用信息來消除異常值的影響。極大似然函數包含了每一個觀測值所提供的信息，可采用極大似然函數進行異常值探測。但是，由于極大似然函數比較復雜，此時面臨模型系數如何計算、異常值位置如何判定、異常值擾動如何估計等問題。為此，本文引入求解極大似然函數方程的EM算法來解決相關計算問題，進而確定模型參數、異常值位置和異常擾動的大小，從而準確擬合出時間序列模型，并獲得精確的異常值探測結果。

1.2 EM算法

EM算法也稱為期望最大化算法，是一種求參數的極大似然估計的方法，可以從非完整數據集中對參數進行極大似然估計[20]。在統計學中，EM算法是在概率模型中尋找參數最大似然估計或者最大后驗估計的算法，其中概率模型依賴于無法觀測的隱藏變量。本文構造的異常值探測模型(2)中，增加的異常值識別變量δt可看成無法觀測的隱藏變量，因此基于AR(p)的異常值探測模型(2)可以采用EM算法進行求解。

令

首先初始化分布參數θ，則由θi計算θi+1的過程由下面兩步組成：

第1步：利用概率模型參數的現有估計值，計算隱藏變量的期望，即對給定的θi，利用對數似然函數lnL計算Q(θ|θi)=Eδt[lnL|X,θi]；

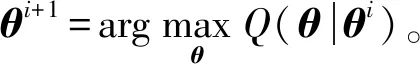
按以上兩步循環迭代，直至收斂，進而獲得參數θ的估計值。在寬松的初始條件下，由EM算法產生的迭代序列{θi}將收斂到似然函數的極值點[36]。

2 基于EM算法的AO類異常值探測方法

由模型(2)可知，xt的概率密度函數為

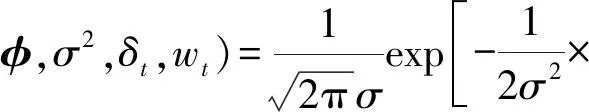
(3)

似然函數為

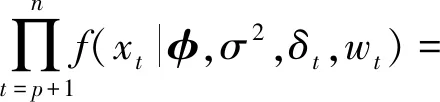
(4)

其對數似然函數為

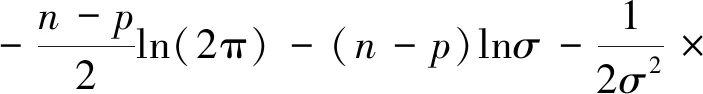
(5)

異常值識別變量δt是無法觀測的隱藏變量，可采用EM算法進行求解。

2.1 計算隱藏變量的期望

令zt=xt-φ1yt-1-…-φpyt-p，則

Q(θ|θi)=Eδt[lnL|X,θi]=

(6)

式中

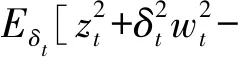
2δtwtzt|θi)]

(7)

已知δt服從0～1分布，令

(8)

此時

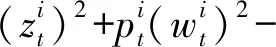
(9)

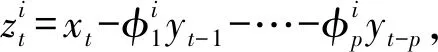
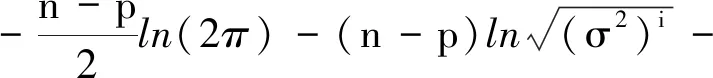
(10)

2.2 模型參數的最大似然估計

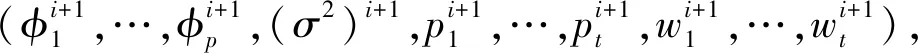
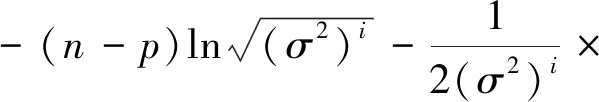
(11)

達到最大。為方便符號表示，在下面的推導過程中省略Q(δ)中的上標i。將Q(δ)分別關于φ1、φ2、…、φp,求導并令其等于零，可得

(12)

將上式整理成矩陣形式為

(13)

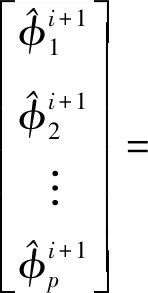
(14)

同理，將Q(δ)分別關于wt、σ2求導并令其等于零，可得

(15)

(16)

該算法不但可以消除異常值的影響而且可以同時得到準確的AR模型。在以上算法中，模型系數、異常值識別變量和異常擾動大小表達式均為嚴格推導所得的結果，具有理論上的嚴密性。算法既利用了原始觀測數據，又同步使用了修正異常擾動后的觀測數據對異常值進行探測，使得計算結果既不偏離原始數據又可消除異常值的影響。另外，算法的所有估計結果均是在一個迭代循環過程中獲得的，估計值之間具有較好的相容性，不會額外引入不同迭代過程之間的計算誤差。

2.3 AO類異常值探測流程

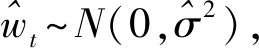
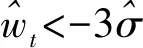
(17)

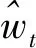
重復第1步(計算隱藏變量的期望)與第2步(模型參數的最大似然估計)，迭代收斂后即可得參數最終解。具體的程序流程如圖1所示。

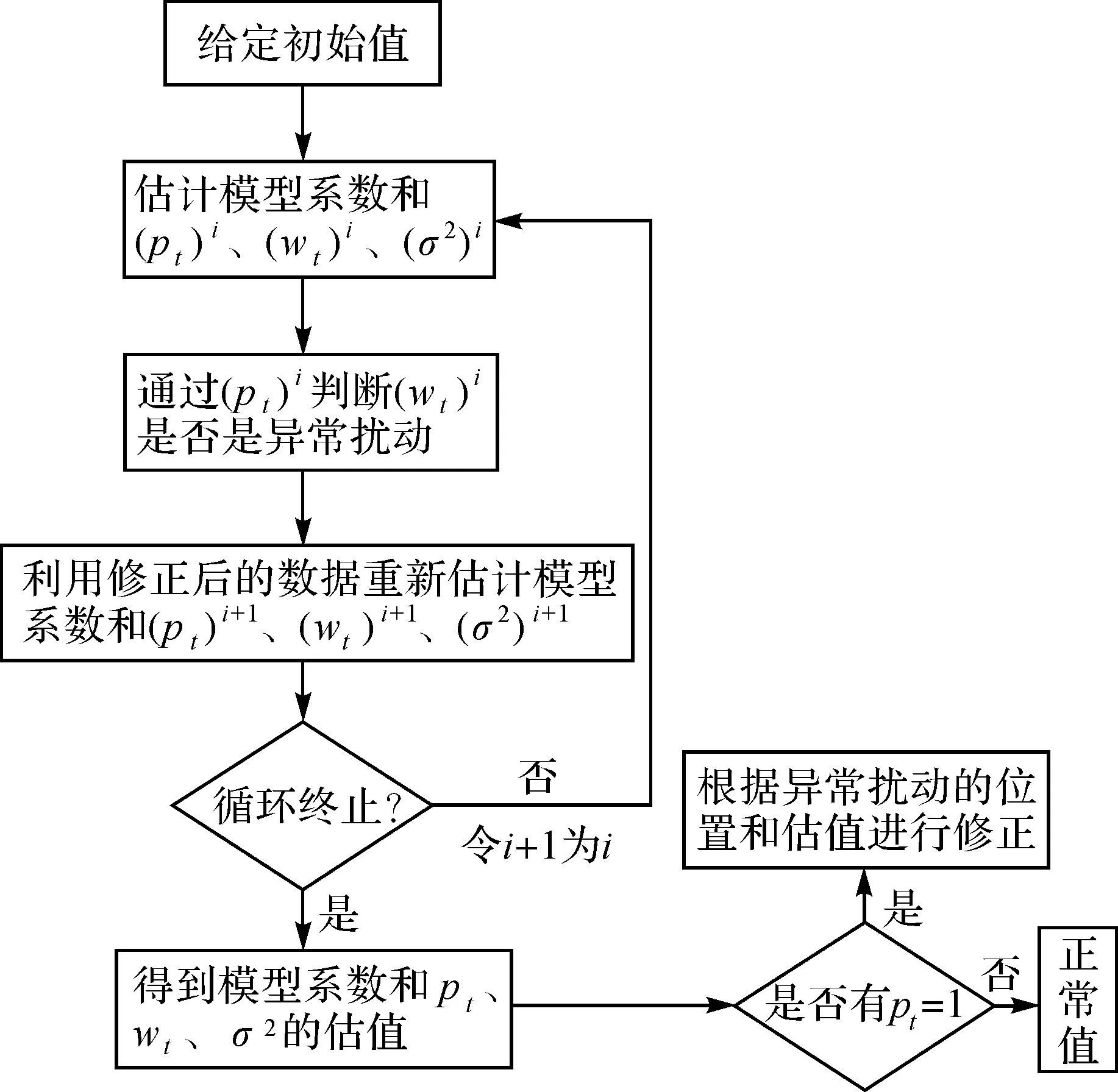
圖1 基于EM算法的AR模型異常值探測與估計流程Fig.1 Flowchart of outliers detection and estimation in AR model based on EM algorithm

3 算例與分析

為驗證本文方法的有效性，給出一個仿真算例和一個衛星鐘差預報算例。

3.1 仿真算例

使用AR(2)模型

生成50個模擬觀測值，并在第20個和第30個觀測值分別添加數值為10和7的AO類異常擾動。使用本文算法對異常值進行探測，并采用常用的3σ原則，所得模型識別變量pt與異常擾動估計wt的結果如圖2、圖3所示。其中，圖3中的星號是真實的AO類異常擾動大小。在后續計算分析中，均采用星號表示真實異常擾動的大小。

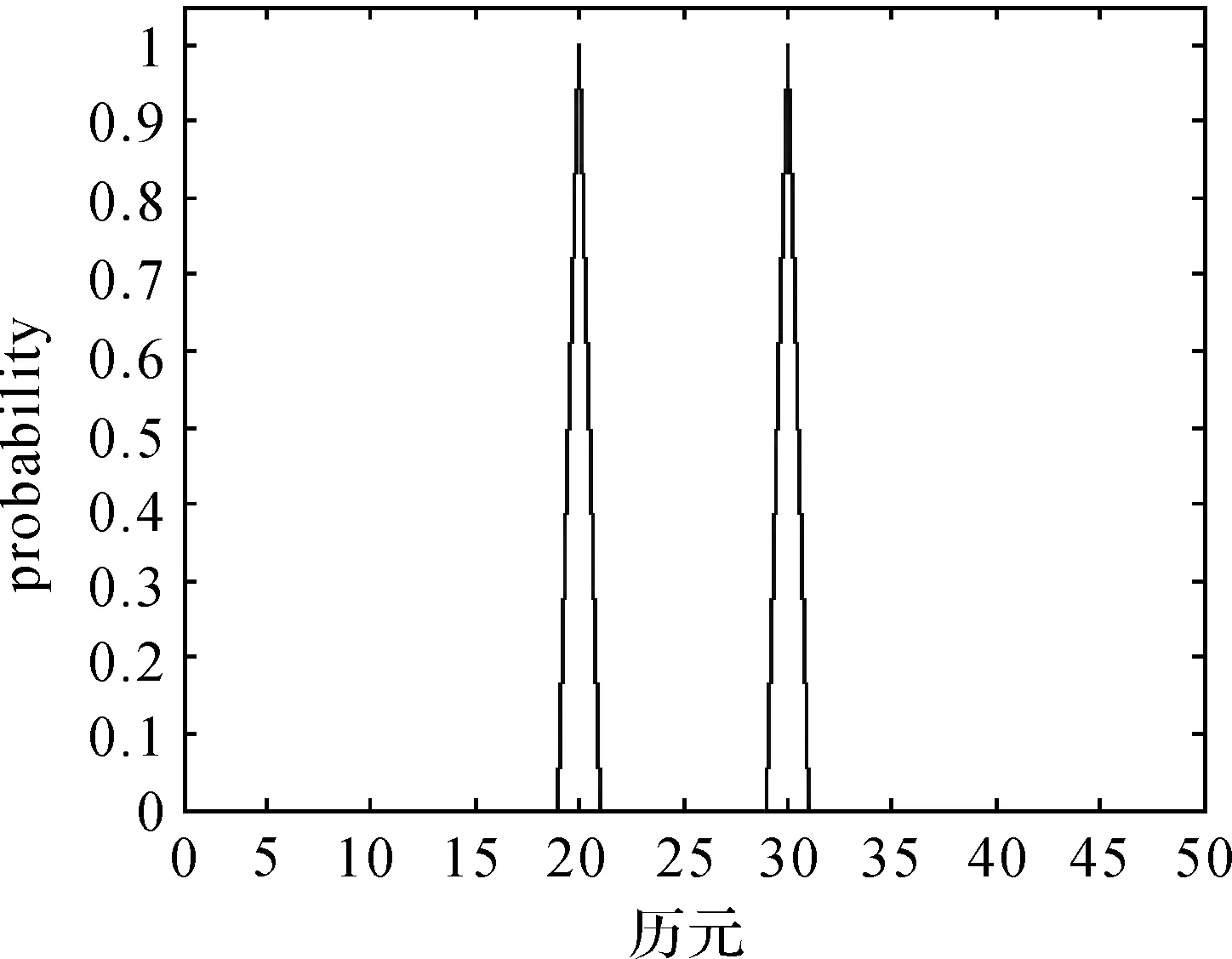
圖2 仿真數據中單個異常擾動的pt結果Fig.2 ptof single outlier in simulation data

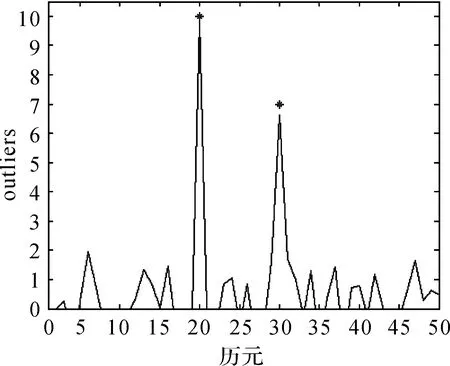
圖3 仿真數據中單個異常擾動的wt結果Fig.3 wt of single outlier in simulation data

分析發現，本文方法可以精確確定AO類異常值的位置，并準確估計異常擾動的大小，所得異常擾動的估計值分別為9.89和6.63。

為檢驗本文方法對成片AO類異常值的探測效果，在第20—24個觀測值上分別加上大小為10的AO類異常擾動，并使用本文提出的算法進行異常值探測，其中pt和wt的計算結果如圖4、圖5所示。

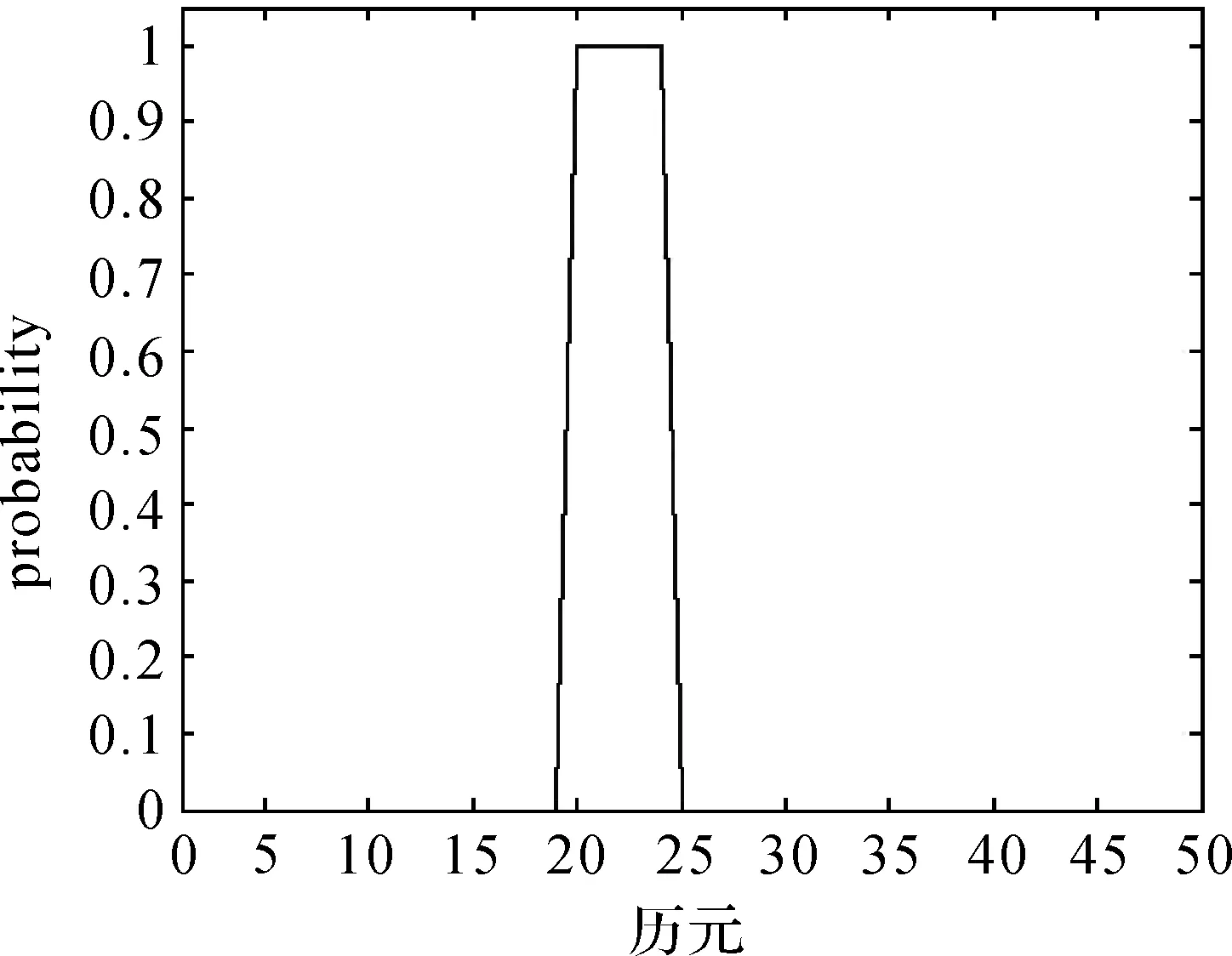
圖4 仿真數據中成片異常擾動的pt結果Fig.4 pt of patches of outliers in simulation data

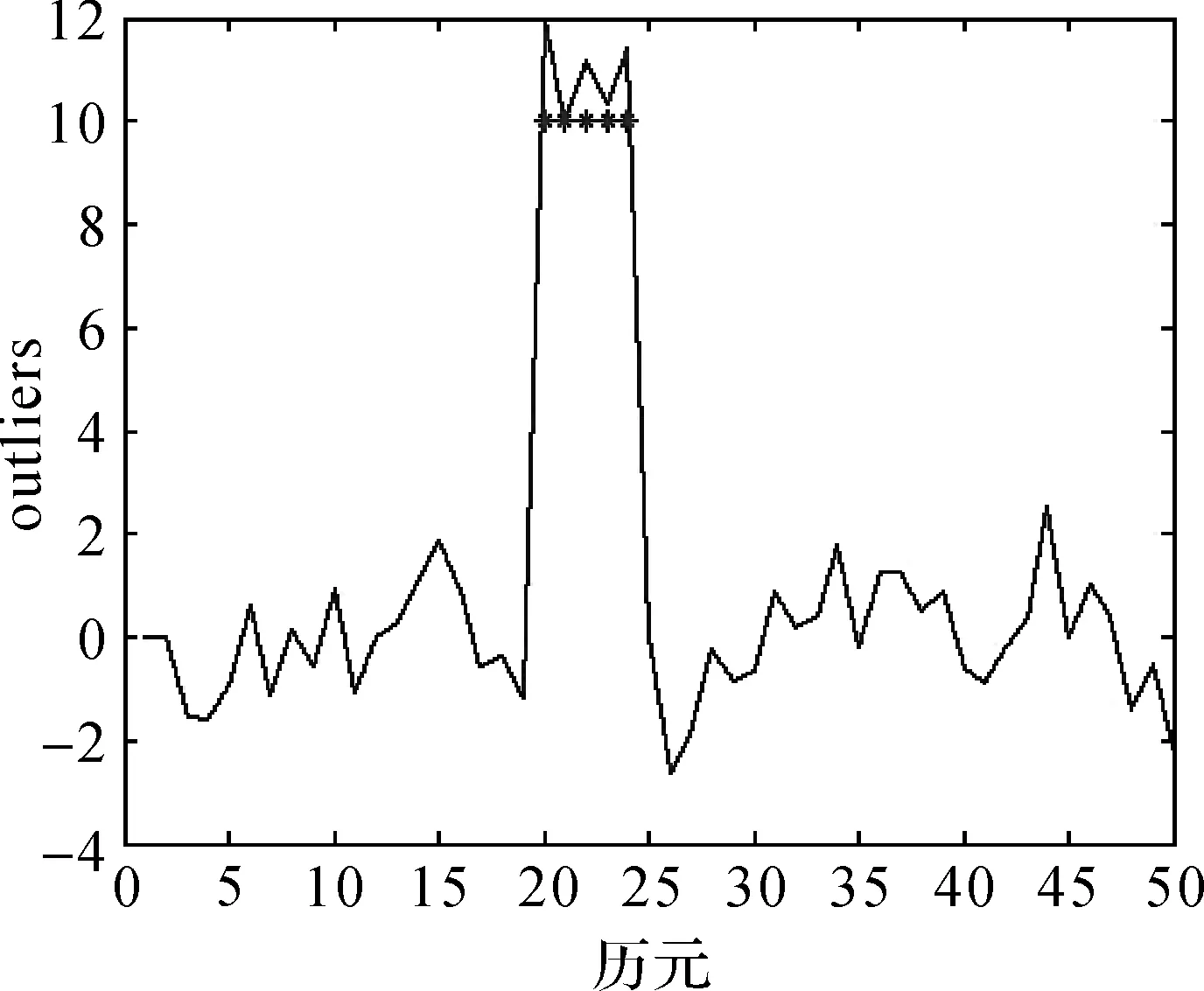
圖5 仿真數據中成片異常擾動的wt結果Fig.5 wt of patches of outliers in simulation data

分析發現，本文方法對成片AO類異常值的定位非常準確，對相應異常擾動大小的估計精度較好，所得異常擾動的估計分別為：11.96、9.95、11.19、10.34、11.40。由計算結果可以看出，本文方法可以對成片AO類異常值進行準確探測，并且沒有出現掩蓋和淹沒現象。

為了對異常值的數量比例、探測成功率、估計精度等進行統計分析，首先盡可能多地增加成片異常值中AO類異常值(大小為10)的個數。發現在總觀測個數是50的情況下，該算法可以準確探測出第14—32位置上的19個AO類異常值，并且異常擾動大小的估計精度也較好。其估計結果分別為：11.09、12.17、11.51、9.91、9.66、8.74、11.62、9.82、11.14、10.33、11.39、10.03、9.03、8.10、9.25、8.88、9.02、10.59、10.29。

其次，分析第20—24個觀測值包含的AO類異常值大小不同的情況。依次加上異常擾動大小為3到9的AO類異常擾動。計算發現，除異常擾動大小為3的情況外，其余情況均可準確探測出異常值位置，并可較準確地估計異常擾動大小，其異常擾動大小的估計值如表1所示。

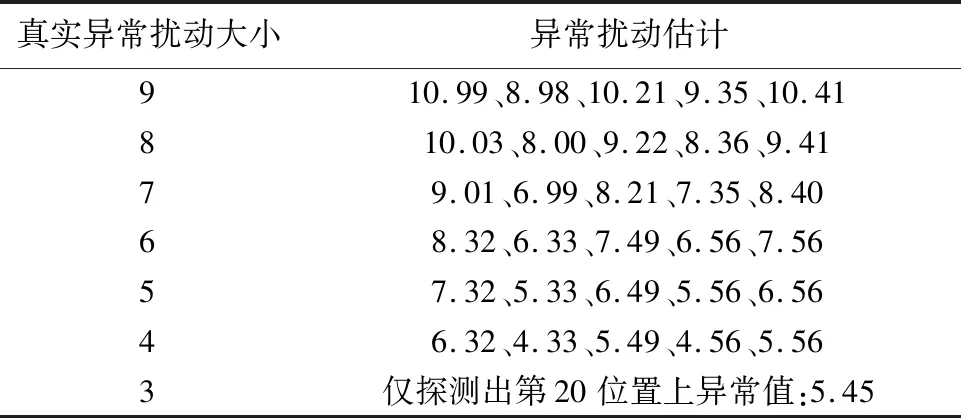
表1 不同大小異常值的估計值

由表1可以發現，當異常擾動越大時異常擾動大小的估計精度越高。當異常擾動大小為3時之所以無法準確探測異常值位置，是因為此時的異常擾動大小與正常的觀測值非常接近(不含異常值時，觀測序列的最大觀測值為2.58)，此時本算法探測效果不好。

接下來，分別在第20個觀測值、第20—21個觀測值、第20—22個觀測值、第20—23個觀測值、第20—24個觀測值加上大小為10的異常值，在每次計算時均生成50個新的模擬觀測值并分別計算10 000次，其成功探測異常值位置的計算結果如表2所示。

表2 采用3σ原則時異常值位置探測的成功率

Tab.2 The frequency which the location of outliers was correctly detected when 3σwas used

異常值位置2020—2120—2220—2320—24成功率/(%)89.1284.1077.4469.5361.84

由表2可以看出，隨著成片AO類異常值中異常值個數的增加，異常值探測成功率是逐漸降低的。分析異常值探測失敗的情況，發現3σ作為閾值偏小，有些不是異常值的情況被誤判為異常值。因此采用4σ原則，在每次計算時均生成50個新的模擬觀測值并分別計算10 000次，其成功探測異常值位置的計算結果如表3所示。

表3 采用4σ原則時異常值位置探測的成功率

Tab.3 The frequency which the location of outliers was correctly detected when 4σwas used

異常值位置2020—2120—2220—2320—24成功率/(%)99.9795.1191.3286.4782.12

由表2和表3可以看出，異常值的探測效果受σ倍數k的影響，雖然采用3σ作為閾值也可以得到較好的異常值探測效果，但是采用4σ原則時異常值探測成功率明顯上升。如何找到最恰當閾值是一個需要繼續研究的問題。對此，文獻[37]認為：在時間序列異常值的探測過程中，閾值過大或過小均不利于異常值探測，在實際中可以設定幾個不同的閾值以便發現數據的結構變化。

3.2 實測算例

隨著衛星導航定位技術的發展，高精度的鐘差預報技術顯得至關重要。一般的，對衛星鐘差進行預報需要建立準確的鐘差預報模型。時間序列模型可以充分考慮到衛星鐘差的趨勢性、周期性和隨機性等特點，因此，使用時間序列模型對衛星鐘差數據進行處理具有明顯的優勢。由于傳播路徑和觀測環境的影響，鐘差的歷史觀測序列可能包含異常值，這嚴重影響了衛星鐘差預報的精度。

在IGS官網發布的GPS衛星精密鐘差數據中提取為期1 d的G16衛星的鐘差數據(單位為秒)，時間為2016年01月01日，數據采樣間隔為5 min，共包括288個歷元。經過兩次差分后序列變為不含趨勢項的平穩序列，其自相關函數和偏自相關函數的計算結果分別如圖6和圖7所示。

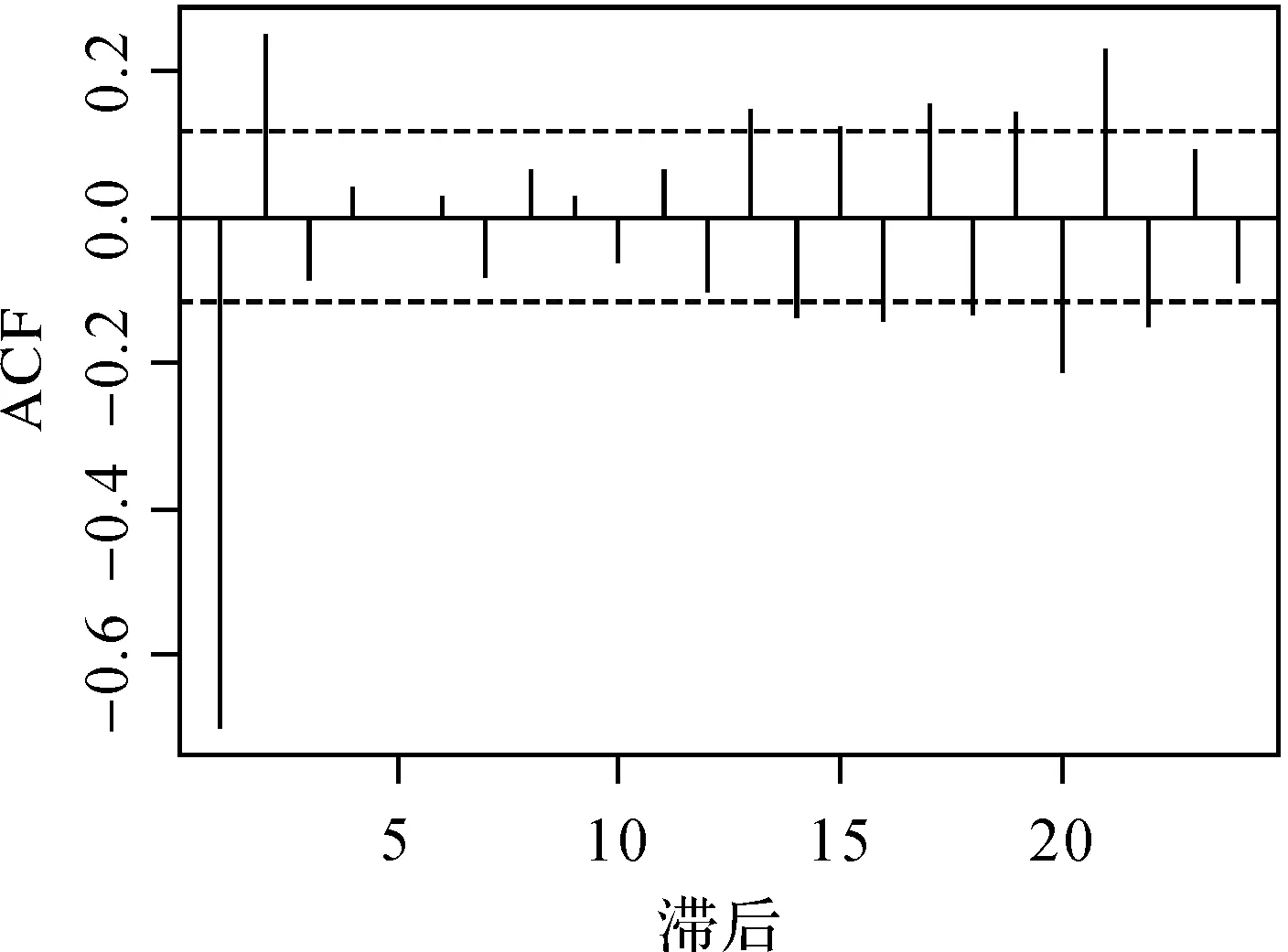
圖6 二次差分鐘差數據的自相關函數圖Fig.6 Sample ACF of two differences clock errors data

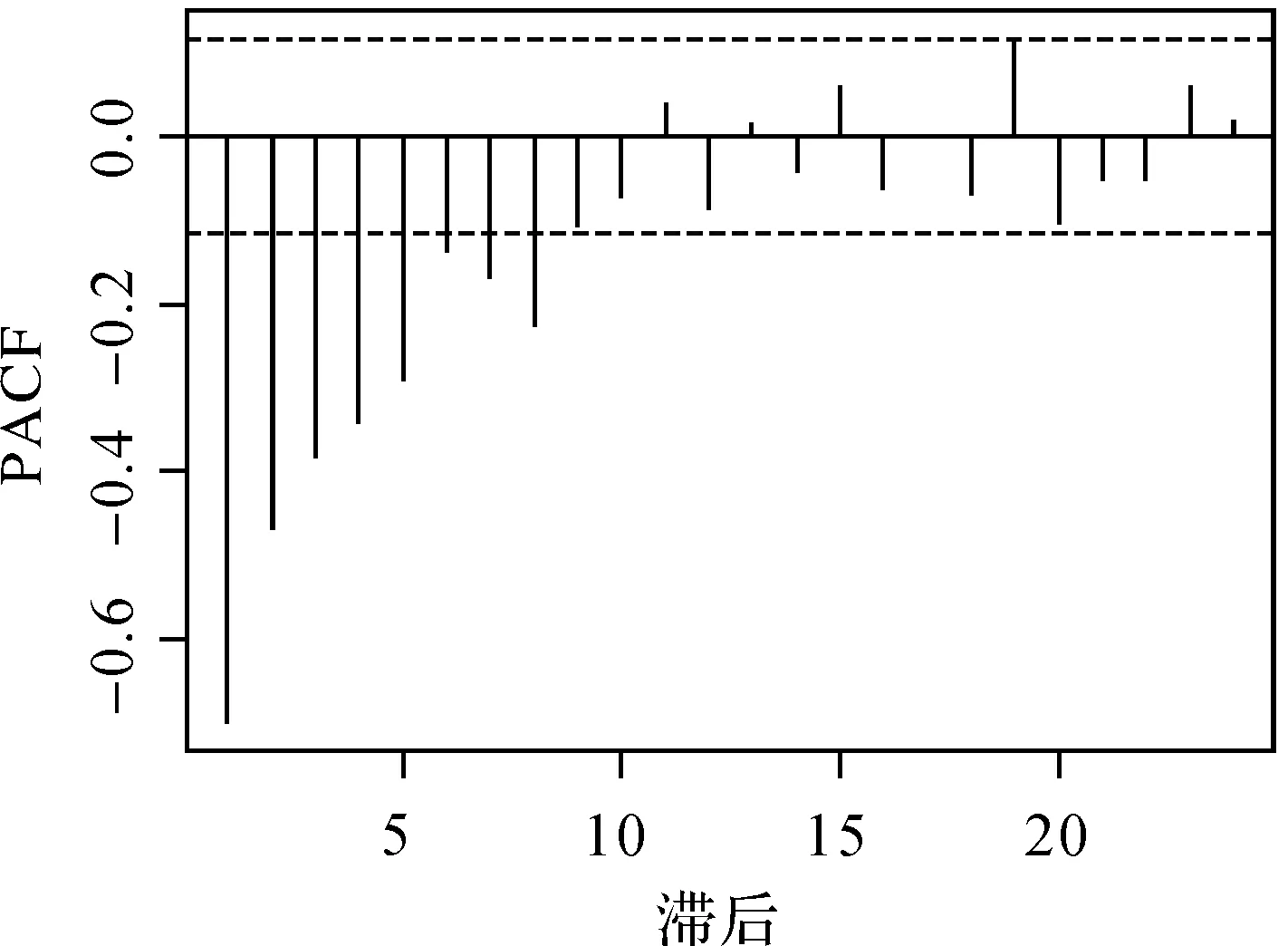
圖7 二次差分鐘差數據的偏自相關函數圖Fig.7 Sample PACF of two differences clock errors data

由自相關函數和偏自相關函數的計算結果可知，偏自相關函數在8階滯后以后截尾而自相關函數一直拖尾，故可認為兩次差分后的序列服從AR(8)模型。

3.3 異常值探測分析

計算時發現，用本文算法處理此類兩次差分后的鐘差數據時，采用5σ原則可得到很好的異常值探測效果。為驗證本文算法的有效性，在兩次差分后的第100和第200個值上分別加上其數據本身的10倍和12倍的AO類異常擾動，分別為10×1.539 32×10-10和12×2.134 291 0-10。使用本文方法對序列中的AO類異常值進行探測，則pt和wt的計算結果分別如圖8、圖9所示。

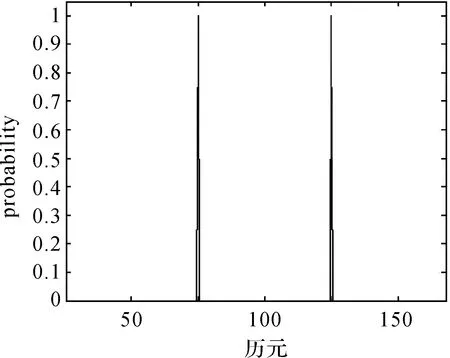
圖8 鐘差數據中單個異常擾動的pt結果Fig.8 pt of single outlier in clock errors data

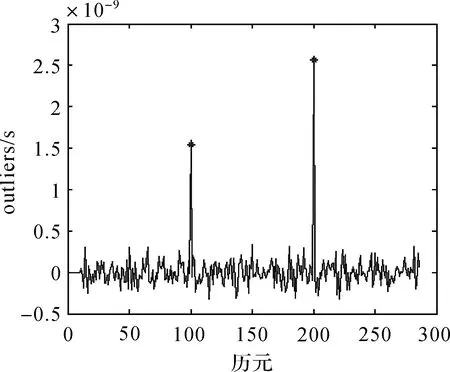
圖9 鐘差數據中單個異常擾動的wt結果Fig.9 wt of single outlier in clock errors data

由圖8和圖9可知，本文算法不但可以準確確定AO類異常值的位置，而且對相應異常擾動大小的估計也非常準確，具體異常擾動的估計值分別為：1.591 98×10-9和2.575 481×10-9。

對兩次差分后的第100—105個歷元的觀測值分別加上大小為15×10-10的AO類異常擾動，以檢驗該算法對成片AO類異常值的探測效果，其pt和wt的計算結果分別如圖10、圖11所示。

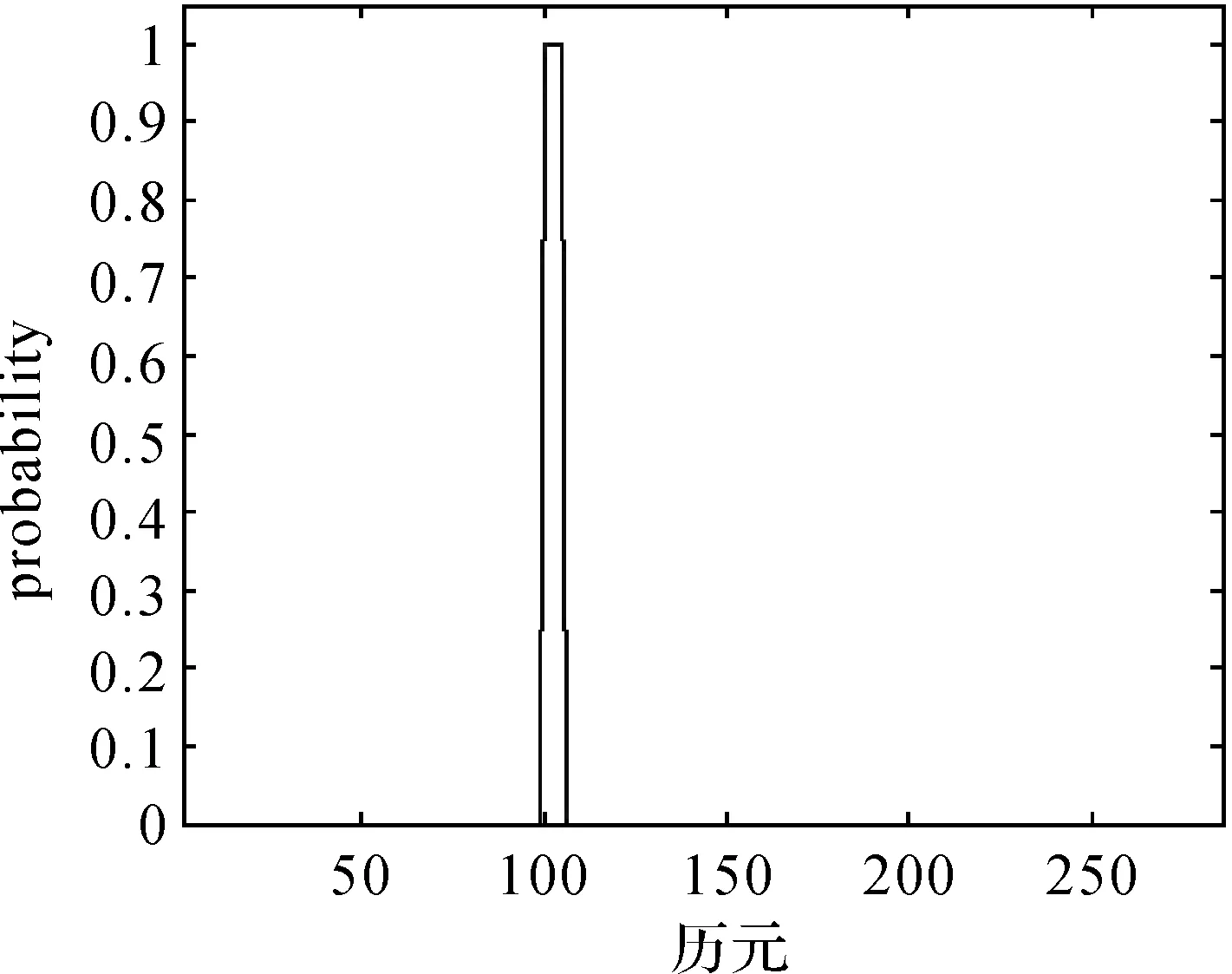
圖10 鐘差數據成片異常擾動的pt結果Fig.10 pt of patches of outliers in clock errors data

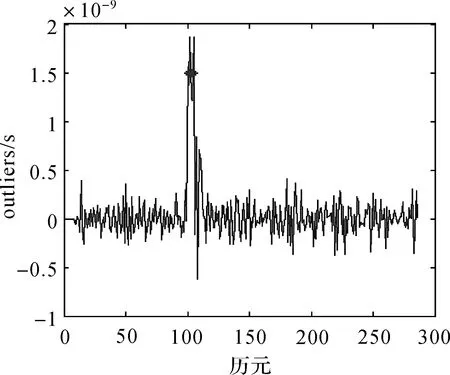
圖11 鐘差數據成片異常擾動的wt結果Fig.11 wtof patches of outliers in clock errors data

分析發現，本文方法對異常值的位置判斷非常準確，對異常擾動的大小估計稍有偏差，異常擾動大小分別被估計為15.6×10-10、13.7×10-10、18.6×10-10、12.5×10-10、12.1×10-10、18.6×10-10。異常擾動的估計值雖有偏差，但是對于如此數量級的包含成片異常擾動的數據，得到如此的估計結果已屬難能可貴。在計算過程中發現，算法具有很好的迭代穩定性，隨著迭代次數的增加，估計精度逐漸增高并趨于穩定。另外，當成片異常擾動的數值變小時，異常擾動的估計效果變差；當成片異常擾動的數值變大時，異常擾動的估計效果變好。

3.4 鐘差預報分析

差分前的IGS提供的鐘差數據如果不包含異常值，本文算法不會啟動異常擾動修復工作。此時可估計得到具體的AR(8)模型并依此對兩次差分后的鐘差數據進行預報，然后經過簡單的反差分運算即可實現衛星鐘差的預報。為了驗證算法的鐘差預報精度，利用實測數據的前200個歷元進行模型估計和異常值探測，對后88個歷元進行預報。則IGS提供的鐘差數據和預報的鐘差數據如圖12所示。為了比較兩者差異，將IGS提供的鐘差數據和預報的鐘差數據做差，其結果如圖13所示。另外，為說明本文算法的有效性，利用二次多項式方法直接對后88個歷元進行預報，給出預報結果與IGS提供的鐘差數據的做差結果如圖14所示。

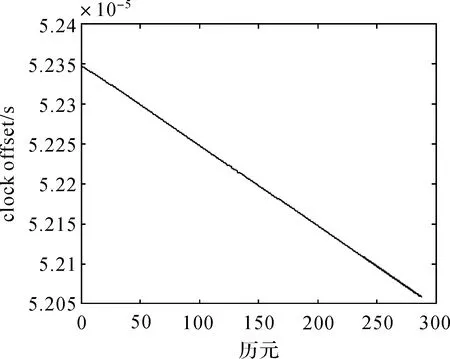
圖12 IGS提供的鐘差與預報鐘差Fig.12 Clock errors of IGS and clock errors of prediction

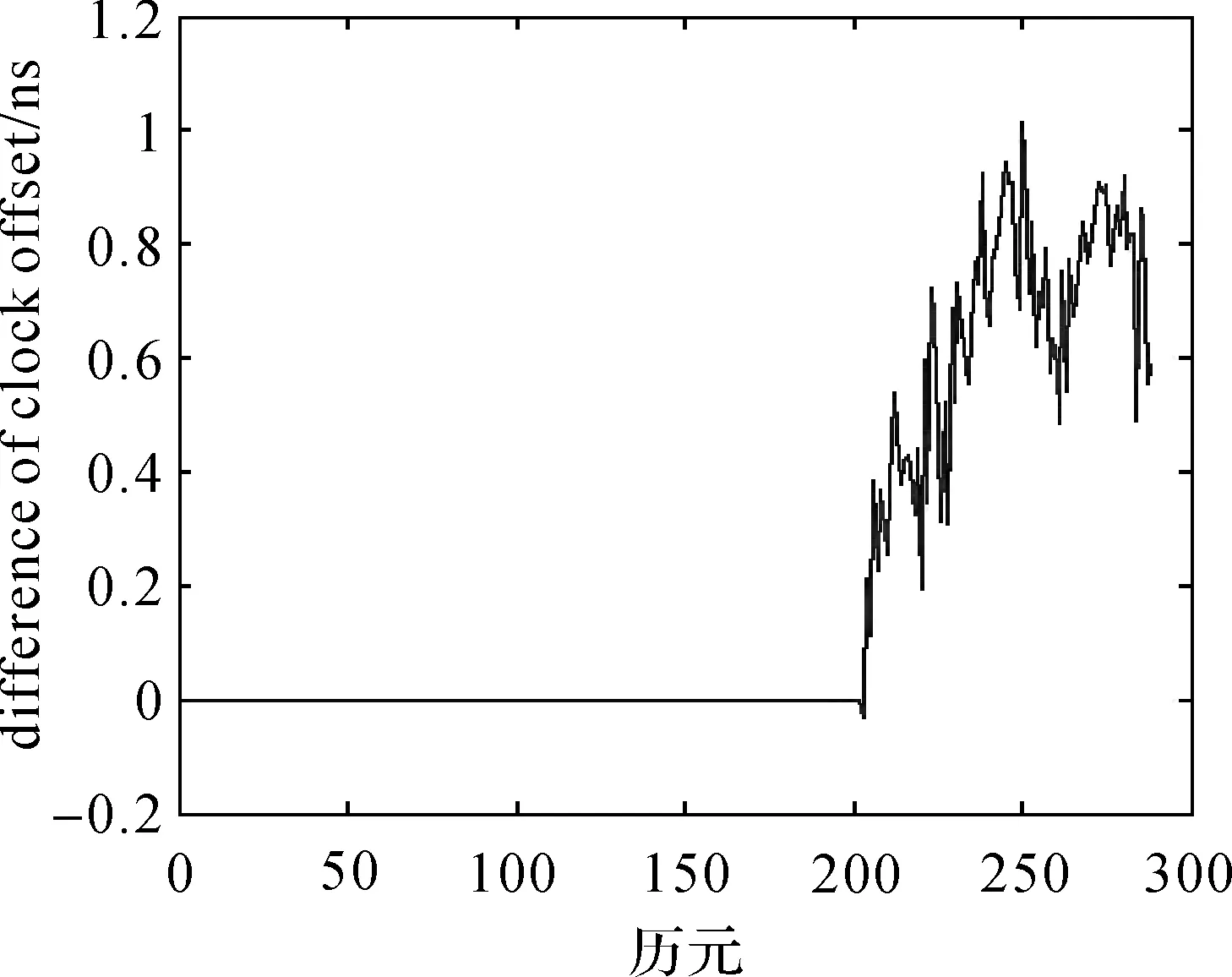
圖13 IGS提供的鐘差與預報鐘差的差Fig.13 Difference between clock errors of IGS and clock errors of prediction

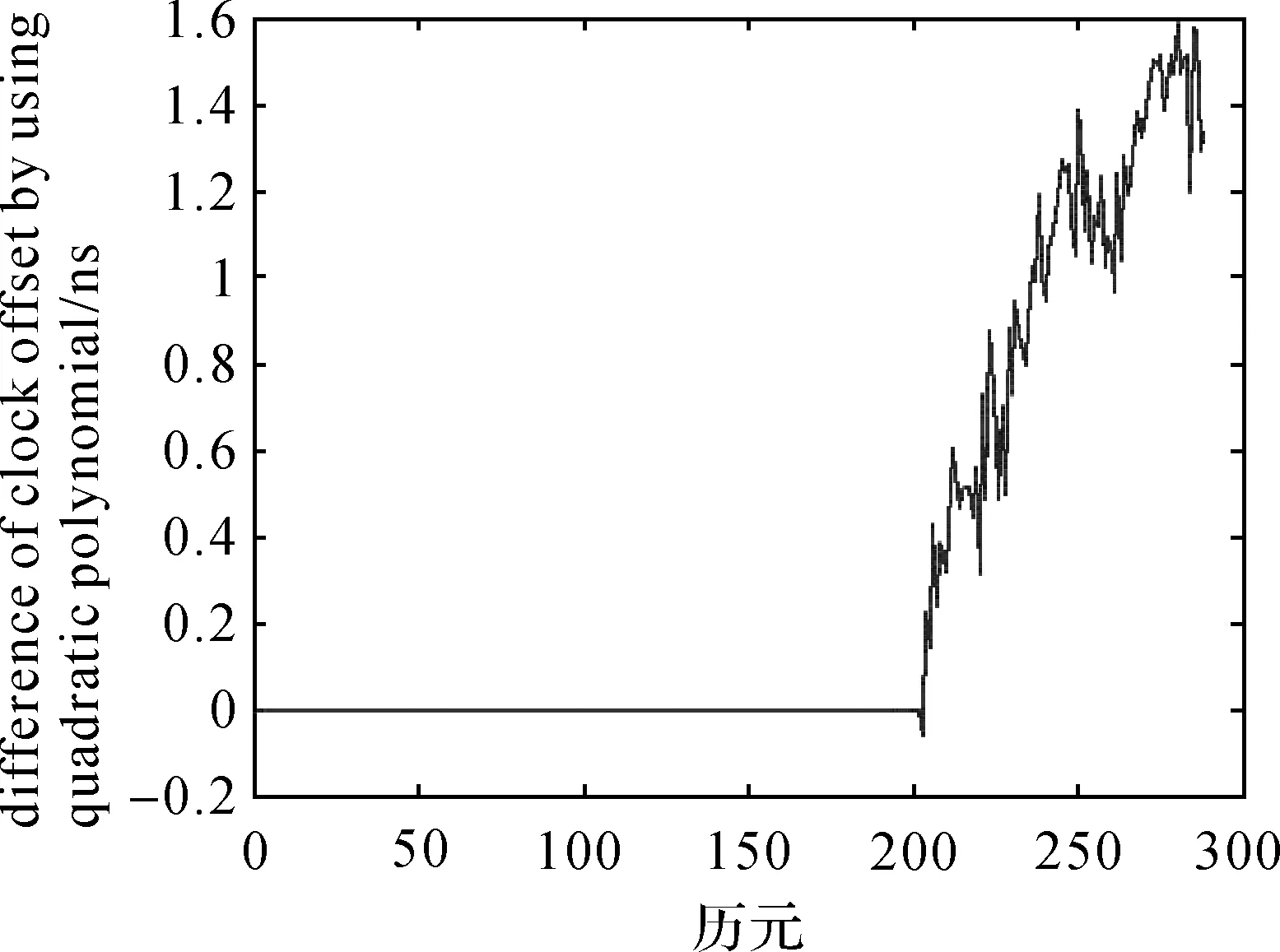
圖14 IGS提供的鐘差與多項式預報鐘差的差Fig.14 Difference between clock errors of IGS and clock errors of prediction by using polynomial

由圖12—14可以看出，沒有異常擾動時，本文算法給出的鐘差預報精度比較好。在圖12中，數據的數量級為10-5，IGS提供的鐘差數據與本文預報的后88個歷元的鐘差數據幾乎完全重合，僅能看出兩者之間微小的差異。在圖13中可以看出，相對于單位秒而言，預報的后88個歷元的鐘差數據與IGS提供的鐘差數據的差異的數量級是10-10。另外，對比圖13和圖14可以發現，本文算法的預報精度高于常用的二次多項式方法。

如果差分前的鐘差序列含有異常值，則差分后異常值會出現淹沒、掩蓋或轉移情況，使得差分后的異常值情況比較復雜。比如差分前的單個異常值，經過兩次差分之后，將變為3個位置上相鄰的成片異常值。而差分前的成片異常值，經過兩次差分后，異常值情況更復雜。此處在差分前的鐘差數據上，從第100個觀測開始加上5個異常值，異常擾動的大小約為第100個觀測值的10倍，即異常擾動的大小為5×10-4。則兩次差分后，異常值的情況變為：第98、99位置上的5×10-4與-5×10-4、第103、104位置上的-5×10-4與5×10-4。經本文算法計算后，其pt和wt的計算結果分別如圖15、圖16所示。

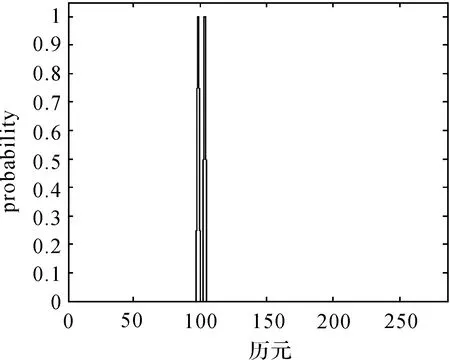
圖15 原鐘差數據成片異常擾動的pt結果Fig.15 pt of patches of outliers in original clock errors data

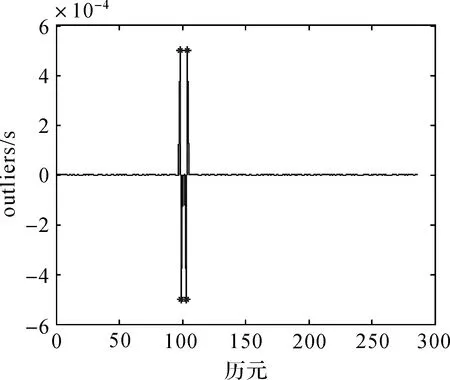
圖16 原鐘差數據成片異常擾動的wt結果Fig.16 wt of patches of outliers in original clock errors data

由圖15、圖16可以看出，本文算法的估計效果非常好，4個異常擾動的估計值分別為0.000 500 000 241 049 605，-0.000 500 000 289 798 94，-0.000 499 999 764 910 239，0.000 499 999 472 494 021。由此說明，不管差分前的異常值在差分后的平穩時間序列中如何變化，即不管差分后的平穩時間序列是包含單個異常擾動還是成片異常擾動，經過本文算法處理后均可有效消除異常值的影響。

為檢驗差分前的異常值對鐘差預報的影響，同樣從差分前鐘差數據的第100個觀測值開始加上5個大小為5×10-4的異常值，利用前200個歷元進行模型估計和異常值探測，然后對后88個歷元進行預報，并進行反差分運算。IGS提供的鐘差數據和預報的鐘差數據如圖17所示，其中在分叉處向上的曲線是異常值修正后的預報鐘差。將IGS提供的鐘差數據和預報的鐘差數據做差，其結果如圖18所示。

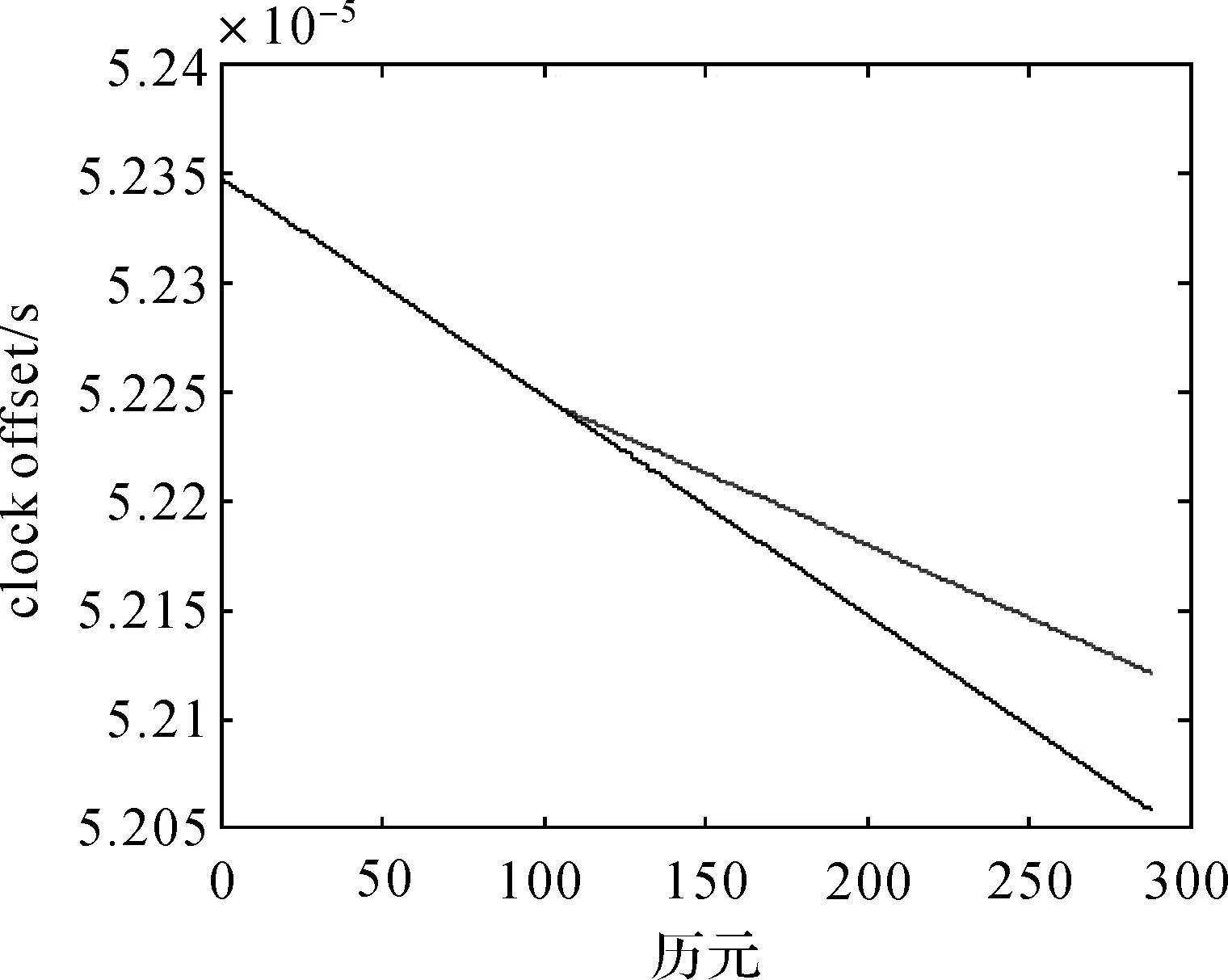
圖17 IGS提供的鐘差與含異常擾動的預報鐘差Fig.17 Clock errors of IGS and clock errors of prediction with outliers

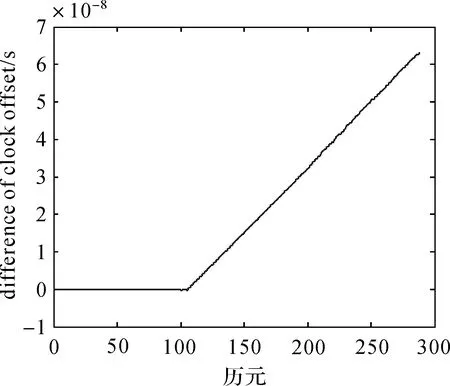
圖18 IGS提供的鐘差與含異常擾動的預報鐘差的差Fig.18 Difference between clock errors of IGS and clock errors of prediction with outliers

相對于圖12的情況，后88個歷元的鐘差預報精度降低了。從圖18可以看出，此處數據的數量級是10-8，相對于圖13中不包含異常值的情況，鐘差預報精度降低了兩個數量級。為說明此時鐘差預報精度降低的原因，對于兩次差分后的數據，修正其中異常值并預報后面數據，得到的結果如圖19所示。

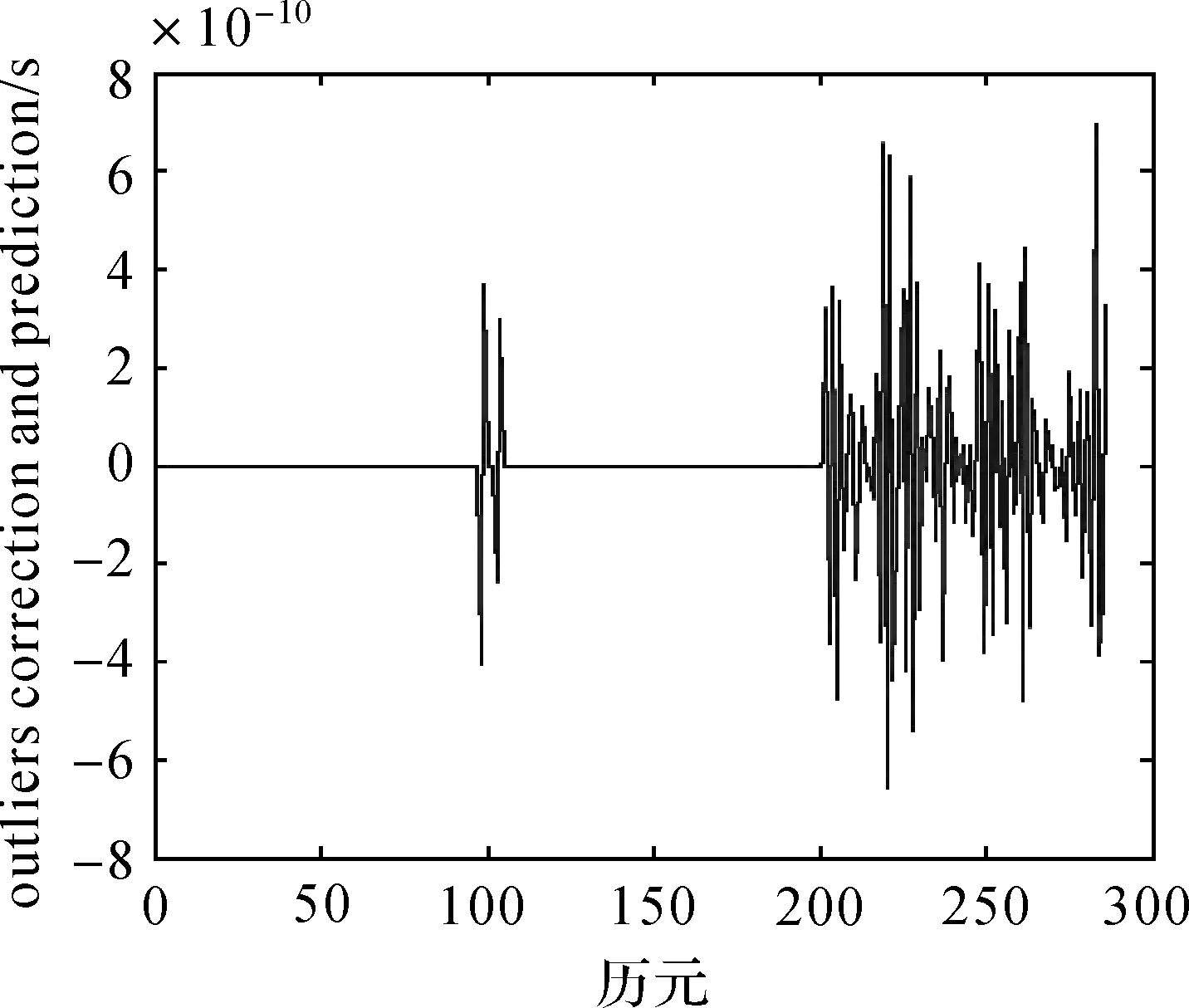
圖19 兩次差分的數據的異常值修正和預報情況Fig.19 Outliers elimination and prediction of two differences clock errors data

由圖17—圖19可以看出，雖然異常擾動大小的估計值非常準確。但是因為要經過兩次反差分運算，使得兩次反差分后得到的鐘差數據，從第100個歷元開始與IGS提供的數據出現了偏差，并且由于反差分運算的特性，這些偏差會逐步累加在反差分后的后續歷元的觀測值中。所以在鐘差數據含有異常值的情況下，即使進行了很好的異常值探測與修正，經過反差分運算后，鐘差預報的精度也會受到一定程度的影響。

由于本文算法可以很好地判定異常值位置。因此，不使用二次差分后含有AO異常值部分的數據，只利用第105個歷元以后的數據進行反差分運算，得到的鐘差預報結果如圖20所示。

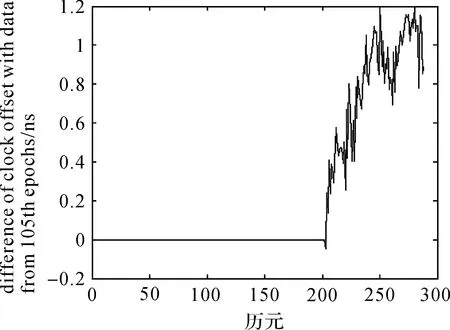
圖20 用105歷元以后數據的預報鐘差與IGS提供的鐘差的差Fig.20 Difference between clock errors of IGS and clock errors of prediction with data from 105th epochs

此結果與數據沒有異常值的鐘差預報結果非常接近。即使在數據包含異常值時，本文算法的鐘差預報結果，仍然優于數據不包含異常值時多項式算法的預報結果。

4 結 論

本文首次將EM算法應用于AR模型中AO類異常值的探測問題，并提出了相應的異常值探測與修復算法。該算法不但可以處理單個異常值問題，而且可以有效消除成片異常值的影響。本文算法有以下優點：

(1) 本文算法可以同時估計AR模型系數、噪聲方差、異常值位置和異常擾動大小，所有待估參數的估值均在同一個迭代過程中得到，具有較好的估計相容性。

(2) 本文算法有效解決了成片AO類異常值探測問題。只要σ的倍數選擇得當，本文算法可以有效避免出現掩蓋和淹沒現象。

(3) 每一步迭代過程中均對原始觀測進行修正得到純凈數據，并與原始數據共同參與估計的迭代過程，進而可以得到更準確的模型系數、噪聲方差和異常擾動的估計值。

(4) 在異常擾動的判定過程中，不僅考慮了估計的異常擾動大小，而且考慮了估計的噪聲方差，充分利用了異常擾動的相關統計信息。

(5) 本文算法的迭代穩定性良好，一般經過較少的迭代即可得到最終估計結果，隨著迭代次數的增加，算法逐步收斂于函數極值，很少出現迭代發散的情況。

(6) 本文對于仿真數據采用的是3σ原則，對于實測的GPS鐘差數據采用的是5σ原則。根據問題的具體情況，應當選擇合適的σ原則的倍數，進而有效拓展該算法的使用范圍。

在算法的實用性方面，本文將該算法應用于衛星鐘差的異常擾動處理。采用本算法處理的衛星鐘差觀測序列，可以準確探測出觀測序列中的AO類異常值，并同時擬合得到精確的AR模型，從而實現了對衛星鐘差的高效、快速預報。