深水鉆井隔水導管承載能力影響因素分析

劉清友， 秦 松， 毛良杰， 王國榮

（1. 油氣藏地質及開發(fā)工程國家重點實驗室（西南石油大學），四川成都 610500；2. 西南石油大學能源裝備研究院，四川成都610500）

深水鉆井中，水下井口及隔水導管受到的載荷非常復雜。軸向外載荷主要來自裝備自身的重力和撓性接頭傳遞的軸向載荷，井口還受到來自防噴器組頂部撓性接頭傳遞的橫向與軸向載荷[1-2]。此外，海流也會對井口產生橫向載荷。深水鉆井中，由于海底井口失穩(wěn)造成隔水導管變形而導致的安全問題時有發(fā)生，而且結果往往較為嚴重，有時甚至會使整口井報廢。因此，分析深水鉆井中隔水導管的承載能力具有現(xiàn)實意義。

目前，深水鉆井隔水導管力學分析已成國內外研究的重點，但研究主要集中在隔水管的變形、等效應力隨管身分布情況和剩余壽命等方面，關于井口以深隔水導管承載能力方面的研究則較少[3-5]。雖然有人研究指出深水鉆井隔水導管可能存在失穩(wěn)甚至報廢風險，但并沒有建立相應的理論體系。例如，G. W. King[6]采用有限元方法對深水鉆井中隔水導管的穩(wěn)定性及井口疲勞失穩(wěn)問題進行了研究，但沒有建立起相應的理論；R. Juiniti 等人[7]總結了Campos 盆地深水鉆井作業(yè)中有關海底井口力學穩(wěn)定性的經驗教訓，探討了不同水深條件下不同尺寸隔水導管的穩(wěn)定性，但未形成理論體系；Guan Zhichuan 等人[8]采用有限差分法對淺部隔水管柱以及海底井口的側向偏移進行了靜力學數(shù)值求解，求解時考慮了管柱軸向力的影響，但未涉及井口以深隔水導管的穩(wěn)定性問題；蘇堪華等人[9]利用土力學樁基理論中的地基反力 p-y曲線研究了深水鉆井井口的穩(wěn)定性，但對受力進行簡化后忽略了橫向載荷，且認為海底土壤性質恒定不變，與實際情況有較大出入；張偉國等人[10]利用有限元方法計算分析了隔水導管出泥高度對井口穩(wěn)定性的影響，但建立的模型較為粗略，考慮的影響因素較少，計算結果精度不高；周正波[11]研究了鉆井液穩(wěn)定循環(huán)和力學穩(wěn)定條件下的井口穩(wěn)定性，但模型建立在特定地層基礎之上，不具有普適性。為了解決井口以深隔水導管的穩(wěn)定性問題，深入分析深水鉆井隔水導管承載能力的影響因素及影響規(guī)律，筆者采用力學等價轉化計算方法，將深水井口上部的防噴器組及隔水管下部撓性接頭對井口的作用力進行傳遞簡化，然后考慮隔水導管受到橫向與軸向載荷的作用，采用ANSYS 建立管-土應力作用和變形過程的模型，并通過算例分析了井口作用力、隔水導管外徑和壁厚、井口出泥高度及地基類型對隔水導管承載能力的影響，以期為現(xiàn)場施工及相關理論研究提供指導。

1 井口受力分析

深水鉆井作業(yè)系統(tǒng)的主要組成如圖1 所示，其中，隔水管是重要部件，除了承受井口防噴器的重力以外，還直接承受下入井中的鉆柱的浮重；同時，隨著隔水管長度增大，由海流產生的橫向作用力也隨之增大；而且，其通過隔水管底的撓性接頭傳遞加到海底井口及下部導管上，對井口及隔水導管產生不可忽視的軸向及橫向作用力[12-13]。對于一些特定海域，如南海海域，海底土通常為淤泥和沉積物，塑性較高，密度較低，含水量和孔隙度比通常情況下要高，故其對隔水導管的地基反力相比陸地更不穩(wěn)定[14]。

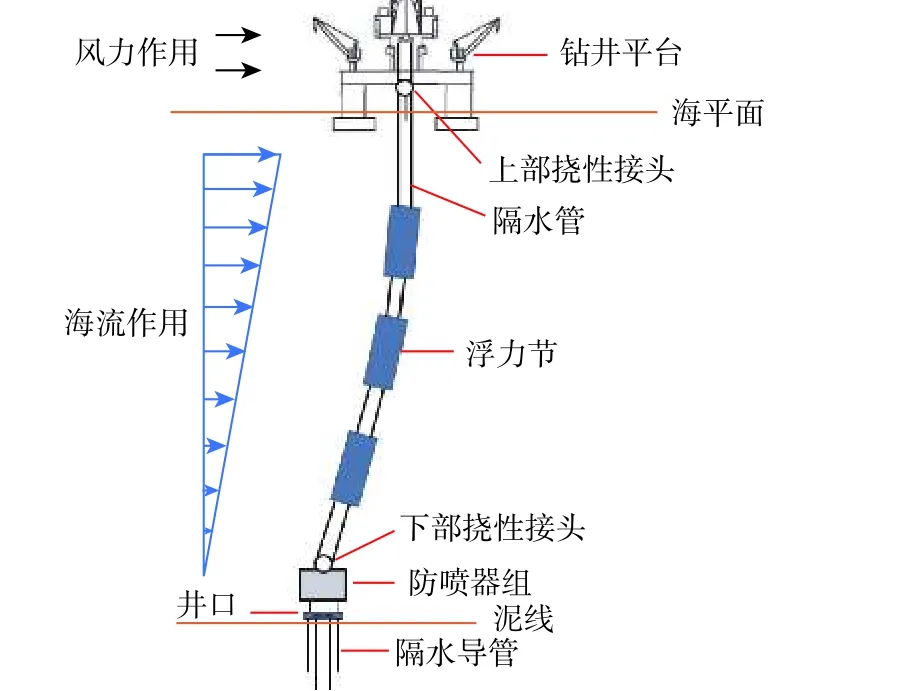
圖 1 深水鉆井作業(yè)系統(tǒng)示意Fig. 1 Schematic diagram of deepwater drilling system

對井口以上的裝置對井口施加的外載荷向井口進行等效轉化，就可以在不同工況下采用相同模型進行隔水導管承載能力分析，其簡化情況如圖2所示（圖2 中： fr， fb和 fw分別為海流施加給隔水管、重型防噴器組和井口的橫向載荷，kN； ff， Ff分別為通過隔水管底的撓性接頭傳遞給井口的橫向載荷和軸向載荷，kN； Fr， Fb和 Fw分別為隔水管、重型防噴器組和井口的浮重，kN）。對井口的受力情況進行簡化，從而為建模提供基礎。

根據(jù)作用力與反作用力的原理進行簡化[15]，其力學等效轉化公式為：

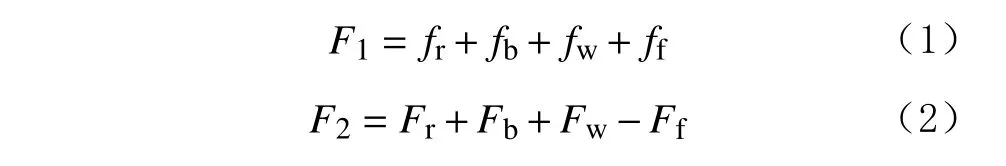
式中：F1為井口承受的等效橫向載荷，kN；F2為井口承受的等效軸向載荷，kN。

2 隔水導管承載能力分析模型

為了使模型計算時更易于收斂，建立模型前首先進行合理假設：1）由于隔水導管長度與其橫截面積相差極大，所以忽略其底端與土壤接觸產生的承載力，近似認為支撐力主要來源于管側與土壤的靜摩擦力；2）隔水導管為各向同性、均質、線彈性鋼制管柱，且管段接頭的局部影響可以忽略不計；3）隔水導管在重力和外部作用力的共同作用下只發(fā)生微小變形。

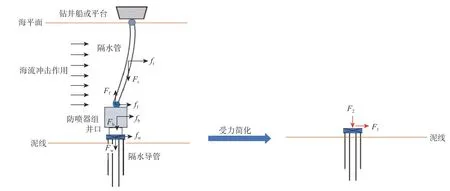
圖 2 深水鉆井中井口受力簡化示意Fig.2 Simplified schematic of wellhead force conditions in deepwater drilling

根據(jù)式（1）和式（2），結合以上假設條件，在ANSYS 中建立三維有限元模型，分析隔水導管耦合受力情況下的力學響應情況。由于模型是對稱的，因此使用對半模型進行分析。隔水導管采用單元庫中適合模擬線性、彎曲及適當厚度的Shell 43 單元進行模擬；根據(jù)海底地層的性質，土壤采用Drucker-Prager 模型進行模擬。

分別建立土壤模型和隔水導管模型。建立土壤模型時，設置擾動半徑為50 倍管徑，影響深度為30.00 m。分別對管與土壤設定相應的約束條件：模型底部限制3 個方向（x 軸、y 軸和z 軸方向）的位移，土壤周邊分別限制其在x 軸和y 軸上的位移，模型的對稱面限制其在y 方向上的位移。設定2 個接觸對，即導管側-井壁接觸和導管端-井底面接觸。施加橫向與軸向載荷時，其受力端面均為導管上部截面。

對土壤模型劃分網(wǎng)格時，重點加大井筒附近海底土的網(wǎng)格數(shù)量，劃分結果如圖3 所示。隔水導管共劃分328 個網(wǎng)格，海底土共劃分15 224 個網(wǎng)格。

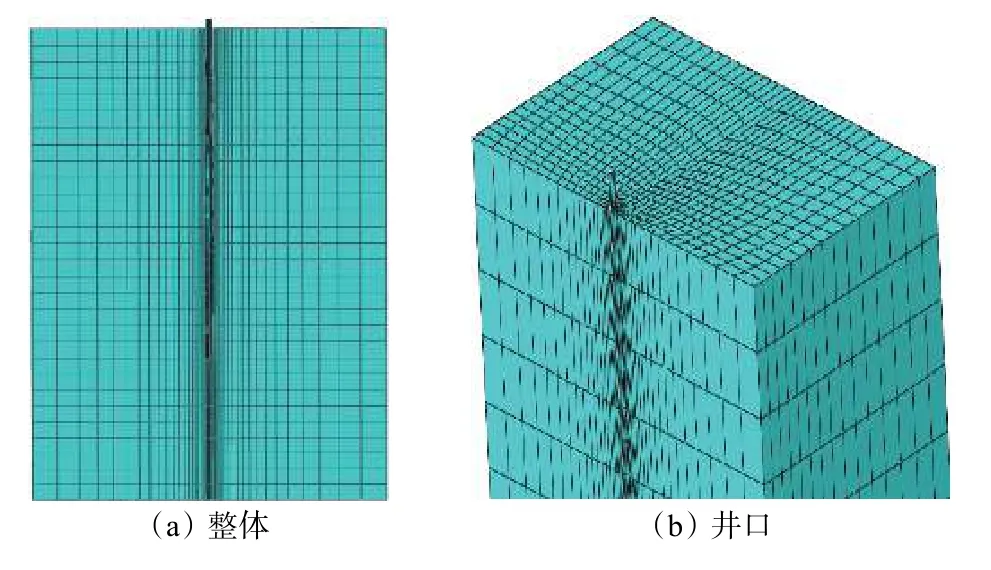
圖 3 深水鉆井井口三維有限元模型示意Fig. 3 3D finite element model of a deepwater drilling wellhead

3 算例及影響因素分析

3.1 隔水導管及地層參數(shù)設置

基于上文建立的模型，以南海某區(qū)塊為例進行實例計算。隔水導管的彈性模量取210 GPa，泊松比取0.3[11]。結合該區(qū)塊具體的地質參數(shù)，在ANSYS中將土壤分成7 層進行有限元建模，各層的土質參數(shù)見表1。其中，頂部2 層海底土彈性模量取2 MPa，3—7 層彈性模量取10 MPa，泊松比取0.4。

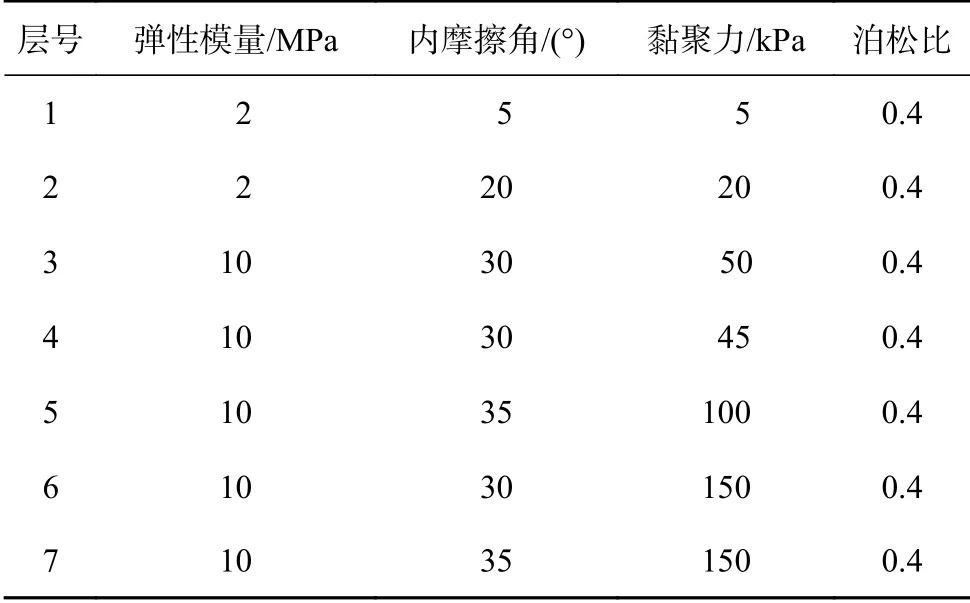
表 1 南海某區(qū)塊各層的土質參數(shù)Table 1 Soil parameters of each formation in a block in the South China Sea

3.2 井口載荷計算

目前，隔水導管大多采用噴射方法下入。隔水導管下入之后，在軸向上承受一系列復雜的載荷，這些載荷在不同工況下會有較大變化。如果導管柱的軸向承載能力不夠，管柱就會下陷甚至失穩(wěn)，最終導致整口井報廢。其中，最危險的工況（軸向載荷最高）發(fā)生在安裝隔水管和防噴器組之前，如圖4 所示（圖4中： Fc為某時刻隔水導管的管側阻力，kN； Fd為某時刻隔水導管的管端阻力，kN）。表層套管懸掛在井口上，所有軸向作用力均由隔水導管承載[16-17]。

隔水導管的初始承載能力計算公式為：

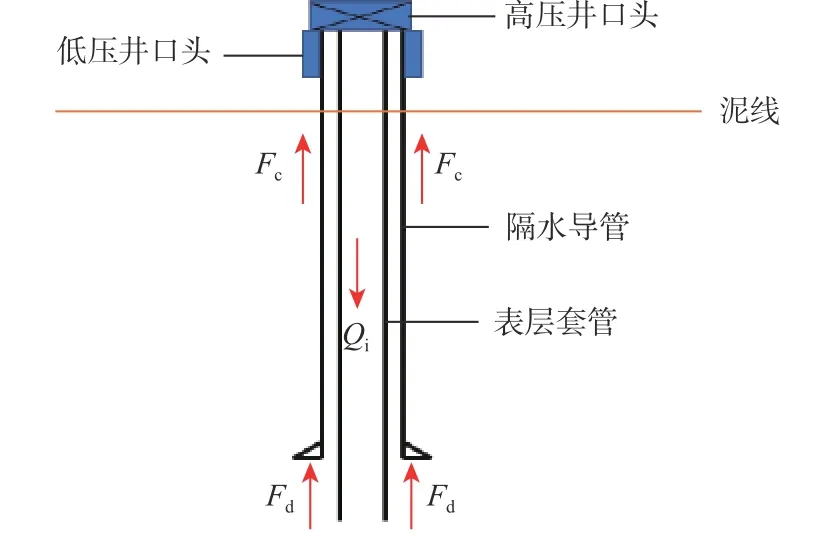
圖 4 最危險工況時的隔水導管受力示意Fig. 4 Schematic of conductor stress states under the most risky conditions

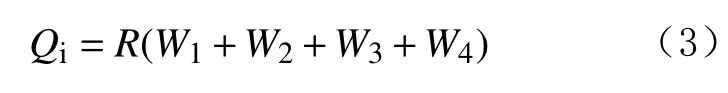
其中

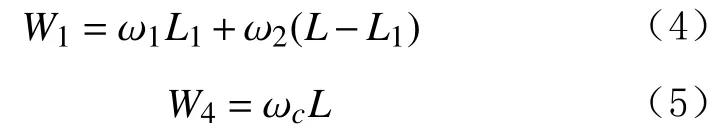
當阻力與初始承載能力達到平衡時，有：

式中： Qi為初始承載能力，kN；R 為鉆壓利用率，一般為0.8～1.0； W1為 隔水導管浮重，kN； W2為低壓井口頭在海水中的浮重，kN； W3為噴射鉆具在海水中的浮重，kN； W4為 導管送入工具的浮重，kN； ω1為38.0 mm厚鋼材單位長度的浮重，kN/m； ω2為25.0 mm 厚鋼材單位長度的浮重，kN/m； L1為38.0 mm 厚鋼材的長度，m； L為隔水導管的設計下深，m； ωc為噴射鉆具單位長度的浮重，kN/m。

表2 和表3 分別為南海某區(qū)塊3 口井的鉆井施工參數(shù)與套管下入層序，結合式（3）—式（6），計算出3 口井井口所受軸向載荷情況（見表4）。

表 2 南海某區(qū)塊鉆井施工參數(shù)Table 2 Drilling parameters of a block in the South China Sea

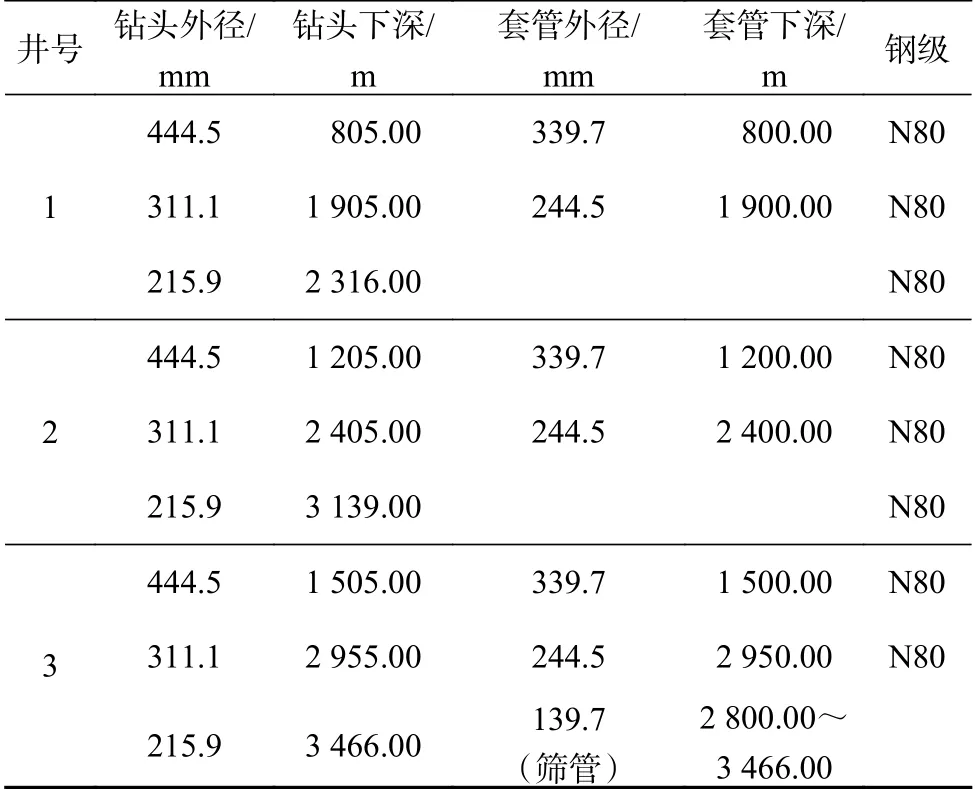
表 3 南海某區(qū)塊套管下入層序Table 3 Casing program of a block in the South China Sea

根據(jù)該區(qū)塊當前的風浪流作用特點，設水下井口在海洋環(huán)境極端惡劣情況下的最大橫向壓力為1.2 MPa[15]。通過上述計算分析，分別得到了水下井口所承受的橫向及軸向載荷，并以此作為后續(xù)分析中設置參數(shù)的基準數(shù)據(jù)，進而開展影響因素分析。

3.3 影響因素分析

3.3.1 井口所受載荷

利用已經建立的三維有限元模型，結合該區(qū)塊中井口的受力特點，對隔水導管頂部截面施加剪切形式的橫向壓力與法向壓力，模擬參數(shù)見表5，井口所受作用力對隔水導管橫向位移與Mises 應力的影響如圖5 所示。

對A1、A2 和A3 組進行對比，發(fā)現(xiàn)：1）保持軸向壓力不變，增大橫向壓力，隔水導管上部的橫向位移逐漸增大，如圖5（a）所示；2）橫向壓力除了引起隔水導管橫向位移的變化，還會影響隔水導管的Mises 應力，如圖5（b）所示。隨著橫向壓力增大，Mises 應力峰值明顯增加，表明井口受到的橫向壓力對Mises 應力峰值有顯著影響；同時，對比3 條曲線發(fā)現(xiàn)，井口橫向壓力的變化對隔水導管橫向位移及Mises 應力分布的影響比較小，兩者均在增大到峰值后迅速單調減小，不同橫向壓力下的橫向位移及Mises 應力收斂的位置均相同，Mises應力峰值也出現(xiàn)在同一深度（10 m 左右）。

表 4 南海某區(qū)塊井口軸向載荷計算Table 4 Calculation on the wellhead axial loads of a block in the South China Sea

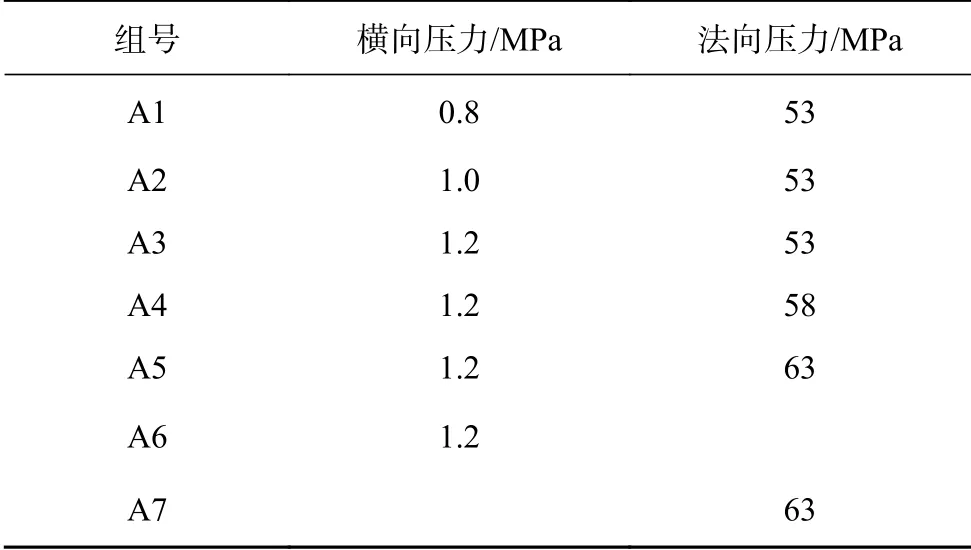
表 5 表面牽引力與法向壓力設置Table 5 The setting of surface traction and normal pressure

對A3、A4 和A5 組進行對比，發(fā)現(xiàn)：1）在橫向壓力相同的情況下，軸向壓力的變化對隔水導管橫向位移影響甚微，如圖5（c）所示；2）同時，在橫向壓力相同的情況下，隨著軸向壓力增大，隔水導管的Mises 應力出現(xiàn)了顯著變化，相同深度的Mises 應力都顯著增大，應力峰值也顯著升高，如圖5(d)所示。但值得注意的是，Mises 應力沿管身的分布趨勢基本相同，峰值深度以及收斂深度均相同。

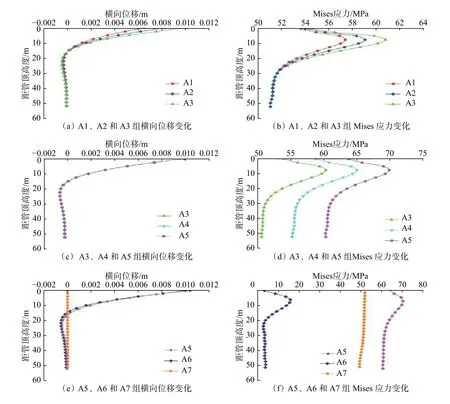
圖 5 井口所受載荷對隔水導管橫向位移與Mises 應力的影響Fig.5 Effect of wellhead force on Mises stress and lateral displacement of riser

對比分析圖5（a）、圖5（b）、圖5（c）和圖5（d）發(fā)現(xiàn)，管身橫向位移和Mises 應力在一定深度下基本保持不變，井口所受橫向壓力與軸向壓力的作用效果主要集中在隔水導管的上部區(qū)域，對隔水導管下部影響甚微。因此，實際施工時要重點關注隔水導管上部的受力情況，采取適當方法增大上部導管強度，避免其因受力過大而失效，從而保證鉆井作業(yè)安全。

增添了A6 和A7 作為對照組，作進一步分析。A6 組只作用最大表面牽引力，A7 組只作用最大法向壓力，結果見圖5（e）和圖5（f）。由圖5（e）可知，只有法向壓力作用時，橫向位移無變化，始終保持為零；只有橫向壓力作用時，橫向位移分布與耦合時基本一致，說明法向壓力對橫向位移的影響甚微。由圖5（f）可知，只有法向壓力作用時，Mises 應力分布雖然與耦合時一致，但其數(shù)值大大減小，峰值應力僅為耦合情況下的22%，隔水導管下部平均應力僅為3 MPa 左右；只有橫向壓力作用時，Mises 應力變化幅度很小，僅為峰值應力的3%，以上分析結果均不符合實際情況。

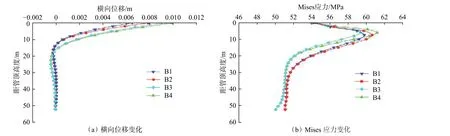
圖 6 隔水導管外徑和壁厚對橫向位移與Mises 應力的影響Fig.6 The effect of conductor outer diameter and wall thickness on the Mises stress and lateral displacement of conductor body

綜上可知，采用耦合模型進行分析能夠得到較為明顯的隔水導管橫向位移及Mises 應力變化，貼近現(xiàn)場施工實際情況，對現(xiàn)場施工更具指導作用。

3.3.2 隔水導管直徑與壁厚

以隔水導管的外徑和壁厚作為研究對象，分析其對井口穩(wěn)定性的影響，數(shù)據(jù)設置見表6，隔水導管外徑和壁厚對橫向位移與Mises 應力的影響如圖6 所示。

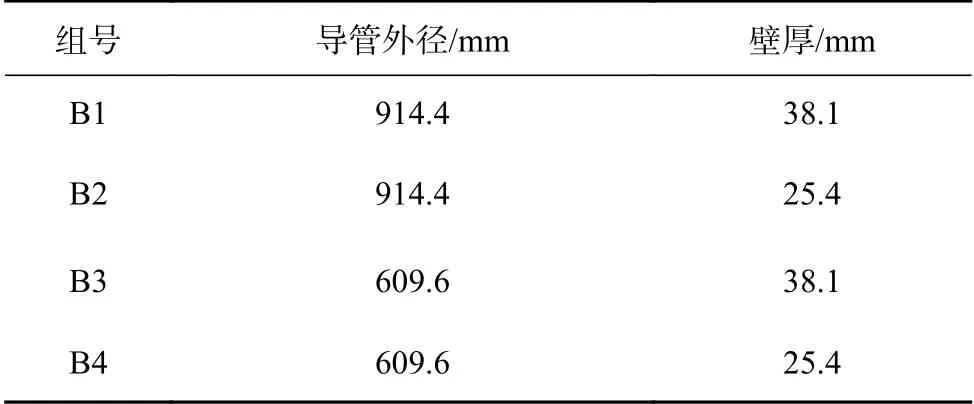
表 6 隔水導管外徑和壁厚Table 6 The outer diameter and wall thickness of conductor

由圖6（a）可知：隔水導管壁厚保持不變，隔水導管外徑增大，隔水導管橫向位移逐漸減小；隔水導管外徑保持不變，隔水導管壁厚增大，隔水導管的橫向位移逐漸減小，說明其抗彎能力逐漸增強。由圖6（b）可知：井口橫向載荷和軸向載荷保持在一定范圍的情況下，隔水導管外徑和壁厚的變化對沿管身的Mises 應力分布趨勢影響較小；壁厚變化時，Mises 應力峰值變化更加顯著，說明與隔水導管外徑相比，壁厚對Mises 應力峰值的影響更加明顯。因此，實際施工時可以適當增大隔水導管靠近井口部位的外徑和壁厚，從而增強隔水導管的承載能力，提高井口的穩(wěn)定性。

3.3.3 井口出泥高度和地基類型

以井口的出泥高度和海底地基類型為研究對象，分析其對井口穩(wěn)定性的影響，基本參數(shù)設置見表7，井口出泥高度和地基類型對隔水導管橫向位移與Mises 應力的影響如圖7 所示。

由圖7 可知：保持地基類型一致，井口距泥線的高度增大，隔水導管上部的橫向位移和Mises 應力也相應增加，表明海底水流對井口的沖擊會顯著影響水下井口的穩(wěn)定性；地基類型為黏性土時的隔水導管上部橫向位移和Mises 應力均比地基類型為砂性土時要大；隔水導管在黏土中受到井口載荷影響的長度要比在砂性土中大。因此，深水鉆井時要結合該區(qū)塊的地質特點設置合理的井口出泥高度，力求做到經濟合理，兼顧成本與安全。

表 7 井口出泥高度和地基類型Table 7 The wellhead above-mudline height and foundation type

3.3.4 入泥深度

以隔水導管的入泥深度為研究對象，分別設置隔水導管入泥深度為20.00，30.00，40.00，50.00，60.00 和70.00 m，分析其對井口穩(wěn)定性的影響，結果如圖8 所示。

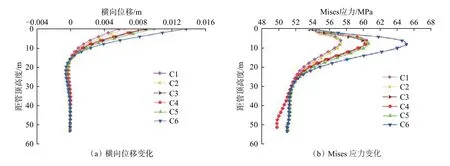
圖 7 井口出泥高度和地基類型對隔水導管橫向位移與Mises 應力的影響Fig.7 Effects of wellhead above-mudline height and foundation type on the Mises stress and lateral displacement of conductor

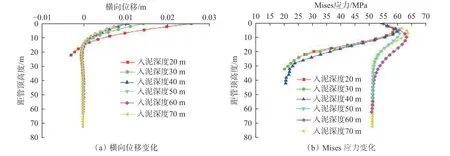
圖 8 隔水導管入泥深度對橫向位移與Mises 應力的影響Fig.8 Effect of the driving depth of conductor on the Mises stress and lateral displacement of conductor bodies

由圖8（a）可知：隨著隔水導管下入深度增大，井口處的橫向位移逐漸減小；入泥深度為40.00～70.00 m 時井口處橫向位移的增幅很小；但入泥深度由40.00 m 減至30.00 m 時井口處的橫向位移突然增大。由此推測，在此地質條件下隔水導管最小入泥深度應為30.00～40.00 m。由圖8（b）可知：隔水導管入泥深度為20.00～40.00 m 時，隨著入泥深度增加，Mises 應力并不會收斂于一個定值，而是一直減小至管底；入泥深度增大到50.00 m 時，Mises 應力就會向同一深度處收斂。

有限元分析結果表明，隔水導管的入泥深度對其在井口處的橫向位移與Mises 應力影響明顯，若下入深度過小，會造成在極限工況下橫向位移過大，導致井口失穩(wěn)；若下入深度過大，又會造成施工成本升高。因此，深海鉆井時需要確定經濟合理的隔水導管入泥深度。

4 結 論

1）井口橫向載荷是影響隔水導管橫向位移的主控因素，而軸向載荷對隔水導管的橫向位移作用并不顯著；隨著入泥深度增加，隔水導管橫向位移逐漸減小，而Mises 應力則先增大后減小，其中位移和應力在隔水導管入泥深度10.00 m 左右存在拐點，故可以在一定深度以淺加大管柱的外徑及管壁厚度，以提高隔水導管在耦合作用力下的穩(wěn)定性；不同地基力學性能對隔水導管位移及應力分布的影響極其明顯，隔水導管在砂性地基中的承載能力較黏性地基中要高。

2）隔水導管入泥深度存在臨界值，當入泥深度小于臨界值時，橫向位移和Mises 應力變化都會對隔水導管承載能力造成惡劣影響，故可采用此模型進一步研究確定經濟合理的下入深度，為現(xiàn)場施工提供指導。

3）深水鉆井中，井口受到上部加大加重防噴器組的重力、隔水管底部撓性接頭傳遞載荷、海流以及鉆井船或鉆井平臺的共同作用，故合理設置隔水導管頂部的張緊力和鉆井平臺或鉆井船的漂移數(shù)值，可以進一步提高深水鉆井中隔水導管的穩(wěn)定性。