塔河油田靶向壓裂預制縫轉向技術模擬研究

房好青， 趙 兵， 汪文智 ， 周 舟

（1. 中國石化西北油田分公司石油工程技術研究院，新疆烏魯木齊 831000；2. 油氣資源與探測國家重點實驗室（中國石油大學（北京）），北京 102249；3. 中國石油大學（北京）石油工程學院，北京 102249）

塔河油田是我國目前發現的規模最大的海相巖溶縫洞型碳酸鹽巖油氣藏，其儲層基質十分致密，基本不具備油氣滲流的條件。儲層主要的儲油空間為天然孔洞和裂縫，因此需要通過水力壓裂創造滲流通道。傳統壓裂裂縫一般沿最大水平主應力方向延伸，但是為了溝通位于非主應力方向的儲集體，應用預處理造縫技術在井周形成方向可控、長度確定的預制縫，然后結合碳酸鹽巖儲層裂縫延伸轉向機理，可以控制人工裂縫轉向，從而溝通更多的儲集體。

目前國內外在靶向壓裂裂縫轉向技術研究方面仍處于探索階段。張廣清等人[1-3]基于有限元三維應力分析，研究了定向射孔下水力裂縫起裂機理，建立了任意形狀裂縫應力強度因子的確定模型；張洪新等人[4]建立了壓裂裂縫轉向的應力場和滲流場數值模型，對壓裂裂縫轉向機理進行了定量研究；黃高傳等人[5]為提高老井重復壓裂效果，對暫堵裂縫轉向情況進行了研究分析；C. A. Wright 等人[6]分析了應力干擾源對裂縫轉向的影響，發現誘發轉向的應力變化不是純彈性，裂縫可能會發生不對稱擴展；盧運虎、陳勉等人[7-8]對頁巖氣儲層水力裂縫的擴展與轉向擴展機制進行了研究，推導出了三維空間中水力裂縫激活和轉向控制方程。綜合來看，對于地層中裂縫轉向問題的研究大多局限于力學分析，但碳酸鹽巖油氣儲層靶向壓裂的轉向結果不僅與裂縫在地層中擴展的力學因素有關，也受井筒沿程摩阻以及裂縫縫內壓力損耗的影響，僅模擬裂縫尖端轉向的模型難以為整體靶向壓裂施工提供依據和參考。

為此，筆者根據實際施工流程，對井筒段壓力計算模型、裂縫內壓力損耗計算模型及靶向壓裂裂縫轉向模型進行耦合，形成了從井口到裂縫尖端的一體化解析模型，模擬了靶向壓裂裂縫在地層中的擴展、延伸和轉向情況，并分析了各施工參數對靶向壓裂裂縫轉向距離的影響規律，以期指導縫洞型碳酸鹽巖儲層的現場壓裂施工，提高勘探開發效果。

1 碳酸鹽巖儲層預制縫轉向模型

建立模型時，首先進行以下假設：1）壓裂液在流動過程中固體顆粒脫離管壁，流動液體在管壁上為層流狀態下的黏彈性液體，而流動中心顆粒的濃度和雷諾數較高，形成了高濃度的流核；2）儲層上下為不滲透邊界，裂縫與井筒相對稱，不計裂縫寬度，忽略毛細管壓力和重力的影響；3）只有縫內壓力在縫端產生奇異性，外部應力場并不直接影響應力強度因子，只有通過改變縫內虛擬力來影響應力強度因子。

1.1 井底壓力計算模型

管內產生阻力的原因：首先，流體流動中永遠存在著質點的摩擦和撞擊現象，質點摩擦所表現出來的黏性及質點發生撞擊引起流動速度變化所表現出來的慣性，是產生沿程摩阻的根本原因；其次，由于管壁的限制，液流與管壁接觸，發生摩擦與撞擊，消耗能量形成阻力。筆者采用劉合等人[9-10]對D. L.Lord 和J. M. McGowen 根據實驗數據回歸擬合公式的修正公式：

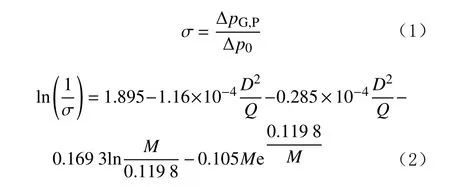
式中： σ為降阻比； Δp0為清水的管柱沿程摩阻，Pa；ΔpG,P為壓裂液的管柱沿程摩阻，Pa；D 為管柱的直徑，m；Q 為排量，m3/min；M 為稠化劑的質量濃度，kg/m3。

對式（2）進行自然對數轉換，可計算出管柱沿程摩阻降阻比 σ，從而得到管柱沿程摩阻，然后根據井筒壓力關系計算井底壓力：

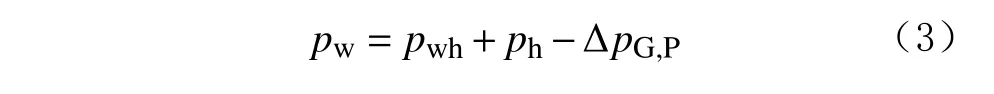
式中：pw為井底壓力，MPa；pwh為井口壓力，MPa；ph為液柱壓力，MPa。

將pw的計算結果代入垂直裂縫不穩定滲流壓力計算模型中，進行無因次處理后，通過Laplace 變換計算分析裂縫中壓力的變化規律。

1.2 裂縫段壓力分布計算

壓裂過程中裂縫內的壓力并不是常數，裂縫內的壓力分布與縫內流體的流動有關，壓裂起始于高壓流體誘發的孔壁破裂，但壓裂的最終效果主要取決于此后裂縫的擴展過程，因此，以井底壓力作為縫內壓力會導致計算結果的準確性降低。筆者采用廖新維等人[11]提出的垂直裂縫不穩定滲流數學模型，該模型包括地層中的流體流動和裂縫中的流體流動2 部分。

對于裂縫，其內部流體的流動一般看成一維流動。假設儲層上下為不滲透邊界，裂縫與井筒相對稱，不計裂縫寬度，忽略毛細管壓力和重力的影響，壓裂液為微可壓縮單相流體。建立數學模型，并引入無因次量：

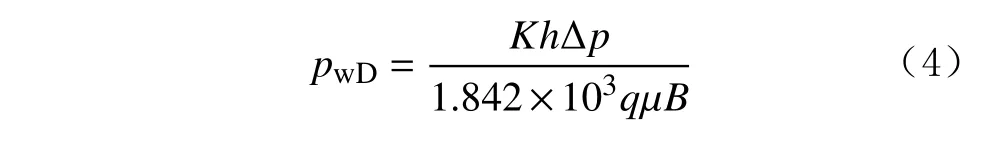
式中：pwD為無因次井底壓力；K 為滲透率，mD；h 為儲層厚度，m；Δp 為壓差，MPa；q 為流量，m3/s；μ 為黏度，mPa·s；B 為體積系數。

利用Laplace 變換方法求解，可以得到：

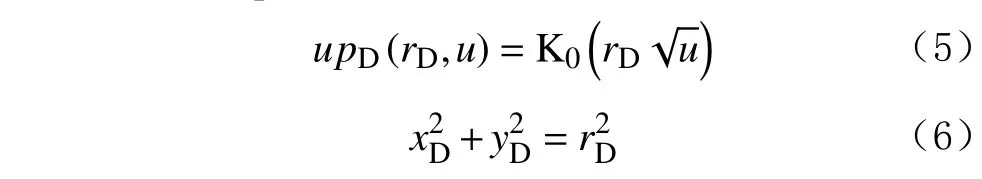
式中：u 為Laplace 變量；pD為無因次地層壓力；rD為無因次裂縫徑向長度；K0為貝塞爾函數；xD，yD分別為x 和y 方向的無因次裂縫長度。

對于裂縫，其內部流體的流動一般看作一維流動。通過壓力疊加原理，可以得到無限導流垂直裂縫在Laplace 空間內的壓力分布表達式：

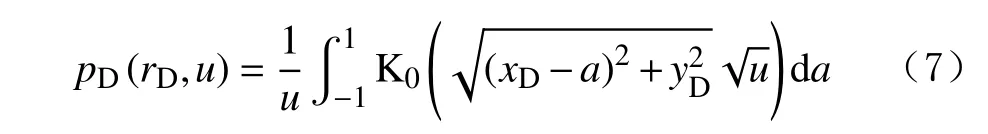
式中：a 為積分變量。

根據式（7）可計算出裂縫內部的壓力，并用于裂縫擴展轉向計算。

1.3 位移不連續法裂縫尖端轉向解析模型

求解靶向壓裂裂縫轉向模型時采用位移不連續法[12-13]，可較為準確地計算裂縫性地層的壓裂裂縫轉向問題。對于裂紋邊界及常規邊界，均以不連續位移為基本解。假設只有縫內壓力在縫端產生奇異性；外部應力場并不直接影響應力強度因子，只是通過改變縫內虛擬力來影響應力強度因子。將這種方法用于域內裂紋、邊裂紋及彎曲裂紋的多裂體分析，可以方便地求得多裂體裂紋的應力強度因子。當裂紋擴展時，只需在新增加的裂紋面上繼續計算即可。

由裂紋作用均布力的應力強度因子公式可以得到縫尖強度因子KI和KII的表達式：

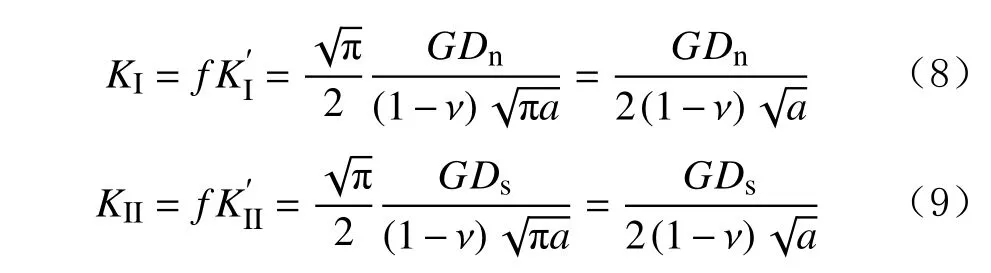
式中： KI、 KII分別為修正后的I、 II型縫尖強度因子；f 為 修 正 系 數；為I 、 II型 初 始 縫 尖 強 度 因 子；G 為剪切模量，GPa；ν 為泊松比；Ds、Dn分別為切向和法向不連續位移，其可用應力σx、σy和τxy表示，MPa。

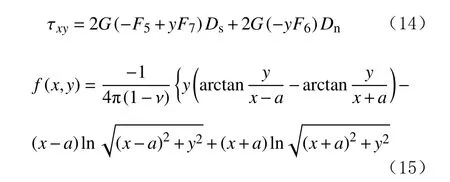
式中：Ux和Uy分別為x 和y 方向的平面應變；F2—F7為函數f 的一階x 偏導數、一階y 偏導數、對x 和y 的二階混合偏導數、對x 和y 的三階（y2）混合偏導數、對y 的三階偏導數。

求解上述方程組，可得到各單元的不連續位移{D}。

因為外部應力場并不直接影響多裂紋體的應力強度因子，因此利用求解的裂紋面上的不連續位移D 可以求出多裂紋體的應力強度因子。

上述用應力表示位移、再用縫端單元位移修正法求應力強度因子的方法，可在保證計算精度的前提下，大幅加快計算速度，提高軟件運算效率。

1.4 靶向壓裂預制縫轉向流固耦合模型

按照實際壓裂施工步驟求解靶向壓裂裂縫轉向模擬解析模型，從井口設置井口壓力、壓裂液的黏度及排量等施工參數，計算得到井底壓力；以此值為壓裂裂縫的縫內壓力初值，無因次化后代入到Laplace 空間中，計算得到縫內壓力與裂縫長度的函數關系，從而得到裂縫每次擴展時的縫尖應力；求得縫尖應力后轉換為Ds和Dn，代入式（8）和式（9）可得裂縫強度因子，據其判斷裂縫是否起裂、轉向。模型計算流程如圖1 所示。

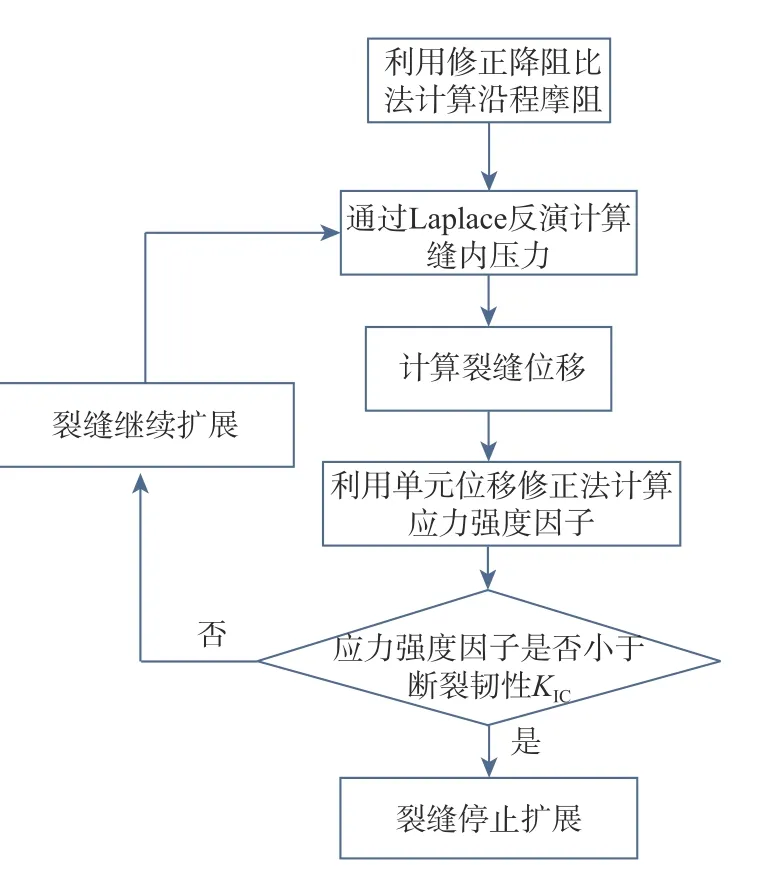
圖 1 模型計算流程Fig. 1 Model calculation process

利用該模型將碳酸鹽巖靶向酸壓過程有機整合為一個整體，通過改變施工參數，可對不同地層進行預制縫靶向壓裂轉向模擬計算。

2 模型準確性驗證

2.1 室內物理模擬準確性測試

采用中國石油大學(北京)巖石力學實驗室自行設計組建的大尺寸真三軸模擬試驗系統，應用規格300 mm×300 mm×300 mm 的巖樣進行模擬試驗，為驗證軟件模擬結果的準確性，制作含有45°預制縫的巖樣，比較試驗值與模擬值的相似度，以驗證軟件模擬的準確程度。設置試驗參數為：σH=14 MPa，σh=11 MPa，排量10 mL/min，液體黏度20 mPa·s。

試驗結果：在含有預制縫的情況下，壓裂裂縫發生轉向現象，轉向距離約為7.40 cm。模擬結果：裂縫起裂后轉向距離為7.31 cm。試驗結果與模擬結果非常接近。試驗還發現，預制縫角度為45°時，人工裂縫轉向結果與軟件模擬結果一致，說明軟件模擬結果比較準確。

2.2 有限元模擬準確性測試

在物理模擬試驗驗證的基礎上，使用擴展有限元進行流固耦合計算，對比2 種模型的差異，模擬參數設置為：彈性模量45 GPa，泊松比0.25，最大水平主應力120 MPa，最小水平主應力90 MPa，預制縫長度1.50 m，壓裂施工排量5 m3/min，壓裂液黏度20 mPa·s。2 種模型的計算結果如圖2 所示。

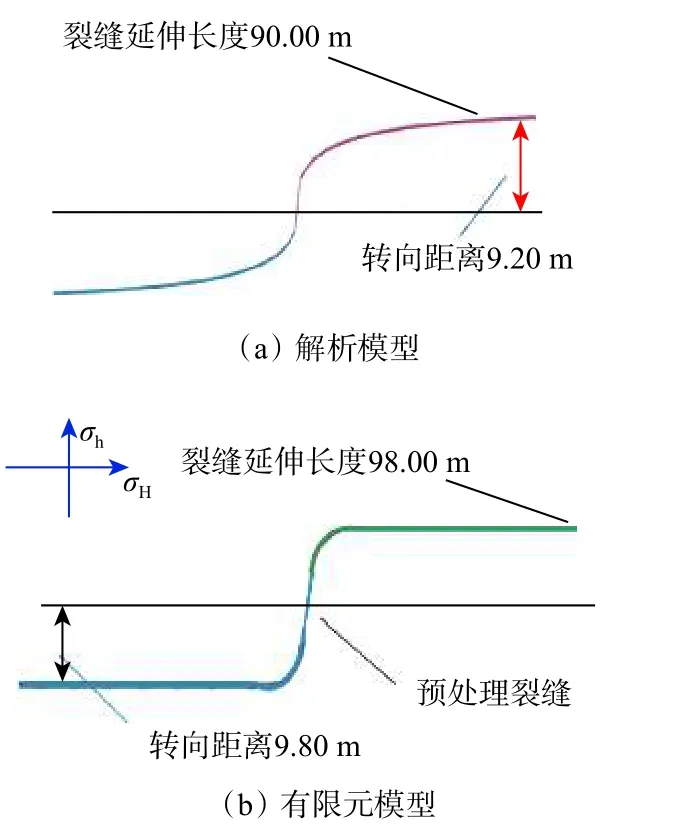
圖 2 2 種模型模擬結果的對比Fig. 2 Comparison on the simulation results of different models

從圖2 可以看出，2 種模型的裂縫擴展轉向結果大致相同，轉向距離誤差6.1%，延伸長度誤差8.2%。區別在于有限元模型對于應力差條件的收斂性過強，導致裂縫在轉向后完全沿垂直于最小水平主應力的方向擴展，而實際壓裂中裂縫擴展趨勢應是逐步轉向、最終與最小水平主應力方向垂直。因此，可以認為解析模型的模擬結果更貼近實際情況，且該模型耦合的因素包括地應力差、地層彈性參數、施工排量、黏度、裂縫滲透率、近井表皮系數和壓裂液濾失性等，較有限元模型考慮的參數更為全面。同時，解析模型的模擬效率更高，使用便捷，運算時間短。

3 轉向范圍影響因素分析

對含有預制縫的人工裂縫起裂擴展形態進行研究，并分析地應力差、彈性模量等因素對裂縫轉向范圍的影響程度。將預處理縫與最大水平主應力方向的垂向距離定義為預處理距離，將裂縫轉向后裂縫尖端與最大水平主應力方向垂向距離定義為裂縫轉向距離。

3.1 壓裂液黏度

采用單一變量法，通過改變壓裂液黏度，分析其對裂縫轉向距離的影響，結果如圖3 所示。

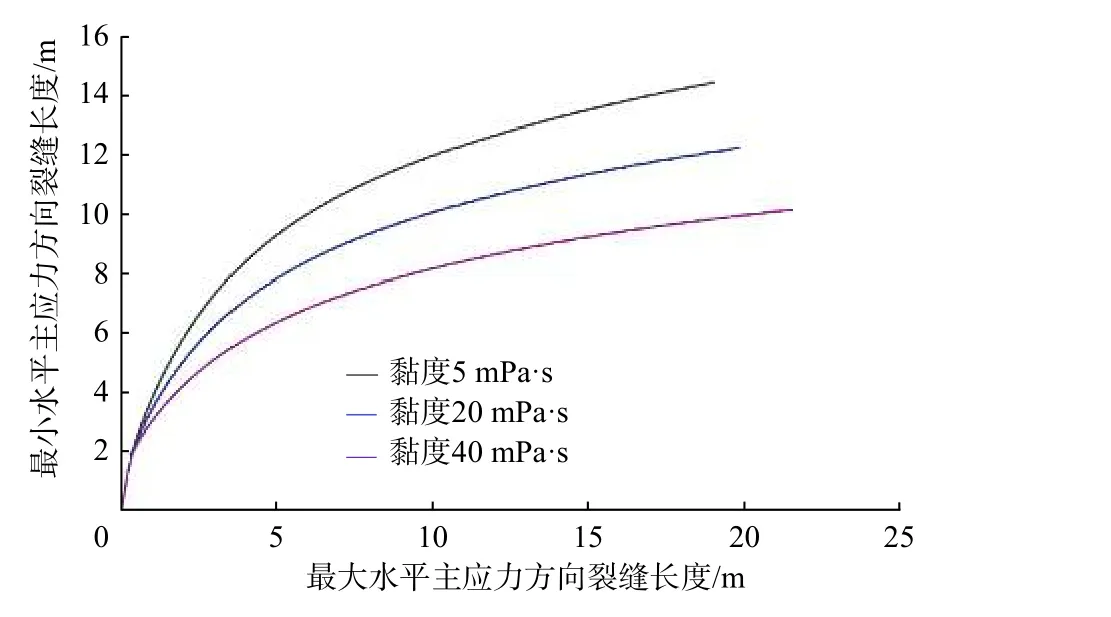
圖 3 不同壓裂液黏度下的裂縫轉向距離Fig. 3 Fracture diverting distances under different fracturing fluid viscosities

從圖3 可知：低黏度的壓裂液可以增大裂縫轉向距離；壓裂液黏度降低，人工裂縫的轉向距離將增大。模擬參數設置為地應力差15 MPa，排量5 m3/min，使用黏度5 mPa·s 壓裂液時的裂縫轉向距離可達到14.00 m，相較于使用黏度40 mPa·s 壓裂液增大近6.00 m。因此，使用滑溜水或者酸液進行預處理，可使靶向壓裂裂縫轉向距離增大。

3.2 施工排量

模擬參數設置為地應力差15 MPa，壓裂液黏度3 mPa·s，通過改變排量，分析其對裂縫轉向距離的影響，結果如圖4 所示。

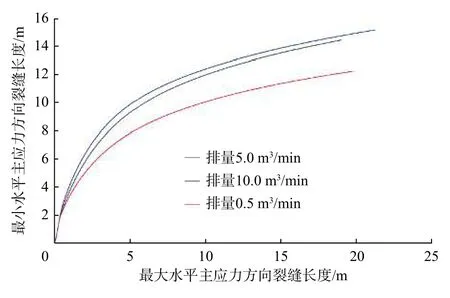
圖 4 不同排量下的裂縫轉向距離Fig. 4 Fracture diverting distances under different flow rates

從圖4 可知，排量對裂縫轉向距離的影響呈非線性關系，提高排量會導致摩阻急劇增大，反而導致裂縫轉向距離減小，因此需要優選排量。施工排量增大，人工裂縫轉向范圍明顯增大，施工排量從0.5 m3/min 增大到5.0 m3/min 時，裂縫轉向距離從13.00 m 增大到16.00 m；但排量增大到10.0 m3/min時，裂縫轉向距離卻是減小的，原因是增大排量會引起摩阻增大，從而影響裂縫轉向距離。由于摩阻的存在，排量需要經過多次模擬優選，才能針對不同工況得到其最優排量。

3.3 預制縫角度

預制縫角度是預處理裂縫與最小水平主應力方向的夾角，也稱起裂方位角。模擬參數設置為地應力差15 MPa，壓裂液黏度5 mPa·s，排量5.0 m3/min，模擬不同起裂方位角下的裂縫轉向距離，結果如圖5所示。

從圖5 可知，起裂方位角減小，裂縫轉向距離增大。起裂方位角減小，人工裂縫轉向距離明顯增大，當前參數下，起裂方位角10°時的裂縫轉向距離為16.00 m，相較起裂方位角30°增大4.00 m。由此可見預處理裂縫與最小水平主應力方向夾角應盡量減小，以得到更大的人工裂縫的轉向距離。

3.4 預處理方式

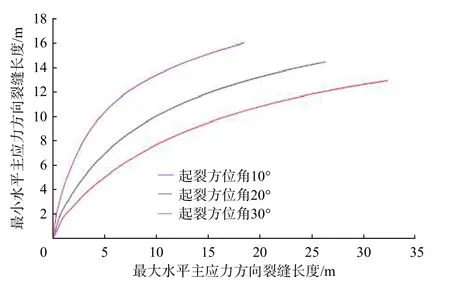
圖 5 不同起裂方位角下的裂縫轉向距離Fig. 5 Fracture diverting distances at different fracture initiating angles

結合多次模擬所得結論，設置當前儲層條件下（應力差20 MPa）最有利于裂縫延伸擴展的施工參數，模擬爆燃壓裂[14]、水力噴射壓裂[15]和射孔壓裂3 種預處理方式下的裂縫擴展轉向范圍，結果見圖6—圖8。其中，爆燃壓裂預制裂縫長度為12.00 m ，水力噴射壓裂預制裂縫長度為2.00 m，射孔壓裂預制裂縫長度為1.00 m。

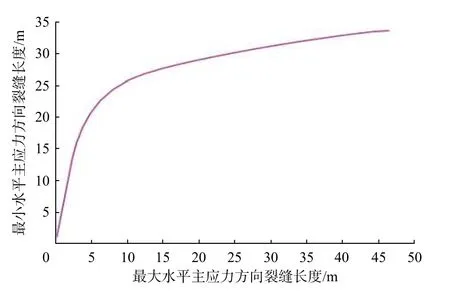
圖 6 爆燃壓裂裂縫轉向距離模擬結果Fig. 6 Simulation results of fracture diverting distance of blasting fracturing

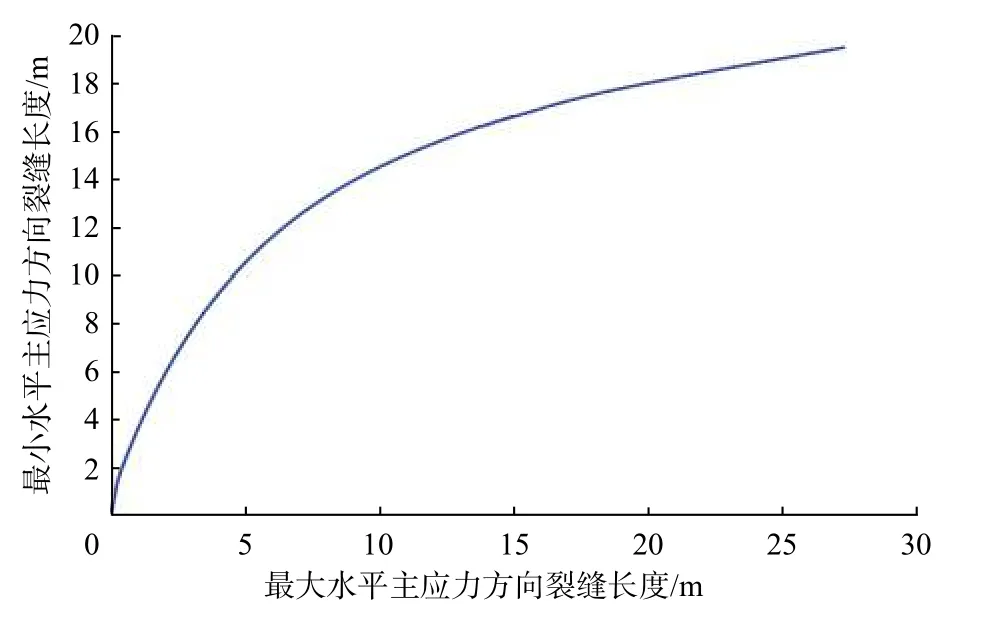
圖 7 水力噴射壓裂裂縫轉向距離模擬結果Fig. 7 Simulation results of fracture diverting distance of hydraulic jet fracturing

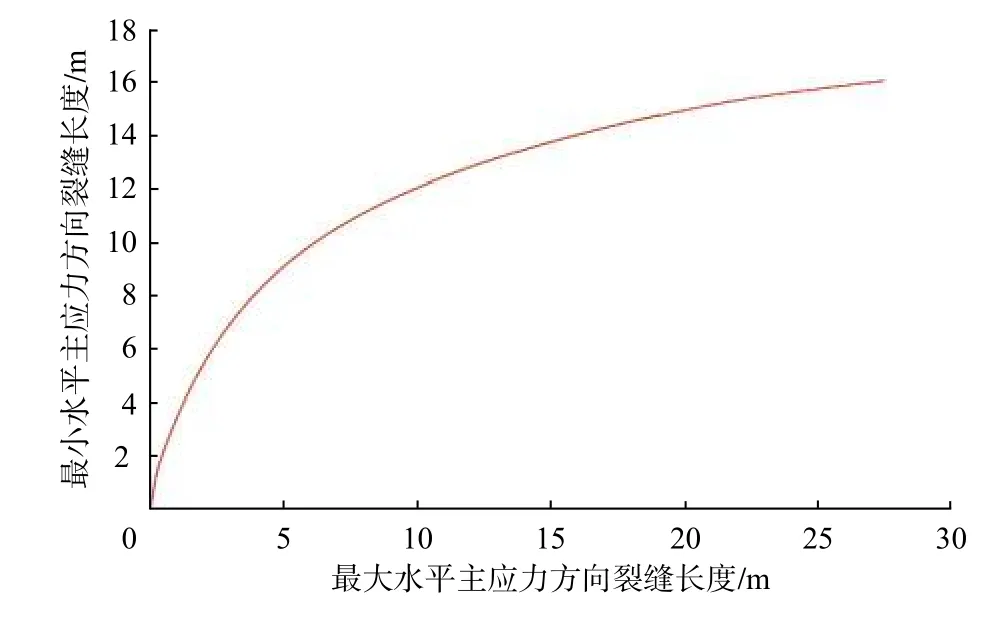
圖 8 射孔壓裂裂縫轉向距離模擬結果Fig. 8 Simulation results of fracture diverting distance of perforating fracturing

從圖6—圖8 可知，3 種預處理方式均具有轉向作用，爆燃壓裂預處理方式下的最大裂縫轉向距離為34.00 m，水力噴射壓裂預處理方式下的最大裂縫轉向距離為19.30 m，射孔壓裂預處理方式下的最大裂縫轉向距離為16.20 m，可見爆燃壓裂預處理方式的裂縫轉向距離和影響范圍最大。

3.5 地應力差

使用單一變量法，模型參數設置為預處理縫長1.50 m，預處理角度10°，壓裂液黏度5 mPa·s，排量5.0 m3/min，地應力差分別設置為15，25 和40 MPa。模擬不同地應力差下的裂縫轉向距離，結果見圖9。

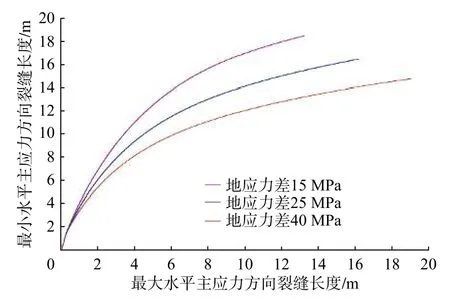
圖 9 不同應力差下的裂縫轉向距離Fig. 9 Fracture diverting distances under different stress differences

從圖9 可知，地應力差對裂縫轉向距離影響較大，地應力差越大，裂縫延伸限制程度越大，裂縫轉向距離越小。地應力差為15 MPa 時，裂縫轉向距離為20.00 m；應力差25 MPa 時，裂縫轉向距離為15.00 m；應力差為40 MPa 時，裂縫轉向距離僅為9.50 m；應力差提高25 MPa，裂縫轉向距離減小10.50 m。

3.6 泊松比

使用單一變量法，模型參數設置為：預處理縫長1.00 m，預處理角度10°，壓裂液黏度5 mPa·s，排量5 m3/min，地應力差15 MPa，泊松比分別設置為0.25，0.40 和0.55。模擬不同泊松比下的裂縫轉向距離，結果見圖10。

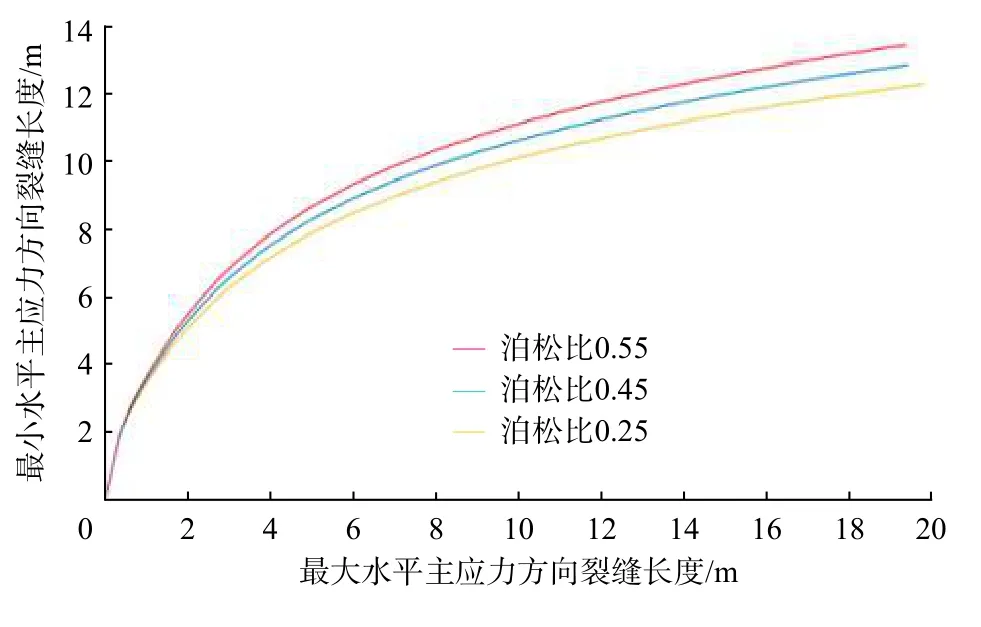
圖 10 不同泊松比下的裂縫轉向距離Fig. 10 Fracture diverting distances under different Poisson′s ratios

由圖10 可知：泊松比對裂縫轉向距離影響較小；泊松比增大，裂縫轉向距離小幅增大。

3.7 彈性模量

模型中參數設置為預處理縫長10.00 m，預處理角度5°，壓裂液黏度5 mPa·s，排量5.0 m3/min，地應力差20 MPa，彈性模量分別設置為45 和60 GPa。模擬不同彈性模量下的裂縫轉向距離，結果見圖11。

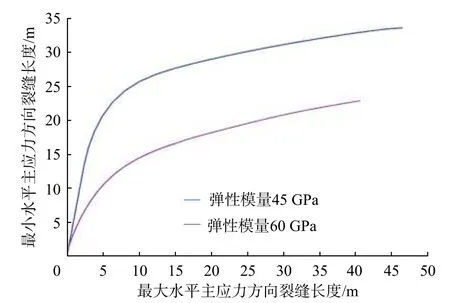
圖 11 不同彈性模量下的裂縫轉向距離Fig. 11 Fracture diverting distances under different elastic modulus

由圖11 可知，儲層巖石的彈性模量越小，人工裂縫的轉向距離越大。彈性模量45 GPa 的地層較60 GPa 的地層裂縫轉向距離增大15.00 m。

以上研究表明，對于含預制縫的人工裂縫，預制縫長度對轉向范圍影響最為顯著，預制縫長度越長，人工裂縫轉向距離越大；彈性模量、地應力差、壓裂液黏度、施工排量和起裂方位角對人工裂縫轉向距離影響程度相近，泊松比對轉向距離的影響最小。

4 結論與建議

1）對管柱沿程摩阻和裂縫縫內壓力衰減進行耦合，并使用位移不連續法，建立了碳酸鹽巖壓裂施工一體化裂縫擴展模型，形成了預制縫轉向溝通影響因素的評價方法。

2）碳酸鹽巖壓裂施工中預制縫縫長與起裂方位角對裂縫轉向距離的影響較大，壓裂設計初期應在明確地層巖石力學參數、地應力等情況后首先確定預制縫參數，再對排量、黏度等其他施工參數進行設計。

3）塔河油田碳酸鹽巖儲層預制縫壓裂施工時，預制縫起裂角度越小，預制縫越長，靶向壓裂裂縫的轉向距離越大，擴展距離越長。優化施工排量時應考慮管柱沿程摩阻；壓裂液黏度越小，壓裂裂縫的轉向距離越大。

4）應積極探索建立碳酸鹽巖三維壓裂裂縫擴展模型，后續研究還需要突破模型假設地層均質的局限性，更加貼近地層實際情況，并深入研究多因素共同作用時對人工裂縫轉向距離的影響。