另辟蹊徑，解絕對值不等式

喻敏

（重慶市涪陵第一職業中學校，重慶 408100）

不等式是中學數學中的主要內容之一，很多章節的學習都要用到不等式的有關知識，其中不等式的解法是重點，而含絕對值的不等式的解法是難點之一。下面我就解含絕對值的不等式的解法談點粗淺的看法。

眾所周知，解絕對值不等式的基本思想，就是設法去掉絕對值符號，把不等式轉化為不含絕對值的不等式進行求解，即將未知的知識轉化為已知的知識，而化歸思想也是我們認識新事物，研究新問題的重要方法之一。

去掉絕對值符號的方法主要有公式法、平方法等。而公式法是最基礎的方法，其原理是將絕對值不等式轉化為一元一次不等式進行求解。平方法則是將絕對值不等式進行兩邊平方，然后進行求解。在這里,我以例題向大家介紹一種敝人認為更簡便的解絕對值不等式的方法——“八字口訣”法：變形、解方程、用口訣。

一、“八字口訣”解絕對值不等式的由來

教材上是這樣來推導出絕對值不等式的解集的：

第一步：復習絕對值的幾何意義

第二步：│x│=3的幾何意義：數軸上到原點的距離等于3的所有點構成的集合。利用圖形求出解為3和-3。

第三步：由│x│＜3的幾何意義：數軸上到原點的距離小于3的所有點構成的集合得出解集為。

由│x│＞3的幾何意義：數軸上到原點的距離大于3的所有點構成的集合得出不等式的解集為。

第四步：由│x│＜3和│x│＞3的解集，得出│x│＜a和│x│＞a（a＞0）的幾何意義和解集，從而得出解不等式│x│＜a和│x│＞a（a＞0）的口訣：大于取兩邊，小于取中間。。

我對以上內容的理解為：形如│x│＜a或│x│＞a的解題關鍵是找出兩個關鍵點（即，絕對等于a的兩個數），然后再利用一元二次不等式的一個訣竅（大于取兩根之外，小于取兩根之內）寫出不等式的解集。然后我將此類不等式的解法歸納為以下八個字：①變形（變形為│x│＜a或│x│＞a(a＞0)的形式），②解方程（│x│=a），③用口（利用口訣“大于取兩根之外，小于取兩根之內”寫出絕對值不等式的解集）。現在就讓我們一起來驗證“八字口訣”的準確性。

二、用“八字口訣”解形如│x│＜a或│x│＞a(a＞0)的不等式

分析：法1：（1）題目中的形式和基本形式不同，故而要先變形為

（2）利用“大于取兩邊，小于取中間”寫出不等式的解集。

（3）由于變形后的不等號為大于，故而此不等式的解集應該取兩根之外，通過數形結合可以得出不等式的解集。

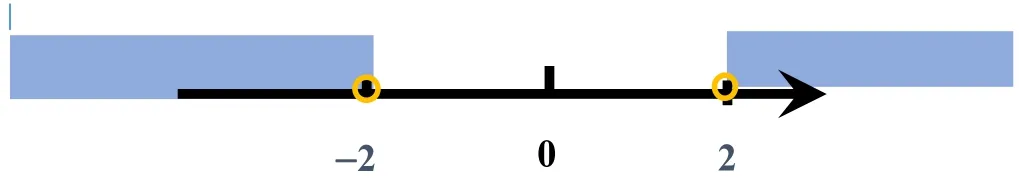
∴利用“口訣”：大于取兩根之外，小于取兩根之內求出不等式的解集為

注意：（1）根據不等式的符號確定解集時，一定是根據變形后的不等式的符號。

（2）由例題可以看出，“八字口訣”和公式法解絕對值不等式得出的解集一樣，這說明“八字口訣”是正確的。

（3）由于變形后的不等號為小于，故而此不等式的解集應該取兩根之內，通過數形結合可以得出不等式的解集。

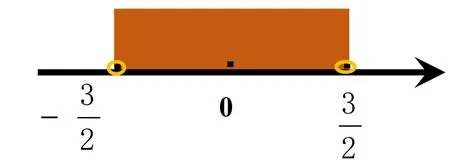
小結：由上面兩個例題可以看出，“八字口訣”是可以用來解形如│x│＜a或│x│＞a(a＞0)的不等式的。下面我將接著用“八字口訣”解形如ax的不等式。

三、利用“八字口訣”解形如或（c＞0）的不等式

區別：絕對值里面的式子不同

聯系：都是絕對值的不等式，形式相同。

（2）我們只需將2x+1看成一個整體m，那么形式就完全與相同了，即可利用“大于取兩根之外，小于取兩根之內”的口訣求出m的范圍，然后再解方程2x+1=m就可以求出原不等式的解集了。

解：法1：令，則不等式變形為，即

現將m換成2x+1，可得

根據“口訣”：大于取兩根之外，小于取兩根之內可得不等式的解集為

四、利用“八字口訣”解形如的不等式

分析：此題看似比較復雜，學生一開始可能無從下手。現在我們可以將此題看成兩個絕對值不等式和組成不等式組，然后再求不等式組解集即可。這就將未知的知識轉化為我們已經學過的知識，從而降低了解題難度，所以解題關鍵在于將未知轉化為已知。

2x-3＜5②

法1：設2x-3=m，則原不等式組化為m＞1③

m＜5④

解不等式③得m＜-1或m＞1 ⑤

解不等式④得-5＜m＜5⑥

將2x-3=m代入⑤得x＜1或x＞2；代入⑥得-1＜x＜4所以原不等式的解集為{x-1＜x＜1或2＜x＜4}

法2：令2x-3=1，解方程得x1=1,x2=2

即不等式①的解集為{xx＜1或x＞2}

令2x-3=5，解方程得x1=-1,x2=4，

即不等式②的解集為{x-1＜x＜4}

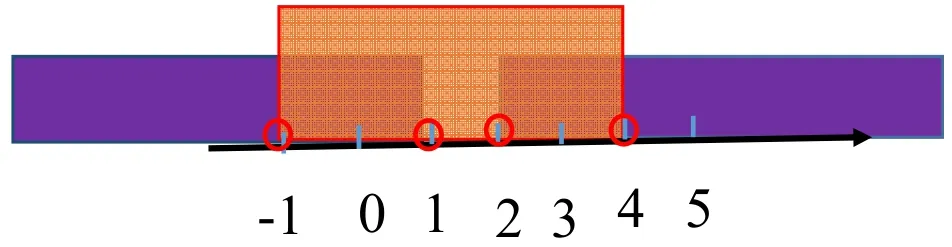
小結：由此可見，“八字口訣”仍然于解形如的不等式。

綜上所述，“八字口訣”對于一般的絕對值不等式都適用。此方法將解一元二次不等式的方法（解方程，大于取兩根之外，小于取兩根之內）用到了解絕對值不等式之中，有效的將未知知識用已知的知識來解答，而且通過解答例題證明：此方法解形如和形如比教材上介紹的方法更簡單、更準確。以上皆是本人個人觀點，如有不對、不足的地方還請大家批評指正。