妙用圓巧解線段最值問題

江蘇省鎮江科技新城實驗學校 趙妍珊

該類問題看似是與圓無關的幾何最值問題，但是可以運用圓的定義找出圓的模型。因此該類問題的關鍵就變成了找動點的運動軌跡，使得問題雖然沒有圓出現，但是卻勝過有圓，以此運用構造法構造出圓，從而提升學生的解題能力。

一、定長定點找圓

根據教材對圓的定義可知，平面上到定點的距離等于定長的所有點組成的圖形叫作圓。根據上述定義，只要能夠找到某一動點在移動時與同一定點的距離相等，即找出了以定點為圓心，以定長為半徑的圓，再利用圓外一點和圓上一點的距離求出最值問題。

例1：如圖1，在邊長為2 的菱形ABCD中，∠A=60°，M是AD邊的中點，N是AB邊上的動點，將△AMN沿MN所在直線翻折得△A'MN，連接A'C，則A'C長度的最小值為多少？

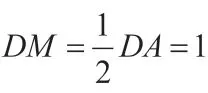
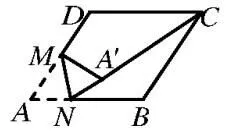
圖1

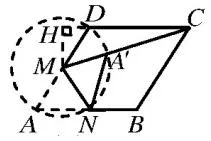
圖2

反思：上述例題看似很復雜無處下手，但是仔細審視題目可以發現動點N與不動點M之間的長度為定值，由此根據圓的定義得到“隱形圓”，在確定圓的圓心和半徑后，就可以根據所求問題適時作輔助線。因此學生在面對該類問題時可以首先考慮題目中是否有隱含條件，如果有就可以在途中作出來，再觀察題目求解線段的最值。

二、定弦定角找圓

在求解線段最值問題時，往往會出現多個動點的情況，如果此時兩個動點同時考慮，學生會出現思維混亂、考慮不全面或者出現重復的情況，因此該類問題在考慮時可以“定一動一”，或略過題目本身的多動點而重新確定動點輔助解題。

例2：如圖3，E、F是正方形ABCD的邊AD上的兩個動點，滿足AE=DF。連接CF交BD于點G，連接BE交AG于點H。若正方形的邊長為2，則線段DH長度的最小值多少？

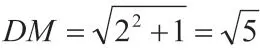
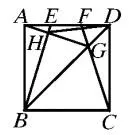
圖3

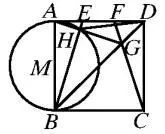
圖4

反思：上述例題雖然也沒有提到圓，且存在多個動點，如果直接從兩動點出發，很顯然無形中增加了該題的難度，但是如果在求解時可以忽略兩動點，重新確定動點的方法找出隱形圓，那么該題就迎刃而解了。因此學生在求解多動點問題時可以考慮另辟蹊徑，重新確定動點來求解。

三、運用旋轉軌跡找圓

旋轉是幾何體中常遇到的變換方式，而大部分同學對于該種變換理解不清，學生在解題之前應明確旋轉所帶來的等量關系，包括線段相等、角度對應、面積不變等關系，而這些都是接下來解題的關鍵。其次，旋轉必然存在旋轉角度、旋轉軌跡，多數情況下旋轉軌跡為弧，而弧是圓的一部分，因此學生在解決該類問題時可以優先考慮找“隱形圓”。

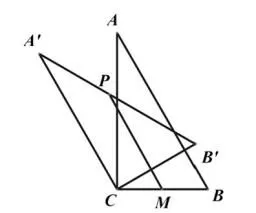
圖5

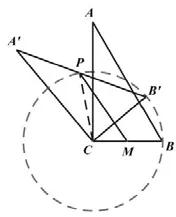
圖6

例3：如圖5，在Rt △ABC中，∠ACB=90°，將△ABC繞定點C逆時針旋轉得△A'B'C，M是BC的中點，P是A'B'的中點，連接PM,若BC=2，∠BAC=30°。求線段PM的最小值和最大值。

解 析： 由 題 可 得AB=A'B'=4， 點P為A'B' 的 中 點， 則CP=CB=2,即可得以點C為圓心，以CB為半徑的圓，圓內一點到圓上各點的連線中,點與過圓心的直線與圓近交點距離最短,遠交點距離最長。根據圓內一點與圓上點間的關系可得點P與點M間的距離關系有三種可能，如圖7 所示，故線段PM的最小值為MP=CPCM=1，線段PM的最小值為MP=CM+CP=1+2=3。

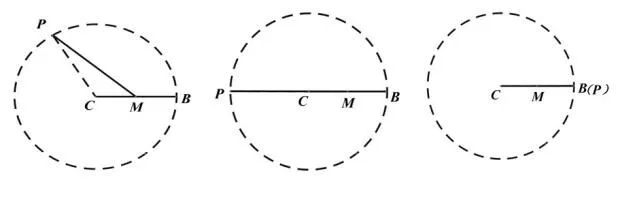
圖7

反思：該類問題中，學生需要理解清題意，明確圖形變換方式以及導致的變與不變，理清這些后方能找出關系，明確解題思路。旋轉帶來的弧是圓的一部分，因此可以考慮將這個旋轉弧“擴展”為圓，為接下來的解題提供思路。

綜上所述，“隱形圓”普遍運用于線段最值問題中，而一旦找到了“隱形圓”，問題也就迎刃而解。因此，學生在面對該類問題時首先應確定變量、定量、線段間的對應關系等，并由此觀察思考半徑與圓心的可能存在形式，就此確定圓的位置，解決問題。