利用神經網絡識別高分子鏈在表面的吸附相變*

孫立望 李洪 汪鵬君? 高和蓓 羅孟波

1) (溫州大學數理與電子信息工程學院,溫州 325035)

2) (溫州職業技術學院信息系,溫州 325035)

3) (浙江大學物理系,杭州 310027)

采用深度神經網絡和Monte Carlo (MC)模擬方法研究了線性高分子鏈在均質表面以及條紋表面的臨界吸附現象.通過MC模擬退火算法構建高分子鏈的構象樣本集,采用狀態標記法和溫度標記法對模擬產生的樣本集進行標記并采用神經網絡對標記后的樣本進行訓練,發現神經網絡可以很好地識別高分子鏈在均質表面的脫附態和吸附態以及在條紋表面的脫附、多條紋吸附和單條紋吸附的三個不同狀態,且發現神經網絡對這兩種樣本標記法得到一致的臨界吸附溫度.通過對訓練集大小與神經網絡的識別率之間的關系進行研究,發現神經網絡可以在每個溫度抽取較少的訓練樣本集上學習得到較高的高分子鏈構象狀態的識別率.神經網絡結合傳統MC方法可以為高分子模擬計算研究提供一種新的方法.

1 引 言

近年來,機器學習在各個領域都受到了研究人員的廣泛關注[1-5],作為機器學習的分支,人工神經網絡憑借著出色的模式識別能力活躍在圖像識別[6-8]、語音識別[9,10]、自然語言處理[11,12]以及推薦系統[12,13]等領域.更有學者認為,人工神經網絡[14-16]會成為最有可能實現人工智能的方法之一.神經網絡采用反向傳播(back propagation,BP)算法[17,18],并使用大量的樣本進行訓練,在模式識別問題上可以達到很高的準確率.例如在比較經典的MNIST手寫數字識別問題和ImageNet圖像分類問題上,采用全連接神經網絡和卷積神經網絡分別取得了99.17%[6]和96.43%[7]的識別率.

最近,人工神經網絡被用于凝聚態物理、高分子物理等領域研究.卷積神經網絡被用來區分凝聚態物質在高溫下的順磁性和在低溫下的鐵磁性[2],還有深度學習被用來研究聚合物的Coil-globule相變,這種將機器學習與MC方法相結合的方法在科學計算研究上取得了非常好的效果[1].這激發我們將機器學習應用于高分子吸附的研究,也為我們研究的可行性提供了保障.對于高分子鏈在表面的吸附相變問題已經有研究人員采用傳統的MC模擬方法進行了研究并且計算了臨界吸附點[19-25].本文將神經網絡和MC模擬方法相結合來研究高分子鏈在表面的吸附相變.吸附表面分為均質表面和條紋表面兩種情況.研究表明對于單一的高分子鏈,神經網絡可以很好地識別在均質表面的脫附態和吸附態以及在條紋表面的脫附態、多條紋吸附態和單條紋吸附態,并分別計算出了高分子鏈在均質表面以及條紋表面的臨界相變溫度,為研究高分子鏈的臨界吸附提供了一種新方法.

2 模型與方法

MC模擬方法在高分子模擬領域是非常經典的研究方法之一,本文采用MC模擬生成樣本.高分子鏈是基于自回避行走算法(self-avoiding walking,S AW)生成的,鏈長N=160,鍵長取值為模擬空間采用三維簡立方格子空間,在Z=0以及Z=D處分別設置一個不可穿透的擋板,D＞Nν(ν 為三維的Flory指數,ν=0.588),Z=0處的表面會對單體產生吸附作用,Z=D處的表面對單體只考慮體積排斥作用,目的是使高分子鏈不遠離具有吸附作用的表面.在X和Y兩個方向設置周期性邊界條件,模擬盒的水平方向尺寸LX=LY＞Nν(ν 二維的Flory指數,ν=0.75),在條紋寬度L=4的條紋表面上,為了條紋滿足周期性條件,統一取較大模擬盒尺寸 LX=LY=144.采用了模擬退火算法,設置了48個溫度用于退火,在每個溫度都將經歷 T=2.5×N2.13MCS來到達平衡狀態.采用Metropolis重要性抽樣方法[26,27]用來判斷高分子鏈的每一步運動是否被接受.假設每一個單體接觸到吸附表面就獲得一個能量?=-1,然后以概率p來判斷該運動是否被接受,其中

這里的 ΔE 表示每一次運動前后的能量變化,kB為玻爾茲曼常數,T為溫度.

本文采用卷積神經網絡和全連接神經網絡研究高分子鏈的吸附相變,在每個溫度下抽取了9600個樣本用于神經網絡的訓練和測試.神經網絡的梯度更新采用累積更新算法,并使用滑動平均以及正則化來防止過擬合.本文所采用的神經網絡模型如圖1所示.

在圖像識別領域通常將一張圖片轉換成矩陣輸入神經網絡.卷積神經網絡的結構示意圖如圖1(a)所示.將構象的坐標信息當作“RGB圖像”轉換成 16×10×3 的三維矩陣數據輸入卷積神經網絡,通過卷積層提取特征、池化層泛化特征、全連接層組合特征以及丟棄(dropout)層暫時丟棄部分神經元和連接來防止過擬合,最后輸出高分子構象狀態的識別結果.全連接神經網絡的結構示意圖如圖1(b)所示.將坐標數據直接拉伸成長度為480的一維數據,經過若干隱藏層提取特征最后輸出高分子構象狀態識別結果.在全連接網絡中dropout也通過隨機丟掉一些神經元和連接來防止過擬合,正則化(regularization)可以通過對學習到的權重加上懲罰項來防止過擬合,如L2正則化.

圖1 神經網絡結構示意圖 (a) 卷積神經網絡,INPUT表示輸入層,Convolution表示卷積層,MAXPOOL表示池化層,Full connection表示全連接層,OUTPUT表示輸出層,PADDING方式均為SAME; (b) 全連接網絡的一般結構,其中hidden layer表示隱藏層,使用正則化和dropout來防止過擬合,DIM表示輸入張量的維度Fig.1.Schematic diagram of the neural network structure：(a) Convolutional neural network,INPUT is the data entry,OUTPUT is the learning result,and the padding way is SAME; (b) the general structure of a full-connected network,where regularization and dropout are used to prevent overfitting,and DIM represents the dimension of the tensor.

本文采用ROC (receiver operating characteristic)曲線[28,29]來輔助判斷識別的性能,當ROC曲線圍成的面積越接近1時則說明分類器的性能越好,即采用ROC下面積AUC (area under curve)來判斷分類器的性能,AUC的計算過程為

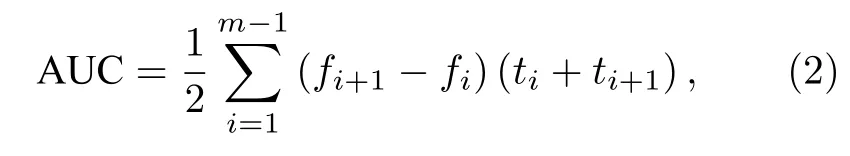
其中f表示假正例率,t表示真正例率,通過將分類器學習的可能性先排序然后將閾值從1開始不斷減小來得到近似的f與t,最后通過近似介值定理計算得到近似的AUC值.正確率則是學習得到的與標記一致的結果所占的比例,如(3)式所示：

其中 N+表示預測正確的樣例個數,N表示總樣例個數.

采用狀態標記法和溫度標記法來對模擬得到的樣本進行標記.狀態標記法針對每一個樣本都進行標記,高分子鏈在每個溫度運行T=2.5×N2.13MCS后,每隔1000 MCS進行一次抽樣,如果這1000 MCS內一直有單體接觸表面,標記為吸附態,否則標記為脫附態.在條紋表面的高分子鏈樣本狀態使用類似的方法.溫度標記法則是首先根據吸附率分布來估計高分子鏈狀態的大致溫度范圍,然后將這段溫度范圍內的樣本都標記為同一個狀態.我們在數據集中選取特定比例的樣本用于訓練,其余的樣本用于測試與驗證.

3 結果與討論

首先采用機器學習研究了均質表面上高分子鏈吸附相變的問題.由前人的研究可知高分子鏈在均質表面存在著高溫時的脫附狀態(desorption state,DE態)、低溫時吸附狀態(adsorption state,AD態)以及在這兩個狀態之間存在的一個臨界相變點.高分子鏈在表面上的吸附率以及構象如圖2所示.

從圖2可以看出當吸附率等于0 (即沒有單體接觸表面)時即為脫附狀態,其典型的構象如圖2(b)所示.當吸附率非零時即發生了吸附現象,稱為吸附狀態,典型構象如圖2(a)所示.臨界相變點大約在 T=1.6 附近,因此對于溫度標記法,我們選取 T∈[1.1,1.4]的樣本作為吸附態標記,T∈[1.8,3.0]的樣本作為脫附態標記.然后采用卷積網絡和全連接網絡來對標記好的樣本進行訓練以及識別,其中全連接網絡采用不同數量的隱藏層來進行實驗,結果如圖3所示.

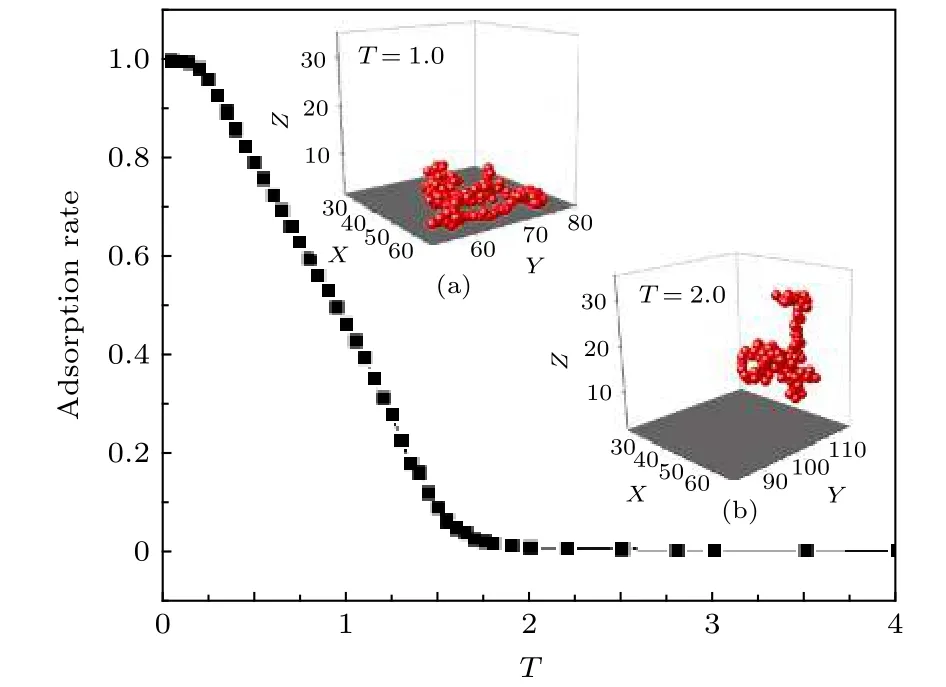
圖2 吸附率與溫度之間的關系.其中鏈長N=160,插圖(a) 是溫度T=1.0時的吸附態構象,插圖(b) 是溫度T=2.0時的脫附態構象Fig.2.Relationship between adsorption rate and temperature.Wherein the chain length N=160,inset (a) is the conformation of polymer adsorbed on the surface at temperature T=1.0,and inset (b) is the conformation of polymer desorbed from surface at temperature T=2.0.

從圖3(a)中可以看出,隨著隱藏層數目的增加,識別率先提高然后趨于穩定,當隱藏層數目大于等于3時識別率基本穩定在97.1%,因此本文缺省所采用的隱藏層數均為3.當Epoch＞30時訓練基本趨于穩定.從圖3(b)中可以看出,即使每個溫度下抽取用于訓練神經網絡的樣本數目(sample per temperature,SPT)足夠小,例如SPT=1時神經網絡仍然擁有91.88%的識別率,也足以識別大部分的樣本.當 SPT≥24 時識別率達到95.5%以上,這說明本文采用較小的樣本數就可以達到較高的高分子構象的識別率.然后我們采用卷積神經網絡進行研究,識別結果如圖4所示.

從圖4可以看出,卷積神經網絡和全連接神經網絡都得到了較高的識別率以及較大的AUC值,因此神經網絡可以較好地識別高分子鏈在均質表面的兩個狀態,且卷積神經網絡的識別率稍高一些.兩種方法都可以用來確定其吸附相變點,且得到的臨界相變溫度相同,均為 TC=1.5 ,稍小于無限鏈長的臨界相變溫度 TC=1.625[19],存在這個差值是因為存在有限尺寸效應,本實驗的高分子鏈長為N=160,隨著鏈長的增加,其臨界吸附溫度會趨于無限鏈長的臨界吸附溫度.

圖3 識別率與訓練樣本的Epoch,神經網絡層數以及每個溫度采用的訓練樣本數之間的關系 (a) 識別率與Epoch的關系圖,SPT (sample per temperature)表示在每個溫度下抽取的用于訓練神經網絡的樣本數目,采用狀態標記法標記樣本.其中nh=1表示隱藏層數目為1,其他的類似,nh=1至 nh=3均采用SPT=192的樣本用于訓練,剩余的樣本用于測試與驗證,插圖描述的是識別率與隱藏層數目nh的關系,該識別率為每個學習器最終穩定的識別結果; (b) 識別率與每個溫度采用訓練樣本數目的關系圖,采用狀態標記法標記樣本,隱藏層數等于3,縱坐標為不同訓練樣本在足夠Epoch下達到穩定時的識別率,測試集均為SPT=7680,且與訓練集不重復Fig.3.The relationship between the recognition rate and the Epochs of training case,the number of neural network layers and the number of training samples obtained from each temperature：(a) the plot of recognition rate versus Epochs.SPT (sample per temperature) represents the number of samples extracted at each temperature for training the neural network.The sample is labeled by status.Where nh=1 indicates that the number of hidden layers is equal to 1,and the others are similar.All of nh=1 to 3 uses a sample of SPT=192 for training,and the remaining samples are used for verification.The illustration depicts the relationship between the recognition rate and the number of hidden layers,which is the final stable recognition result for each classifier; (b) the plot of the recognition rate versus the number of training samples selected at each temperature.The sample is marked by status and the number of hidden layers is equal to 3.The y-axis is the stable recognition rate of different number of training samples under a sufficiently large Epoch.The validation set is SPT=7680 and is not repeated with the training set.

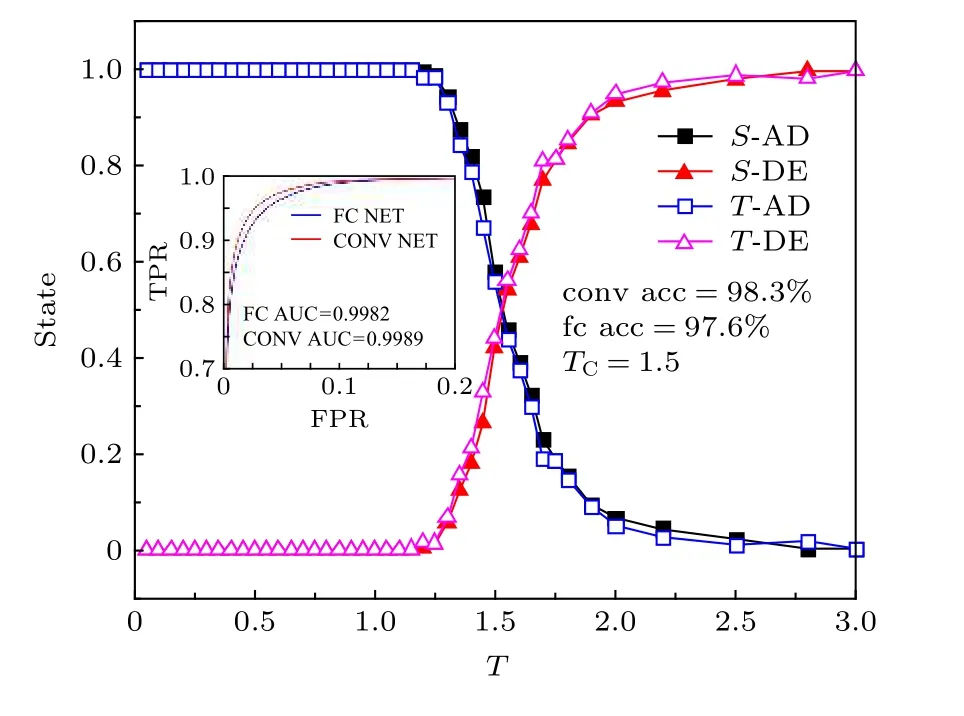
圖4 神經網絡訓練的識別結果圖.橫坐標為溫度,State表示每個溫度下的樣本被識別為某個狀態的概率,S表示狀態標記法,T表示溫度標記法,AD表示吸附態,DE表示脫附態.圖為兩種標記方法的識別結果,卷積網絡的識別率為98.3%,AUC值為0.9989,全連接網絡為97.6%,AUC值為0.9982,兩種標記方法的臨界相變溫度TC=1.5Fig.4.A plot of the result based on the neural network.The x-axis is the temperature,State represents the probability that the sample at each temperature is recognized as a certain state,The letter S represents the state labeling method,the letter T represents the temperature labeling method,AD represents the adsorption state,and DE represents the desorption state.The figure shows the learning results of the two labeling methods.The recognition rate of the convolutional network is 98.3%,the AUC value is 0.9989,the fully connected network is 97.6%,the AUC value is 0.9982,and the critical phase transition temperature is 1.5 of the two labeling methods.

接下來采用神經網絡對高分子鏈在條紋表面的吸附狀態識別進行研究.高分子鏈在條紋表面的吸附率如圖5所示,插圖分別是三種狀態下的典型構象,其中表面上的兩種不同條紋對高分子單體有不同的吸附作用,顏色深的條紋對高分子單體有吸附作用,白色條紋對高分子單體只有體積排斥作用.高分子鏈在條紋表面的構象涉及三種狀態,單條紋吸附態(single-stripe adsorption state)、多條紋吸附態(multi-stripe adsorption state)以及脫附態(desorption state),因此三種狀態之間的轉變伴隨著兩個臨界相變點.

從圖5可以看出,在高溫時高分子鏈的吸附率幾乎為0,即為脫附態,該狀態與均質表面的脫附態相一致; 在低溫時高分子鏈吸附率非常高,而且高分子鏈被單條紋所吸附,我們把這個吸附狀態稱為單條紋吸附態,如圖5(a)所示; 而在中間溫度存在高分子鏈吸附在多條紋上,其吸附率也介于脫附態和單條紋吸附之間,我們把這個吸附態稱為多條紋吸附態.在多條紋吸附態,高分子鏈分布在不同的吸附條紋上,如圖5(b)所示.對于溫度標記法,我們選取 T∈[1.35,1.5]的樣本作為脫附態標記,T∈[0.75,0.9]的樣本作為多條紋吸附態標記,T∈[0.25,0.4]的樣本作為單條紋吸附態標記.然后我們對在條紋表面上的高分子鏈構象樣本進行了訓練與識別,結果如圖6所示.

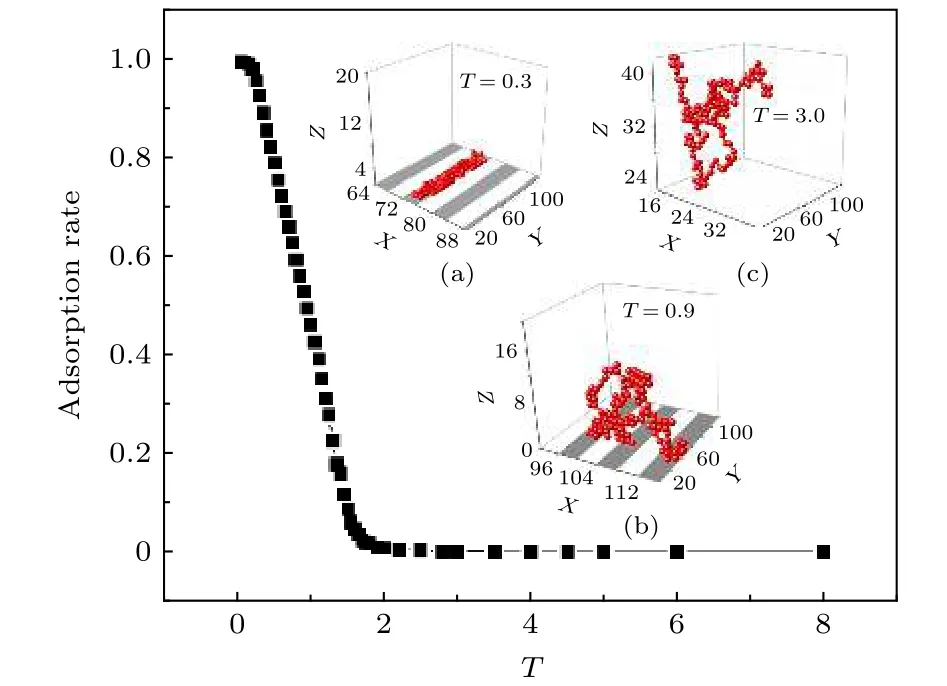
圖5 高分子鏈在條紋表面的吸附率隨溫度的變化以及典型的三態構象示意圖 (a) 單條紋吸附狀態,溫度T=0.3; (b) 多條紋吸附狀態,T=0.9; (c) 脫附狀態,T=3.0.其中鏈長N=160,條紋寬度L=4,條紋方向垂直于x軸,沿著y軸方向延伸,選取的空間尺寸為 25×120×20 ,在條紋表面上,深色部分為吸附條紋,白色部分為作用力排斥條紋Fig.5.The schematic diagram of the adsorption rate of polymer adsorbed on the stripe surface changes with temperature and typical tri-state conformations：(a) the singlestrip adsorption state,where the temperature is 0.3; (b) the multi-strip adsorption state,where the temperature is 0.9;(c) the desorption state,where the temperature is 3.0.Wherein the chain length N is 160,and the stripe width L of the adsorption surface is 4.The stripe direction is perpendicular to the x axis and extends along the y axis,and the selected space size is 25×120×20.For the adsorption surface,the dark part is the adsorption surface and the white part is the non-force surface.

從圖6可以看出,卷積網絡和全連接網絡同樣具有較高的高分子構象狀態的識別率,且AUC值非常接近1,這說明神經網絡可以識別高分子鏈在條紋表面的三種狀態,且卷積神經網絡識別率略高于全連接網絡.兩種樣本標記方法所得到的臨界相變溫度基本相同,其中多條紋吸附向單條紋吸附的相變點為 T1=0.55 ,脫附態向高分子多條紋吸附的相變點為 T2=1.1 ,與文獻[30]計算得到的臨界相變溫度 T1=0.58 和 T2=1.05 相一致.

完成了上述實驗之后,我們發現條紋的表面的高分子識別率要低于均質表面,因此我們對識別過程中的誤判進行了統計,如圖7所示.

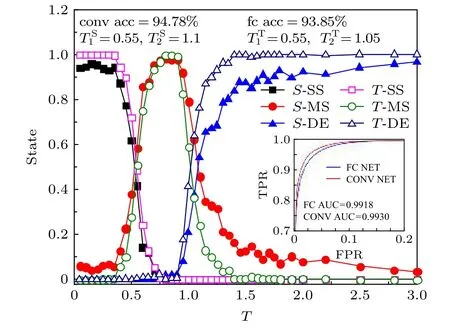
圖6 神經網絡訓練的識別結果圖 橫坐標為溫度,縱坐標State表示每個溫度下的樣本被識別為某個狀態的概率,圖標中S表示狀態標記法,T表示溫度標記法,SS表示單條紋吸附態,MS表示多條紋吸附態,DE表示脫附態.其中卷積網絡的識別率為94.78%,AUC值為0.9930,全連接網絡為93.85%,AUC值為0.9918,狀態標記法的臨界相變溫度 T1=0.55 ,T2=1.1,溫度標記法的臨界相變溫度T1=0.55,T2=1.05Fig.6.A plot of the result of the neural network training.The x-axis is the temperature,the State indicates the probability that the sample at each temperature is recognized as a certain state,S indicates the state labeling method,T indicates the temperature labeling method,SS indicates the single-striped adsorption state,MS indicates the multistriped adsorption state,and DE indicates desorbed state.The figure shows the learning results of two kinds of labeling methods.The recognition rate of convolutional network is 94.78%,where the AUC value is 0.9930.the fully connected network is 93.85%,where the AUC value is 0.9918,and the critical phase transition temperature of state labeling method is 0.55 and 1.1.The critical phase transition temperature of the temperature labeling method is 0.55 and 1.05.

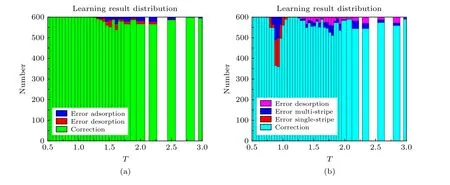
圖7 神經網絡學習結果的分布圖 (a) 均質表面下的學習結果分布,綠色表示識別正確的樣本,其他的表示識別錯誤的樣本;(b) 條紋表面下的學習結果分布,藍色表示識別正確的樣本,其他的表示識別錯誤的樣本Fig.7.The distribution of neural network learning results：(a) the distribution of learning outcomes on the homogeneous surface,green indicates that the correct sample,and other samples that identify the error; (b) the distribution of learning results on the pattern-stripe surface,blue indicates that the correct sample,and other samples that identify the error.

從圖7中可以看出,識別錯誤的樣本主要集中在臨界相變點附近,這是因為該附近的有限鏈長樣本自身屬于哪一個態的典型特征不明顯,容易被識別為相鄰狀態中的另一個狀態,因此誤判的可能性比較高.該結果也說明了隨著臨界相變點的增多增加了模式識別的復雜性,其識別率也隨之下降.

4 結 論

本文采用MC模擬和神經網絡研究了高分子鏈在吸附表面的狀態以及吸附相變的計算.研究表明神經網絡可以識別高分子鏈在均質表面的脫附與吸附狀態,從而可以確定其吸附相變.即使在每個溫度選取較少的樣本數也可以獲得比較高的高分子鏈狀態識別率.分別采用溫度標記法和狀態標記法對高分子鏈構象樣本進行標記,研究發現采用這兩種方法所得到的臨界相變點基本相同,高分子鏈在均質表面的吸附相變點 TC=1.5 ,在條紋表面的多條紋向單條紋的相變點 T1=0.55 和脫附態與吸附態之間的相變點為 T2=1.1.總之,經過訓練的神經網絡對高分子鏈的構象狀態具有較高的識別能力,人工神經網絡為高分子物理的模擬計算研究提供了一種新的途徑.