非對易施瓦西黑洞的熱力學及其量子修正*

沈玨 劉成周 朱寧寧 童一諾 嚴晨成 薛珂磊

(紹興文理學院物理系,紹興 312000)

為了探討量子引力效應對黑洞量子性質的影響,本文研究了非對易黑洞的熱力學及其量子修正.首先,利用修正的黑洞熱力學第一定律,對非對易施瓦西黑洞的熱力學量進行了計算.結果表明,利用修正的熱力學第一定律得到的非對易黑洞溫度與利用表面引力和隧穿方法得到的溫度相同,而且黑洞熵符合貝肯斯坦-霍金面積定律.對得到的黑洞熱容進行分析,發現在視界半徑與非對易參數滿足一定條件時,熱容可以為正值,非對易黑洞可以具有熱力學穩定性.其次,討論了廣義不確定原理對非對易施瓦西黑洞熱力學的影響,給出了廣義不確定原理修正的黑洞溫度、熵和熱容表達式,其中得到的黑洞熵包含面積對數項.在忽略廣義不確定原理效應的情況下,修正的黑洞熵可以回到貝肯斯坦-霍金面積定律的情況.同樣,修正的黑洞溫度和熱容也可以在忽略量子引力效應時回到通常施瓦西黑洞的情況.

1 引 言

霍金從半經典的量子場論出發,表明黑洞并非只進不出,它能向外發出熱輻射[1,2].這可以描述為：由于真空量子漲落,黑洞附近產生正負粒子對,當負能粒子被黑洞吸收后,正能粒子可以因視界附近的時空彎曲效應而留在黑洞外,并可運動到無窮遠處,從而可在視界外觀測到黑洞釋放了粒子,這種現象被稱為霍金輻射.霍金輻射確立了黑洞溫度的存在和黑洞熱力學定律的成立,從而為黑洞熱力學奠定了基礎[3,4].黑洞熱力學體現了廣義相對論和量子理論之間深刻的內在聯系,揭示了黑洞的量子性質.同時,黑洞熱力學也帶來了黑洞信息疑難等理論物理的難題[4,5].一般認為,揭示黑洞熱力學的本質和解決黑洞熱力學疑難需要相對論與量子力學的進一步結合甚至統一.

引力量子化是理論物理面臨的巨大挑戰,量子引力理論還有待建立.存在普朗克長度量級的最小可觀測長度是各種量子引力候選理論的普遍預言[6].最小長度引發了許多量子引力效應,其中最引人注目的一個是廣義不確定原理(generalize uncertainty principle,GUP)[7,8].當量子引力效應起重要作用時,由于存在長度和位置不確定度的最小值,此時海森伯不確定原理不再準確,需要引入與動量相關的不確定度的附加項.不確定原理是量子力學中的基本原理,對廣義不確定原理的研究及其應用非常重要和有意義(其綜述可見文獻[9]).將廣義不確定原理引入黑洞熱力學,可以研究黑洞熱力學性質的量子修正,并對黑洞熱力學疑難給出可能的解決方案[10-25].比如,廣義不確定原理可以克服黑洞視界附近量子態的發散困難,有助于對黑洞熵統計起源的認識; 廣義不確定原理可以影響黑洞視界上粒子的量子隧穿過程,增加粒子的隧穿概率,有助于對黑洞信息疑難的解決; 利用廣義不確定原理研究黑洞熵,可以得到熵的量子修正項,有助于對黑洞熵量子本質的認識; 利用廣義不確定原理研究黑洞輻射,可以得到普朗克量級的黑洞剩余,有助于對黑洞信息疑難問題的解決,并對暗物質給出可能的候選方案.

最小可觀測長度效應也引發了對非對易時空(noncommutative spacetimes,NS)的研究[26,27].在非對易時空中,廣義相對論的經典時空被具有非對易坐標的幾何取代,從而導致了一種量子修正時空-非對易黑洞(noncommutative black hole,NBH)[28-32].非對易黑洞中心存在非奇異的標量曲率,從而可避免傳統黑洞中的時空奇異性和溫度發散[33-36].非對易黑洞的正規性可以為黑洞熱力學疑難的解決提供線索和思路,相應地,其熱力學的修正效應也得到了許多研究[37-51].其中,通過考察正規黑洞的內能特征,文獻[51]提出,傳統的黑洞熱力學第一定律不再適用于能量密度依賴于黑洞質量的正規黑洞; 正規黑洞的內能和熱力學第一定律需要修正.利用文獻[51]給出了修正的黑洞熱力學第一定律,文獻[23]研究了Hayward正規黑洞熱力學的量子修正,得到了不同方法下黑洞溫度結果的一致性,并驗證了貝肯斯坦-霍金面積定律適用性.

此外,關于最小長度和黑洞熱力學的量子修正,還有許多其他研究和進展,均增加了對黑洞量子性質的認識[52-63].其中,Parikh 和 Wilczek[62,63]給出了一種通過計算視界上粒子的隧穿率來給出霍金輻射的半經典方法.量子隧穿方法將粒子的隧穿概率與黑洞熵的變化相聯系,給出了霍金輻射偏離黑體譜的結果,從而可以給出一種可能的解決黑洞信息疑難的方案.

為了研究最小長度效應對黑洞量子性質的影響,我們研究了非對易黑洞的熱力學.研究中利用熱力學第一定律的修正形式,并考慮廣義不確定原理效應.首先,我們在非對易施瓦西黑洞中,利用修正的黑洞熱力學第一定律,計算了黑洞的溫度、熵和熱容,給出了具有普遍意義的黑洞溫度表達式,討論了黑洞的面積定律的適用性和熱力學穩定性.其次,將廣義不確定原理與時空的非對易效應相結合,討論了廣義不確定原理對非對易施瓦西黑洞熱力學的影響,得到了廣義不確定原理修正的黑洞溫度、熵和熱容.本文第2節對非對易黑洞做簡單介紹; 第3節利用修正的熱力學第一定律對非對易施瓦西黑洞的熱力學性質進行討論; 第4節討論廣義不確定原理對非對易黑洞溫度、熵和熱容的影響; 最后是總結和討論.本文將采用G=k=c=1的自然單位制.

2 非對易黑洞

廣義相對論指出,引力是時空彎曲的表現,而時空彎曲源于物質與能量.在對易空間中,點粒子質量密度通常用質量與狄拉克函數的乘積來表示.考慮非對易性對引力物體中質量分布的影響,質量密度不再能用狄拉克函數表示,而是要用高斯分布替代[28-30].相應地,時空結構的描述將發生變化.

在非對易時空中,存在空間坐標x的非對易關系[26,27]

其中,θ 為非對易參數,具有普朗克長度平方的量級.(1)式表示,空間出現了模糊性,對易空間中描述位置的幾何點將被最小寬度為普朗克長度量級的區域所取代.因此,利用狄拉克函數來定義質點密度的方法在非對易空間中不再適用,而是要用最小寬度為普朗克長度的高斯分布.對于靜態、球對稱的點粒子引力源,其質量分布可用密度 ρθ表示為[28-30]

其中M為引力源的質量.可以看到,在非對易空間中,取代對易空間中的點粒子,質量M將在整個區域上分布,其特征尺度為利用質量密度(2)式,可以求出半徑為r范圍內引力源的總質量為

求解具有非對易質量密度的愛因斯坦方程,可以得到非對易時空中的黑洞解[28-30].在廣義相對論中,對于非對易性的影響,可以考慮通過保持愛因斯坦場方程左邊張量的標準形式,而在右邊引入一個修改后的能量動量張量并將時間分量記為為使度規的時間分量滿足利用能動張量的協變守恒能動張量可定義為

這樣,利用能動張量(5)式解愛因斯坦場方程,可以得到非對易時空中的施瓦西黑洞線元為

其中,r為徑向坐標,d?2為單位球面上的度規,且有[28-30]

這樣,非對易黑洞可以在 r=0 處找到一個正常數曲率的德西特核,不存在曲率奇點.而且,這一時空非奇異性可以對黑洞的蒸發等熱力學性質產生實質性的影響[33-36].而如果忽略時空的非對易性,令 θ→0 ,即可通過(9)式在 r=0 處得到時空奇點.

3 非對易黑洞的熱力學

接下來研究非對易施瓦西黑洞的熱力學.首先,通過三種方法,即表面引力法、量子隧穿法和熱力學第一定律法來給出非對易黑洞的溫度.將會看到,由熱力學第一定律得到的黑洞溫度與其他兩種方式所得的不同.為了解決這一矛盾,我們采用文獻[51]給出的修正的黑洞熱力學第一定律.可以看到,利用修正的黑洞熱力學第一定律,可以得到與表面引力法和量子隧穿法一致的黑洞溫度,并得到符合貝肯斯坦-霍金面積定律的黑洞熵.進一步,計算非對易黑洞的熱容,得到非對易施瓦西黑洞可以具有熱力學穩定性的結果.

首先,通過表面引力法給出非對易黑洞(6)式的溫度.利用(6)式和(7)式,通過 [(gθ)tt]r=rh=0 ,可得黑洞的視界半徑為

黑洞視界上的表面引力 κ 是一個守恒量,由視界的幾何結構決定,即

霍金輻射是黑洞附近的量子效應.黑洞溫度是黑洞視界的特征量,可由視界上的表面引力得到[2],

對于利用表面引力所得到的非對易施瓦西黑洞的溫度,可以看出,對于大黑洞,即時,溫度Tκ可以回到施瓦西黑洞溫度但對于小黑洞,Tκ將與 TSch有明顯不同[28-30].

利用霍金輻射的量子隧穿方法同樣可以計算黑洞的溫度[62,63].對于球對稱靜態時空,利用Wenzel-Kramers-Brillouin近似,粒子在視界上的輻射率 Γ 可以從隧穿粒子作用量I的虛部得到[62,63],即

為了計算粒子在視界上的隧穿作用量,需要消除線元(6)式的坐標奇異性.因此,對該線元進行Painleve坐標變換[64]

從而得到

可以看出,Painleve坐標線變換可以消除度規在視界上的奇異性.

為了計算無質量粒子在視界上的隧穿率,需要給出粒子的徑向運動方程.從(15)式可以得到徑向零測地線方程為

其中“+”對應出射粒子,“-”對應入射粒子.這里,為了研究視界外的輻射,我們取“+”.對(16)式在視界上進行泰勒展開,可以得到

粒子隧穿作用量虛部為

其中,ri和 rf表示粒子在隧穿前后的坐標,pr為粒子的動量.應用哈密頓方程

并改變(18)式的積分次序,可以得到

其中H為系統的哈密頓量,ω′表示隧穿粒子的能量.將粒子徑向運動方程(16)式代入(20)式中,并取(17)式的一級近似,可以得到

利用留數定理,完成對r的積分,得到

將(22)式代入(13)式,得到

這樣,將(23)式與玻爾茲曼因子 exp(-ω/T) 相比較,得到黑洞的溫度為

可以看到,通過量子隧穿方法得到的黑洞溫度與通過表面引力得到的黑洞溫度是相同的.

利用黑洞熱力學第一定律也可以計算黑洞溫度.對于無轉動無電荷的非對易黑洞,黑洞熱力學第一定律為

其中,S為黑洞的熵,TH為黑洞的熱力學溫度.對于非對易黑洞(6)式,其質量可以通過 f(rh)=0 表示為

按照貝肯斯坦-霍金面積定律,黑洞熵可以表示為

其中 Ah為黑洞視界面積.將(26)式和(27)式代入(25)式,即可根據熱力學第一定律得到非對易施瓦西黑洞的溫度為

其中,參量 B(rh,θ) 定義為

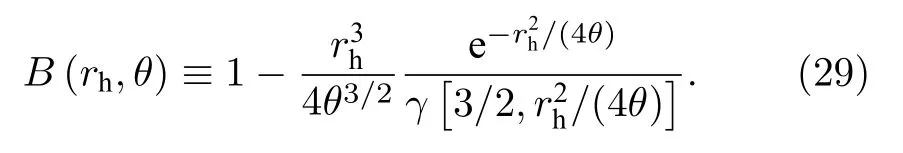
可以看出,由黑洞熱力學第一定律所得出的黑洞溫度(28)式與表面引力溫度(12)式和量子隧穿溫度(24)式并不一致.如果熱力學第一定律是適用的,那么利用熱力學第一定律得到的溫度與其他方法得到的溫度也應該是一致的.實際上,對于包括廣義相對論在內的各種引力理論中的大多數黑洞來說,確實是這樣的.但對于非對易黑洞,出現了與熱力學第一定律有關的矛盾.一方面,三種方法給出了兩個不同的黑洞溫度,而表面引力與隧穿效應得到了同樣的結果.因此,我們傾向于由表面引力和隧穿效應所得到的結果,即由通常的熱力學定理得到的溫度(28)式需要修改.另一方面,研究表明,即使是利用表面引力和隧穿效應所得的霍金溫度,也不能在非對易黑洞中利用熱力學第一定律得到滿足面積定律的貝肯斯坦-霍金熵[36-39].非對易效應只作用于物質源,而場方程的愛因斯坦張量部分保持不變,而且非對易性只有在普朗克尺度下才有作用,因此,作為視界特征量的黑洞熵,在非對易黑洞時空中也應該符合貝肯斯坦-霍金面積定律.這樣,在非對易黑洞中,認為(12)式和(24)式是正確的溫度表達式,而且黑洞熵滿足面積定律,則傳統的黑洞熱力學第一定律需要修改.對于包括非對易黑洞在內的正規黑洞,文獻[51]給出了一種修正的熱力學第一定律.利用該修正的熱力學第一定律,可以避免正規黑洞中與通常的熱力學第一定律有關的矛盾.

文獻[51]從考察黑洞的內能入手,認為正規黑洞的內能不應與黑洞的質量直接等同,而應存在一個修正因子.實際上,彎曲時空中的能量本來就對理論模式和定義方法有較復雜的依賴性,是需要進行研究的課題[65].這樣,考慮黑洞內能的修改,則修正后的黑洞熱力學第一定律應為[51]

這里,F(M,rh) 為內能修正因子,且

對于非對易施瓦西黑洞(6)式,由(5)式可見

因此,可以得到非對易黑洞的內能修正因子為

這樣,將修正因子(33)式代入(30)式,并應用面積定律,可以通過修正后的熱力學第一定律得到黑洞的溫度為

顯然,這是與(12)式一樣的結果.這就是說,由修正的黑洞熱力學第一定律得到的非對易黑洞溫度,與利用表面引力法和量子隧穿法得到的黑洞溫度是一致的,即有

另外,根據修正的熱力學第一定律,可以得到非對易施瓦西黑洞的熱力學熵為

將(33),(34)和(26)式代入(36)式,計算可得

這樣,利用修正的熱力學第一定律,驗證了在非對易施瓦西黑洞中黑洞熵滿足面積定律.

接下來,計算非對易施瓦西黑洞的熱容,以討論時空非對易性對黑洞熱力學穩定性的影響.黑洞的定體熱容定義為

對于施瓦西黑洞,將溫度 (Th)Scw=h/(8πM) 與熵(37)代入(38)式,則有

施瓦西黑洞的熱容為負,表示該熱力學系統不穩定[4].施瓦西黑洞會隨著霍金輻射變得更小,同時溫度更高,這會加劇黑洞的輻射從而使得輻射無法被阻止,而且當黑洞半徑趨近于零時,會出現輻射爆炸.

對于非對易施瓦西黑洞(6)式,將溫度(34)與熵(37)式代入(38)式,可得

這是一個較復雜的熱容公式,但當 θ→0 時,該式可以給出(39)式的結果.這就是說,忽略非對易效應,(40)式即為施瓦西黑洞的熱容.比如,對于大質量黑洞,當時,(40)式可回到施瓦西黑洞的熱容(39)式.

另外,為了方便對黑洞熱力學性質的討論,可以對黑洞溫度進行近似處理[28-30].在的情況下,將展開至的同階項,可以將非對易施瓦西黑洞的溫度(34)式改寫為

可以看出,對于大質量黑洞,非對易施瓦西黑洞低于同質量的施瓦西黑洞溫度這是非對易黑洞與通常黑洞的一個熱力學差異.而且,當時,非對易黑洞與de-Sitter時空相符[28-30],而此時施瓦西黑洞的溫度會趨于發散.不過,當黑洞的大小符合時,非對易施瓦西黑洞的溫度可以回到施瓦西黑洞的溫度.

對于大質量黑洞,將溫度(41)式與熵(37)式代入(38)式,可得到較為簡單的熱容公式

與(40)式一致,該式也可以在大黑洞極限情況下,回到施瓦西黑洞的熱容(39)式.

如果黑洞熱容為正,則黑洞有可能與外界達到熱力學平衡.現在我們考察非對易黑洞熱容為正的可能性.為方便,定義

在(42)式中令 CV＞0 ,可以得到

解不等式(44),可以近似得到 1.54＜μ＜5.63.這樣,結合(43)式,可以看到,當黑洞半徑滿足

時,非對易施瓦西黑洞的熱容大于零,黑洞可以具有熱力學的穩定性.也就是說,處于這一尺度范圍內的非對易施瓦西黑洞,可以與外界達到熱力學平衡,黑洞可以在熱浴中穩定存在.顯然,這是非對易施瓦西黑洞不同于施瓦西黑洞的熱力學性質.

4 廣義不確定原理對黑洞熱力學的影響

為了進一步討論黑洞熱力學的量子修正,我們考慮廣義不確定原理對非對易黑洞相關熱力學量的影響.考慮引力的量子效應,海森伯不確定原理ΔpΔx≥?可被推廣為如下形式的廣義不確定原理[6-10]：

考慮到通常 lp?Δx ,對上式進行泰勒展開,保留到的二次項,得到

利用海森伯不確定原理,可以給出粒子的能量ω≥?/Δx[66].這樣,考慮(48)式給出的廣義不確定原理,粒子能量的修正值為

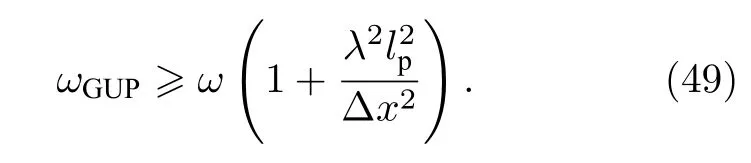
然后,將(49)式代入(23)式,得到廣義不確定原理修正下的粒子隧穿概率為[20-23]

將(50)式與玻爾茲曼因子 exp(-ω/T) 比較,可得

取輻射粒子的位置不確定度為 Δx?2rh[19],且將(24)式和(35)式代入上式,可得廣義不確定原理修正的黑洞溫度為

可以看到,黑洞的溫度出現了與廣義不確定原理相關的修正因子,而且有

即廣義不確定原理體現的量子引力效應降低了黑洞的溫度.如果忽略廣義不確定原理的修正效應,令 λ→0 ,則有 TGUP=Th.同樣,對于大質量黑洞,考慮到為小量,廣義不確定原理對黑洞溫度的影響可以忽略.但對于小質量黑洞,(52)式表明,TGUP可以與 Th有明顯不同,這也許有可能給廣義不確定原理帶來可觀測效應和相應檢驗.

現在,考慮到廣義不確定原理對黑洞溫度的影響,利用修正的熱力學第一定律(30)式,非對易施瓦西黑洞的熵可以表示為

將(26)式,(33) 式和(52)式代入(54)式,計算得

忽略積分常數,計算結果可以表示為

這樣就得到了廣義不確定原理影響下的非對易施瓦西黑洞熵.其中,第一項是貝肯斯坦-霍金熵,第二項是與廣義不確定原理效應有關的黑洞熵的量子修正,該修正為黑洞面積的對數.忽略廣義不確定原理效應,令 λ→0 ,則黑洞熵可以回到(37)式的面積定律.而考慮到 λ 具有普朗克長度量級,可以看出,在大黑洞情況下,rh?λlp,(56)式中起主導作用的是第一項,可以體現黑洞熵正比于黑洞面積.而在黑洞半徑接近普朗克長度時,廣義不確定原理對黑洞熵的影響不可以被忽略,熵與面積不再成正比.另外,這里的修正熵(56)式與相關研究結果是相符合的[19-23].

考慮廣義不確定原理效應,黑洞的熱容公式(38)可以寫為

將(56)式和(52)式代入(57)式得

再將(34)式代入(58)式,可以得到進一步的計算結果為

此即廣義不確定原理影響下的非對易施瓦西黑洞的熱容.可以看出,當令 λ→0 時,(CV)GUP可以回到 (40)式,即與不考慮廣義不確定原理修正效應的熱容結果一致.然后,再令 θ→0 時,可以得到施瓦西黑洞的熱容(39)式.

另外,在(59)式中,直接令 θ→0 ,可以得到此為考慮廣義不確定原理效應時的施瓦西黑洞熱容.然后,再令 λ→0 ,(60)式也可以回到施瓦西黑洞的熱容(39)式.這是與相關研究相符合的結果[25].

5 總結與討論

本文研究了具有正規性的非對易黑洞的熱力學性質.首先,我們分別利用表面引力、隧穿效應與黑洞熱力學第一定律計算了非對易施瓦西黑洞的溫度.結果表明,由表面引力與隧穿效應所得的黑洞溫度相同,而由傳統熱力學第一定律所得的黑洞溫度與上述兩種方法所得的溫度不一致.文獻[51]提出,對于包括非對易黑洞在內的一類正規黑洞,由于時空質量分布與經典黑洞有所不同,熱力學第一定律應進行相應修正.利用文獻[51]給出的黑洞熱力學第一定律的修正形式,并應用黑洞面積定律,我們得到了與其他兩種方法一致的黑洞溫度.這樣,在非對易施瓦西黑洞中,利用三種不同的方法,均得到了一樣的黑洞溫度.而且,該溫度表達式表明,非對易黑洞的溫度比相應的施瓦西黑洞溫度低.不過,對于大質量黑洞,非對易黑洞溫度與施瓦西黑洞溫度的差異會消失.隨后,利用修正的黑洞熱力學第一定律,計算了非對易施瓦西黑洞的熵,結果驗證了非對易黑洞符合貝肯斯坦-霍金面積定律.然后,根據得到的溫度和熵,并利用修正的熱力學第一定律,得到了非對易施瓦西黑洞的熱容.對熱容結果進行分析,近似得到在視界半徑與非對易參數滿足一定條件時,非對易施瓦西黑洞的熱容可以為正值.這是與傳統施瓦西黑洞的負熱容不同的熱力學性質.這表明,非對易黑洞有可能與外界達到熱力學平衡,黑洞可以在一定尺度范圍內穩定存在.而在大質量極限下,非對易施瓦西黑洞的熱容會回到施瓦西黑洞的情況.

其次,我們考慮廣義不確定原理體現的量子引力效應,并利用修正的黑洞熱力學第一定律,對非對易施瓦西黑洞的熱力學進行了進一步研究.結果表明,廣義不確定原理對黑洞溫度、熵和熱容均帶來進一步的量子修正.廣義不確定原理進一步降低了黑洞的溫度.對于微觀黑洞來說,這一溫度差異有可能帶來觀測上的區別,并可能對廣義不確定原理的量子引力效應進行檢驗.廣義不確定原理為黑洞熵提供了一個面積對數的修正項.而在大黑洞極限下,對數項影響可以忽略,黑洞熵符合面積定律.當黑洞減小至接近普朗克尺度時,量子引力效應不能被忽略,黑洞熵不再符合面積定律.對于廣義不確定原理影響下的黑洞熱容,可以看到,忽略廣義不確定原理效應,黑洞熱容回到之前的非對易黑洞熱容,再忽略非對易效應,黑洞熱容回到傳統施瓦西黑洞情況.而在修正的熱容公式中,如果直接忽略非對易效應,則可得到廣義不確定原理影響下的施瓦西黑洞熱容,再忽略廣義不確定原理效應,也可得到傳統施瓦西黑洞熱容.

黑洞熱力學是量子引力效應的重要應用和探測領域,特別是在量子修正黑洞中.廣義不確定原理在描述黑洞的量子性質中起著重要的作用.本文的研究可推廣到帶電荷和帶角動量的非對易黑洞中.另外,在此基礎上,研究非對易黑洞蒸發的量子修正,以及相關的輻射剩余和信息疑難等問題,也應是值得繼續的工作.