微納尺度體點導熱的拓撲優化*

李含靈 曹炳陽

(清華大學工程力學系,熱科學與動力工程教育部重點實驗室,北京 100084)

體點導熱問題是電子器件散熱優化方面的基礎問題之一,已有研究大多建立在傅里葉導熱定律的基礎上,但隨著電子器件的特征尺度降低到微納米量級,導熱優化需要考慮非傅里葉效應.本文結合聲子玻爾茲曼方程的數值解和對聲子平均自由程進行插值的固體各向同性材料懲罰方法,發展了微納米尺度下彈道-擴散導熱的拓撲優化方法.在彈道-擴散導熱機制下,體點導熱的拓撲優化得到的材料分布明顯不同于擴散導熱下的樹狀分布,且會隨努森數的變化而變化,與拓撲優化的插值方式和聲子彈道輸運有關.隨著彈道效應的增強,尺寸效應使得材料分布中微小結構的等效熱導率低于粗壯結構,因而拓撲優化結果朝著增多粗壯結構、減少微小結構的方向發展.彈道效應足夠強時,填充材料聚集在低溫邊界附近,主干和枝合并,呈團狀分布.

1 引 言

以芯片為代表的電子器件,在當代社會中扮演著不可替代的重要角色.隨著電子器件向小型化、集成化的方向發展,器件的特征尺寸已經降低至微納米量級[1],器件內的功率密度大幅增加.2012年,芯片內的平均熱流密度便已達到250 W/cm2左右[2].高功率密度會讓電子器件溫度升高,產生局部熱點,導致其可靠性和壽命顯著下降[3].因此,電子器件的熱管理已經成為相關領域發展面臨的關鍵挑戰之一[4-7].根據電子器件內熱點分布和傳熱結構布局等因素,進行散熱仿真和優化改進,對實際產品的設計和制造有著重要意義.

在芯片內部填充高導熱材料以加強導熱是提高芯片散熱能力的主要途徑,考慮到芯片內空間寶貴,高導熱材料的添加數量必須受到限制,這樣的芯片散熱問題可以被抽象為體點(volume-to-point,VP)導熱問題[8],如圖1所示.給定體積的區域代表芯片,區域內的均勻內熱源代表焦耳加熱,產生的熱量通過邊界處一小段溫度為 T0的低溫熱沉流出,其余邊界絕熱.現提供數量有限的高導熱填充材料,希望尋找合適的填充材料分布方式,構造高導熱通道,讓整個系統的溫度(平均溫度或最高溫度)降到最低.關于體點導熱問題,人們采用多種優化方法進行了研究,包括構型理論[8]、仿生優化[9]、拓撲優化[10-13]、模擬退火和遺傳算法[14]等.盡管這些方法都能有效降低系統溫度、提高散熱能力,但所得的高導熱填充材料分布方式不盡相同,這與優化問題自身帶有的局部最優性和多解性有關.當優化問題改變時,不同方法的性能優劣也可能發生變化.在各類優化方法中,拓撲優化方法因其能夠改變結構的拓撲構型、具備理論上的最高設計自由度而受到人們的青睞.利用拓撲優化,設計者不僅可以實現設計對象某方面性能的顯著提升,而且所花費的設計時間更少,能得到傳統經驗之外的具有啟發性的新結果[15].體點導熱問題的拓撲優化會得到填充材料充分伸入內部區域、整體呈樹狀的材料分布,其散熱性能明顯優于其他方法所預測的結構[11].

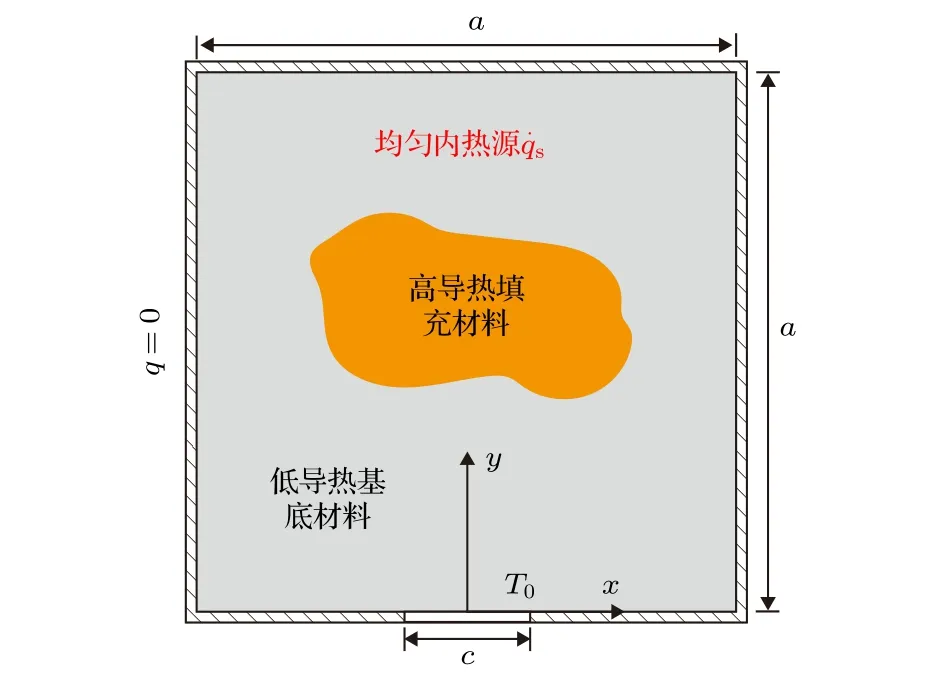
圖1 體點導熱問題示意圖Fig.1.The schematic diagram of the VP problem.

已有的導熱拓撲優化方法,都建立在經典的傅里葉導熱定律的基礎上[13],這在宏觀尺度下是合理的,但對微納米尺度下的導熱過程,傅里葉導熱定律不再成立[16-22],熱仿真及熱優化必須考慮非傅里葉效應.聲子是電子器件半導體中的主要載熱子[23],聲子彈道輸運和聲子相干是微納米尺度下發生非傅里葉導熱的兩個重要原因[5].聲子彈道輸運的強度可由努森數 Kn 來表征,其定義為材料聲子平均自由程l和系統特征尺寸L的比值,即Kn=l/L.宏觀尺度下,系統尺寸遠大于聲子平均自由程(Kn→0),聲子間散射充分,聲子按擴散方式傳遞,導熱過程遵循傅里葉導熱定律.但當系統尺寸與聲子平均自由程相當(Kn～1)甚至更小(Kn＜1)時,聲子不經歷散射而直接抵達邊界,這樣的過程稱為彈道輸運,會導致傅里葉導熱定律失效[24].在微納米結構中,部分聲子發生彈道輸運,其余聲子仍按擴散方式運動,對應的導熱機制稱為彈道-擴散導熱[25,26].聲子彈道輸運會引起熱導率的尺寸效應,表現為系統的等效熱導率與系統尺寸正相關,尺寸減小會造成等效熱導率降低[27,28],系統熱點溫度升高[29].此外,在給定溫度邊界處,由于彈道輸運的非平衡本質,邊界處的溫度并不連續,會出現溫度跳躍現象[30,31].聲子相干則主要出現在特征尺寸和聲子波長相當的系統中[32],例如石墨烯這樣的二維材料和超晶格這樣的特殊結構[33-35].聲子相干通過改變聲子群速度、弛豫時間和態密度等因素來影響導熱過程[36].對常用的半導體材料硅,室溫下聲子平均自由程約為300 nm[37],聲子波長小于10 nm[17],而目前大多數電子器件的特征尺寸在100 nm量級[1],故本文主要關注聲子彈道輸運引起的非傅里葉導熱.關于微納米尺度下彈道-擴散導熱過程的優化,前人曾結合動力學理論和拓撲優化來處理[38],但其優化目標只是特定點之間的溫差,無法考慮系統整體的溫度.目前,尚缺少適用于微納米尺度下彈道-擴散導熱過程的一般性優化方法,關于彈道效應對優化結果的影響也缺乏系統的認識.

本文結合聲子玻爾茲曼輸運方程(Boltzmann transport equation,BTE)和固體各向同性材料懲罰(solid isotropic material with penalization,SIMP)方法,發展了微納尺度下彈道-擴散導熱的拓撲優化方法.用聲子BTE代替傅里葉導熱定律作為導熱本構方程,以反映聲子彈道輸運; 用SIMP方法對聲子平均自由程的倒數進行插值以引入拓撲優化,并通過對相對密度變量全局梯度施加顯示約束的方法來確保解的適定性和網格無關性.將此方法用于體點導熱優化,發現彈道-擴散導熱機制下,拓撲優化預測的填充材料分布明顯不同于傅里葉定律下經典的樹狀分布,且會隨 Kn 的變化而變化,這與SIMP方法的插值方式和聲子彈道輸運有關.

2 優化方法

2.1 聲子玻爾茲曼輸運方程

聲子的運動規律符合聲子BTE,穩態、弛豫時間近似下的聲子BTE寫作

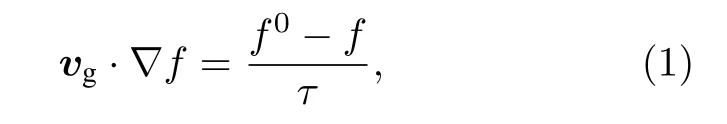
其中f是聲子分布函數; vg是群速度矢量; f0是平衡態聲子分布函數,即玻色-愛因斯坦分布; τ 是弛豫時間.聯合求解(1)式和能量守恒方程,就可以獲得聲子的微觀運動規律和分布函數,進一步可計算得到溫度、熱導率等宏觀熱性質.

本文選擇離散坐標法(discrete ordinate method,DOM)[39-41]來求解聲子BTE,此方法最早用于輻射輸運方程的求解,相關計算方法的發展較為成熟.根據聲子和光子的類比,可定義聲子輻射強度其中ω表示聲子頻率,D(ω)表示態密度,“”表示對聲子極化的求和.利用此定義,可以將聲子BTE轉化為聲子的輻射輸運方程(equation of phonon radiative transfer,EPRT)[42]

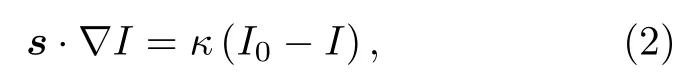
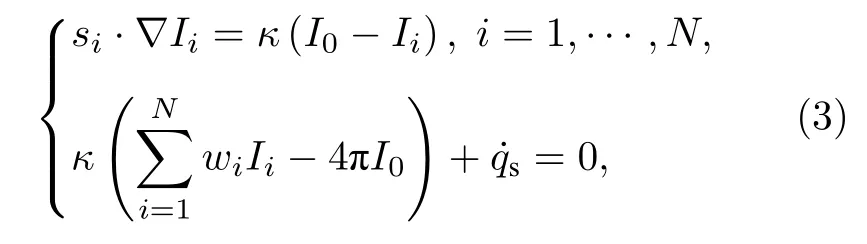
(3)式中包含N+1個等式,與未知的聲子輻射強度數量相對應,方程組封閉.

得到聲子輻射強度后便可計算溫度.聲子發生彈道輸運時,當地熱力學條件遠離平衡態,傳統的在熱平衡態下定義的溫度失去意義[43],而如何在這樣的非平衡態下定義溫度一直存在爭議[44].本文采用等效平衡溫度的概念[45,46],認為空間內某個離散單元在發射能量時,產生的聲子服從玻色-愛因斯坦分布,根據發射能量反解出的分布函數中的溫度,便是等效平衡溫度.使用DOM離散輻射強度后,等效平衡溫度的計算式為其中 σphonon是聲子斯特藩-玻爾茲曼參數[47].使用這種等效平衡溫度的好處是,在接近擴散導熱時,解聲子BTE所得結果能夠與傅里葉導熱定律的結果相吻合[39].

2.2 拓撲優化

拓撲優化本質上屬于大規模0-1整數規劃問題,區域內的每個點要么是空洞,要么是實體.這樣的離散優化問題在數學上是病態的,解的存在性、收斂性以及求解算法的實現都存在著巨大的困難[48].實現拓撲優化的關鍵是對優化問題進行適當的正則化處理,將設計變量由離散的變為連續的,從而能夠直接使用針對連續設計變量優化問題的求解方法.在這方面,SIMP方法[49]是經典而常用的技巧,其核心思想是將材料性質設定為關于相對密度的冪函數,從而將設計變量轉變為連續的相對密度.考慮到(2)式作為描述非傅里葉導熱的本構方程,僅有聲子消光系數 κ 是與材料類型有關的性質[38],于是本文提出對 κ 進行插值的SIMP方法來實現拓撲優化.空間中任意位置的消光系數寫作

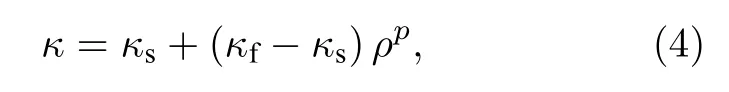
其中 ρ 是值在[0,1]區間上連續分布的相對密度變量; κs和 κf分別是基底材料和填充材料的消光系數,亦即各自聲子平均自由程的倒數; p是值大于1的懲罰因子.懲罰因子的作用是在優化過程中對介于0和1之間的中間密度值進行懲罰,使得 ρ 的值逐漸趨向于0和1兩個端點值,從而在優化結果中得到清晰的空洞(ρ=0)和實體(ρ=1)分布.關于SIMP方法插值方式的選擇,將在下一節結合優化結果做進一步討論.

即使采用SIMP方法,拓撲優化仍會面臨解的不存在性、不收斂性和不唯一性等問題,導致優化結果會出現棋盤格、網格依賴性等問題[50].為了得到可靠的優化結果,需要引入更多的正則化處理以抑制數值不穩定性.本文采用對相對密度變量 ρ 的全局梯度施加顯式約束的方法[15],即在目標函數中增加關于 ρ 的全局梯度的權重懲罰項,以約束ρ的變化程度.至此,可寫出通過求解EPRT來獲得溫度分布的二維體點導熱拓撲優化的數學模型為：

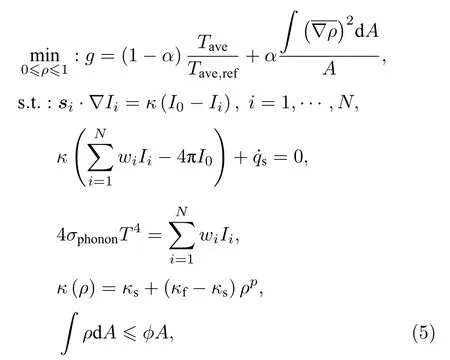
其中 Tave是系統平均溫度,Tave,ref是人為選取的參考溫度,α 是相對密度變量全局梯度的權重系數,是無量綱的相對密度變量梯度,A=a2是二維區域的面積,? 是預先給定的高導熱填充材料占整個區域的比例.對平均溫度和設計變量梯度進行無量綱化的目的是使二者通過線性求和構成實際的目標函數g.現在的模型以降低系統平均溫度為優化目標,如果目標是減小系統的最高溫度,則可以將優化對象變更為文獻[51]中提到的幾何平均溫度,其他設置不變.需要說明的是,因為本文的關注點是如何在導熱優化中考慮聲子彈道輸運并分析彈道輸運對優化結果的影響,所以優化模型中并未考慮不同材料之間的界面熱阻,這樣可以更直觀地反映彈道效應的影響.界面熱阻對現有優化結果的影響將在第3節中進行討論.

求解(5)式的拓撲優化的流程圖如圖2所示,包括以下步驟：1)初始化,對區域進行離散并任意給定一組 ρ 的初始值; 2)系統重分析,根據SIMP方法插值得到當前設計點對應的消光系數,再求解EPRT和穩態能量守恒方程獲得聲子輻射強度,進而計算平均溫度和目標函數; 3)靈敏度分析,計算目標函數和約束函數對設計變量的導數; 4)優化求解,根據導數信息,確定滿足約束且減小目標函數的設計變量演化方向(可行下降方向),并計算最佳步長,更新當前設計變量值; 5)收斂判斷,滿足收斂條件時結束迭代,輸出結果; 否則重復步驟2)-4).

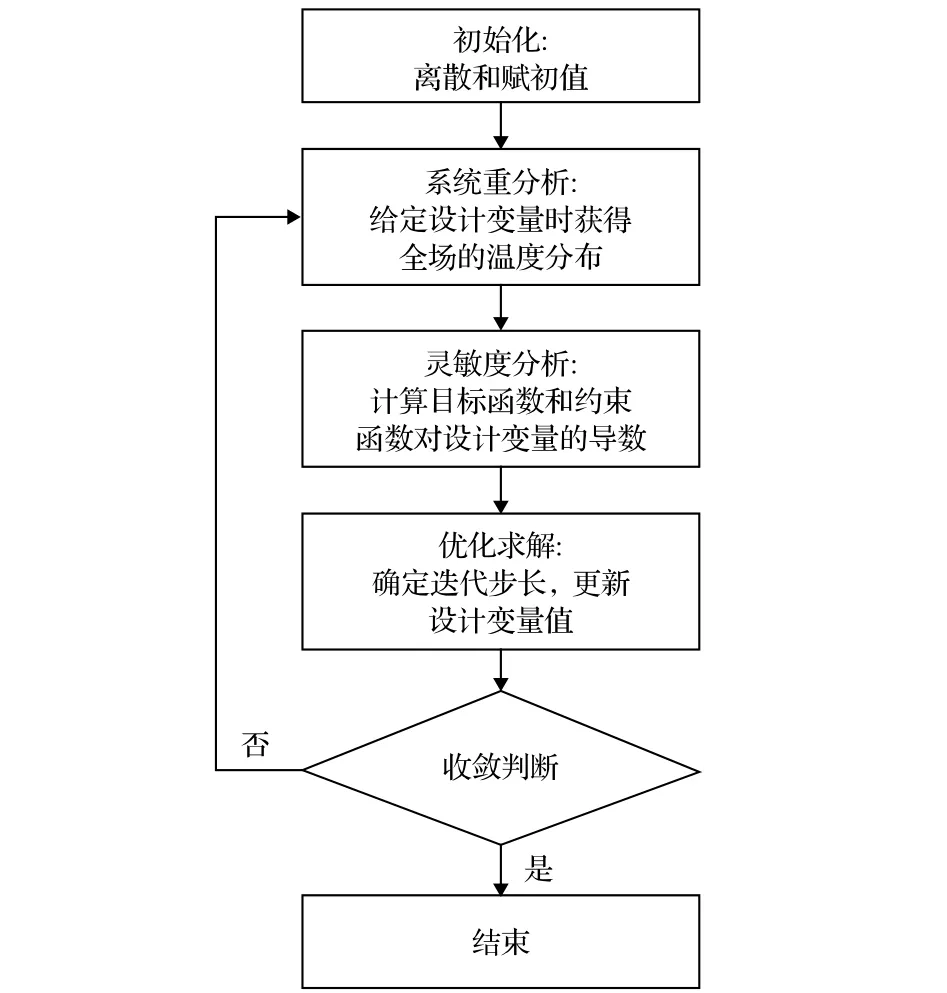
圖2 體點導熱拓撲優化的流程圖Fig.2.The flow chart of topology optimization for the VP problem.

3 結果與分析

在體點導熱問題中,設置低溫邊界與區域邊長的比值為 c/a=0.1 ,低溫邊界的溫度為 T0=300K ,填充材料體積占比為 ?=0.1 ,設計變量初始值取為 ρ=? ,即材料均勻分布.定義無量綱空間坐標為 X=x/a ,Y=y/a ,參考文獻[12]定義無量綱溫度其中 ks是基底材料熱導率,這樣無量綱化的好處是消除了內熱源功率、熱源面積、熱導率和邊界溫度具體值對優化結果的影響,使填充材料和基底材料間導熱性能差異成為優化結果的決定因素.在數值計算中,用數量為n×n的方形網格離散計算域,網格尺寸為 h=a/n.DOM的離散方向數設定為 N=24 ,此值既能避免求解溫度場時出現過強的“射線”效應[41],又不至于讓計算量過大.參考文獻[52],相對密度變量梯度的無量綱化方式為方法的懲罰系數取經典值 p=3.為了提高求解效率,對聲子BTE使用灰體近似,迭代過程中的靈敏度分析使用伴隨方法[53],優化求解則采用構造原問題局部近似模型的移動漸進方法(method of mo ving asymptotes,MMA)[54].收斂準則設定為其中上標j表示迭代次數,認為滿足此條件時設計變量、目標函數值都達到穩定.考慮到大部分區域為基底材料,用基底材料的平均自由程來計算努森數,即 Kn=ls/a.

3.1 擴散導熱的體點優化

在進行求解聲子BTE的拓撲優化之前,先在傅里葉定律適用的條件下實現體點導熱的拓撲優化,以檢驗所發展的拓撲優化方法.盡管凡是在實體和空材料間構造連續函數并對中間密度值進行懲罰的方法都可稱為SIMP方法,但通常都是對本構方程的系數進行插值[15].對基于傅里葉定律的拓撲優化,本構方程中與材料性質有關的系數是熱導率,對應SIMP方法的插值公式為k(ρ)=ks+(kf-ks)ρp,其中 kf是填充材料熱導率.此時,填充材料和基底材料導熱能力的差異通過熱導率比kf/ks來體現,kf/ks越大,傳導同樣熱量所需要的高導熱材料橫截面積越小,因而在相同的填充量下填充材料能夠更遠地延伸到區域內部,形成的樹狀結構的“樹枝”更為細長,優化效果也更好[12].對本文提出的優化模型,本構方程中與材料性質有關的系數是聲子消光系數 κ ,對應的插值公式為(4)式.根據動力學理論,熱導率和聲子平均自由程間的關系為其中C是材料比熱,v是聲子群g速度的大小.材料的比熱、群速度通常是確定的,于是有 kf/ks∝lf/ls,意味著不同材料導熱性能的差別主要源自聲子平均自由程的差別[55].此時(4)式中關于聲子消光系數 κ (=l-1)的插值,對應于傅里葉導熱定律下對熱導率倒數 k-1的插值,而非傳統的對熱導率k的插值.在 kf/ks=500 ,α=0.05 ,n=80的條件下,分別對k和 k-1進行插值,基于傅里葉導熱定律的拓撲優化得到的結果如圖3所示.設定 kf/ks=500 是為了讓填充材料和基底材料的導熱能力存在較大差異,更直觀地體現優化的效果,且實際電子器件中絕緣材料和導電材料的熱導率通常也相差2個數量級[1].文獻中關于傅里葉導熱定律下體點導熱拓撲優化的研究也大多采用此熱導率比值.圖3左側表示 ρ 在區域內的分布情況,白色代表基體材料(ρ=0),黑色表示填充材料(ρ=1),顏色越深意味著該位置的 ρ 值越接近于1;右側則是無量綱溫度 T?的分布.插值k的拓撲優化得到了充分伸入內部區域、含多個分岔和枝的樹狀填充材料分布,如圖3(a)所示,符合文獻[10-13]中的結果,對應的無量綱溫度平均值是插值 k-1的優化結果則由圖3(b)給出,填充材料集中在區域下半平面,與低溫邊界相接觸,向區域內伸展的過程中只形成了2處分岔,此時與圖3(a)相比,圖3(b)中填充材料的主干更短、更寬,枝數量更少,對應的平均溫度和最大溫度更高.在擴散導熱條件下,不同形狀、尺寸的填充材料熱導率相等,具有相同的構建高導熱通道的能力.為了降低溫度,填充材料要設法伸入內部區域,縮短高導熱通道和區域內熱源間的距離,所以圖3(a)的結果要比圖3(b)更好.受制于SIMP方法的插值方式,圖3(b)得到的是體點導熱優化的某個局部最優解,但填充材料仍然有向區域內伸展的趨勢.圖3的結果表明,SIMP方法的插值方式會影響拓撲優化的效果,對本構方程的系數進行插值是更合理的選擇.以傅里葉導熱定律為例,盡管插值 k-1的拓撲優化也能收斂,但對應的是優化問題的某個局部最優解,優化效果不如插值k的結果好.類似地,當導熱的本構方程變成(2)式時,SIMP方法應當對方程的系數 κ 進行插值.

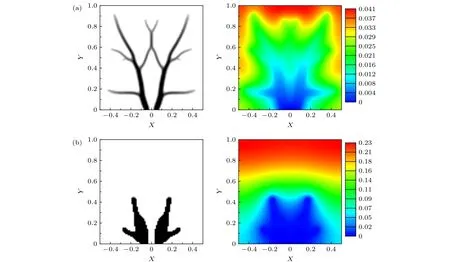
圖3 擴散導熱下不同插值方式對材料分布和溫度分布的影響 (a)插值k; (b)插值k-1Fig.3.The effect of interpolation ways on the material distributions and temperature distributions in diffusive heat conduction：(a) Interpolating k; (b) interpolating k-1.

圖4 擴散導熱下拓撲優化得到的材料分布隨 α 和n的變化Fig.4.The material distributions obtained by topology optimization in diffusive heat conduction varying with α and n.

除了SIMP方法的插值方式,α 的取值也很重要,因為 α 顯著響著拓撲優化解的數值穩定性[15].保持 kf/ks=500 不變,并使用對k的插值,擴散導熱條件下拓撲優化得到的填充材料分布隨 α 和n的變化如圖4所示.整體來看,填充材料的形狀都呈樹狀,與圖3(a)的結果大致相同,但細節上存在不少差異.當 α=0 時,隨著網格密度的增大,高導熱通道的主干周圍會出現越來越多狹長的末梢,這是因為拓撲優化的數值解天然地存在著網格依賴性.當 α=0.05 時,由于引入了對設計變量全局梯度的約束,拓撲優化結果的網格依賴性得到有效抑制,網格細化并未導致太多狹長末梢.進一步增大到 α=0.1 ,不同網格密度下拓撲優化結果間的差異更小,網格無關性更好.但是,比較相同網格密度的拓撲優化結果發現,增大 α 的值后,中間密度值對應的灰色區域增多,填充材料和基底材料之間的邊界變得模糊,這是控制設計變量全局梯度的代價.綜合考慮后,本文的拓撲優化選擇 α=0.05 ,n=80,此時所得結果具有較好的網格無關性和較清晰的材料邊界,且計算量相對較少.

3.2 彈道-擴散導熱的體點優化

根據上文確定的參數設置,對(5)式進行數值迭代,獲得了體點導熱在彈道-擴散導熱機制下的拓撲優化解.設定 lf/ls=500 以便和傅里葉導熱定律下的結果對比,不同 Kn 下優化得到的材料分布和溫度分布如圖5所示.總體來看,填充材料集中在區域下半平面,與低溫邊界充分接觸,其形狀完全不同于圖3(a)所示的伸入內部區域且含多個枝的樹狀結構,而與圖3(b)的材料分布更為接近.如3.1節所述,本文采用的插值 κ 的方法,對應于傅里葉定律下對 k-1的插值,因而優化結果與插值k-1的結果相似.可以預見的是,在 Kn→0 時,導熱過程接近純擴散導熱,優化會趨向于傅里葉定律下插值 k-1的結果.但受聲子彈道輸運的影響,圖5與圖3(b)仍然存在明顯的差異.當 Kn=0.002 時,低溫邊界處幾乎無溫度跳躍,區域內無量綱溫度的最大值略高于圖3(b)中的0.23,表明大部分聲子以擴散方式導熱,但仍有部分聲子發生了彈道輸運,這是因為填充材料的聲子平均自由程已和區域尺寸相當(lf～a).此時填充材料在低溫邊界處連通,主干呈“U”型,兩側共有6處外凸的細枝.增大 Kn 至0.01,靠近低溫邊界處 T?=0.06 ,發生了一定的溫度跳躍,則是0.44,約為圖3(b)結果的2倍,表明彈道效應增強.此時填充材料分布的“U”形主干開口變大、寬度變厚,枝數量減少為2個.當 Kn=0.1 時,填充材料的體聲子平均自由程已比區域尺寸大一個數量級,邊界處無量綱溫度的跳躍值接近0.6,區域內峰值溫度幾乎是圖3(b)結果的6倍,彈道效應已十分顯著.此時,填充材料聚集在低溫邊界附近,除了頂部有凹陷外,其它方向的伸展長度基本一致,主干和枝合并形成團狀分布.

為了檢驗所提出的拓撲優化方法的效果,分別在不同努森數下,對圖3和圖5中出現的5種材料分布進行熱仿真,得到的值列于表1,括號內的數據表示的值,即相對于材料均勻分布時的變化程度.表1顯示,不同努森數下,本文發展的拓撲優化方法所對應的值最低,如表中加粗數據所示,表明所預測的材料分布方式確實是最優的,驗證了聲子BTE和拓撲優化相結合的優化方法的正確性.以 Kn=0.1 時為例,解傅里葉定律的拓撲優化所得的材料分布,對應的值大概為80%,而解聲子BTE的拓撲優化得到的材料分布,對應的值在70%左右,進一步下降了10個百分點,其中又以Kn=0.1條件下的拓撲優化所得的構型效果最好,此外,對相同的材料分布方式,隨著 Kn 的增大,的值增大,表明添加高導熱材料所能帶來的優化效果變差.例如對圖3(a)所示的樹狀結構(擴散導熱條件下插值k的拓撲優化結果),Kn=0.002 時,是33.7%,但Kn=0.01時此值上升到53.2%,Kn=0.1 時只有86.0%.圖5和表1的結果共同表明,彈道-擴散導熱機制下,體點導熱問題的最佳材料分布會隨著彈道效應強度的變化而變化,基于傅里葉定律的拓撲優化所得的材料分布不再是最優的.因此,對微納米尺度下的散熱優化問題,在設計階段必須要考慮聲子彈道輸運的影響.值得一提的是,如果將現有優化模型中對 κ 的插值改為對其倒數l的插值,優化模型的收斂性會嚴重惡化,材料分布會出現嚴重的棋盤格問題和大量的中間密度值.

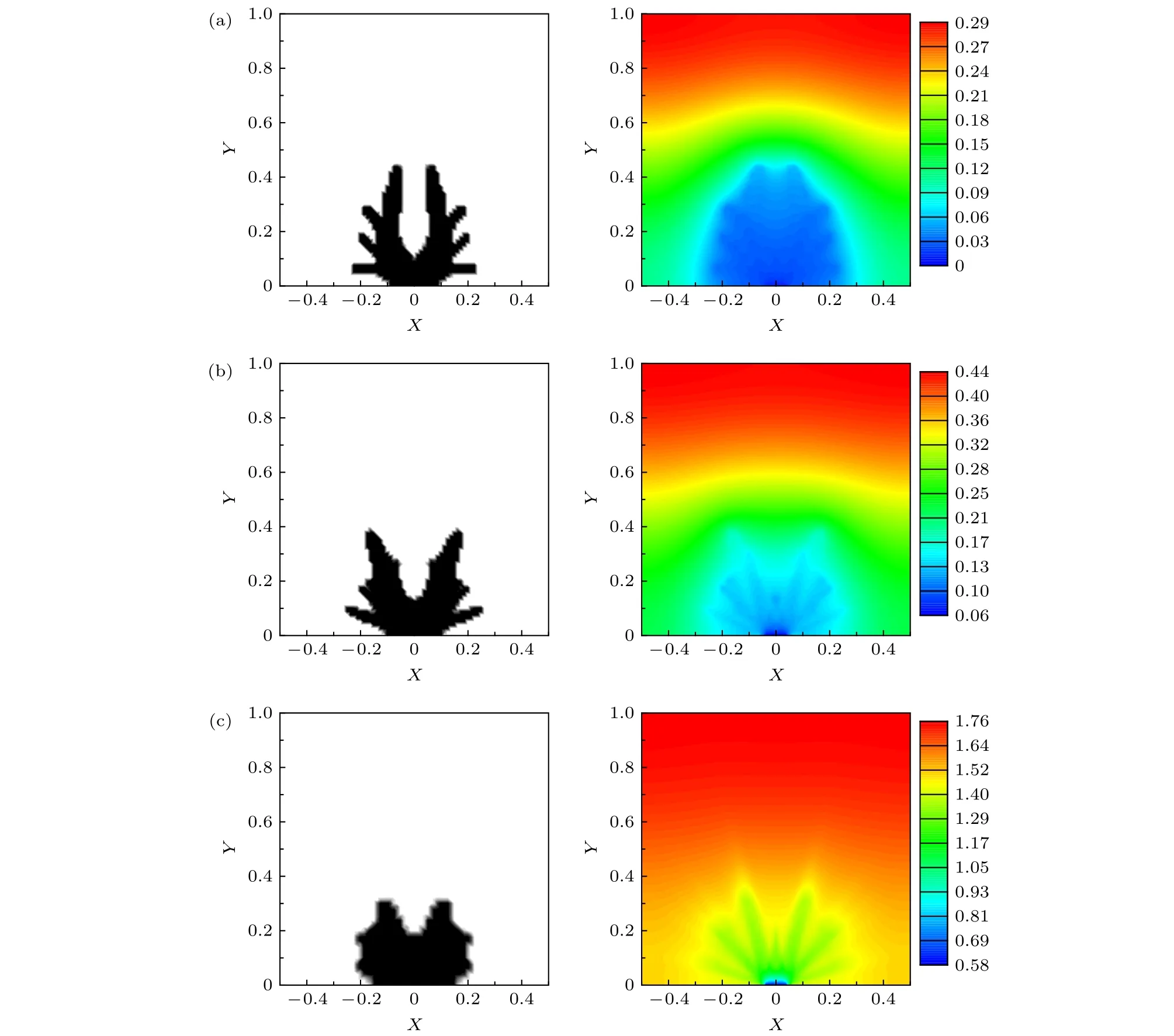
圖5 彈道-擴散導熱下拓撲優化的材料分布和溫度云圖隨 Kn 的變化 (a) Kn=0.002; (b) Kn=0.01; (c) Kn=0.1Fig.5.The topology optimization obtained material distributions and temperature distributions varying with Kn in ballistic-diffusive heat conduction：(a) Kn=0.002; (b) Kn=0.01; (c) Kn=0.1.

進一步分析圖5中拓撲優化得到的最優材料分布,發現隨著 Kn 的增大,彈道效應增強,填充材料從低溫邊界向內部區域發展的趨勢減弱,且分布形狀中微小的枝所占的比例減少,粗壯的主干所占的比例增多,這可以由彈道輸運產生熱導率的尺寸效應來解釋.不同于擴散導熱,彈道-擴散導熱機制下,結構的等效熱導率會隨尺寸的減小而降低.因為微小枝的尺寸比粗壯主干的尺寸更小,所以前者的等效熱導率比后者更低,前者在構建高導熱通道方面的性能不如后者; 且隨著彈道效應的增強,這種能力上的差別會增大.在 Kn 較小時,不同尺寸的填充材料間導熱性能差異較小,影響優化效果的主要還是熱源和高導熱通道的距離,所以圖5(a)的結果像圖3(b)那樣有一些分岔,且伸入內部區域較多.隨著 Kn 的增大,彈道效應增強,結構等效熱導率的降低對優化效果的影響加強,拓撲優化傾向于產生等效熱導率相對較大的粗壯結構,而非伸入內部區域的微小分散結構.Kn=0.1 時,盡管基底材料聲子平均自由程僅為系統特征尺寸的0.1倍,但填充材料的聲子平均自由程已經是系統特征尺寸的50倍,整個系統的彈道效應已十分顯著,團狀的填充材料分布在構建高導熱通道方面的性能最優,但由于填充材料比例限制,通道只能覆蓋低溫邊界附近的區域.彈道導熱極限下,拓撲優化的結果中填充材料聚集在低溫邊界附近,沿各個方向的伸展長度基本相同,呈半圓形團狀分布.圖5(c)的結果已經較為接近彈道極限下的結果.溫度分布中低溫區域的輪廓反映了填充材料所形成的高導熱通道的效果.在圖3和圖5中,低溫區域的輪廓都與填充材料的形狀大體一致,表明所有填充材料都有效地形成了高導熱通道.根據上述分析,在彈道效應較強時,如果填充材料的形狀中含有較多的微小結構,由于這些小尺寸結構在構建高導熱通道方面是低效的,對應區域的溫度將無法得到有效降低,溫度輪廓將勢必不同于填充材料的形狀.作為檢驗,給出擴散導熱條件下插值 k-1的拓撲優化所預測的材料分布(圖3(b))在 Kn=0.1 時的溫度場如圖6所示.盡管材料分布與圖3(b)相同,但圖6的溫度輪廓明顯不同于圖3(b),反而與圖5(c)的溫度輪廓更為接近,說明填充材料中粗壯的主干形成了高效的導熱通道,但細小的枝因為等效熱導率更低,所以在導熱方面是相對低效的,未能有效降低所在區域的溫度.

表1 不同材料分布在不同努森數下對應的無量綱溫度平均值Table 1.The average dimensionless temperature of different material distributions at different Knudsen numbers.

對體材料熱導率比值和界面熱阻對拓撲優化結果的影響做簡單說明.盡管上述分析建立在kf/ks=500的條件下,但因為彈道輸運主要通過熱導率的尺寸效應來影響拓撲優化結果,所以改變kf/ks的值不影響體點導熱拓撲優化結果隨彈道效應強度的定性變化.定量上,體材料熱導率比的值越大,發生彈道輸運時不同尺寸結構等效熱導率的差異越大,相同努森數下彈道輸運對拓撲優化結果的影響越顯著.界面熱阻會使得材料間界面處出現溫度不連續,導致系統總熱阻增大,平均溫度升高[4].雙層材料間界面熱阻的影響會隨著材料尺寸的減小而增大[56],如果在拓撲優化中考慮界面熱阻,為了降低界面熱阻對導熱的阻礙作用,優化結果會朝著增大結構尺寸的方向發展.圖5中隨著彈道效應的增強,填充材料構型也明顯表現出粗壯結構增多、微小結構減少的趨勢,這表明雖然現在的優化模型未考慮界面熱阻,但所得的結果有利于抑制界面熱阻的作用.

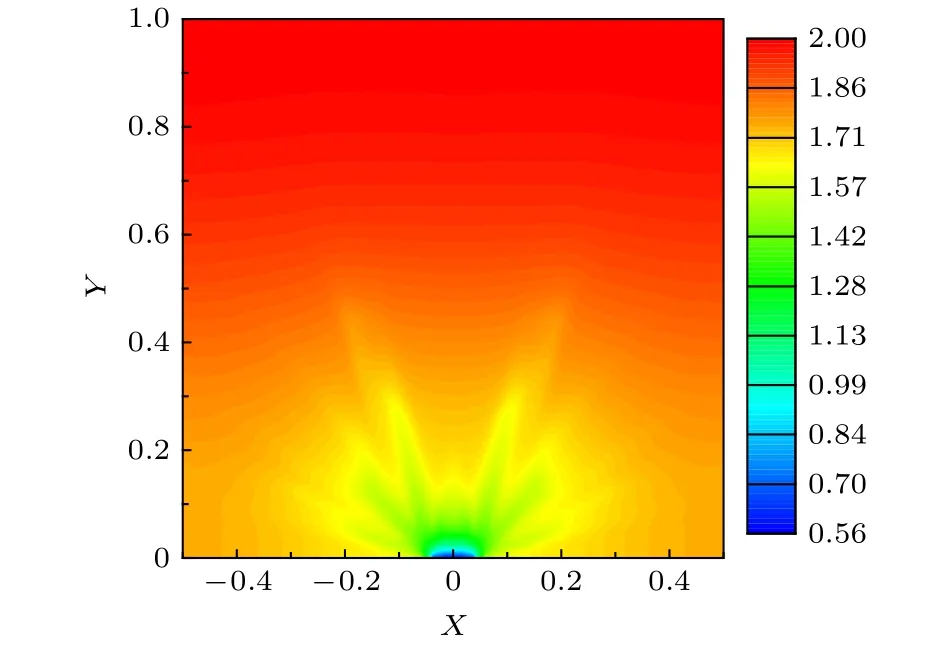
圖6 擴散導熱下插值 k-1 的拓撲優化所得的材料分布在 Kn=0.1 時的溫度分布Fig.6.The temperature distribution for the material distribution obtained by topology optimization which interpolates k-1in diffusive heat conduction at Kn=0.1.

4 結 論

針對微納米電子器件的散熱優化設計,結合聲子玻爾茲曼方程和固體各向同性材料懲罰方法,發展了適用于微納尺度下彈道-擴散導熱的拓撲優化方法.聲子玻爾茲曼方程被轉化為聲子輻射輸運方程,然后用離散坐標法求解以獲得某個設計方案下的溫度場; 拓撲優化則通過對聲子平均自由程的倒數進行插值的固體各向同性材料懲罰方法來實現,并采用對相對密度變量全局梯度施加顯示約束的方法來確保解的適定性和網格無關性.

成功實現了體點導熱問題在彈道-擴散導熱機制下的拓撲優化解,發現彈道-擴散導熱機制下,拓撲優化預測的最佳材料分布明顯不同于傅里葉定律下經典的樹狀結構,且會隨努森數Kn的變化而變化,表明微納米尺度下的導熱優化問題必須要考慮聲子彈道輸運的影響.在Kn較小時,解聲子玻爾茲曼方程的拓撲優化的結果會趨向傅里葉定律下于對熱導率倒數進行插值的拓撲優化結果,而非傳統的插值熱導率所對應的樹狀結構.隨著Kn的增大,拓撲優化結果中填充材料逐漸向低溫邊界附近聚集,其構型中粗壯的主干結構所占比例增大,微小的枝結構所占的比例降低,且優化后系統平均溫度和優化前系統平均溫度的比值增大.

拓撲優化結果和Kn的相關性與聲子彈道輸運產生的熱導率尺寸效應有關.擴散導熱機制下,不同尺寸的填充材料熱導率相同,均能有效構建高導熱通道; 但隨著彈道效應的增強,尺寸效應使得材料分布中微小結構的等熱導率比粗壯結構低,微小結構在提升系統導熱性能方面的作用不如粗壯結構,因而拓撲優化會向增多粗壯結構、減少微小結構的方向發展.當彈道效應足夠強時,填充材料會聚集在低溫邊界附近,主干和枝合并,呈團狀分布.