基于Lipschitz條件的一類非線性時滯廣義系統觀測器的設計
孫延修,黎虹,潘斌
(1.沈陽工學院基礎課部,遼寧 撫順 113122;2.遼寧石油化工大學理學院,遼寧 撫順 113122)
1 引言
系統的觀測器設計是控制領域研究的熱點,針對非線性系統觀測器的研究,近幾十年取得了很多的成果,但大多是針對未帶時滯的系統觀測器的設計[1-4].在社會生活生產的各個方面,如:冶金、網絡控制、通信、化工和機械傳輸等領域時滯現象廣泛存在,所以研究時滯系統更具實際應用意義[5-9].文獻[4]針對含有Lipschitz非線性項系統的狀態不可測量,分別設計了全維和降維觀測器.文獻[8]針對非線性項滿足Lipschitz條件的時滯系統的觀測器進行了設計,并對觀測器進行了H∞技術性能分析.文獻[10]針對一類非線性系統分別設計出了全維、降維觀測器,并給出觀測器存在的充分條件,通過利用線性矩陣不等式(LMI)求解出了觀測器的增益矩陣.文獻 [11]針對滿足Lipschitz條件的非線性時滯系統分別設計出了全維和降維觀測器,并通過對模型的仿真分析證實了觀測器設計方法的可行性.文獻[12]給出了具有時滯的Lipschitz非線性系統觀測器存在的充分條件,并設計出具有擾動的時滯Lipschitz非線性離散系統的魯棒觀測器.
廣義系統是一類形式更為一般化的系統,其在電力系統、電子網絡、機器人系統、經濟等領域有著廣泛的應用.隨著奇異系統理論的發展,針對廣義系統觀測器的設計及觀測器在故障診斷中的應用具有一定的積極意義[13-15].文獻[16]針對一類離散廣義時滯系統,通過系統變換結合系統差分方程的特點及范數的性質,給出了狀態觀測器存在的充分條件.文獻[17]針對一類時滯廣義系統的全維與降維觀測器進行了設計,并給出了觀測器增益矩陣的求解方法.文獻[18]針對一類時滯Lipschitz非線性離散廣義系統,分兩種情況對系統進行討論進而設計出觀測器,并給出了相應觀測器存在的充分條件.
目前,針對非線性時滯廣義系統觀測器的設計與研究成果較少.本文針對一類含有Lipschitz非線性項的連續時滯廣義系統的觀測器進行了設計,利用Schur補引理給出了系統觀測器存在的充分條件,最后利用數值算例驗證了觀測器設計方法的可行性.
2 問題描述
考慮如下非線性時滯廣義系統:

其中,E∈Rn×n為奇異矩陣且滿足rank(E)=q 為常數矩陣,u(t)∈Rm,y(t)∈Rp分別是系統的輸入和輸出. 假設 1系統的非線性項Φ(x(t),x(t?d),u(t)),滿足Lipschitz條件,即有 其中,LΦ為大于0的Lipschitz常數. (I)當系統的非線性項等于零時,根據假設2系統(1)可轉化為: 進行線性變換z(t)=x(t)?Ny(t),則可以去掉(t)項得 設計如下狀態觀測器: 令e(t)=z(t)?(t),由觀測器(3)與系統(2)使得到的誤差系統(4)漸進穩定: (II)當系統存在滿足Lipschitz條件的非線性項時,根據假設2系統(1)轉化為: 進行線性變換z(t)=x(t)?Ny(t),去掉(t)項式后為 其中,Φ(x(t),x(t?d),u(t))= Φ′(z(t),z(t?d),u(t)). 假設 3系統 (1)經線性變換后得到 (5)式中的非線性項 Φ′(z(t),z(t?d),u(t)),滿足Lipschitz條件,即有 其中,LΦ′為大于0的Lipschitz常數.根據假設3設計如下狀態觀測器: 令e(t)=z(t)?(t),由觀測器(6)與系統(5)使得到的狀態估計誤差系統(7)漸進穩定: 利用線性矩陣不等式(LMI)的方法,考慮時滯廣義系統的觀測器設計及狀態估計誤差系統的穩定性問題,得到兩個觀測器存在的充分條件. 定理 3.1若存在對稱正定矩陣P,Q和增益矩陣L,Ld滿足下列不等式(8),則(3)式為系統(2)的觀測器: 矩陣M1<0等價于定理中的矩陣不等式(8),故?V<0誤差系統漸進穩定,定理得證. 定理 3.2若存在對稱正定矩陣P,Q和增益矩陣L,Ld滿足下列不等式(9),則(6)式為系統(5)的觀測器: 其中,P,Q為對稱正定矩陣,X=PT,=PL,d=PLd,α=∥T∥LΦ′為大于零的實數,?表示對稱矩陣中的對稱部分. 證明設e(t)=z(t)?(t),則由(5)式和(6)式可得誤差系統的狀態方程為 根據Schur補引理,矩陣M2<0等價于定理中的矩陣不等式(9),故?V<0誤差系統漸進穩定,定理得證. 注 3.1定理3.1,定理3.2中選取了相同的李雅普諾夫函數,定理3.2考慮到系統含有的Lipschitz非線性項,為了易于求取增益矩陣L,Ld,根據schur補引理將矩陣不等式M2<0變換成與(9)式等價的形式,給出了含有Lipschitz非線性項時滯系統觀測器存在的充分條件. 例 4.1考慮時滯廣義系統(1)的參數如下: 系統(1)可以轉化為(5)式的形式,根據文獻[11]中針對增益矩陣的求解方法,利用線性矩陣不等式可以計算得出含Lipschitz非線性項時滯廣義系統觀測器的增益矩陣: 主要研究了一類含有Lipschitz非線性項的時滯廣義系統的觀測器設計問題.考慮到廣義系統的特殊結構,基于時滯系統觀測器的設計方法和線性矩陣不等式的方法,設計出了含Lipschitz非線性項條件下的一類時滯廣義系統的狀態觀測器,并根據Schur補引理給出了時滯系統觀測器存在的充分條件和時滯系統觀測器增益矩陣的求解方法.最后,通過結合文獻[11]中的數值算例驗證了含Lipschitz非線性時滯廣義系統觀測器設計方法的有效性.關于含有非線性項的不確定廣義時滯系統觀測器的設計則可作為進一步的研究方向.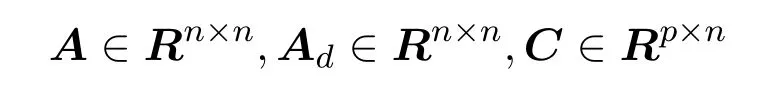

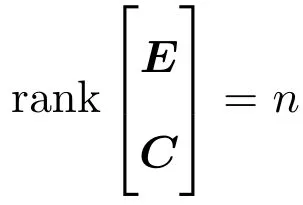
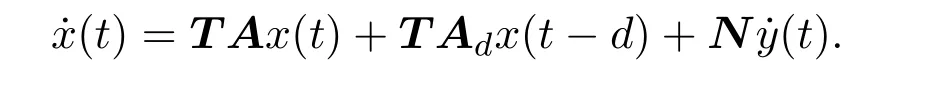
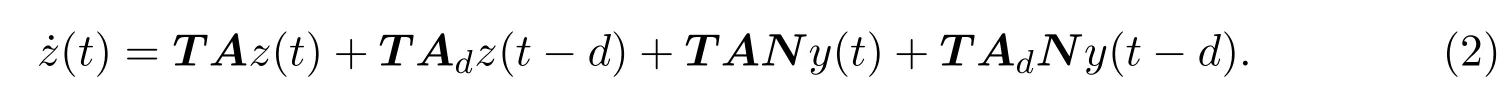
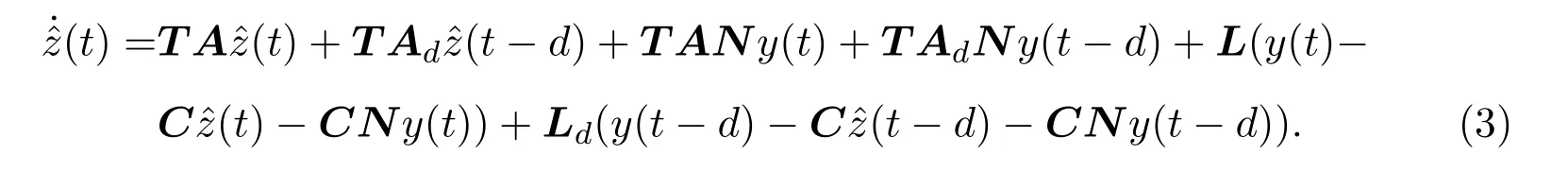

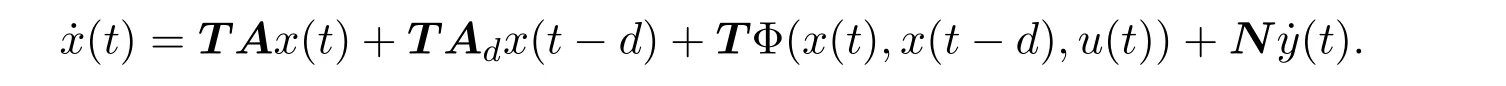



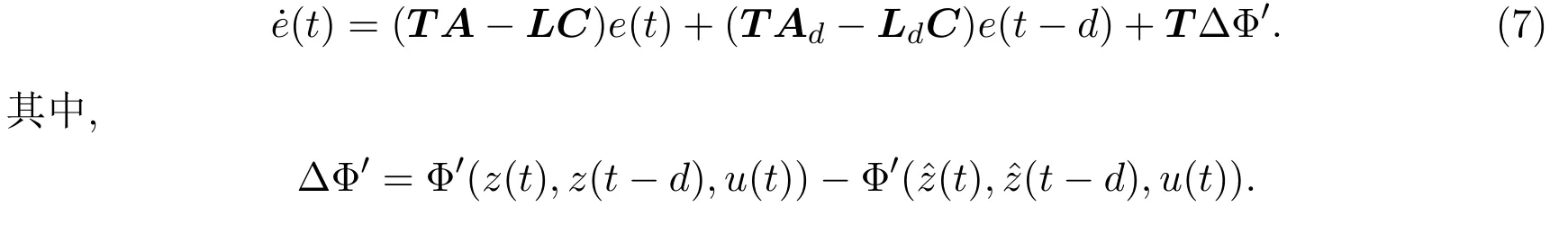
3 主要結果

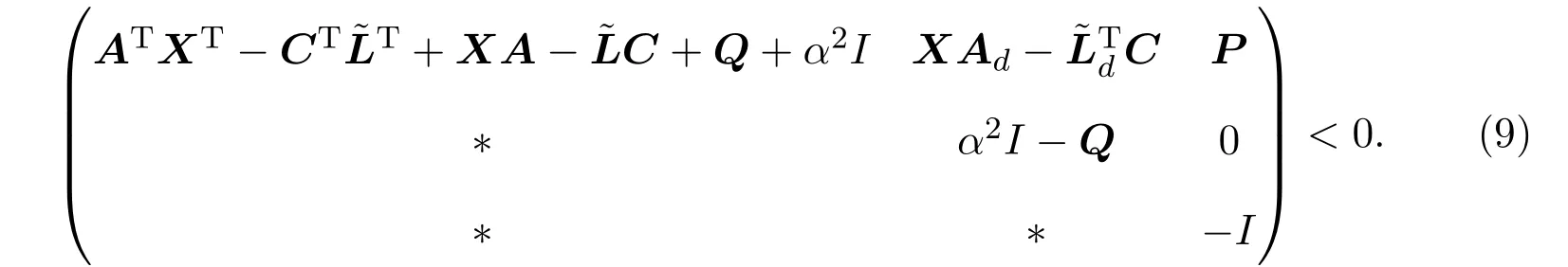

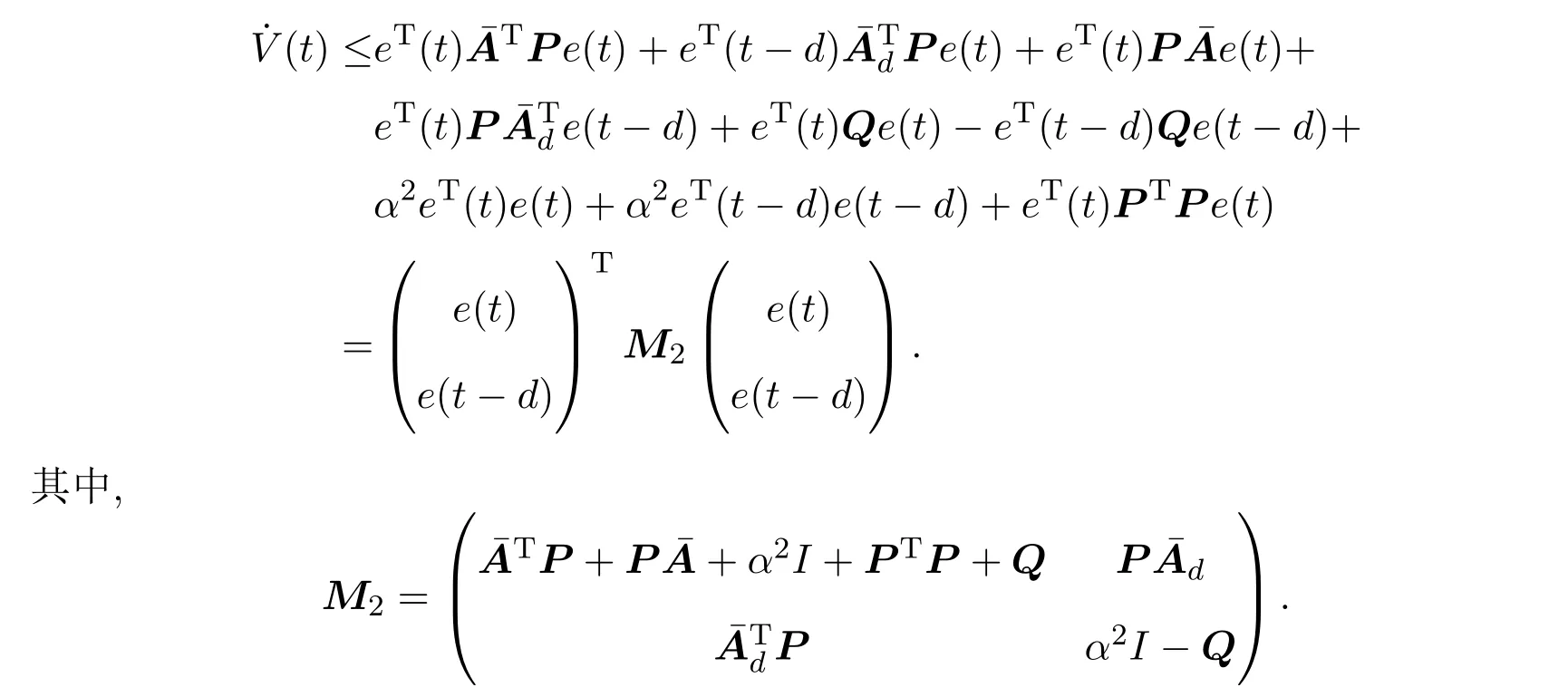
4 數值算例
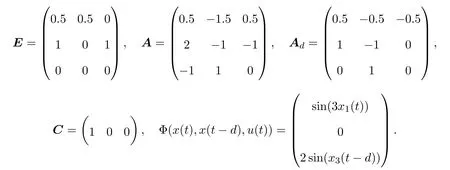
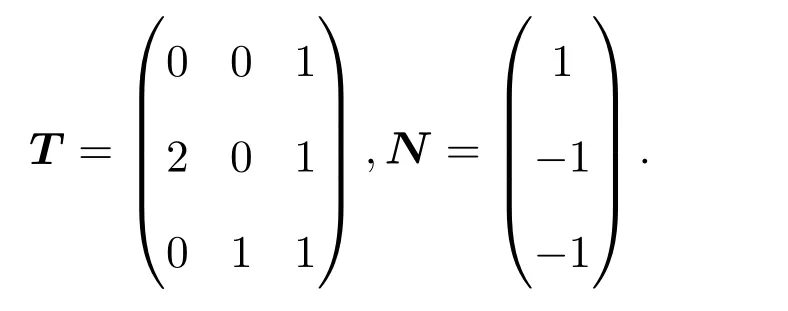
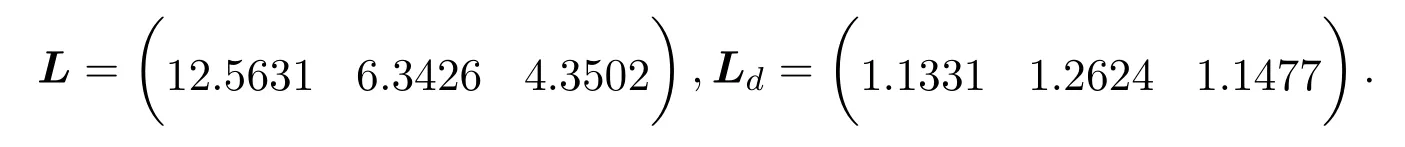
5 結論

