三維地形頻率域井筒電磁場區域積分方程法模擬*

李靜和 何展翔 孟淑君 楊俊 李文杰 廖小倩

1)(桂林理工大學地球科學學院,桂林 541004)

2)(南方科技大學地球與空間科學系,深圳 518055)

井筒電磁法作為一種高效的地球物理勘探技術特別適合我國地形復雜地區(沙漠、高山等)的油氣資源勘探.地形起伏區域對井筒電磁響應的觀測具有嚴重影響,但到目前為止人們對三維井筒電磁地形效應特征的研究十分有限.本文提出基于區域劃分的積分方程法模擬帶地形頻率域井筒電磁系統響應,與基于偏微分方程的有限差分、有限單元法相比,該方法能更高效地模擬地形響應.首先根據地形起伏情況定義感應數,將地形條件下目標體的井筒電磁場模擬區域劃分為參考模型、背景介質及目標體介質分布子區域,針對各子區域的模擬計算特點,配置Anderson算法、穩定型雙共軛梯度-快速傅里葉積分方程算法,從而獲得三維地形頻率域井筒電磁場響應.通過將計算結果與半空間模型的Anderson算法解析解、帶山谷地形模型的其他已發表的三維邊界積分方程結果進行對比,檢驗了本文算法的精度及高效性.最后,系統分析了山谷地形對井筒電磁地井觀測系統電磁場響應的影響特征.本文研究結果對三維井筒電磁地形效應的識別和校正具有指導意義.

1 前 言

我國油氣資源短缺已經成為國民經濟發展的瓶頸,但現有油氣儲量的采收率仍然不高,大量剩余油氣資源難以發現和采出.發展地球物理新技術對于剩余油氣儲層的發現、油氣動態開采過程的監測及采收率的提高具有重要意義.與常規的重力法、磁法及地震法等方法相比,電磁法由于在探測油氣介質時電阻率、極化率等參數變化相對波速、密度等參數更敏感,而成為油氣儲層探測最重要的手段之一.對地面電磁勘探方法而言,發射源和接收器均布置于地面之上,地表電磁噪聲及圍巖介質的濾波作用,使得地面電磁接收數據的信噪比較低.隨著研究的深入,油氣儲層電磁探測研究的方向逐漸轉入地下[1].井筒電磁法的獨特優點在于將接收或發射裝置或者二者均放置于井中特定深度,因而對于井中發射而言,可對目標層位形成最直接的激發; 而對于井中接收來說,由于井中電磁噪音平靜,所以目標體異常信號幾乎不被背景介質濾波衰減,從而具有較高信噪比[2].

在復雜介質(如起伏地形)電磁場正演模擬方法中,基于非結構化網格、無網格及自適應網格有限元法開展的數值模擬研究是當前的主流[3-4],采用有限差分法[5]及派生的有限體積法[6]開展復雜介質電磁場模擬的研究亦不斷涌現.微分方程法模擬復雜介質的、電磁響應需謹慎處理邊界截斷、誤差積累、場源奇異性等問題.對帶金屬套管的地井電磁模擬而言,微分方程法還需特別解決包含井孔在內的特殊邊界和網格剖分問題,這在當前仍屬于一項艱巨的任務[7,8].而積分方程法模擬僅需要局部空間離散,求解精度高,相較于微分方程法無需考慮金屬井孔電磁模擬問題,在三維井筒電磁場模擬中,這一優勢更為明顯[9-13].

盡管積分方程法在涉及井筒的大尺度電磁場模擬過程中比微分方程有優勢,但數值求解積分方程比求解微分方程需處理更為困難的數學問題.針對電性多面體問題,Tiberi等[13]提出解析微分特征基函數的譜域積分方程法,Nie等[14]采用預校正的快速傅里葉變換法開展隨鉆測井電磁場模擬,Chobanyan等[15]提出雙高階大范圍的廣義體-面積分方程法.目前,國內外開展積分方程法模擬帶地形頻率域電磁場響應的研究工作還很少見.針對二維地電模型模擬問題,國內外學者多數采用矩形單元及不同階數的積分方程法開展數值模擬,對復雜模型的剖分通常采用加密網格方法以獲取高精度數值模擬結果.但矩形單元很難精確模擬復雜地形和復雜地下目標體,而加密網格則導致計算量及存儲量增大[16].

為此,Zhdanov等[17]提出基于分離模擬技術的體積分方程法,嘗試高效地解決同時存在三維大尺度鹽丘體與二維大尺度薄層目標體的電磁場模擬問題,但其采用規則六面體網格剖分且未考慮地形起伏問題,模擬的目標體也僅局限于規則形體.有限元模擬中廣泛采用的非線性結構、自適應四面體網格及自適應矩形網格,可有效模擬復雜地形及地下目標體,其理論發展與實際應用已漸趨成熟,但涉及較大計算量及存儲量[18].積分方程區域分解是另外一種提高模擬井筒電磁多尺度目標能力的方法,其在工程、通訊領域電磁模擬方面具有較好的應用,但由于要求每個子區域具有相同的大小和結構,使得對井筒電磁非周期或者復雜目標的電磁建模有一定的局限性[19].

綜上所述,盡管電磁法的數值模擬理論及算法已取得了長足發展,但對于多源多頻率井筒電磁法,利用高效高精度正演模擬技術,研究地形響應對井筒電磁場異常的影響規律和提出相應的校正方法,仍是當前該方法走向實用化亟待解決的兩個重要方面.本文基于深井井旁目標體二次電磁場響應與地形響應弱耦合的前提,引入區域分解理論對研究區域采用分離模擬技術,結合高斯濾波半解析算法,開展區域體積分方程法研究,實現起伏地形和復雜儲層的頻率域井筒電磁響應的高效、高精度模擬,并利用多方位Walkaround觀測系統實現三維頻率域地井電磁正演模擬算例分析,為推進該方法的實用化提供了技術基礎.

2 方法理論

2.1 積分方程

理論上積分方程模擬電磁場求解的過程為: 在電性參數有別于背景介質的異常區域的網格剖分基礎上,推導滿足勘探問題的可控源電磁三維體積分方程,采用穩定型雙共軛梯度法求解目標區域離散化后的大型線性方程組.三維積分方程正演模擬問題的實質為均勻半空間介質或水平層狀背景介質中異常區域的三維地面可控源電磁場模擬問題的轉化.即擬采用地面發射源激發一次場,在電磁場遠區定義范圍之外面積性觀測異常電磁場.

考慮多方位Walkaround地井電磁觀測系統(圖1),第n層的節點處總電場可表示為該點入射場與散射場之和[11]:

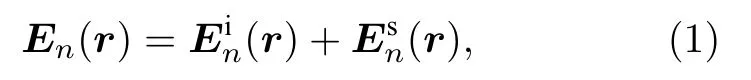
其中 En(r)為 總電場,為層狀介質中入射場,為 異常體散射場;為三維空間位置.由感應電流引起的散射場為

圖1 積分方程模擬三維地井電磁場觀測系統示意圖(未顯示地形)Fig.1.Sketch of 3D (three-dimensional)SBEM (surface to borehole electromagnetic)measurement system using IE(integral equation)without topography.

注意到,求解格林函數過程涉及巨大的計算量及存儲量,本文將正演過程中的并矢格林函數分解,結合積分方程核,運用快速傅里葉變換 (FFT)加速計算.將整體研究區域網格剖分,離散體積分方程為矩陣方程組,結合穩定型雙共軛梯度法求解方程; 層狀背景介質電導率只在z方向變化,對積分核中的電場并矢格林函數做如下處理:

2.2 區域劃分

電磁場響應的數值模擬方法可應用于實際工程問題,但往往涉及求解大型矩陣方程組.對應的計算區域往往是多尺度且其形態可能很不規則,如三維地形、巨型鹽丘與局部異常目標體,會給模擬計算帶來很大的困難.此外,值得注意的是,針對網格剖分尺度,數值方法對長波現象具有較好模擬精度.若為了提高分辨率而加密網格剖分密度,亟待解決的問題將是求解過程的計算量和速度的限制.本文將區域分解理論引入多尺度電磁場響應的積分方程模擬問題,即引入參考模型,將三維地形、巨型鹽丘與局部異常目標體等視為不同子區域,子區域應盡可能規則,從而將原問題的求解轉化為在多個子域上的求解.由于上述操作有別于精確定義的區域分解方法,故稱之為“區域劃分”.對于區域劃分原則,本文采用感應數作為區域劃分的標準.

假定地形起伏的劇烈程度為 Lp(定義為研究區域最大高程變化與水平距離的比值),感應幾何尺寸由趨膚深度度量:

式中Re為取實部,kp為波數,根據電磁散射理論,感應數可以表示為

目前對大、小感應數的界定并無定論,本文取Mp?1為小感應數,相反為大感應數.

以井筒電磁地井觀測系統為例,針對大尺度電磁場模擬問題(圖2(a)),大感應數情況下,地下深處異常體對地形的影響忽略不計,先設置參考背景模型,求解純地形(缺失油氣儲層目標體的情況)引起的頻率域地井電磁場響應,將其作為新的背景一次場,再求解油氣儲層目標體異常響應.對于小尺度電磁場模擬問題(圖2(b)),在小感應數情況下,地形和地下深處異常體之間的電磁場相互耦合很小,可以忽略,可以將地形與地下油氣儲層目標體作為統一“目標體區域”,先求解參考背景模型一次場,再求解這一“目標體區域”引起的綜合電磁場響應.通過采用上述場“劃分”模擬,實現考慮起伏地形、復雜油氣儲層目標體三維頻率域地井電磁場的快速正演模擬.

圖2 區域劃分示意圖(剖面圖)Fig.2.Sketch of domain decomposition in profile.

2.3 區域積分方程模擬

考慮包含目標異常體在內的整個研究區域(目標剖分區域D),采用三維多方位地井電磁觀測系統,如圖3(a)所示,研究范圍內具有三維地形、不規則起伏層狀背景介質及油氣目標體分布.按區域劃分步驟,引入參考模型,如圖3(b)所示,電導率為 σh,可設置為均勻半空間介質或層狀介質; 假設不規則起伏層狀背景介質與三維地形之間滿足區域劃分標準的小感應數范疇,將上述二者劃分為復雜地質構造背景介質 σb(圖3(c)); 假設三維地形、不規則起伏層狀背景介質內油氣目標體滿足區域劃分標準的大感應數范疇,則可將三維地形、不規則起伏層狀背景介質電磁響應作為求解油氣目標體 σ 的電磁場響應的入射場(圖3(d)).

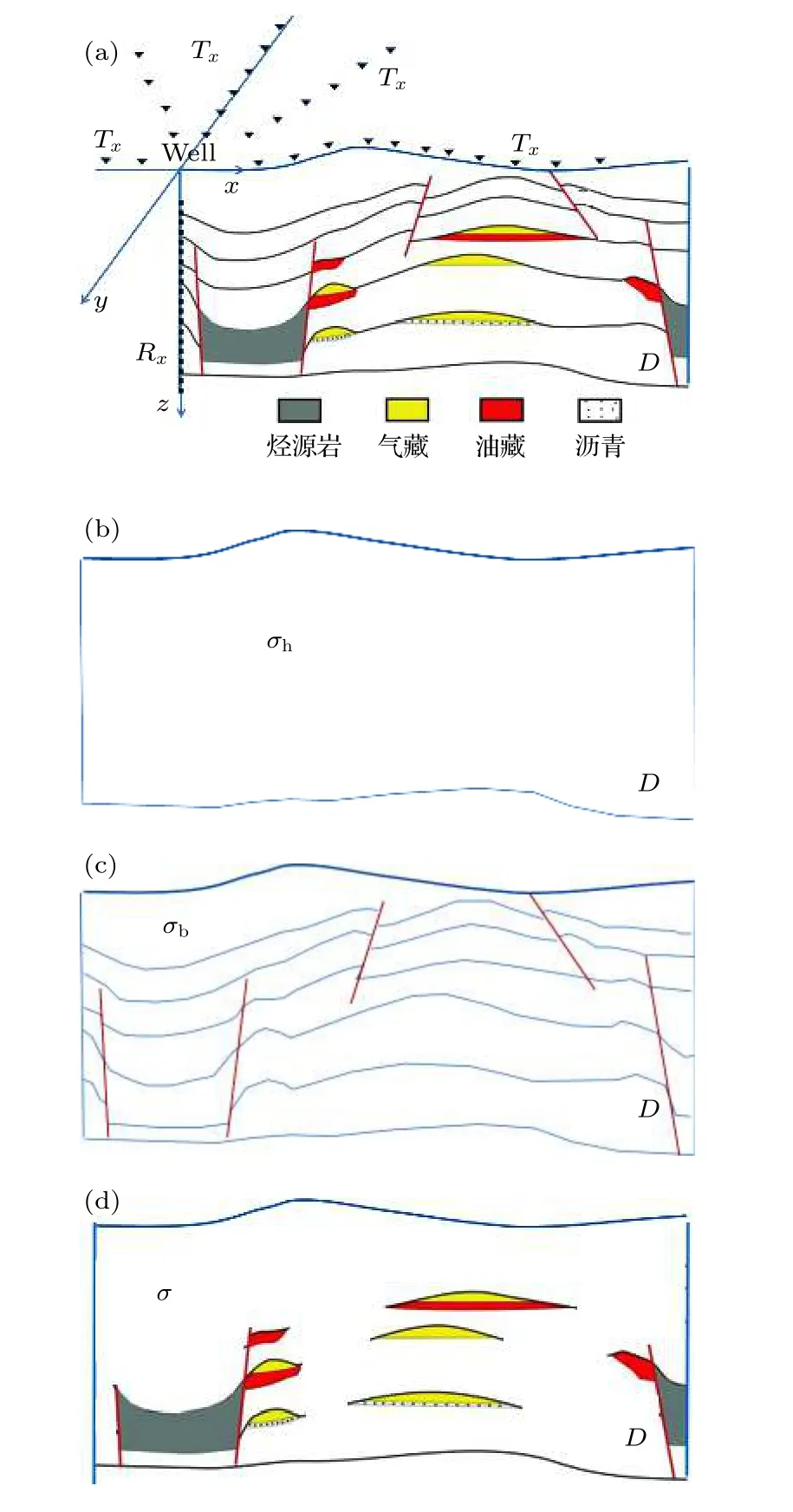
圖3 觀測系統及計算區域劃分示意圖 (a)三維地井電磁; (b)參考空間介質; (c)復雜地質構造背景介質; (d)油氣目標體Fig.3.Sketch of domain decomposition and observation system: (a)3D SBEM; (b)reference model; (c)background model; (d)oil and gas model.

求解過程的對比度函數可表述為

其中 σ 及 σb為油氣目標及復雜地質構造的背景層介質的電導率; 當 σb等于 σh時,表示不存在三維地形、不規則起伏層狀背景介質,為傳統積分方程模擬; 當 σb有別于 σh時,則表示考慮三維地形、不規則起伏的層狀背景介質,采用區域積分模擬.

對于如圖3(b)所示的參考模型介質,其電磁場響應作為求解圖3(c)所示區域劃分的異常電磁場響應的積分方程的入射場,采用(1)式的三維積分方程求解過程耗費機時,尤其是當解決多場源、多頻率地井電磁場響應時,其計算復雜度隨場源數和頻率數乘積倍增.Anderson算法采用濾波算子,可提供多層層狀介質在任意方向電偶極子和磁偶極子激勵下的電磁響應[21].此時,定義入射場響應為,因而三維地形與不規則起伏層狀背景介質之間滿足區域劃分標準的小感應數范疇的三維電場 Eb(r)的體積分方程為

假設如圖3(d)所示子區域滿足大感應數范疇,則由 (9)式可獲取三維地形與不規則起伏層狀背景介質作為入射場的電場響應 Eb(r),則三維地形、不規則起伏層狀背景介質內油氣目標體的電場響應的體積分方程表示為

式中 r ∈/D 且為井孔中接收點空間位置,k2特指如圖3(d)所示子區域滿足大感應數范疇的波數.再次利用穩定型雙共軛梯度法求解,即可獲得由圖3(c)所示計算區域引起、井孔內任一點接收的電場.井孔內任一接收點的磁場響應則通過地井電磁滿足的磁場積分方程,根據上述電場積分方程的推導過程求解獲取,在此不再贅述.

至此,三維地形條件下、不規則起伏層狀背景介質內油氣目標體勘探電磁場響應的模擬問題轉化為區域劃分的三個子區域的電磁場模擬問題,其中,參考模型子區域采用高斯濾波算子快速提供純均勻空間或水平層狀空間背景介質的入射場; 三維地形與不規則起伏層狀背景介質的綜合電磁響應、純油氣目標體的電磁響應則通過采用穩定型雙共軛梯度法-快速傅里葉變換求解體積分方程快速獲取,由此實現區域積分方程的三維地井電磁響應模擬.

3 算 例

3.1 算法驗證

為了驗證所采用的積分方程法(3D IE)三維數值模擬的有效性,將本文模擬結果與阮百堯等[22]使用邊界積分方法(3D BIE)計算三維起伏地形頻率域電磁響應的結果、Anderson濾波算法計算層狀介質電磁響應的結果進行對比分析.綜合前人發表的研究成果,采用均勻半空間介質地電結構模型,導電率為0.01 S/m; 考慮放置于地面的垂直磁偶極源,場源位于坐標系原點,激發頻率為1000 Hz,單位電流強度供電; 若干接收點位于x軸方向主剖面(過場源點剖面)上,點距為非均勻間距,從靠近場源到遠離場源采用的網格間距分別為1,3,7,10,30 m,未考慮地形影響.理論上,場源及觀測系統為三維,電性結構是一維的,水平磁場分量可通過三維邊界積分方法、Anderson算法及三維積分方程方法模擬計算.由磁偶極源在均勻空間介質引起的歸一化水平磁場分量如圖4所示.模擬結果表明,阮百堯等提出的邊界積分方法、Anderson算法正演計算結果與此模型的三維積分方程模擬數值結果一致,水平磁場分量隨接收點離場源距離增大而逐漸衰減,三種模擬數據間擬合誤差小于1%,從而達到檢驗本文三維數值模擬算法的可行性及有效性.

計算效率方面,針對上述驗證模型,在PC 12 G RAM和雙 i5 CPU環境下,Anderson 算法采用半解析算法模擬計算,具有高效的三維電磁場運算能力,總耗時為0.1 s; 三維邊界積分方程法模擬區域網格剖分數為30 × 30,另需包含各邊界20個網格作為截斷邊界,因而總體網格數量需求較大,計算耗時123 s; 本文引入快速算法及區域積分方程模擬算法,區域剖分網格數量為20 × 20 × 20,積分方程三維正演算法總耗時86 s,傳統積分方程法[11](矩量法)總耗時957 s (表1).可見,引入快速算法及區域劃分策略后,本文區域積分方程三維正演模擬針對包含空氣在內的整體區域剖分的計算效率較矩量法提高顯著,與三維邊界積分計算效率相比也有較好的效果,但相比Anderson 算法在提供三維均勻介質或層狀介質的一次場方面的高效特征而言,后者更具高效性,為后續將Anderson 算法融入區域積分方程法來模擬以提高計算效率奠定了基礎.

圖4 均勻半空間模型三維積分方程法(3D IE)、三維邊界積分法(3D BIE)、Anderson算法模擬結果對比圖Fig.4.Magnetic field of reference model calculated by 3D IE,3D BIE and Anderson code.

表1 均勻半空間介質地電結構模型的不同算法的電磁場模擬效率對比Table 1.Comparison of computational effectiveness of modeling electromagnetic field via different algorithms for a half homogeneous medium.

3.2 三維地形響應模擬驗證

由于三維起伏地形頻率域的地井電磁場響應的模擬結果發表的較少,本文將三維積分方程法的模擬算法用于三維起伏地形頻率域地面電磁場響應的模擬計算,并與三維邊界積分的模擬結果對比.如圖5所示,收發裝置采用地面電磁觀測系統,垂直磁偶源位于山谷地形底部,激發頻率為1000 Hz;接收點位于y=0剖面,點距為非均勻間距; 地下半空間介質導電率為0.01 S/m.三維山谷地形為倒梯形體,上頂面為200 m × 200 m,下底面為40 m × 40 m,縱向高差為50 m.采用本文提出的區域劃分方法,將上述含山谷地形的模擬算例劃分為層狀介質參考模型(圖3(b)),即包含空氣層和地下電導率為0.01 S/m的介質層; 將山谷地形作為區域劃分異常目標體(圖3(c)).于是,在參考模型中對比度函數為零,而包含空氣層的山谷地形目標區域的對比度為1,需要求解的區域介質與參考模型介質在對比度函數上具有顯著的差異,保障了積分方程模擬的精度.

圖5 三維山谷地形及地面電磁觀測系統示意圖,Tx為場源位置,Rx為接收點位置Fig.5.Sketch of 3D valley terrain with surface electromagnetic.Tx denotes transmitter and Rx is receiver.

首先采用Anderson算法求解參考模型分布在y=0剖面上各接收點的一次場響應,將一次場響應作為(9)式右端項入射場,采用穩定型雙共軛梯度-快速傅里葉變換算法求解積分方程組,即可獲取三維地形電磁場響應.三維邊界積分方程模擬將地形問題轉化為空氣空間及介質空間的矢量面積分問題,簡化了三維邊界積分求解過程; 針對地形區域采用加密三角單元積分(相應計算量增大),并將地形影響視為常數項因(地形響應模擬精度有限).圖6所示為三維山谷地形的三維積分方程模擬、三維邊界積分模擬地面水平磁場分量的歸一化響應及二者模擬地形響應差值的對比情況.如圖6(a)和圖6(b)所示,兩組磁場分量模擬結果的衰減變化趨勢一致性較好,地形起伏區域(x軸—100——40 m,40—100 m)在相應磁場響應曲線上均有所反映,表明了本文區域積分方程模擬起伏地形的可行性.基于上述兩種算法模擬地形響應精度不同的問題,繪制了三維區域積分方程算法相對三維邊界積分方程模擬地形水平磁場響應的差值曲線(圖6(c)和圖6(d)).差值曲線表明,相對三維邊界積分方程算法,本文提出的區域積分方程算法模擬地形響應的幅值最小值達7% (Hy分量),最大值達20% (Hx分量),驗證了本文正演模擬方法的有效性.

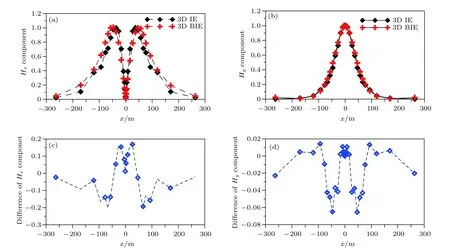
圖6 三維山谷地形三維積分方程模擬、三維邊界積分模擬地面磁場分量歸一化響應及其差值對比圖Fig.6.Magnetic field of 3D valley terrain calculated by 3D IE and 3D BIE: (a),(b)Total magnetic field; (c),(d)difference of magnetic field between IE and BIE.

3.3 多方位地井電磁算例

為分析本文提出的區域積分方程方法在地井電磁觀測系統上模擬的可行性,設計均勻半空間層狀介質模型,導電率為0.01 S/m; 垂直電偶源位于地面,其水平位置與接收井口距離為100 m,激發頻率為1000 Hz; 接收井深度方向0—100 m內布置若干縱向電場分量接收點,間距為5 m.圖7所示三維區域積分方程方法(3D IE)與Anderson算法的模擬結果完全吻合,數據間擬合誤差小于1%,驗證了本文算法用于地井電磁場響應模擬計算的可行性,為后續將Anderson算法嵌入三維地形地井電磁多方位觀測的電磁場模擬降低計算代價奠定了基礎.

進一步,設計考慮三維地形條件下地井電磁多方位觀測方式的算例分析,探索地形對地井電磁場的影響規律.如圖8(a)所示,假設三維山谷地形三方位地井電磁觀測系統采用三方位水平徑向電偶源,分別為主剖面觀測(Tx1位于地形上升中段)、旁側觀測(Tx2位于地形旁側)及對側觀測(Tx3與地形在井孔的兩側); 為便于對比分析,各場源與接收井水平距離均為300 m,激發頻率為25 Hz.主剖面觀測場源位于山谷地形內,其余方位觀測場源位于地面,接收井0—100 m內布置若干縱向電場分量接收點,間距為5 m,如圖8(b)—(d)所示.

圖7 均勻半空間地井電磁觀測三維積分方程法、Anderson算法模擬電場響應對比Fig.7.Electric field of reference model calculated by 3D IE and Anderson code for 3D SBEM.

圖8 三維山谷地形及多方位地井電磁觀測示意圖Fig.8.Sketch of 3D valley terrain with multi-azimuth SBEM.

本文采用Anderson算法計算區域劃分參考模型的一次場響應,利用區域積分方程方法模擬計算上述地井電磁多方位電磁場響應.當場源與接收井孔之間存在地形空間時,在地形空間深度范圍內,場源與接收點的傳播空間受阻,在觀測總電場響應(黑色曲線)上體現為幅值低于散射場響應(紅色曲線)的畸變現象(圖9(a)).在場源、地形底部與接收井孔測點為連線區域,地形影響產生的上述畸變現象減弱,但引起顯著的高幅值異常,揭示了地形存在.當接收點深度大于地形深度范圍,地形影響基本無效,總電場、散射場響應趨于正常分布,并與Anderson算法提供的均勻空間電場響應曲線(藍色曲線)分布吻合.旁側觀測模擬結果如圖9(b)所示,由于地形與場源位置關于井孔位置為正交關系,地形深度范圍場源激發一次場占主導,但與地形底部深部的相同位置接收點仍受到上述畸變現象影響; 大于地形深度接收點電場的響應則受頻率域電磁法體積效應、旁側影響干擾,導致總場響應較Anderson算法提供的一次場響應的幅值增加.由于井孔位于地形與場源中間,對側觀測方式下地形引起的散射電場較微弱,如圖9(c)所示,總場響應與Anderson算法提供的一次場的響應基本一致,大于地形深度接收點電場的響應仍受體積效應、旁側影響干擾.

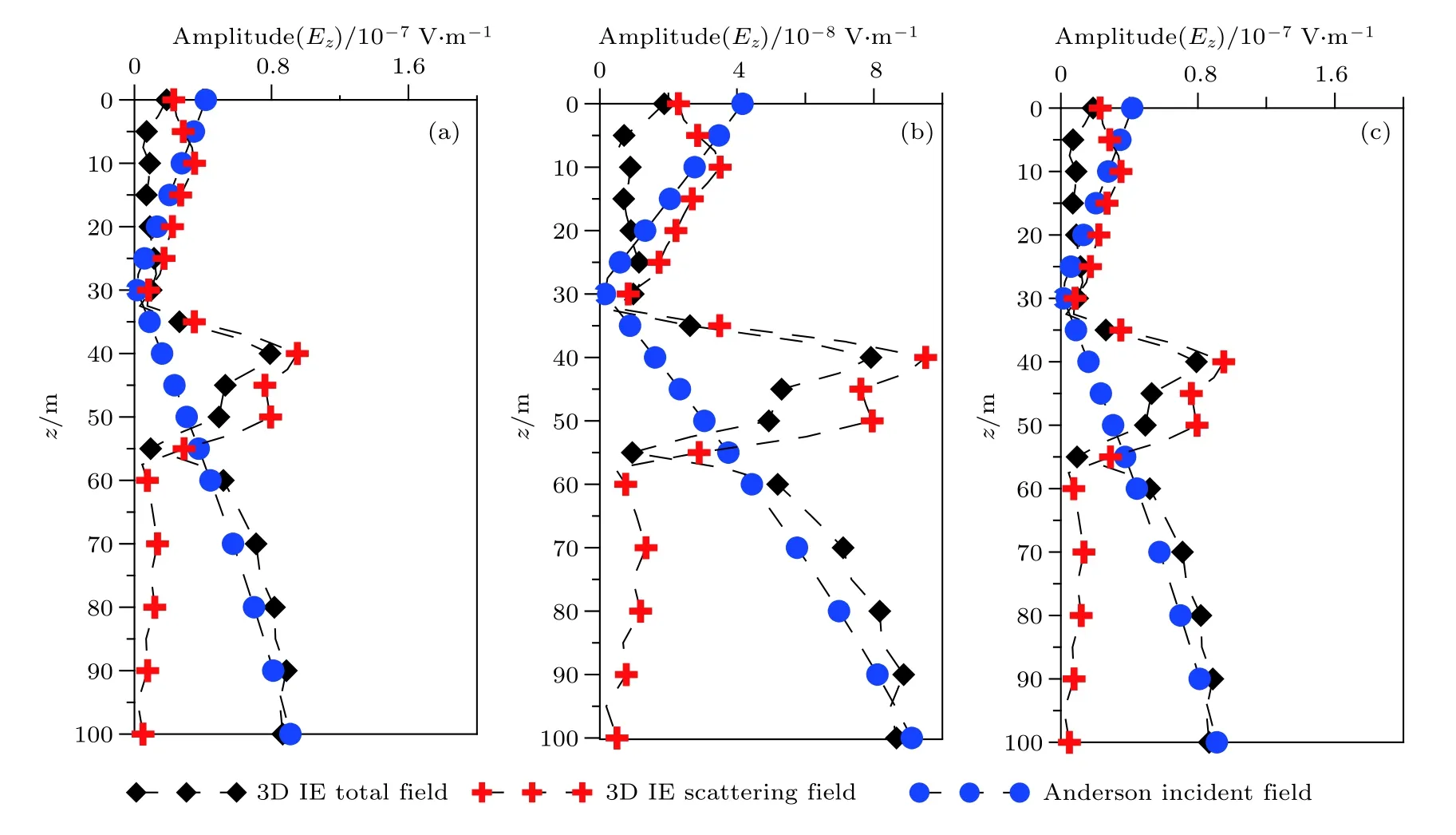
圖9 三維山谷地形三方位地井電磁場響應 (a)Tx1場源; (b)Tx2場源; (c)Tx3場源Fig.9.Electric field of 3D valley terrain with multi-azimuth SBEM: (a)Tx1; (b)Tx1; (c)Tx1.

綜上分析表明,當場源布設于地形內或者距離地形比較近時,地井電磁觀測響應將會受到嚴重影響,甚至出現電磁場幅值畸變現象,嚴重干擾手續數據解譯推斷; 不同方位場源位置激發條件下,地形對地井電磁響應的影響規律及幅值強度各異,場值受到頻域電磁勘探體積效應、旁側影響的干擾亦有所不同,該特征為有效識別三維地形影響及剔除相應地形影響提供了新的方法手段.

4 結 論

1)針對三維地形頻率域井筒電磁響應的高效模擬問題,引入區域劃分方法,將三維起伏地形條件下復雜背景介質及目標體電磁場響應的模擬區域劃分為參考模型、背景介質模型及目標體子區域,結合Anderson算法、穩定型雙共軛梯度-快速傅里葉變換算法,對不同劃分子區域采用不同算法進行高效模擬計算,開展了三維區域積分方程模擬算法的研究,解決了無需考慮增加地形剖分網格單元數量、截斷誤差累積及井筒特殊邊界處理等問題,而且通過積分方程模擬局部剖分特性、高效模擬特點,構建了適用于三維井筒電磁勘探地形響應的模擬算法.

2)基于Anderson算法及現有三維邊界積分方程的模擬算法理論,設計無地形均勻層狀介質模型、含山谷地形均勻層狀介質模型,采用地面場源、接收點布設觀測系統開展三維區域積分方程模擬算法的精確度及計算效率的分析.研究表明: 三維區域積分方程模擬算法具有與解析解求解的Anderson算法相當的計算精度,而Anderson算法在提供三維均勻層狀介質一次場響應方面具有較高的計算效率,因而可融入三維區域積分方程模擬算法以降低計算成本; 地形響應模擬方面,三維區域積分方程模擬算法較三維邊界積分方程具有更高的模擬精度及計算效率.

3)考慮山谷地形的三維地井電磁多方位電磁勘探系統,采用三維區域積分方程算法模擬場源位于主剖面、旁側剖面及對側剖面總電場及散射電場響應.通過與Anderson算法提供無地形均勻層狀介質的一次場響應對比分析表明: 三維地形場值響應對地井觀測場值影響較大,甚至出現誤導后續數據推斷解譯的畸變現象; 地形、場源與井孔位置差異導致地形響應規律特征不同,結合多方位地井電磁觀測系統布設,可有效甄別地形影響的存在性及干擾程度,為高精度、高效剔除地形響應影響奠定了理論基礎.